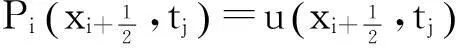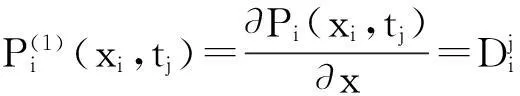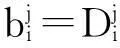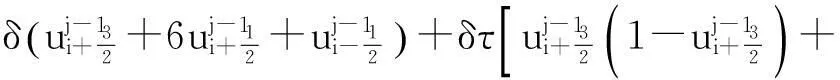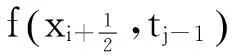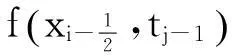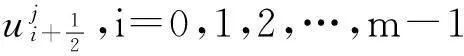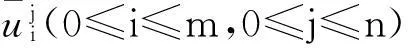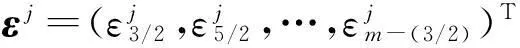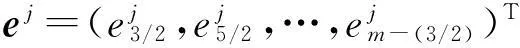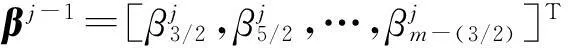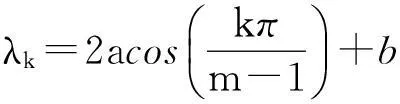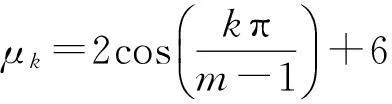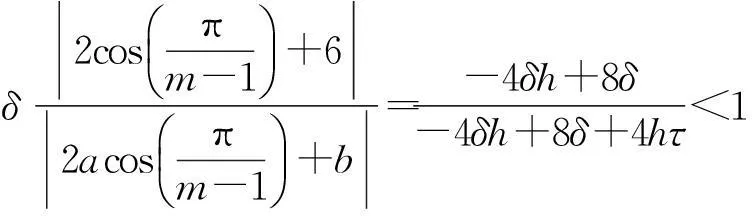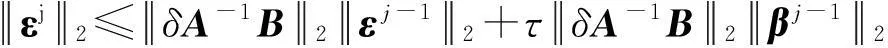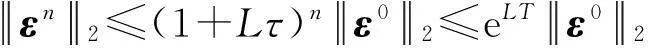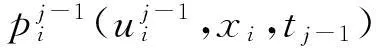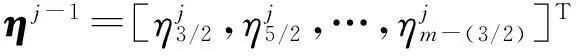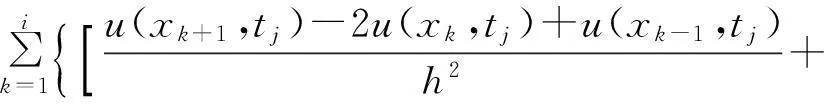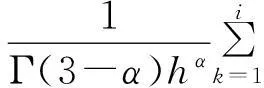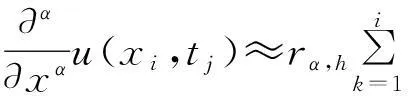非线性空间分数阶Fisher方程的数值解法

陈雪娟,陈景华

(集美大学理学院,福建厦门361021)

非线性空间分数阶Fisher方程的数值解法

陈雪娟*,陈景华

(集美大学理学院,福建厦门361021)

摘要：考虑非线性空间分数阶Fisher方程的数值解,提出一种基于二次多项式样条函数的数值解法,并证明该方法具有无条件稳定性和收敛性．为了验证所构造格式的有效性,引入分数阶行方法 (FMOL) 与之进行比较．最后通过一个数值算例说明本文的理论分析是正确的,所构造的离散格式是有效的.

关键词：分数阶扩散方程;Caputo分数阶导数;二次多项式样条函数;行方法

分数阶微分方程(时间、空间或时间空间分数阶)是传统整数阶微分方程的推广．由于分数阶微积分具有记忆和遗传特性,目前已被广泛地应用于模拟工程、物理、化学和其他科学领域的许多现象[1-4]．众所周知,要得到偏微分方程的解析解是很困难的,对于分数阶偏微分方程而言更是如此,常用的方法是借助于各种积分变换和特殊函数的方法[5-7]．近年来许多学者在这个领域里做了大量的研究工作[8-11].

本文考虑非线性空间分数阶Fisher方程的数值解问题,Fisher方程主要用来模拟物种增长和扩散问题．在已有的研究成果中,主要的数值解法是差分法、有限元法和谱方法等,但是采用二次多项式样条函数进行数值逼近的研究文献却较缺乏[12-13]．本文提出一种基于二次样条函数的数值解法,并分析所构造迭代格式的稳定性和收敛性.

1一些记号和简单的结论

非线性空间分数阶Fisher方程如下:

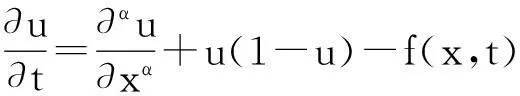
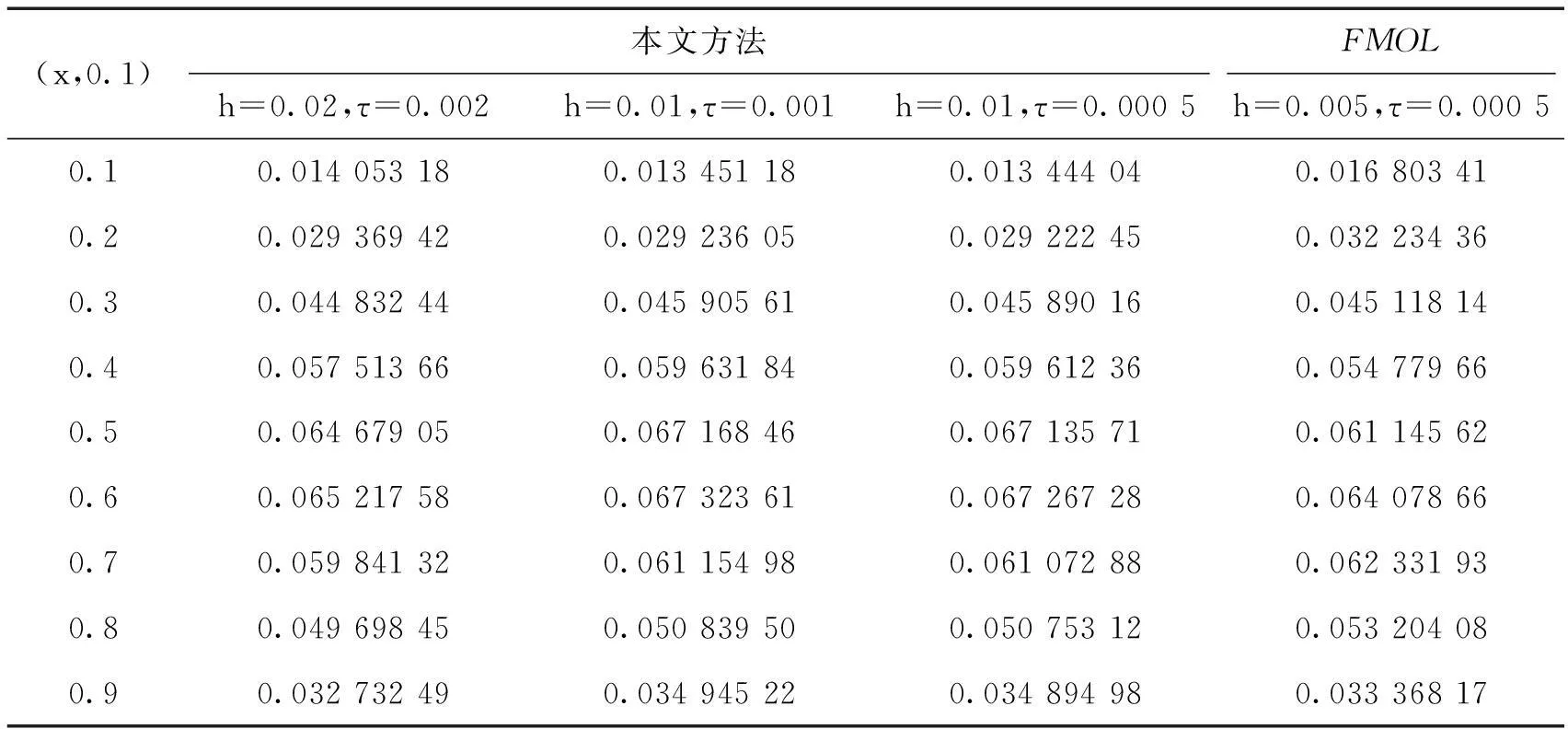
1<α≤2,0

(1)

初始条件和边界条件分别为:

u(x,0)=g(x),0

(2)

u(0,t)=u(l,t)=0,0≤t≤T．

(3)

其中,f(x,t)和g(x)为充分光滑的已知函数,非线性源项是关于u满足Lipschitz 条件.

α阶的Caputo分数阶左导数定义如下：

a

(4)

α阶的Riemann-Liouville分数阶左导数定义如下：

u(s,t)ds,a

(5)

以上2种分数阶导数的定义之间具有如下关系式[14]：

(6)

在实际求解微分方程初值问题的过程中,Caputo导数比Riemann-Liouville导数的应用更为广泛而且更具有物理背景[15]．本文采用Caputo分数阶导数定义,即

本文首先利用二次多项式样条函数提出一种逼近Fisher方程数值解的迭代格式,并证明该格式具有无条件稳定性和收敛性．然后给出非线性空间分数阶Fisher方程的分数阶行方法(FMOL),用于验证所构造格式的有效性．最后通过一个数值算例说明本文理论分析的的正确性和可行性.

2基于多项式样条函数的数值解法

2.1二次多项式样条函数

我们考虑如下二次多项式样条函数Pi(x,tj):

Pi(x,tj)=ai(tj)(x-xi)2+bi(tj)(x-xi)+

ci(tj),x∈[xi,xi+1],i=0,1,2,…,m-1;

j=0,1,…,n.

(7)

为了确定函数Pi(x,tj)的系数表达式,首先定义

(8)

(9)

(10)

由等式(7)～(9),可得

(11)

又由等式(10)和Caputo分数阶导数的定义,有

(12)

因此,Pi(x,tj)系数的表达式为

(13)

2.2数值解法的迭代格式

为了使二次函数Pi(x,t)在x=xi,(i=1,2,…m-2.)处满足连续性条件:

Pi(xi,tj)=Pi-1(xi,tj),

由等式(7)和(13),可以推出

(14)

(15)

证明由于

i=1,2,…,m-2;j=0,1,…,n.

(16)

将等式(16)的右边在点(xi,tj)处进行Taylor展开,得到

O(h

4

)．

(17)

证毕.

所以,迭代格式(14)的截断误差阶为O(hα),我们得到

(18)

利用向后差分法

O(τ)

(19)

和等式

(20)

由方程(1)可得:

(21)

将等式(21)代入等式(18),并忽略截断误差τO(hα+τ),可以推出如下的迭代格式:

(22)

设

则式(22)可以写成

(23)

为了求解这个线性代数方程组,我们还需要两个方程．利用边界条件(3),通过线性插值得到下面两个方程:

(24)

(25)

j=1,2,…,n.

因此,我们得到求解非线性空间分数阶Fisher方程(1)的数值方法.

3收敛性和稳定性分析

首先,将迭代格式(23)写成矩阵的形式

AUj=δBUj-1+δτBFj-1,

(26)

其中,

j=1,2,…,n.

A=

B=

这里,a=δ-τ,b=2τ+6δ．A和B都是对称矩阵．而且A是严格对角占优矩阵,所以矩阵A是非奇异的．设A-1是A的逆矩阵,则由矩阵(26)可得

Uj=δA-1BUj-1+δτA-1BFj-1.

(27)

记

3.1稳定性分析

记

由等式(27),可得误差满足

εj=δA-1Bεj-1+δτA-1Bβj-1,

这里,

k=1,2,…,m-2.

(28)

容易看出,矩阵B的特征值绝对值的最大值为

(29)

矩阵A的特征值绝对值的最小值为

(30)

所以

(31)

由于βj-1满足Lipschitz条件,所以存在L使得

其中L是个正的常数.所以

(32)

将(32)迭代n次,可得

因此,迭代格式(23)是无条件稳定的.

3.2收敛性分析

设

由等式(27),误差满足

ej=δA-1Bej-1+δτA-1Bηj-1+τA-1Rj,

这里,

类似地,可得

所以

利用离散Gronwall不等式,可得

C1TeLT(τ+hα)=C(τ+hα).

其中,C是个正的常数．因此,迭代格式(23)是无条件收敛的.

4FMOL

由于非线性偏微分方程的精确解很难通过计算得到,为了说明所构造的隐式差分格式的计算有效性及理论分析的正确性,我们给出了空间分数阶Fisher方程的FMOL[17-18].

u(xk-1,tj)][(i-k+1)2-α-(i-k)2-α]}+

2u(xi-k+1,tj)+u(xi-k,tj)]}+

tj)-2u(xi-k+1,tj)+u(xi-k,tj)]}+O(h2).

那么Caputo分数阶导数的数值近似可以由下面表达式计算得到:

u(xi-k+1,tj)+u(xi-k,tj)]}，

因此,空间分数阶Fisher方程的行方法可以写成如下形式:

5数值例子

为了证明我们的理论结果,考虑如下非线性空间分数阶Fisher方程:

(33)

表1给出当α=1.5,T=0.1,l=1.0时用隐式格式(23)～(25)和FMOL计算方程(33)的数值结果．可以看出,使用迭代格式(23)～(25)计算所得的数值解与理论分析完全吻合,而且与用FMOL计算所得的数值解非常接近．图1给出了当α=1.5,m=100,n=200时,含非线性源项的扩散系统随时间t变化的特征.

图1　空间分数阶Fisher方程当α=1.5,h=0.01,τ=0.000 5时随时间t变化的性态Fig.1Comparison of the response of the space-Fractional Fisher′s equation at different times when α=1.5,h=0.01,τ=0.000 5

表1　当α=1.5,T=0.1,l=1.0 时,本文所提出的数值方法对应于不同的时间和

6结论

本文给出了非线性空间分数阶Fisher方程的数值模拟,并证明该数值方法是无条件稳定和收敛的．通过一个数值例子的结果证明了本文的理论分析的有效性．该数值方法和理论分析方法也能用来求解和分析其他类型的分数阶偏微分方程.

参考文献：

[1]PODLUBNYI．Fractionaldifferentialequations:anintroductiontofractionalderivatives,fractionaldifferentialequations,tomethodsoftheirsolutionandsomeoftheirapplications[M]．NewYork:AcademicPress,1999:50-84.

[2]HILFERR．Applicationsoffractionalcalculusinphysics[M]．Singapore:WorldScientific,2000:377-385.

[3]METZLERR,KLAFTERJ．Therandomwalksguidetoanomalousdiffusion:afractionaldynamicsapproach[J]．PhysRep,2000,339(1):1-77.

[4]HILFERR．FractionaldiffusionbasedonRiemann-Liouvillefractionalderivatives[J]．JPhysChemB,2000,104:3914-3917.

[5]MAINARDIF,LUCHKOY,PAGNINIG．Thefundamentalsolutionofthespace-timefractionaldiffusionequation[J]．FractCalculusApplAnal,2001,4 (2):153-192.

[6]段俊生,徐明瑜．分数阶扩散方程半无界混合问题的解[J]．高校应用数学学报：A辑,2003,18(3):259-266.

[7]HUANGF,LIUF．Thefundamentalsolutionofthespace-timefractionaladvection-dispersionequation[J]．JApplMathComputing,2005,18:339-350.

[8]LIUF,ANHV,TURNERI．NumericalsolutionofspacefractionalFokker-Planckequation[J]．JCompApplMath,2004,166:209-219.

[9]MEERSCHAERTMM,TADJERANC．Finitedifferenceapproximationsforfractionaladvection-dispersionflowequations[J]．CompApplMath,2004,172:65-77.

[10]ELDANAFST,HADHOUDRA．ParametricsplinefunctionsforthesolutionoftheonetimefractionalBurger′sequation[J]．ApplMathModel,2012,36:4557-4564.

[11]ZAHRAWK,ELKHOLYMS．Quadraticsplinesolutionboundaryvalueproblemoffractionalorder[J]．NumerAlgor,2012,9:373-391.

[12]KHANNA,AYAZM,JINL,etal．Onapproximatesolutionforthetime-fractionalreaction-diffusionequationoffishertype[J]．InternationalJournalofthePhysicalSciences,2011,6(10):2483-2495.

[13]ELDANAFTS,HADHOUDAR．ComputationalmethodforsolvingspacefractionalFisher′snonlinearequation[J]．MathematicalMethodsintheAppliedSciences,2014,37(5):657-662.

[14]ZHUANGP,LIUF,ANHV,etal．Numericalmethodsforthevariable-orderfractionaladvection-diffusionwithanonlinearsourceterm[J]．SIAMJNumerAnal,2009,47:1760-1781.

[15]郭柏灵,蒲学科,黄凤辉．分数阶偏微分方程及其数值解[M]．北京:科学出版社,2011:92-110.

[16]YANGSL．Eigenvalueoftridiagonalmatrixanditsapplications[J]．MathematicsinPracticeandTheory,2010,40(3):155-160.

[17]LIUF,ANHV,TURNERI．NumericalsolutionofthespacefractionalFokker-Planckequation[J]．JournalofComputationalandAppliedMathematics,2004,166:209-219.

[18]LIUF,ANHV,TURNERI,etal．Numericalsimulationforsolutetransportinfractalporousmedia[J]．ANZIAMJ．2004,45(E):461-473.

[19]DIEGOMURIOA．Implicitfiniedifferenceapproximationfortimefractionaldiffusionequations[J]．ComputersandMathwithApplications,2008,56:1138-1145.

Numerical Simulation for the Space Fractional Fisher′s Nonlinear Equation

CHEN Xuejuan*,CHEN Jinghua

(School of Sciences,Jimei University,Xiamen 361021,China)

Abstract:A numerical method based on the quadratic polynomial spline function is used to find approximate solutions for the space fractional Fisher′s nonlinear equation．The proposed method is proved to be unconditionally stable and convergent．For the purpose of evaluating the efficiency of the method,a comparison with a fractional method of lines (FMOL) is made．Finally,a numerical example is presented to show that the theoretical analysis in this paper is both correct and effective.

Key words:fractional diffusion equation;Caputo fractional derivative;quadratic polynomial spline function;line method

doi：10.6043/j.issn.0438-0479.2016.03.010

收稿日期：2015-07-03录用日期：2015-10-25

基金项目：福建省教育厅项目(KB14014)；集美大学留学基金

*通信作者：chenxuejuan@gmail.com

中图分类号:O 241.82

文献标志码：A

文章编号：0438-0479(2016)03-0360-06

引文格式：陈雪娟,陈景华.非线性空间分数阶Fisher方程的数值解法.厦门大学学报(自然科学版)，2016,55(3)：360-365.

Citation：CHEN X J,CHEN J H．Numerical simulation for the space fractional Fisher′s nonlinear equation.Journal of Xiamen University(Natural Science)，2016,55(3)：360-365．(in Chinese)