北斗三类卫星精密星历内插方法分析比较

汪威,陈明剑，闫建巧，尹子明，刘天恒

(信息工程大学 导航与空天目标工程学院,郑州 450001)

北斗三类卫星精密星历内插方法分析比较

汪威,陈明剑，闫建巧，尹子明，刘天恒

(信息工程大学 导航与空天目标工程学院,郑州 450001)

摘要：全球连续监测评估(iGMAS)分析中心能够提供GPS/BDS/GLONASS三系统卫星精密星历、精密钟差、电离层与对流层等产品,在使用北斗卫星进行高精度定位过程中必须对北斗精密星历进行内插。由于我国北斗卫星导航系统(BDS)包含不同轨道的卫星,因此,本文选取iGMAS分析中心精密星历,采用拉格朗日多项式内插和切比雪夫多项式拟合两种方法分别进行北斗GEO/IGSO/MEO三类卫星三维坐标内插实验,分析两种插值方法对不同轨道卫星插值误差与多项式的阶数之间的关系。计算结果表明,两种算法适合北斗不同轨道卫星内插,并且不同轨道卫星达到最佳插值精度所取的阶数不同。

关键词：iGMAS;北斗精密星历;拉格朗日插值;切比雪夫多项式拟合

0引言

在GNSS定位中,高动态运行的GNSS卫星位置为已知值,它是一种原始数据误差,对用户的定位精度有直接影响。在卫星导航定位过程中,广播星历由于其实时性,得到了广泛的应用,但是精度不能满足高精度定位的需要[1]。为了降低星历误差对用户定位精度的影响,IGS组织免费提供不同等级精度与时延的精密星历产品,最终精密星历精度优于5 cm[2]。基于北斗高精度定位的需要,我国成立了iGMAS,能为用户提供高精度的精密星历,精密钟差,电离层与对流层等产品,由于其它一些因素,目前还没有公开发布北斗精密星历。iGMAS分析中心提供的精密星历间隔为15 min的卫星三维坐标,因此,要想得到任意时刻北斗卫星坐标就必须对精密星历进行高精度内插。目前常用的插值方法主要有拉格朗日多项式插值法、内维尔插值法、牛顿插值法、三次样条插值法、三角多项式插值法和切比雪夫多项式插值法等[3,5]。但以上方法均针对GPS卫星精密星历而言,对北斗卫星精密星历很少涉及。由于北斗卫星导航系统(BDS)采用的是混合星座,包含GEO、IGSO、MEO,其中MEO卫星与GPS一样均为中轨轨道卫星,但是地球静止轨道卫星GEO与倾斜地球同步轨道卫星IGSO与GPS还是有一定的区别,如利用广播星历拟合算法在对GEO进行卫星位置计算时需要对拟合参考面进行一个角度旋转。因此,本文以iGMAS分析中心精密星历为例,分析拉格朗日多项式内插与切比雪夫多项式拟合对北斗精密星历的影响,得出一些结论并为以后的深入研究提供参考。

1插值与拟合算法数学模型

1.1拉格朗日多项式内插[6]

假设已给区间[a,b]上的节点x0,x1,…,xn,函数y=f(x)在区间[a,b] 上有n+1阶导数,且y=f(x)在xi的值为yi=f(xi),Pn(x) 是通过yi=f(xi)数据点的不超过n的多项式,则Pn(x)是唯一的,且对区间[a,b]内任意x的n阶拉格朗日的多项式可表示为

(1)

在进行n阶拉格朗日多项式内插任意时刻的卫星位置,需要选取一个区间[ta,tb],使得t∈[ta,tb],并且在所选区间内满足m≥n+1,其中,n为插值阶数,m为插值节点个数,拉格朗日多项式函数模型简单,易于编程实现,是经典的插值算法,但是插值节点的增删则需要重新构造多项式,利用式(1)计算卫星的三维坐标可以表示为

(2)

1.2切比雪夫多项式拟合[9]

切比雪夫多项式拟合的原理是通过根据给定的一些数据拟合出一个逼近函数,使其在给定的函数值与给定值之间的方差和达到最小,且该函数是以切比雪夫多项式为函数的,在多项式阶数发生改变时只需改变多余观测量,无需额外增加新的节点,原有的公式不需要再重新建立。由于切比雪夫多项式只适用于自变量区间为[-1,1]的情况,因此在采样时间段[t0,t0+Δt]内(t0为初始时刻,Δt为拟合时间长度)采用n阶切比雪夫多项式拟合时,首先需要利用下述公式将时间进行标准化

(3)

将时间变量t的区间归化到变量区间[-1,1]后,则GNSS卫星的切比雪夫的多项式拟合表达式在卫星的三个分量可以表示为

(4)

式中: n为切比雪夫多项式的阶数; Cxi,Cyi,Czi分别为 卫星在X,Y,Z三个坐标分量方向的切比雪夫多项式系数。则第i阶切比雪夫项式Ti则表示为

(5)

通过式(4)可计算出t∈[t0,t0+Δt]时间区间内任意时刻的卫星坐标。

1.3实验设计过程

iGMAS分析中心精密星历通用格式为AACwwwwd.sp3的文本文件,其中AAC为各分析中心三字符英文首字母缩写,wwww为北斗周计数(四位数字),不足四位最前补零,d取0到6为天文件,取0为周日,其具体格式说明如图1所示。

图1　北斗精密星历数据格式

从图1可以看出,北斗精密星历文件由头文件与数据记录文件组成,基本格式与IGS分析中心发布的精密星历格式差别不大。图1飘红的部分中第一行“LSN”代表北斗精密星历发布机构之一,第二行“484”表示北斗周,第三至六行表示多系统卫星数目及列表,第二十三行“M”与“BDT”分别表示混合系统与北斗时,第三十二行/*表示头文件结束标志。数据记录历元以*开始,按照卫星列表顺序依次给出卫星的三维坐标与钟差。

由于卫星的精密星历是根据大量的观测数据并通过严密的平差计算得来,其轨道变化是平滑的,由上面介绍,卫星坐标是以15 min间隔X,Y,Z的形式给出,实验设计基本思路为读取*.sp3数据,构造坐标与时间之间的函数关系,通过编程实现对任意时刻卫星位置的计算,其程序设计流程图如图2所示。

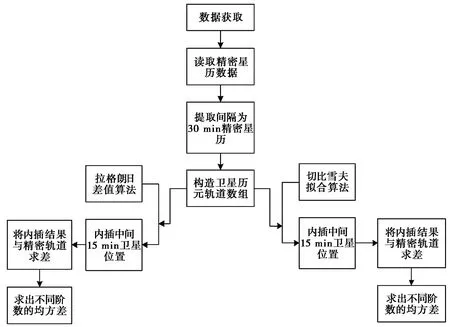
图2　卫星星历插值设计流程图

2算例分析与比较

为了分析北斗不同轨道卫星的插值精度与插值阶数的关系,本文选取了iGMAS分析中心精密星历数据,起始历元为2015年4月16日0时0分0秒,终止历元时刻为2015年4月16日23时45分0秒的.sp3精密星历数据作为对象进行内插计算,方法采用拉格朗日与切比雪夫多项式拟合两种插值算法。选择的卫星包含北斗混合星座的三类卫星,选取的卫星号为PC02(GEO)、PC08(IGSO)和PC14(MEO),在实验过程中将拟合的时间间隔设为30 min,将30 min间隔的历元作为内插点计算各个内插时间段中间时刻的卫星位置,将内插值与真值进行比较,计算出残差的均方差。根据以上分析,利用Visual Fortran编程语言进行了实现,表1、表2与表3分别给出了PC02、PC08和PC14号三颗卫星7～20阶的拉格朗日与切比雪夫内插均方差结果,图3、图4与图5为根据表1、表2与表3绘制出插值精度图随阶数的变化关系。为了更能直观地反映插值结果情况,文中绘制了插值结果残差图,鉴于文章篇幅,文章以PC08卫星为例画出两种插值算法最佳插值结果残差分布图,结果如图6和图7所示。

2.1GEO卫星精密星历插值精度分析

从表1与图3可以看出,PC02(GEO)卫星的插值精度随着阶数的增加而发生变化。对于拉格朗日插值算法,GEO卫星三维坐标分量表现在8～12范围内精度变化比较平稳。超过14阶精度有所下降,当阶数超过17阶时精度明显变差,拉格朗日在取10阶时精度达到最高。GEO卫星三维坐标插值精度表现在z坐标插值精度大于x与y,小于16阶时,x与y精度几乎相等,当超过16阶以上表现在插值精度z>x>y;对于切比雪夫多项式拟合,GEO卫星三维坐标分量表现在阶数小于8阶时,精度比较差。在8～12范围内精度变化比较平稳,当阶数超过17阶时精度明显变差,切比雪夫在取9阶时精度达到最高。采用切比雪夫多项式拟合GEO卫星三维坐标精度表现在阶数小于8阶时z>x>y,在8～14阶范围内表现在x插值精度最高,y与z精度相当,在14～16范围内表现在x>y>z.

2.2IGSO卫星精密星历插值精度分析

从表2与图4可以看出,PC08(IGSO)卫星的

插值精度表现在当插值阶数过高或者过低时,插值精度效果都非常差。对拉格朗日插值算法,在8～11阶范围内,随着阶数的增加插值精度有所提高。当阶数取9时,可以达到厘米级的精度。在11～14阶达到毫米级,并且在取12阶时精度最高,超过18阶插值精度明显为下降。在8～10阶范围内IGSO三维坐标分量表现在z>x>y,在10～12阶时表现在y与z精度相当均高于x,12～18阶表现在y>x>z;对于切比雪夫多项式拟合,IGSO卫星三维坐标分量表现在阶数小于9阶时精度比较差。在12～16阶范围内精度变化比较平稳,当阶数超过17阶时精度明显变差。当阶数取11时,可以达到厘米级的精度。在12～14阶可以达到毫米级,在取13阶时精度最高。在阶数小于11阶时z>x>y,在11～13阶范围内表现在z>y>x.在13～17阶范围内表现在y>x>z．

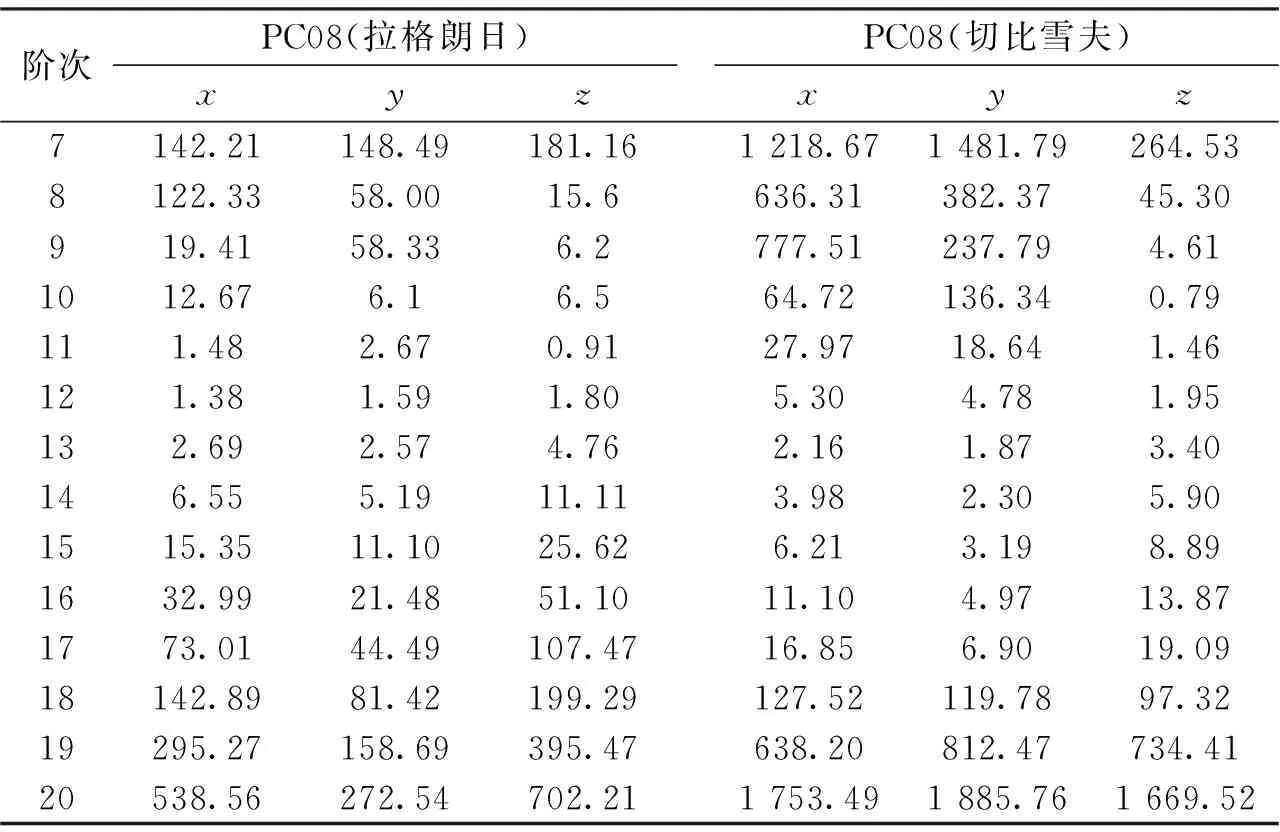
表2　IGSO卫星两种插值方法结果对比

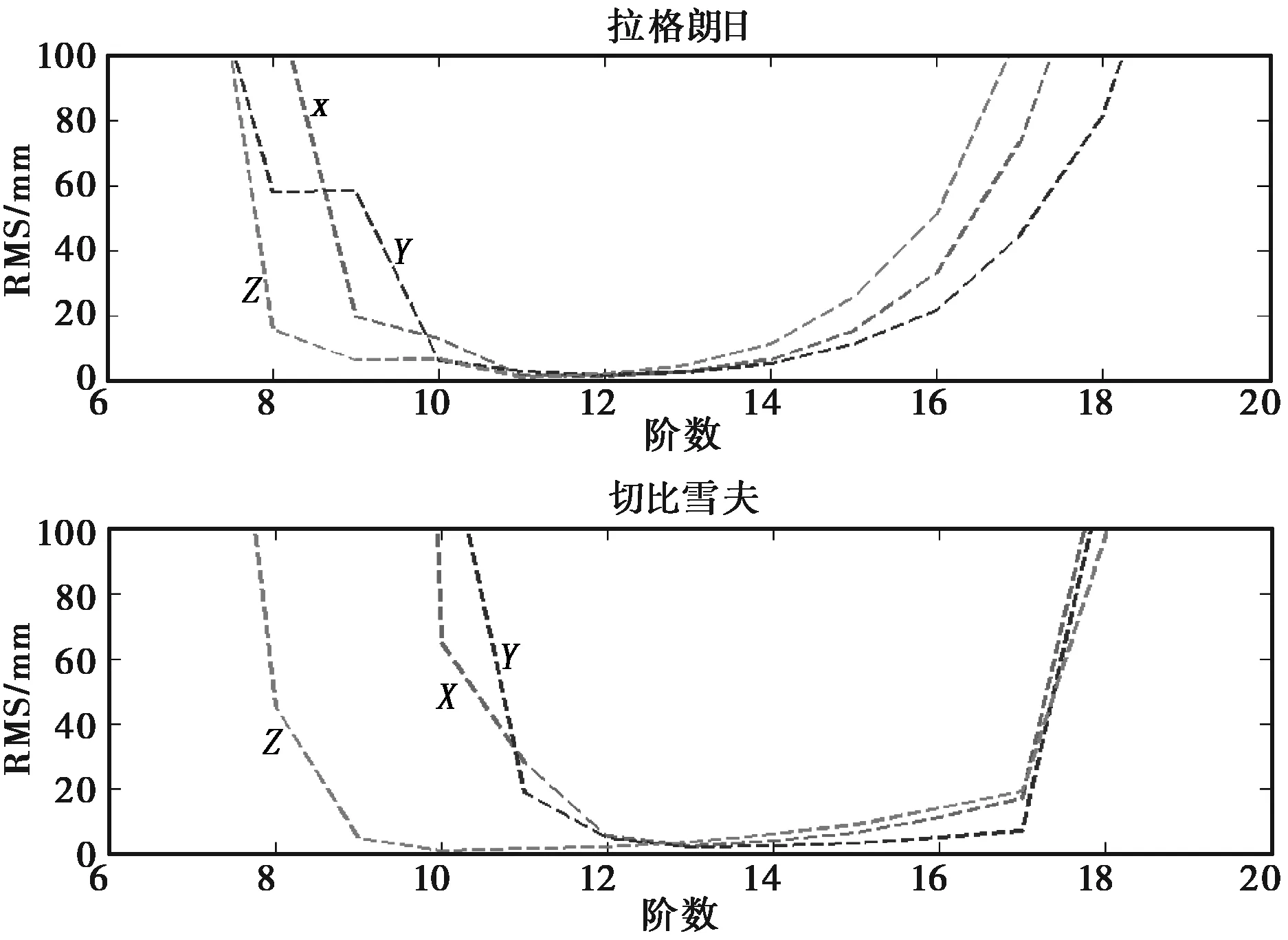
图4　两种插值算法对IGSO卫星插值误差　　　随阶数变化关系

2.3MEO卫星精密星历插值精度分析

从表3可以看出,对PC14(MEO)卫星的插值精度表现在当插值阶数过高或者过低时,插值精度效果都非常差。对拉格朗日插值算法,在9～12阶范围内,随着阶数的增加插值精度有所提高。当阶数取11阶时可以达到厘米级的精度,在13与14阶时达到毫米级,超过18阶插值精度明显为下降,并且在取12阶时精度最高。在9～11与13～16阶时MEO三维坐标分量表现在z>x>y,在16～18阶表现在月x>z>y;对于切比雪夫多项式拟合,MEO卫星三维坐标分量表现在阶数小于10阶时精度比较差,在14～17阶范围内精度变化比较平稳,当阶数超过17阶时精度明显变差,当阶数取12时,可以达到厘米级的精度,14～16阶可以达到毫米级,在取14阶时精度最高,超过18阶插值精度明显为下降。在小于12阶时三维坐标分量表现在z>x>y,在14～17阶范围内表现在z>x>y;图5示出的是两种插值算法不同阶次对PC08(IGSO)卫星的插值残差图。

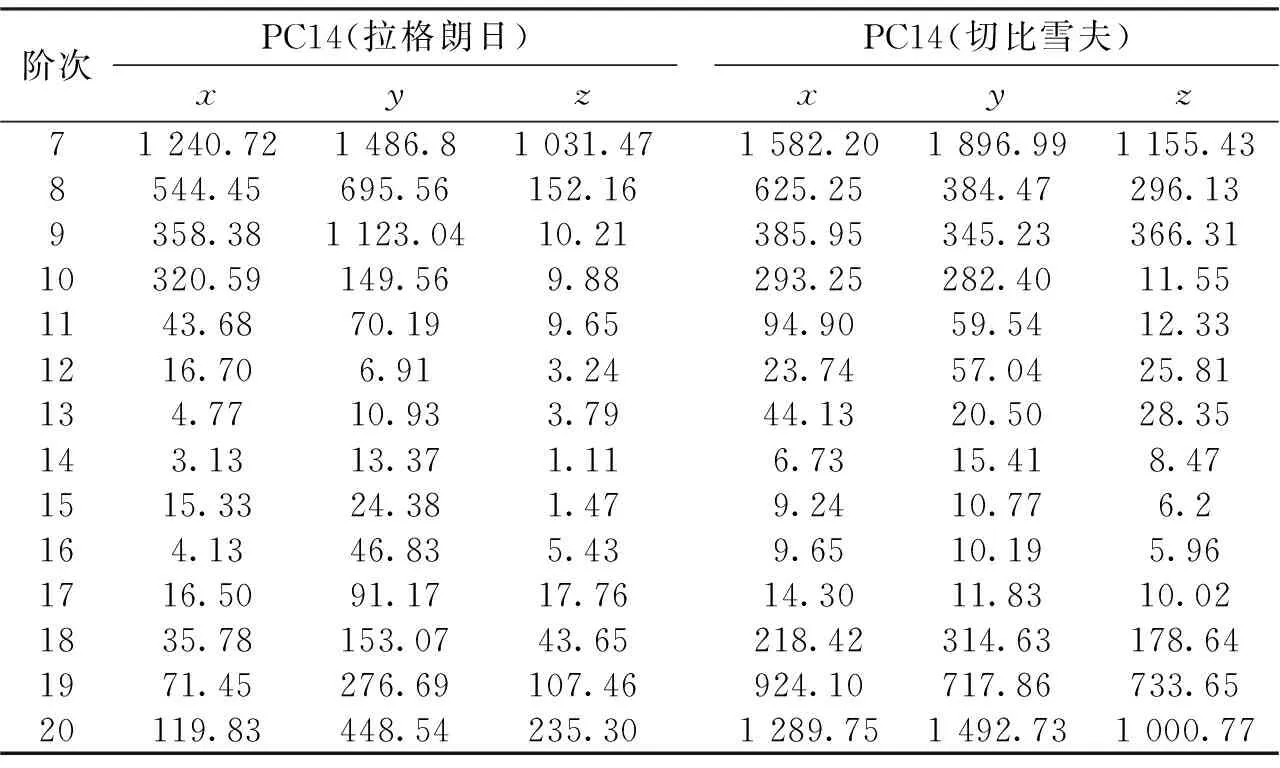
表3　MEO卫星两种插值方法结果对比

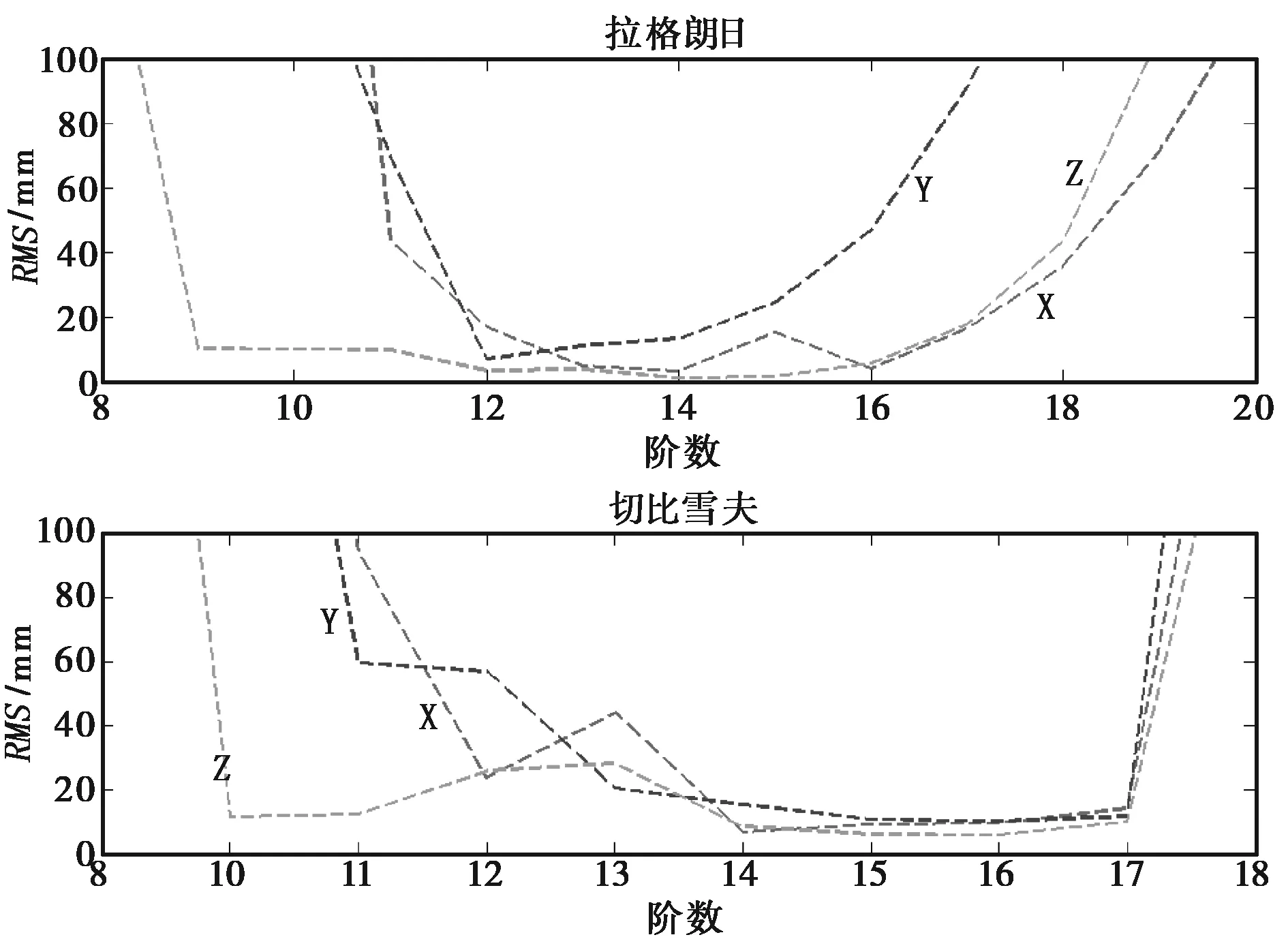
图5　两种插值算法对MEO卫星插值误差　　　随阶数变化关系

从图6与图7可以看出,无论采用何种插值算法,当取算法达到最佳阶数时,卫星的插值精度能够保持在毫米的范围之内。

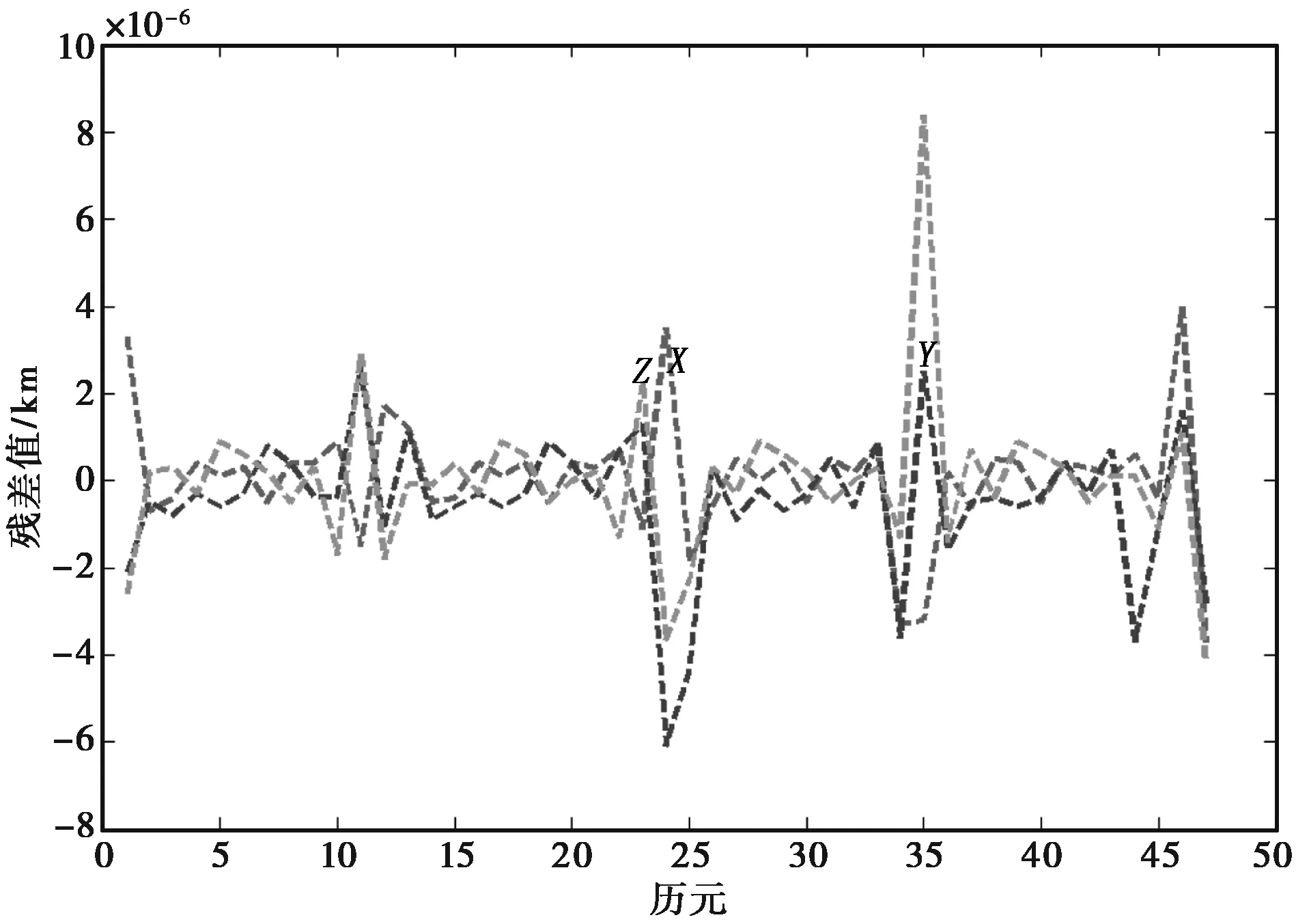
图6　拉格朗日12阶插值残差图

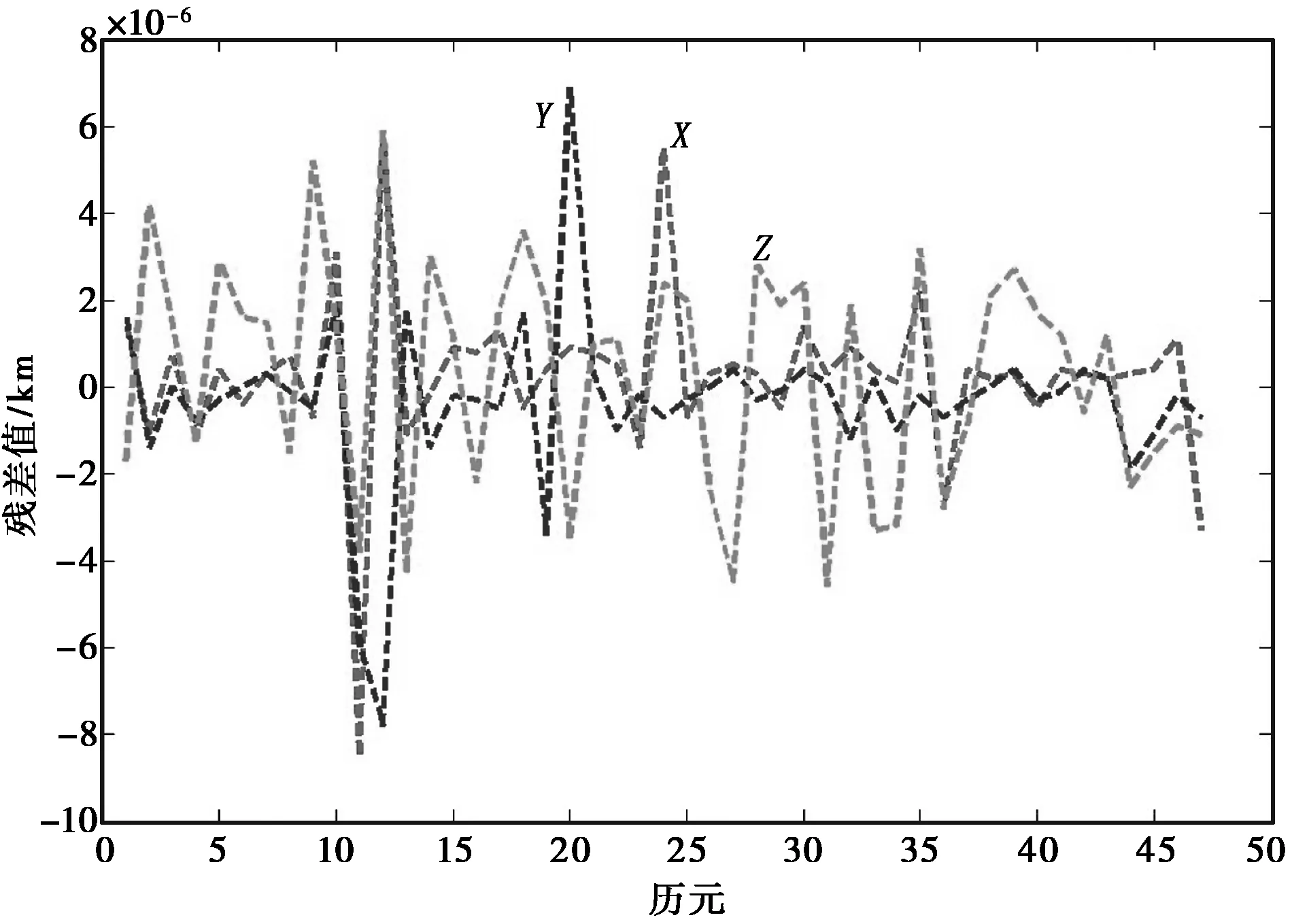
图7　切比雪夫13阶插值残差图

3结束语

1) 本文以北斗系统三颗不同轨道卫星分析了拉格朗日插值与切比雪夫拟合对卫星精密星历插值实验,结果分析表明,拉格朗日插值与切比雪夫多项式拟合适合于北斗不同轨道卫星的精密星历内插。

2) 在阶数选取方面两种方法插值阶数都不应过低或者过高,GEO卫星对两种插值算法在9～13阶范围内插值结果比较好。IGSO卫星对于拉格朗日在11～14阶范围内插值结果比较好,对切比雪夫在12～15阶插值结果较好。MEO卫星对于拉格朗日在12～14阶插值结果比较好,对切比雪夫在14～16阶范围内插值结果比较好,超出17阶三类卫星的插值精度较差。同种插值算法对不同轨道卫星达到最佳精度所取的阶数不同,不同插值算法对同一类卫星的最佳插值阶数也不相同。

3) 卫星轨道的三个坐标分量的插值精度在取同一插值阶数时插值精度不同,并且卫星的三个坐标分量达到最佳插值精度所取的阶数也不完全相同。因此,在进行卫星精密星历内插计算时可以对三个坐标选取不同的插值阶数,以期达到精度最优。

参考文献

[1]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.

[2]马俊,唐诗华,黄鹰,王文杰,等.基于IGS精密星历的卫星位置内插方法比较[J].城市勘测,2011(5):89-93.

[3]洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报·信息科学版,2006,31(6):516-518.

[4]KOUBBA J,PIERRE. Precise Point Positioning using IGS orbit and clock products[J].GPS Solutions,2001,5(2):12-28.

[5]任锴,杨力,郭玉良,等.卫星星历计算研究[J].海洋测绘,2008(1):31-34.

[6]彭泽泉.GPS精密星历拟合方法的研究[J].测绘科学,2010,35(增1):63-65.

[7]孙腾科基于拉格朗日与切比雪夫方法的精密星历插值研究[J].测绘与空间地理信息,2014,37(2):33-37.

[8]陈兆林,张书毕,佟瑞菊用拉格朗日多项式内插计算GPS卫星位置[J].全球定位系统,2007,33(2):33-35.

[9]刘玉虎.航天器轨道确定——卫星坐标的插值与拟合方法[D].西安:西安电子科技大学,2014.

汪威(1989-),男,硕士生,主要研究方向为北斗CORS关键技术。

陈明剑(1976-),男,副教授,研究方向为GNSS精密单点定位及地基增强系统建设及其应用。

闫建巧(1989-),女,硕士生,研究方向为精密单点定位相关技术研究。

尹子明(1990-),男,硕士生,研究方向为基于CORS的BDS数据质量分析。

刘天恒(1990-),男,硕士生,主要研究方向为网络RTD技术应用研究。

Three Kinds of Compass Satellite Precise Ephemeris Interpolation Method Analysis Comparative

WANG Wei，CHEN Mingjian,YAN Jianqiao, YIN Ziming,LIU Tianheng

(1.SchoolofNavigationandAerospaceEngineering,InformationEngineeringUniversity,Zhengzhou450001,China)

Abstract: The global continuous monitoring and assessment iGMAS analysis center can provide GPS/BDS/GLONASS three system satellite precise ephemeris and precision clock error, ionosphere and troposphere products and so on.High precision positioning process must be carried out on the precise ephemeris interpolation using compass satellite, Because of our country's Beidou satellite navigation system (BDS) contains different orbits of the satellite, therefore,This paper selects the iGMAS Analysis Center precise ephemeris, Using Lagrange polynomial interpolation and Chebyshev polynomial fitting two methods respectively Beidou GEO/IGSO/MEO three kinds of satellite Three dimensional coordinate interpolation experiments, Two interpolation methods are analyzed to analyze the relationship between the interpolation errors of different orbit satellites and the order of polynomial. and draws some conclusions. The calculation results show that the two algorithms are suitable for the interpolation of different orbit satellites, and the order of the different orbit satellites to achieve the best interpolation accuracy is different.

Keywords:International GNSS monitoring and assessment system; compass precise ephemeris; Lagrange interpolation; Chebyshev polynomial fitting

doi:10.13442/j.gnss.1008-9268.2016.02.011

收稿日期：2016-01-12

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2016)02-0060-06

作者简介

资助项目： 装备科研基金项目(编号：9140A24011314JB52001)

联系人： 汪威E-mail:1101019365@qq.com