基于ITRF2008的NNR-MORVEL56的全球板块运动参数求解

李亚萍,孙付平,门葆红,刘婧,蔡韧鸣,肖乐杰

(1.信息工程大学 导航与空天目标工程学院,郑州 450000;2.信息工程大学地理空间信息学院,郑州 450000)

基于ITRF2008的NNR-MORVEL56的全球板块运动参数求解

李亚萍1,孙付平1,门葆红2,刘婧1,蔡韧鸣1,肖乐杰1

(1.信息工程大学 导航与空天目标工程学院,郑州 450000;2.信息工程大学地理空间信息学院,郑州 450000)

摘要：基于最新的、较为完善的板块边界模型——NNR-MORVEL56的划分边界,利用ITRF2008的数据解建立实测板块运动模型ITRF2008VEL,对NNR-MORVEL56的部分板块欧拉参数进行求解,并给出误差估计;在此基础上,以NNR-MORVEL56模型的欧拉参数为初始值,利用其理论速度与实测速度差值,求参数改正数,进而迭代求出参数最优解,并与ITRF2008VEL、NNR-MORVEL56进行比较;结果表明,迭代最优解在精度上优于ITRF2008VEL,且三种模型在整体上有一定的一致性,但也存在部分差异;此外,虽然利用ITRF2008的数据可以解算部分NNR-MORVEL56的板块欧拉参数,但仍有局限性。

关键词：NNR-MORVEL56;ITRF2008VEL;欧拉参数;误差估计;迭代最优解

0引言

空间观测技术以精确、实时、直接、系统、全面地监测地球微小动态变化的优点成为当今研究地壳运动和地球动力学最精密、最直观的观测手段,从根本上突破了经典大地测量的时空局限性,使地球变化以及地壳运动的监测、研究和应用发生了根本性的变化。特别是近几十年来,空间技术的迅猛发展,利用空间技术检测已有的地学模型已完全成为可能。ITRF系列是在空间大地测量实测数据的基础上建立起来的,采用VLBI、SLR、GPS等技术,综合了多个数据分析中心的解算结果构建了地球参考框架[1],目前,ITRF2008参考框架相比其它序列,测站的位置和站速度的精度方面都有所提高,而且其原点和尺度也都有所改善,是国际地球参考框架的精化版本[2-3]。因此,不少研究利用其站坐标和速度场建立了各个系列的全球板块运动速度场模型,例如ITRF2000VEL[4]、ITRF2005VEL[5]、ITRF2008VEL[6]等。但是这些成果依旧基于NUVEL1A中的14个大板块,并没有将全球

范围“造山带”部分的中小板块划分出来,即没有将板块进行合理的细化。而NUVEL1A被提出于二十世纪九十年代,在这几十年,全球的构造在发生着微小的变化,这些变化是可以探测出来的,所以随着技术的发展,迫切需要更加合理的板块边界模型。NNR-MORVEL56是目前最新的、较为完善的板块边界模型,本文基于NNR-MORVEL56模型的板块划分边界,利用ITRF2008的数据对NNR-MORVEL56的板块参数及其误差进行求解,以NNR-MORVEL56模型参数为初始值通过求解参数差值对参数进行改正,取得欧拉参数的迭代最优解,以此为基础进行模型分析与比较,探求能否利用ITRF2008的坐标速解对NNR-MORVEL56模型划分的合理性进行验证。

1NNR-MORVEL56模型简介

NNR-MORVEL56[7]是Argus在MORVEL和PB2002[8]的基础上提出的,相对于岩石圈无整体旋转的板块模型,描述了无旋转参考架的绝对运动参数,将31个小板块统一到MORVEL中,对全球板块边界进行了重新划分,是对二者的改进,其数据主要为10个不同国家近10年的海洋地球物理、地震、测地数据,比NUVEL-1A用了更多的数据,是目前最为全面的板块边界模型。其中,25个较大板块来自MORVEL,另外31个小板块来自PB2002,并继续引用了PB2002模型中31个板块边界,此外,将Sur、Lwandle板块分别从南美、索马里板块分离出来,Capricorn和Macquarie从澳大利亚板块分离出来。

根据NNR-MORVEL56的板块边界划分情况，以及ITRF2008的台站分布，如图1和图2所示,估计了全球18个板块运动的参数及其误差,18个板块为 Amurian、Antarctic、Arabia、Australia、Cocos、Eurasia、India 、N.America 、Nazca、Nubia、Pacific、Yangtze、Somalia 、Philippine、OK、Sunda 、S.America、Capricorn.图1中字母是各个板块名称的缩写,其全名以及参数等详见文献[9]。

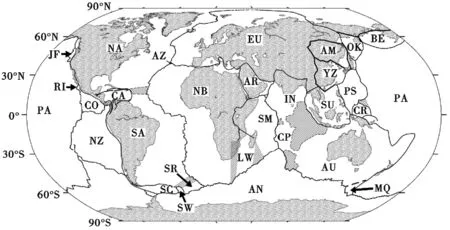
图1　NNR-MORVEL56板块划分图

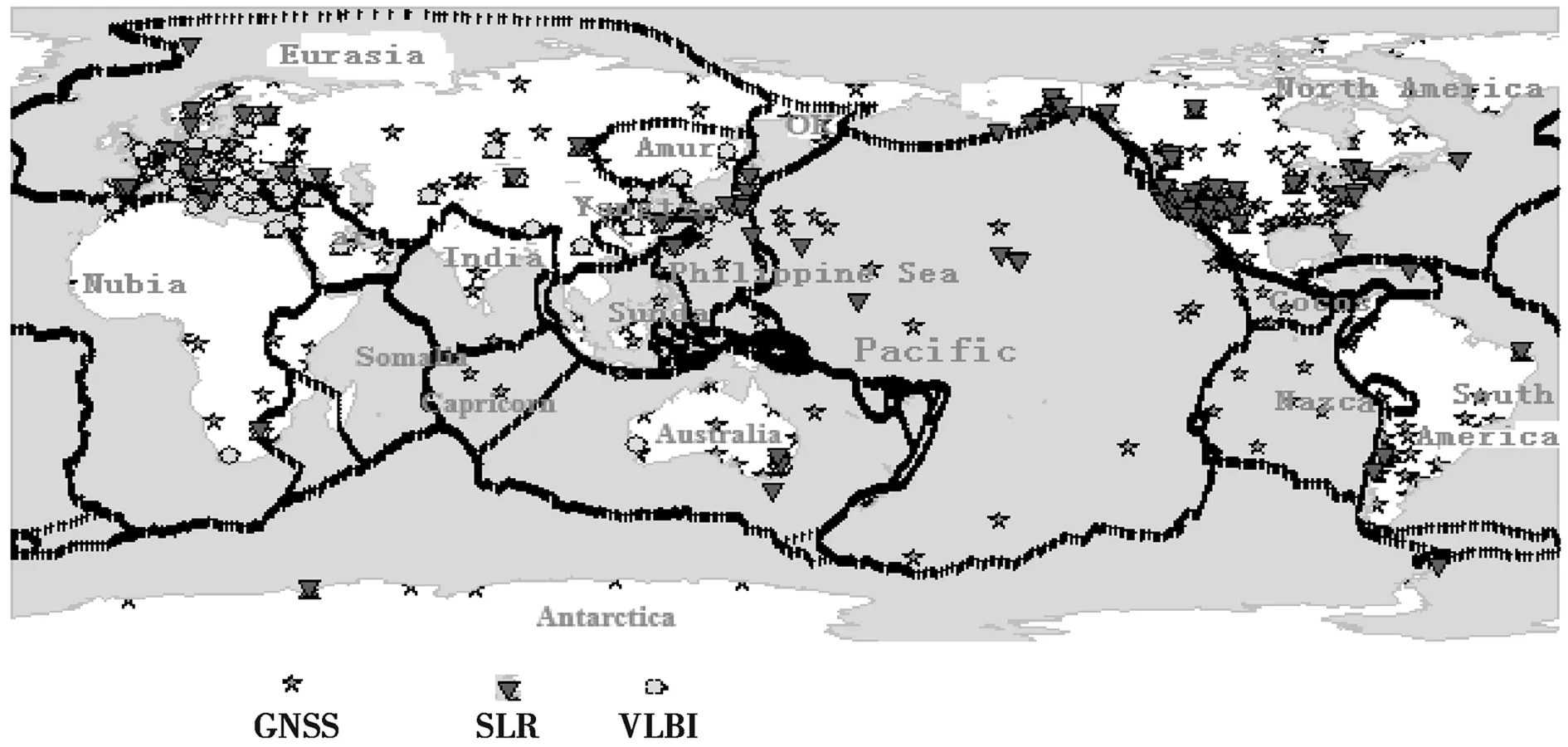
图2　台站在板块内的分布

2计算模型

在板块运动机理研究中,通常假定板块是刚体,而事实上板块并非严格意义上的刚体,板块内局部地区和边界地区都存在着形变。因此,在建立板块运动模型时,必须选择板块稳定主体内的台站,才能完全反映板块的主体运动,可以基本上消除局部形变的影响。为了解算出较高精度的参数,先对下载的数据进行预处理,其目的主要是对测量获取的数据进行一个科学的筛选,从而有效剔除异常数据,尽可能选择块体稳定区域内的台站数据,以保证最后获取的模型参数的正确性。一般选择台站的通用标准[10]:1) 测站连续观测3年以上;2) 位于刚性板块并远离形变区域;3) 同一板块上各测站速度的一致性强,即剔除测站的整体性运动之后,稳定测站的残差站速度应很小。为了尽可能多地保留台站的信息,按照台站选取的原则,对于重复观测的台站,若站速度稍有不同,即当作两个台站来处理。

板块的运动常采用旋转角速度矢量(或欧拉矢量)Ε来描述。根据板块运动理论,每个板块服从欧拉定律,板块运动欧拉矢量Ω与测站地心速度V之间有如下关系为

V=Ω×r，

(1)

式中; r为测站地心位置矢量。如果已知V和r就可估计出Ω.

将式(1)展开:

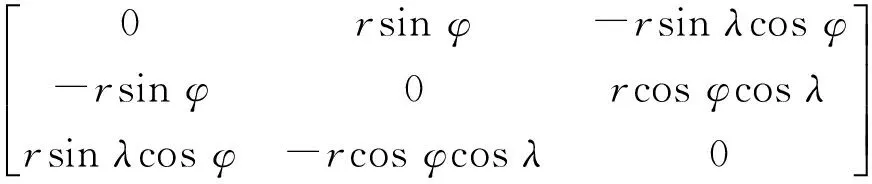
(2)

式中:Vx、Vy、Vz为地心坐标速度；λ、φ为该站地心经纬度;Ωx、Ωy、Ωz为块体运动欧拉向量三分量,因板块运动主要反映在水平站速度之中,况且VLBI、SLR、GPS三种技术确定垂向站速度还不够精确,直接采用地心站速度V可能会使板块运动参数估计受到垂向站速度误差的影响,实用中常把测站地心速度转换为站心速度,并采用其水平分量求解板块运动欧拉矢量Ω[11]。

地心坐标速度转换为站心坐标速度

(3)

式中,Vn、Ve为某站的北、东向站速度。

站心坐标速度与欧拉参数关系式为

(4)

相应的欧拉极为

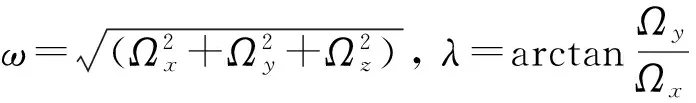
(5)

式中;ω为旋转速率;λ和φ分别为旋转极的经度和纬度。

按式(6)～(8)可计算误差。

水平速度单位权中误差为

钢琴Ⅱ模仿乐队伴奏的效果。演奏者在练习时，内心要清晰地感受到两个八分音符的节奏律动，犹如一个指挥家般掌握稳定的速度，抑制旋律声部“拖延”或“赶”节奏。八分休止符准确，后半拍的跳音要整齐、轻巧，富有动力。演奏时跳音应贴键“拔”起，手腕不能松懈。

(6)

式中,n为已知水平速度个数。

水平速度协方差矩阵为

(7)

欧拉分量差三分量的协方差矩阵为

QΩΩ=KQVVKT.

(8)

(9)

以NNR-MORVEL56欧拉参数作为初始值(Ωx0,Ωy0,Ωz0),按照式(4)求解理论上的测站速度 V,然后求速度差值ΔV,进而求出欧拉参数的改正数。

ΔΩ=(ATPA)-1ATPΔV,

(10)

式中,P设为单位权矩阵。将ΔΩ加到初始值中进行改正,然后求解新的理论站速度,直至迭代到ΔVTΔV=min,这时得到的欧拉矢量即可认为是迭代最优解。

3结果及分析

采用的数据为ITRF2008的速度场,可以从ITRF2008官网上下载得到,采用第2部分内容中的模型公式对板块运动欧拉参数进行了求解,计算结果以及各模型的比较如表1所示,Ⅰ：ITRF2008VEL、Ⅱ：迭代最优解 Ⅲ：NNR-MORVEL56[7]。

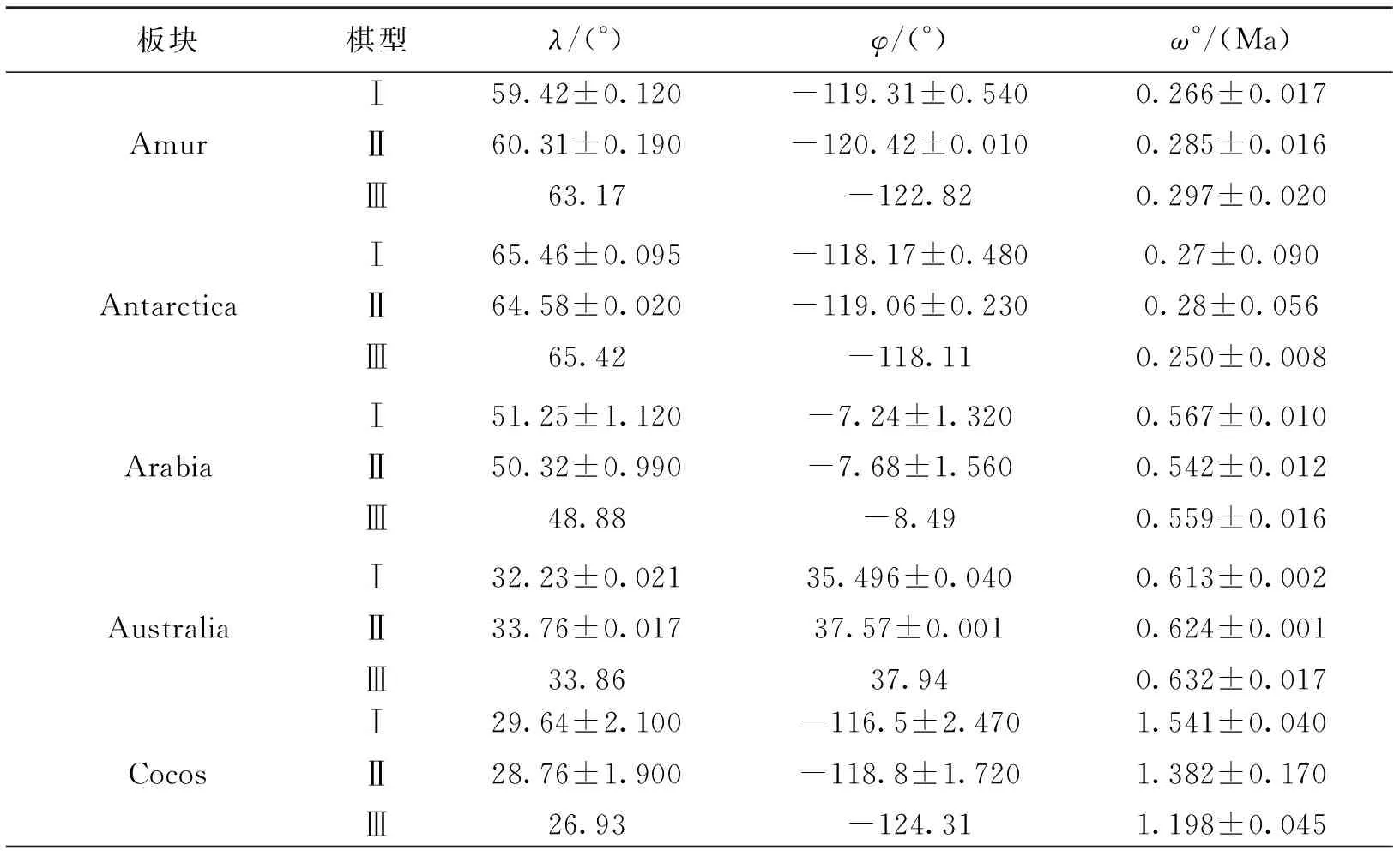
表1　计算结果及比较

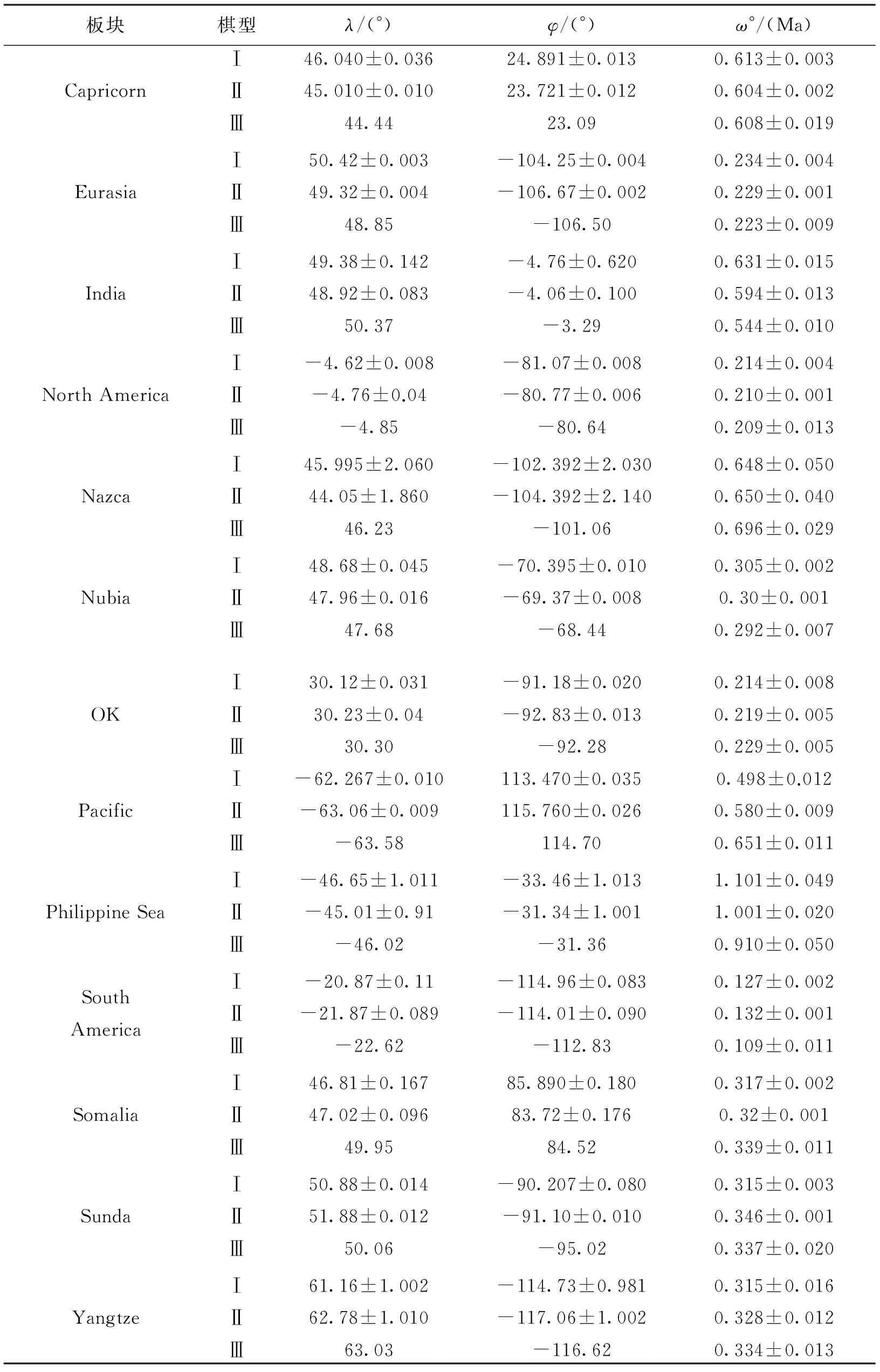
(续表)

4结束语

本文基于NNR-MORVEL56模型的板块划分边界,对ITRF2008的坐标速度解进行了预处理,根据台站在板块分布的情况,选择了可利用的台站数据,估计了NNR-MORVEL56模型的18个板块运动模型参数及其误差。并将ITRF2008VEL、NNR-MORVEL56模型以及基于二者的迭代最优解进行了对比分析,结果表明,模型在整体上保持一致,但也存在部分差异,存在差异的原因是多方面的,例如台站的分布直接影响参数的计算,还有采用的数据的性质:ITRF2008数据解是多种空间技术的组合解,NNR-MORVEL56 模型采用了地学资料中的数据以及部分GPS数据。此外,利用ITRF2008数据解算NNR-MORVEL56模型中的板块运动参数存在缺点,即NNR-MORVEL56 模型中板块划分较之前的模型更细,存在很多微板块,使得原本在同一个大块体上的台站划分两个甚至多个块内,以至于台站分布不均,或者个别板块内没有台站,使得板块的参数求解精度较差甚至无法解算,例如,Lwandle板块虽然从Somalia板块内分离出来,但是仅限于ITRF2008的数据是无法解算其板块运动参数的。由此可知,以NNR-MORVEL56 模型为基础进行板块的运动参数求解,需要搜集更加完善的、覆盖全球范围的高精度数据。

参考文献

[1] 朱新慧.空间地球动力学若干问题研究[D].郑州:信息工程大学，2005.

[2] ALTAMIMI Z, COLLILIEUX X, METIVIER L.ITRF2008: an improved solution of the international terrestrial reference frame[J].Geodesy and Geodynamics, 2011, 85(2):457-473.

[3] 成英燕.框架简介[J].大地测量与地球动力学, 2012, 32(1):47-50.

[4] 金双根, 朱文耀.3种板块绝对运动模型的建立及其比较[J].中国科学院上海天文台年刊, 2002, 23(2):21-27.

[5] 朱新慧,孙付平,王刃现今板块运动模型的发展及其比较[J].测绘科学技术学报, 2010, 27(3):184-188.

[6] ZHU Z, MENG G J. Global crustal movement and tectonic plate boundary deformation constrained by the ITRF2008[J].Geodesy and Geodynamics, 2012, 3(3):40-45.

[7] ARGUS D F, GORDON R G, DEMETS C.Geologically current motion of 56 plates relative to the no-net-rotation reference frame[J].Geochemistry, Geophysics, Geosystems, 2011, 12(11):1-13.

[8] BIRD P. An updated digital model of plate boundaries[J].Geochemistry, Geophysics, Geosystems, 2003,4(3), 10-27.

[9] DEMETS C, GORDON R G, ARGUS D F. Geologically current plate motions[J].Geophysical January International, 2010, 18(1):1-80.

[10]朱新慧.现代地壳运动参考基准的研究[D].郑州:信息工程大学,2009.

[11]孙付平.基于空间技术的现代地壳运动研究[D].上海:中国科学院上海天文台,1994.

李亚萍(1989-),女,硕士生,主要研究方向为大地测量与地壳形变。

孙付平(1964-),男，博士生导师,主要从事地球动力学以及组合导航研究。

门葆红(1966-),女，副教授,主要从事地理信息系统研究工作。

刘婧(1986-),女，讲师,主要从事卫星导航研究。

蔡韧鸣(1993-),男,硕士生,主要研究方向为组合导航算法研究。

肖乐杰(1991-),男,硕士生,主要研究方向为卫星导航算法研究。

Calculation of NNR-MORVEL56 Plate Motion Parameters Based on ITRF2008

LI Yaping,SUN Fuping,MEN Baohong,LIU Jing,CAI Renming,XIAO Lejie

(1.InstituteofNavigationandSpaceTargetEngineering,InformationEngineeringUniversity,Zhengzhou450000,China;2.GeographySpaceInformationInstitute,InformationEngineeringUniversity,Zhengzhou450000,China)

Abstract: Based on the latest and more perfect plate boundary model-NNR-MORVEL56, this paper establishes the plate motion model ITRF2008VEL using ITRF2008 data and obtains the Euler parameter with its error estimation of partial NNR-MORVEL56 plates. Then on this basis, NNR-MORVEL56 Euler parameters is taken as the initial values, and the parameter correction is acquired using the difference between the theoretical velocity and its measurement value. The optimal iterative solutions are calculated and compared with those of ITRF2008VELand NNR-MORVEL56. It is showed that the optimal iterative solutions are better than ITRF2008VEL on the accuracy, and on the whole, three models have certain consistency, but some differences still exist. Moreover, though the ITRF2008 data can be used to calculate the Euler parameter of partial NNR-MORVEL56 plates, some limit is revealed.

Keywords:NNR-MORVEL56; ITRF2008VEL; Euler parameters; error estimation; iterative optimal solution

doi:10.13442/j.gnss.1008-9268.2016.02.003

收稿日期：2015-09-12

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2016)02-0014-06

作者简介

资助项目： 国家自然科学基金(批准号：41374027)

联系人： 李亚萍 E-mail: 572118590@qq.com