基于多项式模型的改进卫星钟差预报方法

马卓希,杨力,贾小林,赵海山

(1.信息工程大学 导航与空天目标工程学院,郑州 450001;2 西安测绘研究所,西安 710054)

基于多项式模型的改进卫星钟差预报方法

马卓希1,杨力1,贾小林2,赵海山1

(1.信息工程大学 导航与空天目标工程学院,郑州 450001;2 西安测绘研究所,西安 710054)

摘要：根据卫星钟固有的特性,提出了一种通用的卫星钟差预报方法。该方法在多项式模型的基础上,对多项式模型的选择、周期项修正、残差建模等方面进行了改进。首先利用拟合数据的残差标准差指标进行多项式模型的自适应选择,继而利用频谱分析的方法对钟差序列的周期项进行了建模,最后利用AR模型对消除趋势项的随机项进行建模。试验结果表明，改进的钟差预报模型能够显著地提高钟差的预报精度,对于稳定度较差的卫星的预报效果尤为显著。改进模型的卫星钟预报6 h预报精度总体优于1 ns,24 h预报精度优于2 ns.

关键词：GPS;星载原子钟;多项式模型;钟差预报

0引言

卫星轨道及精密钟差的预报一直是实时高精度定位领域的重要研究内容。IGS组织向用户发布事后、快速及超快速的卫星轨道和钟差产品。GPS的超快速的预报轨道和钟差产品的精度分别为5 cm和3 ns左右[1]。近年来,精密轨道的预报精度得到了较大幅度的改进,然而卫星钟差的预报精度相对较差,难以满足亚分米级的实时精密单点定位的需求[2]。

为了提高卫星预报精度,国内外学者提出了多种卫星钟预报的模型和方法,常见的卫星钟预报模型有:多项式预报模型、灰色模型、求和自回归滑动平均模型等[3-7]。郑作亚等对不同预报模型的预报精度进行了对比分析[3];黄观文等利用频谱分析的方法,对钟差序列的周期项进行建模和预报,并取得了较高的预报精度[4];范旭亮等基于ARIMA模型对卫星钟差的短期预报性能进行了分析[5]。尽管国内外学者进行了大量的研究工作,但仍然存在预报算法难以克服粗差、相位跳变等数据异常、预报模型多样化但普适性不强、预报模型没有充分结合原子钟的物理特性等诸多问题,上述问题将极大程度地制约卫星导航系统的服务性能。因此,研究高精度的卫星钟差预报算法,进一步提高卫星钟

差的预报精度和适应性具有重要的意义。

本文在多项式预报模型的基础上,提出了一种改进的卫星钟差预报方法。先详细阐述了其相关理论及实现方法,然后结合算例,利用IGS实测的钟差数据对算法的短期预报效果进行了论证。

1改进的卫星钟差预报方法

由于多项式模型基本能反映卫星钟钟速和钟漂的物理特性,且算法的复杂程度较低,因此,本文采用的预报模型基于多项式模型进行改进。总体而言,算法的实现方法共包含三个步骤: 1) 进行数据预处理。排除粗差、相位跳变、数据中断等异常对后续处理的影响; 2) 在多项式模型的基础上,对多项式模型的选择进行改进,并对周期项进行建模; 3 )利用AR模型对消除趋势项后的残差进行建模[8]。算法的实现流程图如图1所示。本文重点对模型的改进策略及建模方法进行阐述。

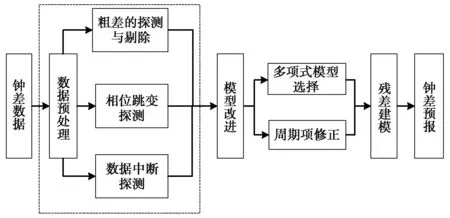
图1　改进的卫星钟差预报算法流程图

1.1多项式模型的自适应选择

对于卫星钟差预报而言,选择多项式模型的拟合阶次主要取决于卫星钟的频漂特性是否明显。由于星载原子钟的变化具有不稳定性。不同卫星会表现出不同的物理特性;对于同一颗卫星而言,在不同的时间段的物理特性也会发生变化。因此,在实际应用中,不能笼统地将其归类至单一的模型,需要利用拟合数据段的残差标准差指标进行多项式模型的自适应选择。模型的具体表达式及判断准则为

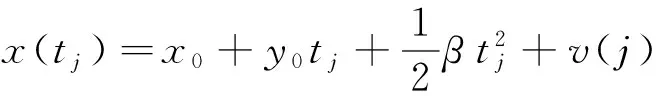
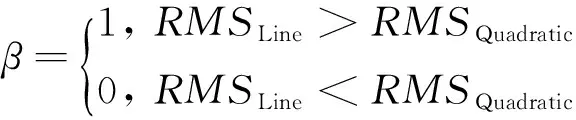
(1)

式中: x(tj)表示第j个历元的卫星钟差值; tj表示第j个历元的时刻; v(j)为该卫星钟第j个历元钟差的残差; RMSLine、RMSQuadratic分别为利用一次多项式及二次多项式拟合的残差标准差。

1.2周期项建模

利用二次多项式模型对GPS所有在轨卫星的1天数据进行拟合,其拟合的残差序列如图2所示。从图2中可以发现,几乎所有的在轨卫星的拟合残差序列均表现出不同幅度的周期特性,其周期特性将对钟差序列的拟合及后续的预报工作产生较大的负面影响。受星载原子钟的稳定度因素影响,其中G04、G10、G29的拟合残差较大。

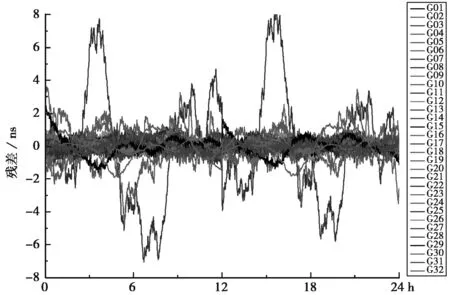
图2　GPS在轨卫星拟合残差序列图

采用频谱分析的方法对钟差序列的周期项进行建模。频谱分析主要利用数据形式呈波形的性质,通过对数据波形的幅值进行分析,对频谱图中具有较大幅值特性的显著周期项进行提取,达到消除系统误差的目的。对于钟差残差序列中的系统性误差,通过快速傅立叶级数展开式计算序列中各数值的频谱值。傅立叶变换的展开式

(2)

式中,X(k)为k时段的频谱值,x(n)为时间序列的值。其具体的理论及实现见参考文献[9-10]。在公式1的基础上,顾及周期项改正的多项式模型为

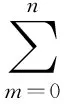
(3)

式中: x0,y0,β,Am和Bm分别为待求的模型参数,m=1,2,…n,m的大小由功率谱决定; ωk表示该卫星钟的频率变化特征参数;利用频谱分析进行周期项建模的具体步骤为

1) 采用多项式模型对观测数据进行拟合,得到其拟合残差序列vi.

2) 对拟合残差vi进行降噪处理,利用快速傅立叶变换进行处理,通过对其功率谱进行分析,确定其显著周期项,在程序设计中只选取了前6个最大的功率谱对应的频率。

3) 利用最小二乘的参数方法求解待估参数,并利用求解的参数进行后续的钟差预报。

1.3随机项建模

通过周期项建模使得钟差序列的趋势项得到较大幅度的削弱,利用AR模型对扣除多项式项及周期项后的残差v(j)进行建模。AR模型,即自回归模型,由ARIMA模型简化而来,使用该模型的一个重要前提是需要分析的时间序列是平稳的。在实际应用中,通常通过差分的方法消除数据的趋势项,从而满足模型对数据平稳性的要求。基于差分处理的ARIMA模型通常记为{Xt}～ARIMA(p,d,q)。其中,{Xt}为时间序列,p,q为模型阶数,d为差分的次数。当d为0时,其数学表达式为

Xt=φ1Xt-1+φ2Xt-2+…+φpXt-p-

θ1at-1-θ2at-2-…-θqat-q+at,

(4)

式中: φ,θ为待估参数; {at}为白噪声序列,当p,q分别为0时,模型可相应地变化为MA模型和AR模型。

为了确定更为准确的模型参数,可通过AIC准则确定模型参数,对于AR模型而言,其AIC判别函数

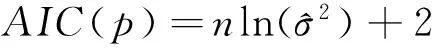
(5)

2试验和结果

本文所提出的钟差模型的预报精度,利用IGS采样率为30 s的精密钟差数据进行试验分析。采用的数据的时段为2015年3月1日至3月14日,共两周的数据,并以IGS精密钟差值作为基准,计算预报钟差与钟差基准值的残差和均方根误差(RMS),并以此作为评估依据,评估卫星钟差的预报精度。由于G26卫星在采用的数据时段内未提供服务,因此,本文及后续实验中未涉及对该颗卫星的结果分析。

为了分析改进方法利用不同拟合时长的预报精度,试验分别采用6 h、12 h、18 h和24 h的数据作为历史数据进行数据拟合,表1～表3分别示出了不同类型的卫星利用不同模型预报的均方根误差。其中BLOCK IIA卫星采用一次多项式模型的预报结果与之对比,其余卫星采用二次多项式模型进行对比分析[11-12]。表中的预报精度为利用2周数据计算的平均统计结果。

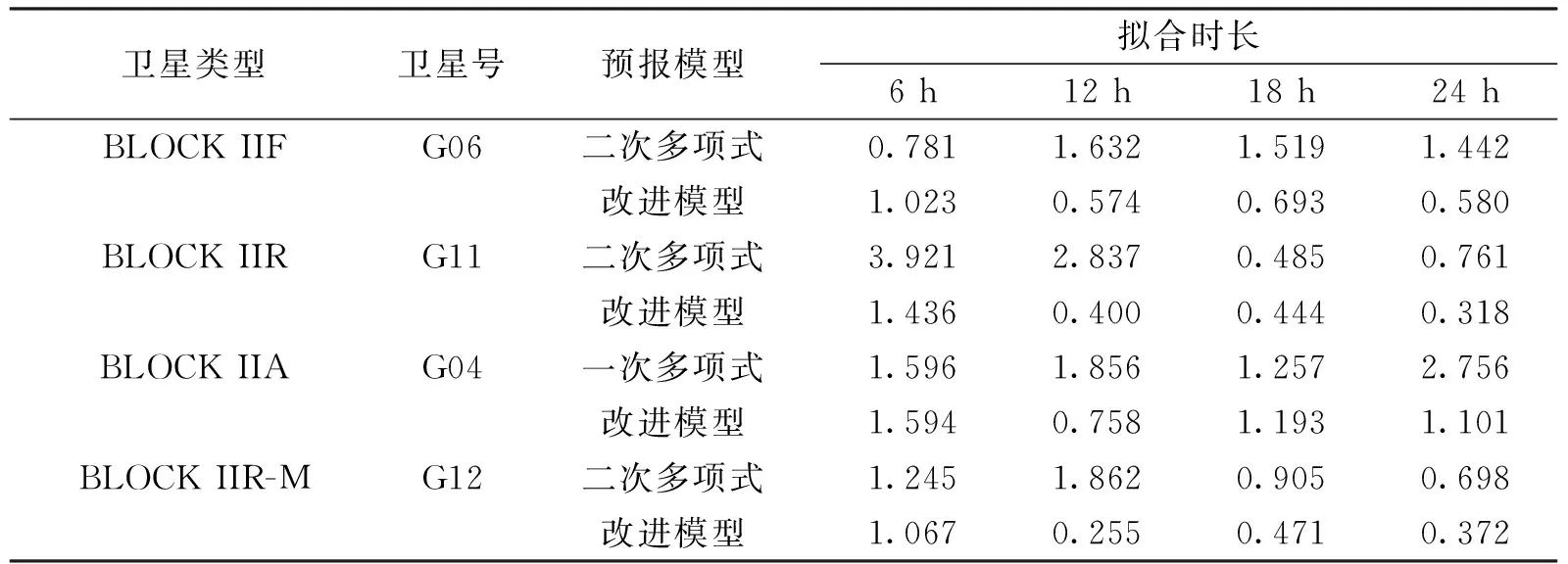
表1　不同类型卫星6 h预报精度(单位:ns)

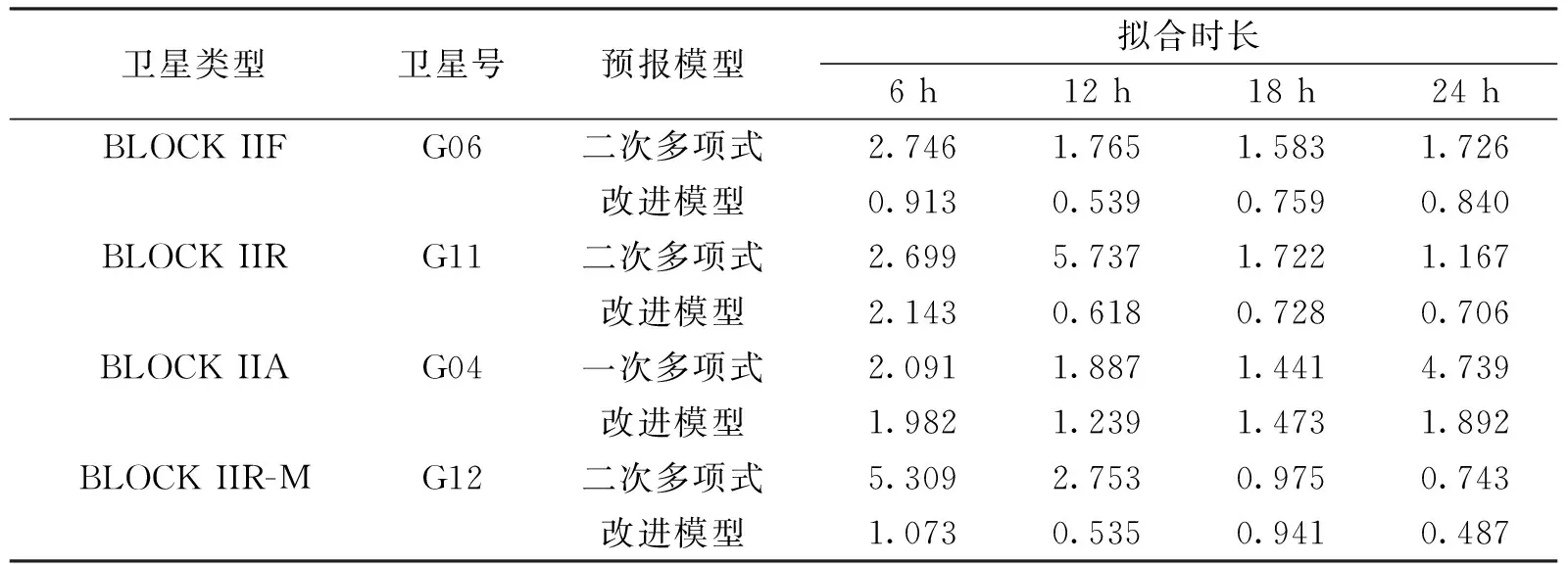
表2　不同类型卫星12 h预报精度(单位:ns)

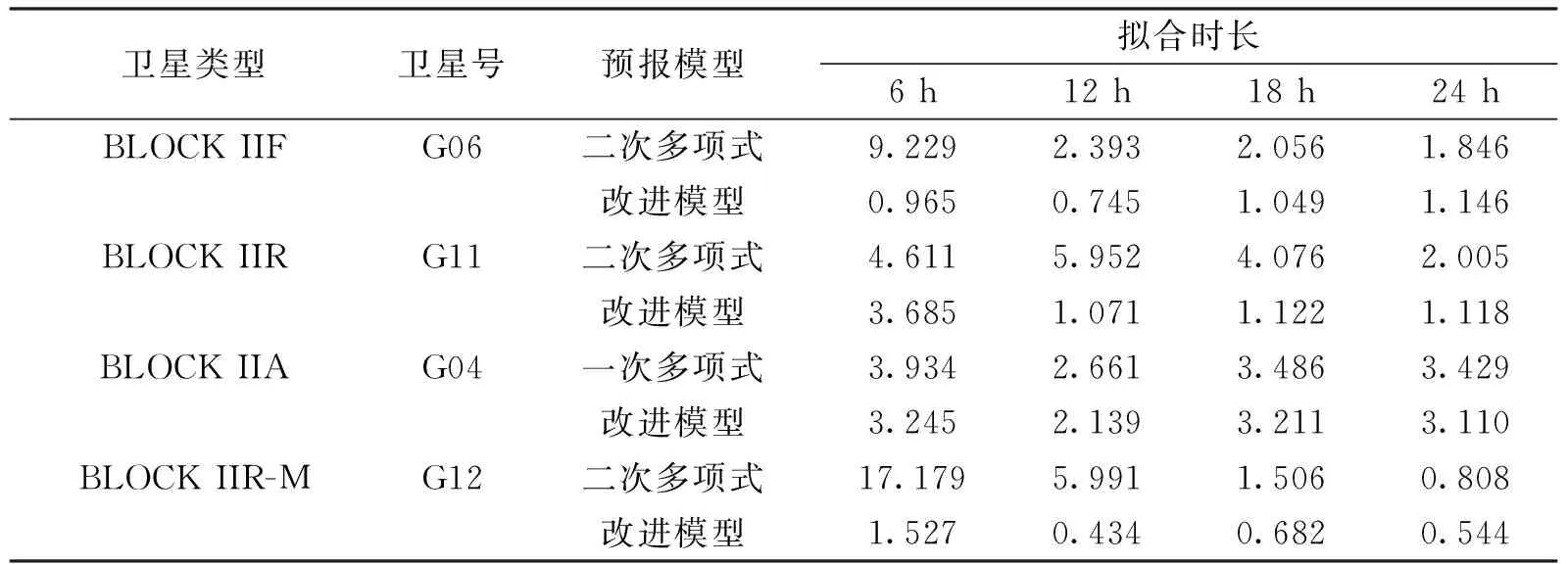
表3　不同类型卫星24 h预报精度(单位:ns)

从表1～表3中可以得到,总体而言,采用改进的预报算法的预报精度优于多项式模型,能够较为显著地提高不同类型卫星钟差的预报精度。改进算法的卫星钟预报6 h预报精度总体优于1 ns,24 h预报精度优于2 ns.

从数据拟合长度与预报精度的关系方面分析,并非拟合弧段越长,预报的精度越高。其原因可归结为拟合时段距离预测时段越远,其对预报的相关性越弱。但当采用的拟合数据量较少时,由于对少量数据拟合并不能完全反映星载原子钟物理特性的变化规律,因此预报精度较低。通过表中数据可以得到看出,当拟合弧段为6 h时,采用改进模型的预报精度明显低于采用更长拟合弧段的预报精度;当拟合弧段为12 h时,改进的预报模型能够达到较优的预报效果,当拟合数据量继续增多时,预报精度稍有降低,但变化并不显著。

为了更加直观地分析不同星载原子钟的预报效果,利用2015年3月13日的精密钟差数据进行拟合并预报后续24 h的卫星钟差。对不同类型星载原子钟的预报钟差与IGS钟差基准的残差进行统计,其预报残差随时间序列的变化关系如图3～图6所示。

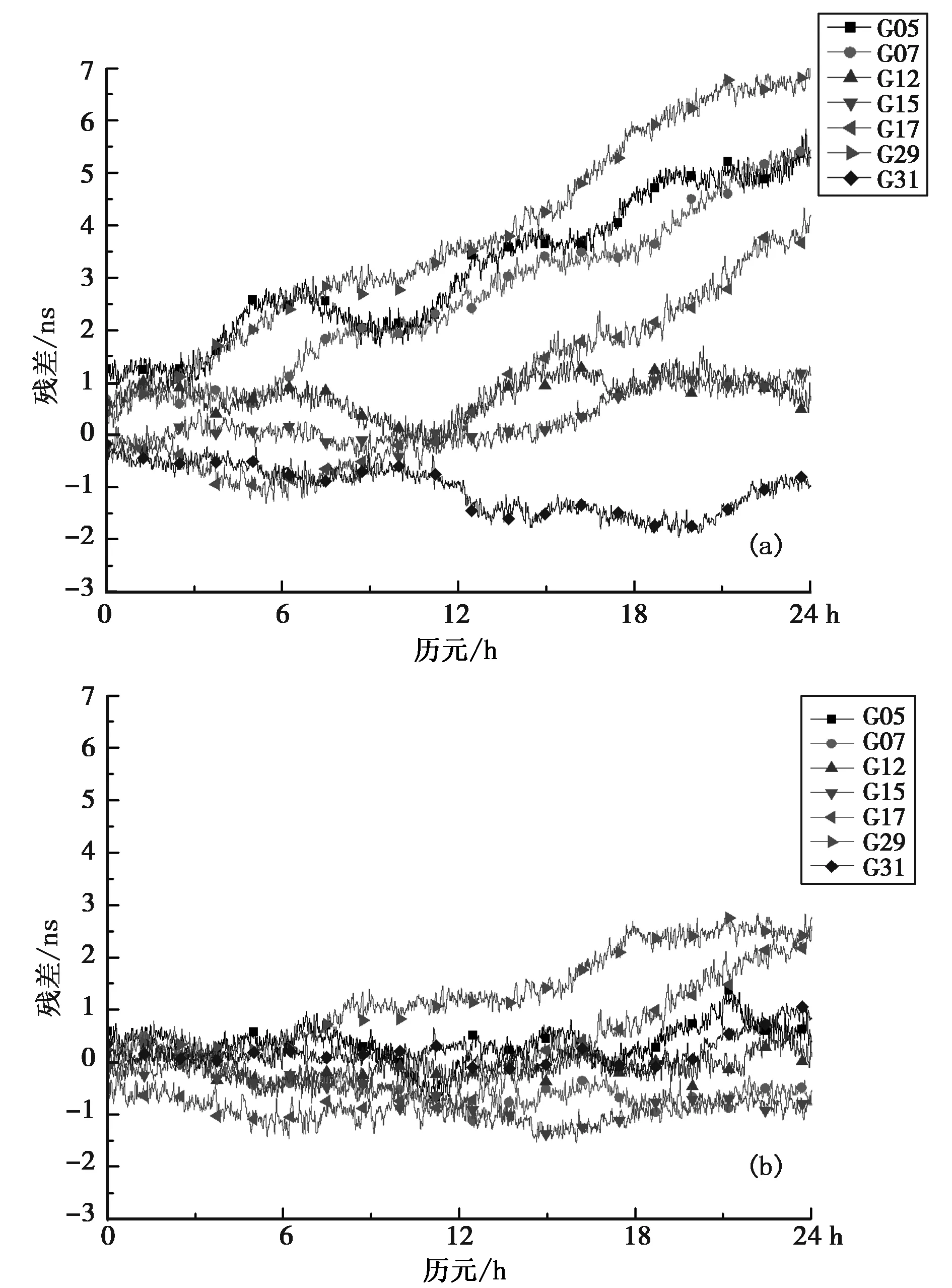
图4　BLOCK IIR-M在轨卫星预报残差序列 　　　(a) 预报模型； (b)改进的预报模型

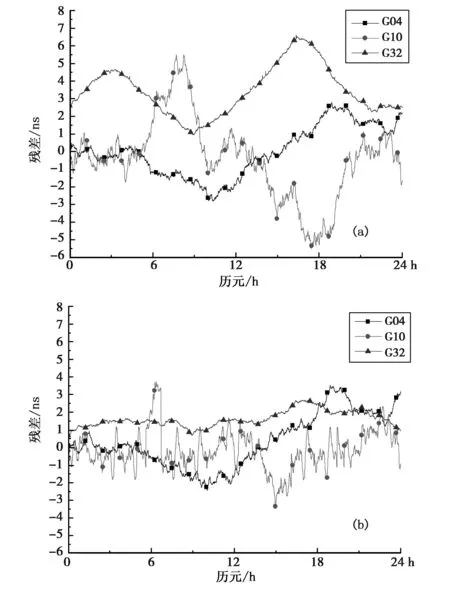
图5　BLOCK IIA在轨卫星预报残差序列 　　　(a) 预报模型； (b)改进的预报模型

图6　BLOCK IIR在轨卫星预报残差序列 　　　(a) 预报模型； (b)改进的预报模型

从图3～图6中可以得到,卫星钟差的预报精度与星载原子钟的稳定度相关,星载原子钟的稳定度越差,其预报的精度越低。同其他类型的卫星相比,BLOCK IIA卫星的预报精度最低,且预报序列呈现不规则的变化特性。由于改进的模型充分对周期项、随机项进行了建模,同多项式模型相比,改进模型的误差积累的程度有较大幅度的降低,对于稳定度较差的卫星预报的改进效果尤为显著。

3结束语

本文在多项式模型研究的基础上,提出了一种改进的卫星钟差预报方法,该模型充分考虑了星载原子钟的物理特性,并重点对多项式模型的选择、周期项修正、残差随机项修正等方面进行了改进。试验表明,改进的钟差预报模型能够显著地提高短期钟差的预报精度,对于稳定度较差的卫星的预报效果尤为显著。改进算法的卫星钟预报6 h预报精度总体优于1 ns,24 h预报精度优于2 ns.在实际应用中,可依据具体情况对模型进行扩充或简化。

文中仅研究了改进算法对GPS卫星的短期预报效果。在后续工作中,探索卫星钟差的中长期变化规律,并将算法应用于BDS卫星钟差的预报工作,是下一步的研究重点。

参考文献

[1] IGS. IGS产品[EB/OL].http://igsws.unavco.org/components/prods.html.

[2] 付文举.GNSS在轨卫星钟特性分析及钟差预报研究[D].西安:长安大学,2014.

[3] 郑作亚,卢秀山.几种GPS卫星钟差预报方法比较及精度分析[J].山东科技大学学报·自然科学版,2008,27(4):6-11.

[4] 黄观文.基于频谱分析的IGS精密星历卫星钟差精度分析研究[J]. 武汉大学学报·信息科学版,2008,33(5):497-499.

[5] 范旭亮,王晓红，张显云，等.基于ARIMA模型的卫星钟差短期预报研究[J].测绘与空间地理信息,2015,38(1):105-110.

[6] 崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报·信息科学版,2005, 30(5):447-450.

[7] 郑作亚,党亚民，卢秀山，等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J].天文学报，2010,51(1):95-102.

[8] 唐桂芬,许雪晴，曹纪东，等。基于通用钟差模型的北斗钟预报精度分析[J].中国科学:物理学 力学 天文学，2015,45(7):1-6.

[9] GREENGARD L,LEE J. Accelerating the nonuniform fast Fourier transform[J].Siam Review,2004, 46(3):443-454.

[10]LEE J-Y,GREENGARF L. The type 3 nonuniform FFT and its application[J].Journal of Computational Physics, 2005,206(1):1-5.

[11]HUANG Guanwen, ZHANG Qin,XU Guuochang,etal. Real-time clock offset prediction with an improved model[J].GPS Solutions,2014,18(1):95-104.

[12]IGS.IGS_CB分析中心[EB/OL].http://igscb.jpl.nasa.gov/pipermail/igsmail/2000/003036.html.

马卓希(1991-),男,硕士生,主要从事GNSS精密钟差解算及其预报方面的研究。

杨力(1965-),男,博士,教授,主要从事卫星导航定位等教学研究。

贾小林(1972-),男,博士,研究员,主要从事导航卫星定轨方面的研究。

赵海山(1991-),男,硕士生,主要从事GNSS理论与数据处理方面的研究。

The Optimization Method for the Satellite Clock Error Prediction Based on Polynomial Model

MA Zhuoxi1,YANG Li1,JIA Xiaolin2,ZHAO Haishan1

(1.InstituteofNavigationandSpaceTargetEngineering,InformationEngineeringUniversity,Zhengzhou450001,China;2.Xi'anInstituteofSurveyingandmapping,Xi'an710054,China)

Abstract: According to the physical characteristics of satellite clock, this paper adopts a universal clock offset model based on polynomial prediction model. Multiple improvements have been verified,which contains the self-adaptive selection of polynomial model, modeling for periodic term and modeling for the residual term. Firstly, the adaptive selection of polynomial fitting model is judged by the standard deviation of residual. Then the periodical term of clock offset is modeled using spectrum analysis. Finally the stochastic model after removing the periodical term is constructed using AR model. The experiment results show that the proposed model can greatly improve the short-term prediction accuracy, especially for less stable satellite clock. The overall accuracy of 6 h prediction can be better than 1 ns and 24 h prediction accuracy better than 2 ns.

Keywords:GPS; satellite atomic clock; Polynomial model; clock offset prediction

doi:10.13442/j.gnss.1008-9268.2016.02.005

收稿日期：2015-11-02

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2016)02-0027-06

作者简介

联系人： 马卓希 E-mail: mzhx-1991@163.com