部分模糊度固定技术在动态精密单点定位中的应用

丁赫,孙付平,刘帅,门葆红,刘婧

(信息工程大学 导航与空天目标工程学院,郑州 450001)

部分模糊度固定技术在动态精密单点定位中的应用

丁赫,孙付平,刘帅,门葆红,刘婧

(信息工程大学 导航与空天目标工程学院,郑州 450001)

摘要：在精密单点定位中,模糊度固定是一个难点问题,而由于窄巷模糊度波长较短,对其进行固定更为困难。本文采用逐级模糊度固定的策略,利用整数相位钟法实现了GPS PPP模糊度固定。在此基础上,改进传统LAMADA方法所采用的全部模糊度固定(FAF)技术,采取了一种部分模糊度固定(PAF)技术,并将其应用到窄巷模糊度固定中。该方法综合考虑位置精度因子、连续观测历元数、模糊度精度因子和Ratio值等因素,在兼顾模糊度固定可靠性的同时去提升模糊度固定率。通过4个MGEX站的实测数据进行动态PPP实验,结果表明:相较于FAF方法,PAF方法有效的提高了模糊度的固定率并进一步改善了定位精度;在观测条件较少或者残余误差较大时,部分模糊度固定可减少首次固定的时间。

关键词：精密单点定位;整数相位钟法;部分模糊度固定;全部模糊度固定;模糊度固定率;首次固定时间

0引言

模糊度固定是提升精密单点定位性能的有效方法,也是精密单点定位中的难点问题。为解决该问题,国内外众多研究学者做了大量研究[1-6]。然而,在GPS PPP中,由于周跳、残余误差和测量噪声等因素的影响,全部模糊度固定(FAF)往往难以实现。文献[7]首次将部分模糊度固定(PAF)应用到PPP中,并进行了单站静态实验和精度评估;文献[8]以模糊度精度因子为选取标准实现了窄巷模糊度的部分固定,并对Ratio、成功率的阈值选定问题进行了研究;文献[9]则在联合使用Ratio值和成功率进行部分模糊度固定,但同样只进行了静态PPP实验。

目前在精密单点定位中,大部分PAF是在静态模式下进行的,在动态PPP中的应用研究相对较少,文献[10]结合高度角、模糊度标准差作为模糊度子集的选取标准,以Ratio值和固定成功率作为模糊度正确固定的依据,并进行了大量的静态和

动态实验分析,取得了很好的效果。

本文则采用一种新的PAF方法,并将其应用到动态PPP中,利用MGEX测站的实测数据进行相关实验,将PAF方法和FAF方法在首次固定时间、模糊度固定率、定位精度等方面进行了比较分析。本文安排如下:首先论述了基于整数相位钟法的逐级模糊度固定策略;然后详细论述了本文所提出的部分模糊度固定技术;最后通过动态PPP实验对该方法的作用进行了论证分析。

1模型与方法

1.1基于整数相位钟法的逐级模糊度固定策略

在精密单点定位中,GPS消电离层组合观测方程为

(1)

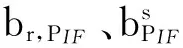
整数相位钟法PPP模糊度固定的重要思想是将伪距接收机钟差和载波相位接收机钟差进行区分[11]。基于该思想,GPS消电离层组合观测方程可表示为

(2)

(3)

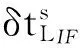
(4)

其中,p代表基准星,q代表流动星:

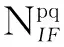
(5)

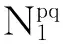
然而,在模糊度固定过程中,宽巷模糊度波长较长,易于固定;而窄巷模糊度由于波长较短,在通过LAMADA算法解算后,往往会出现无法通过Ratio值检验的情况,进而导致消电离层模糊度固定的失败。因此,PPP模糊度固定成功与否的关键在于窄巷模糊度的固定。为此,改进了传统LAMADA方法,将部分模糊度固定技术应用于单差窄巷模糊度固定。

1.2部分模糊度固定方法

某些情况下,由于周跳、残余误差和测量噪声等因素的影响,无法将全部模糊度固定,而通过固定其中一部分模糊度同样可以起到改善定位精度的作用。方差作为衡量观测值精度高低的指标,也体现了模糊度浮点解与固定解的接近程度。方差较小的模糊度浮点解,意味着更接近固定解,正确固定的可能性越大[14];Ratio值在一定程度上反映了模糊度固定可靠性,其大小可作为模糊度固定正确与否的参考标准;而浮点解PPP的位置精度也可以作为模糊度能否可靠固定的参考依据[15],此外,获得精度较好的浮点模糊度需要一定的收敛时间,过低高度角和周跳均会影响模糊度的精度,因此,在满足截止高度角的前提下,对连续观测20个历元以上的卫星组成的单差窄巷模糊度进行固定。综上所述,在部分模糊度固定中,为在提高模糊度固定率的同时,保证模糊度固定的可靠性,本文将模糊度方差因子作为模糊度子集的选取依据,将三维位置方差因子的平方根σ3D和连续观测历元数作为模糊度固定与否的依据;将Ratio值作为模糊度固定正确与否的检验标准(本文选取的σ3D和Ratio的阈值分别为0.08 cm和2.0)。在动态PPP中,其具体处理策略如图1所示(其中N代表剩余单差窄巷模糊度数量):

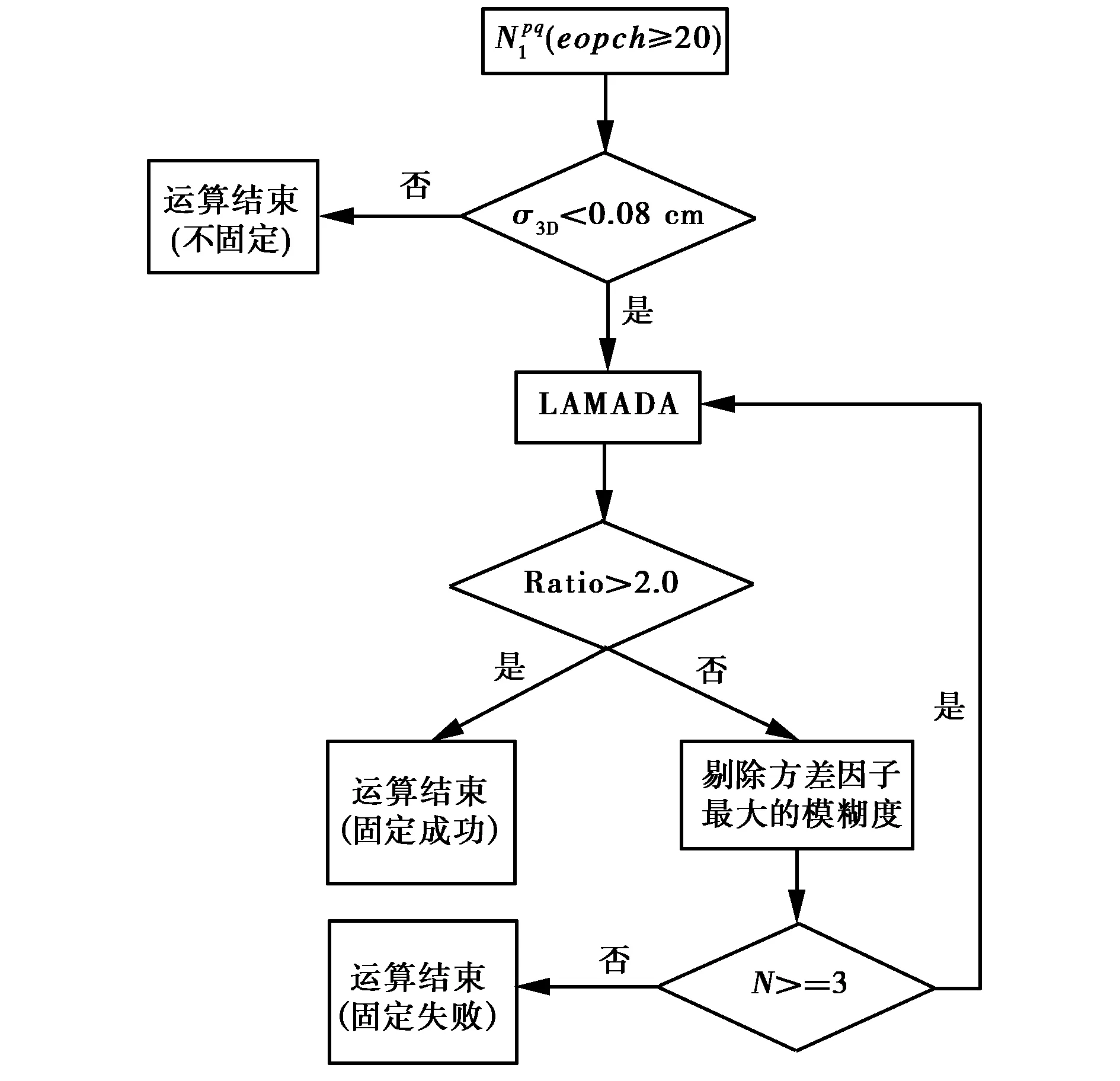
图1　部分模糊度固定流程图

具体步骤如下:

1) 首先,选取连续观测20个历元以上的卫星组成单差窄巷模糊度,判定σ3D是否小于阈值,若不是,则运算结束,不固定模糊度;若是,则进行步骤2);

2) 利用LAMADA方法对全部单差窄巷模糊度进行固定,以Ratio值大小判定是否固定成功,若大于2.0,则固定成功,结束运算;若不大于2.0,则进行步骤3);

3) 以模糊度方差因子作为参考标准,剔除方差因子最大的单差窄巷模糊度,判断余下的单差模糊度数量是否小于3,如果小于3,则结束运算,固定失败;如果大于3,则进行步骤4);

4) 对余下的单差窄巷模糊度利用LAMADA方法进行固定,以Ratio值大小判定是否固定成功,若成功,则结束运算,若失败,则再次进行步骤3)。

通过步骤3)、步骤4)循环的方式固定模糊度,直至运算结束为止。这种方法在保证模糊度固定成功的前提下,尽可能多的固定单差窄巷模糊度。

2数据与算例分析

2.1实验数据与方案

为验证本文所提出的部分模糊度固定方法,选取DJIG、DYNG、GMSD、ONS1这4个MGEX跟踪站2015年DOY203天2:00-22:00的观测数据进行动态定位实验。对于精密产品,采用CNES分析中心提供的30 s精密钟差和15 min的精密星历。

实验将每份观测数据以4 h划分为一个观测时段,在动态模式下分别进行浮点解PPP、全部模糊度固定(FAF)的PPP和采用PAF方法的PPP 3种方式的解算。将解算结果与参考真值做差,获得E、N、U三个方向的坐标偏差。其中,“参考真值”为CNES发布的的单天解。

2.2实验结果分析

以DYNG站为例,给出该站在首个观测时段内三种解算方式的位置偏差图，如图2所示，以及两种模糊度固定方法的Ratio值变化图，如图3所示。结合图2和图3可以看出,在观测时段内,浮点解PPP收敛时间较长,E、N、U三个方向的位置偏差在4:30左右才逐渐稳定收敛至10 cm以内;采用FAF方法的PPP固定解,在3:04:30首次实现模糊度固定,E、N、U三个方向的位置偏差迅速降至厘米级,且在之后的大部分历元实现了模糊度固定,保持较好的位置精度,但是在4:30左右,模糊度固定失败,位置偏差变大;而采用PAF方法的PPP固定解,则在2:53:30首次实现了模糊度固定,并在之后的所有历元均实现了模糊度固定,始终保持较高的位置精度。

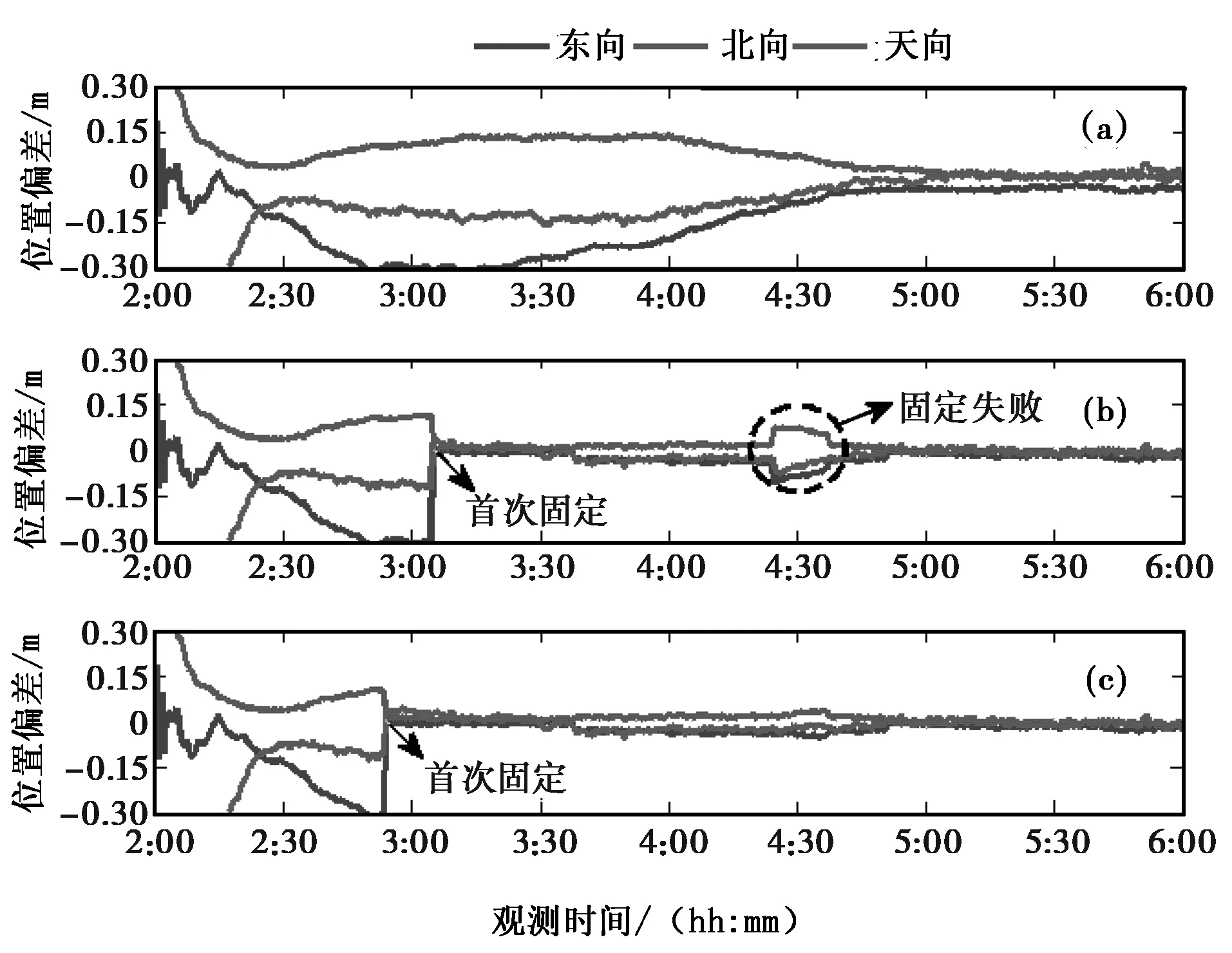
图2　DYNG站第一时段动态PPP位置误差(a) PPP浮点解; (b) 传统PPP固定解；(c) 部分模糊度固定的PPP固定解

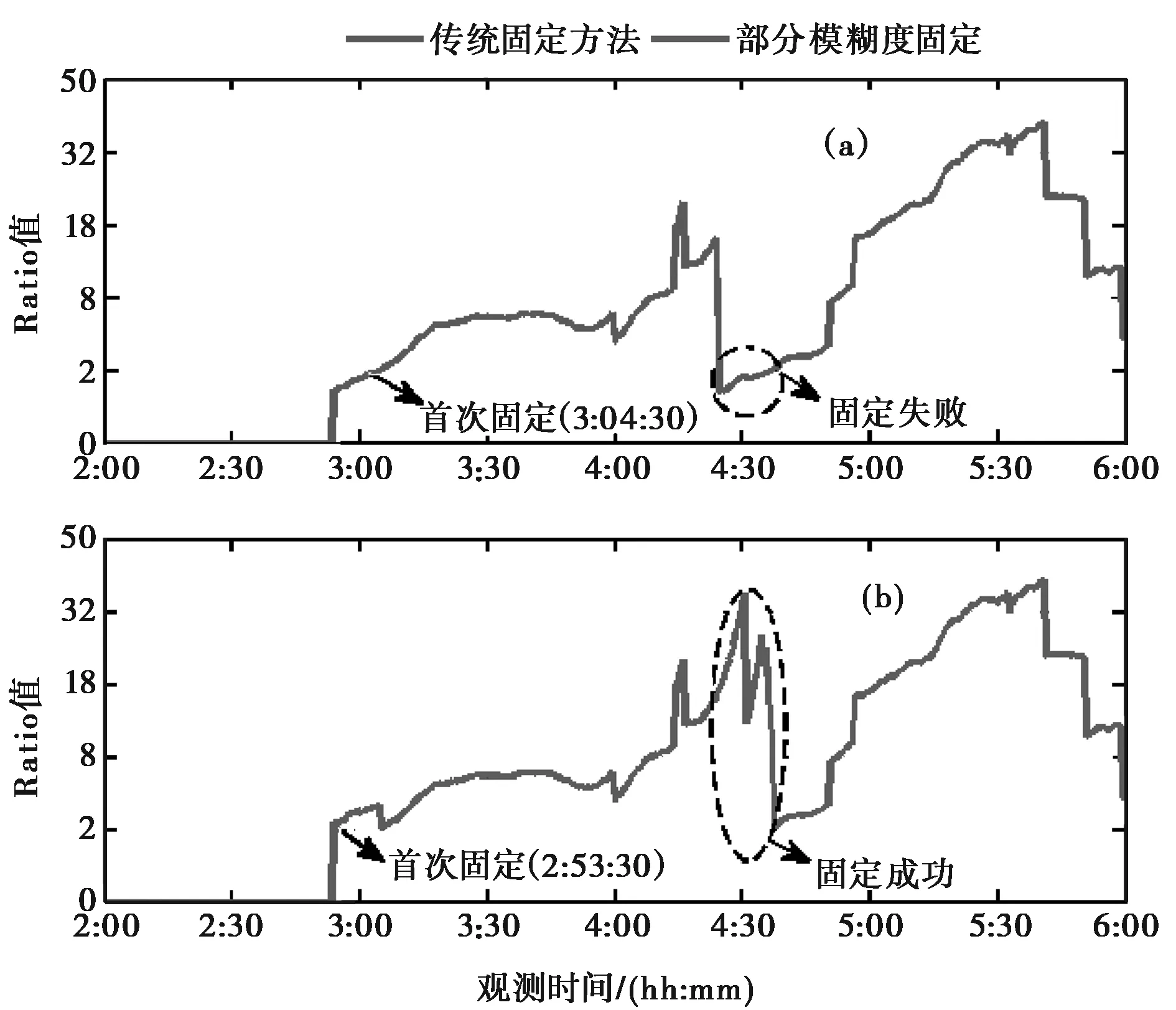
图3　DYNG站第一时段Ratio值变化图 (a) 传统固定方法; (b) 部分模糊度固定

需要指出的是,在定位解算的前期,σ3D大于阈值(0.08 cm),没有进行单差窄巷模糊度固定,所以图3所示中前期阶段Ratio值为默认值0.

为评定部分模糊度固定的定位性能,本文再做以下具体统计分析。

首先是模糊度首次固定时间,图4示出4个测站20个观测时段的首次固定时间(TTFF),依次为DJIG、DYNG、GMSD、ONS1.可以看出,在大部分观测时段内,两种模糊度固定方法的首次固定时间是相同的,而在部分观测时段,PAF方法的首次固定时间较FAF方法有所减少,从图中不难发现,这一类观测时段的首次固定时间普遍比较长。这主要是因为模糊度的固定很大程度上依赖于浮点解模糊度的精度,当观测信息较少或者残余误差较大时,浮点解很难收敛较慢,浮点模糊度精度不高,全部模糊度固定难以实现。而采用PAF方法,则可以剔除一部分精度较差的浮点模糊度,对另一部分精度较好的模糊度实现固定,进而达到缩短首次固定时间的效果。但是就平均意义而言,PAF方法起到了缩短首次固定时间的作用。表1为动态模式下两种模糊度固定方法的首次固定时间具体统计信息,其中,FAF方法的平均首次固定时间为49.3 min,采用PAF方法后,首次固定时间减少为45.6 min,相较于FAF方法,略有减少。

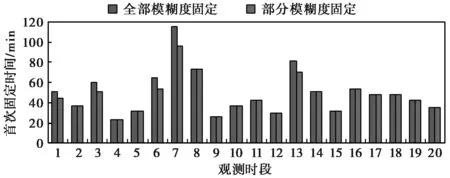
图4　20个观测时段的首次固定时间

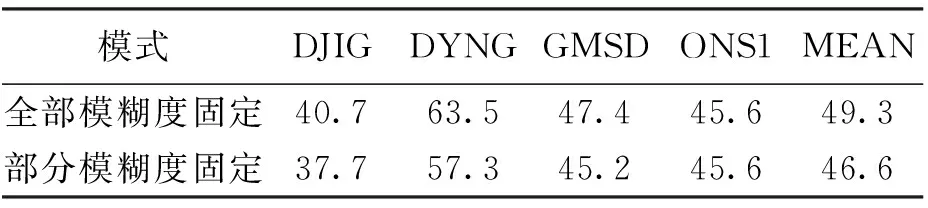
模式DJIGDYNGGMSDONS1MEAN全部模糊度固定40.763.547.445.649.3部分模糊度固定37.757.345.245.646.6

其次,将PPP模糊度固定率进行了统计,如图5所示,从图中可以看出,在所有观测时段中,PAF的模糊度固定率较FAF的模糊度固定率均有不同程度的提高。各测站模糊度固定率的具体统计信息如表2所示。

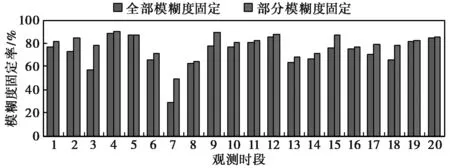
图5　20个观测时段的模糊度固定率

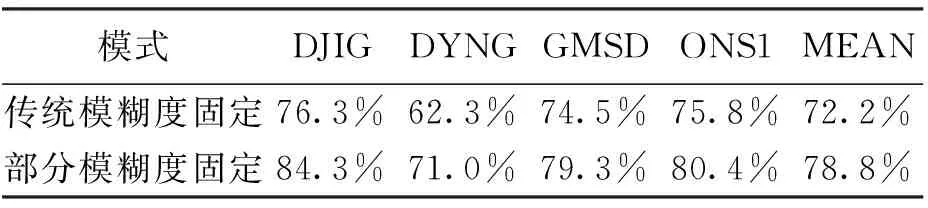
模式DJIGDYNGGMSDONS1MEAN传统模糊度固定76.3%62.3%74.5%75.8%72.2%部分模糊度固定84.3%71.0%79.3%80.4%78.8%

从表中可以看出,在观测时长为4 h的情况下,FAF的平均固定率为72.2%,而PAF方法的平均固定率为78.8%,提高了近7个百分点。这主要是由于两方面原因,一方面在观测信息较少或者残余误差较大的情况下,PAF方法减少了首次固定时间,进而使FAF方法首次固定之前的部分历元的模糊度得以固定;另一方面,FAF方法模糊度首次固定之后的部分历元未能成功进行模糊度固定,采用PAF方法,剔除精度较差的浮点模糊度之后,使这部分历元实现了模糊度固定。

最后,选取每个观测时段最后2小时的定位结果进行统计分析,表3示出了各测站位置误差的RMS具体统计结果。

从表中可以看出,固定解的位置精度明显好于浮点解。其中,其平均统计结果显示:相较于PPP浮点解,采用FAF方法的PPP固定解E、N、U三个方向的位置精度分别改进了38.9%、26.1%、33.5%;而采用PAF方法的PPP固定解的位置精度又有了进一步的提升,E、N、U三个方向分别改进了49.6%、34.6%、33.5%.这主要是由于PAF方法提高了模糊度固定率,进而使在FAF方法中未能成功固定部分浮点解获得了精度更高的固定解,进而提高了统计样本整体的精度。

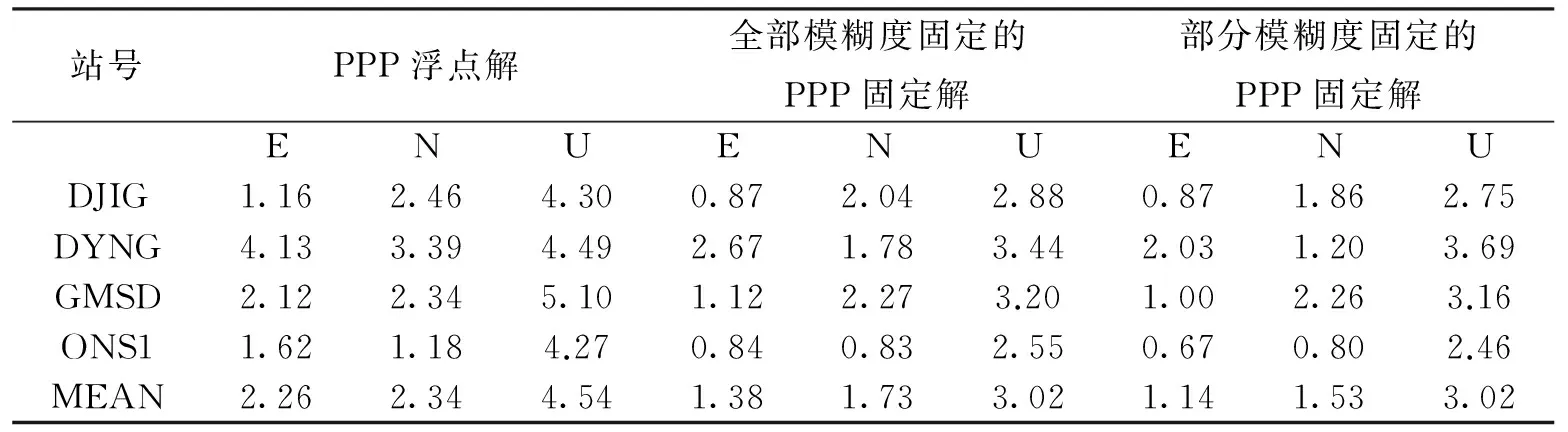
表3　各站动态PPP定位偏差RMS统计(单位：cm)

3结束语

本文采用逐级模糊度固定的策略,利用整数相位钟法实现了GPS PPP模糊度固定。在此基础上,改进传统LAMADA方法,采用一种部分模糊度固定技术,并将其应用到动态PPP中。通过4个MGEX站的实测数据进行实验,结果表明:①在观测信息较少或残余误差较大的情况下,PAF方法可有效的减少模糊度首次固定时间; ②在观测时长为4 h的情况下,传统模糊度固定方法的平均固定率为72.2%,而PAF方法的平均固定率为78.8%,提升了近7个百分点。③PPP固定解的位置精度明显好于浮点解,采用FAF方法的固定解PPP,E、N、U三个方向分别改进了38.9%、26.1%、33.5%,而采用PAF方法的PPP固定解的位置精度又有了进一步的提升,E、N、U三个方向分别改进了49.6%、34.6%、33.5%.

综上所述,在动态PPP中,相较于全部模糊度固定,部分模糊度固定技术可以提高模糊度固定率、改善定位精度,此外,还可以在观测信息较少或残余误差较大的情况下缩短手段首次固定时间,是一种有效的模糊度固定的质量控制方法。

参考文献

[1] LAURICHESSE D, MERCIER F, BERTHIAS J P,etal. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination[J].Navigation: Journal of the Institute of Navigation, 2009, 56(2): 135-149.

[2] GE M,GENDT G,ROTHACHER M,etal.Resolution of GPS acrrier-phase ambiguities in precise point positioning(PPP) with daily observation[J].Journal of Geodesy,2008,82(7):389-339.

[3] COLLINS P,BISNATH S.LAHAVE F,etal.Undifferenced GPS ambiguity using the decoupled clock model and ambiguity datum fixing[J].Navigation,2010,57(2):123-135.

[4] ZHANG X, LI P, GUO F. Ambiguity resolution in precise point positioning with hourly data for global single receiver[J]. Space Resraech, 2013(51):153-161.

[5] LOYER S, PEROSANZ F, MERCIER F,etal. Zero-difference GPS ambiguity resolution at CNES-CLS IGS Analysis Center[J]. Journal of Geodesy, 2012(86): 991-1003.

[6] SHI J.Precise point positioning integer ambiguity resolution with decoupled clocks[D].Calgary, Alberta:Department of Geomatics Engineering,2012.

[7] VERHAGEN S, TEUNISSEN P J G,elal. GNSS ambiguity resolution: Which subset to fix[C].// In Proceedings of the 2011 IGNSS Symposium, International Global Navigation Satellite Systems Society, Sydney, Australia, 15-17 November 2011:1-15.

[8] SHI J, GAO Y. A fast integer ambiguity resolution method for PPP.[C].// In Proceedings of the ION GNSS, Nashville, TN, USA, 17-21 September, 2012:3728-3734.

[9] 赵兴旺 张翠英.精密单点定位部分模糊度固定方法[J].北京：中国空间科学术,2013,1:37-44.

[10]LI P,ZHANG X.Precise point positioning with partial ambiguity fixing[J].Sensors,2015(15): 13627-13643.

[11]刘帅,孙付平,郝万亮,等.整数相位钟法精密单点定位模糊度固定模型及效果分析[J].测绘学报,2014,43(12):1230-1237.

[12]TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J]. Journal of Geodesy, 1995, 70(1-2): 65-82

[13]TEUNISSEN P J G. Success probability of integer GPS ambiguity rounding and bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606-612.

[14]赵兴旺,王庆,潘树国.LAMBDA算法的部分模糊度固定及性能分析[J].中国惯性技术学报,2015,18(6):665-669.

[15]LOYERS, PEROSANZ F, MERCIERF,etal. Zero-difference GPS ambiguity resolution at CNES-CLSIGS analysis center[J].Journal of Geodesy, 2012, 86(11): 991-1003.

丁赫(1990-),男,吉林通化人,硕士，研究方向为GNSS精密单点定位。

孙付平(1964-),男,河南长葛人,教授,主要从事惯性导航、卫星导航、组合导航等方向的教学与研究工作。

刘帅(1986-),男,山东枣庄人,博士,研究方向为精密单点定位及其与惯性导航系统的组合。

门葆红(1966-),女,河南洛阳人,副教授,硕士,主要从事测绘科研和教学工作。

刘婧(1986-),女,河南长葛人,讲师,主要从事测绘科研和教学工作。

The Application of Partial Ambiguity Fixing to Kinematic PPP

DING He,SUN Fuping,LIU Shuai,MEN Baohong,LIU Jing

(InstituteofNavigationandSpaceTargetEngineering,InformationEngineeringUniversity,Zhengzhou450001,China)

Abstract: Ambiguity fixing is a thorny issue in precise point positioning, and the narrow lane ambiguity is more difficult to fix because of the short wavelength. This paper realized the ambiguity fixing by use of the inter phase clock method which employs a cascaded ambiguity fixing strategy. On this basis, we improve the full ambiguity fixing(FAF) method which is used in traditional LAMADA algorithm and a partial ambiguity fixing(PAF) model is put forward to fix the narrow lane ambiguity. This method takes into consideration various factor, such as position variance factor,the number of continues observation epoch,ambiguity variance factor and the value of ratio, gives consideration to both the reliability of ambiguity fixing and improving the fixing rate. Four MGEX stations are used to kinematic PPP test. The results show that: Compared with traditional FAF method, PAF method increases ambiguity fixing rate effectively and improves positioning accuracy. In addition,the time to first fixed(TTFF) is reduced for less measurement information or lager residual error.

Keywords:Precise point positioning (PPP); inter phase clock method; partial ambiguity fixing(PAF); full ambiguity fixing(FAF); ambiguity fixing rate; time to first fixed(TTFF)

doi:10.13442/j.gnss.1008-9268.2016.02.006

收稿日期：2015-12-23

中图分类号：P228.4

文献标志码：A

文章编号：1008-9268(2016)02-0032-06

作者简介

资助项目: 基于空间大地测量实测数据的全球构造变化研究(编号：41374027)

联系人： 丁赫E-mail: 973515254@qq.com