关于经管类微积分教学中无穷小量与无穷大量的探讨
2016-06-22孙祥凯张付臣
孙祥凯,张付臣
(重庆工商大学 数学与统计学院,重庆 400067)
关于经管类微积分教学中无穷小量与无穷大量的探讨
孙祥凯,张付臣
(重庆工商大学数学与统计学院,重庆400067)
[摘要]文章借助反例进一步讲解了经管类微积分课程教学中无穷小量、无穷大量以及无界变量之间的关系和性质。教学实践证明,在微积分教学中恰当地使用反例,能够帮助学生加强对相关知识点的理解。
[关键词]无穷小量;无穷大量;无界变量;教学改革
[DOI]10.13939/j.cnki.zgsc.2016.02.155
1引言
微积分课程是经济管理类专业本科生的专业基础课。而无穷小量与无穷大量又是微积分课程中的两类非常重要的概念。[1-3]因此,经济管理类专业本科生如果能够灵活运用无穷小量以及无穷大量的相关性质以及它们之间的关系,对后续一元函数和数列的极限计算,一元函数的连续性,导数以及可微性的证明和求解都会有很大帮助。
笔者近些年对经济管理类专业本科生的教学实践发现,许多教材在对无穷小量以及无穷大量的讲解中,仅仅对无穷小量的各种性质进行展开讨论,而关于无穷大量的性质却一笔带过,如李霄民与夏莉等出版的《微积分》上册。[1]不仅如此,笔者发现许多教材在讲解无穷小量以及无穷大量之间的关系与性质时,特别是关于无穷大量的性质,不仅没有适当的证明,而且也没有足够的反例来解释相关问题。因此许多文献补充了相关性质,并列举了适当的反例。然而,笔者发现许多反例晦涩难懂,不利于像文科类学生居多的工商类院校学生的理解。
基于上述问题,笔者将通过中学中一些常见的简单易懂的例子出发,对无穷小量以及无穷大量的学习中易产生误解的性质与关系进行了总结和归纳,进一步认识二者之间的关系和性质,解决学生学习中的迷茫和疑惑,从而激发学生学习微积分课程的兴趣。[4]
2无穷小量与无穷大量的性质反例
本文首先回顾微积分的教材中关于无穷小量的如下三个性质。[1,2]
性质1:有限个无穷小量的和与差仍为无穷小量。
性质2:有限个无穷小量的乘积仍为无穷小量。
性质3:有界变量与无穷小量的乘积仍为无穷小量。
教材中对上述几个性质有许多例子进行解释。然而如果把上述性质1和性质3中无穷小量换为无穷大量一定成立吗?回答是否定的。下面通过几个中学中常用的函数构造反例进行解释。这样不仅简单易懂,而且学生更容易接受。
命题1:有限个无穷大量的和与差不一定是无穷大量。
命题2:有界变量与无穷大量的乘积不一定为无穷大量。
总结:在数学的学习中,要学会用最简单的函数构造反例,解决相关问题,从而达到融会贯通的效果。
3无穷大量与无界变量的比较反例
在讲解无穷大量与无界变量之间的关系前,我们首先强调下关于无穷大量的几点注意事项。
注意1:需要强调的是无穷大量指的是绝对值无限增大的变量。此处与中学的有些区别。很多同学总是认为只有最终趋近正无穷的变量才是无穷大量。而最终趋近负无穷的变量则是无穷小量。这种理解显然是没有搞清楚无穷小量和无穷大量的定义。
注意2:无穷大量是一个变量,不可与绝对值很大很大的数混为一谈。同样,我们也不能认为无穷小量为很小很小的数。
在理解了无穷大量的定义后,我们对无穷大量与无界变量之间的关系进行再总结归纳,并给出几个例子进行分析。
(1)无穷大量是无界变量。
(2)无界变量不一定是无穷大量。
总结:正确理解无穷大量与无界变量之间的关系,不仅为以后学习其他知识做好铺垫,而且对培养数学思维也有着一定作用。
4无穷小量的等价代换方法求极限的应用误区
正确地利用无穷小量的等价代换方法求解某些函数的极限,不仅简化计算步骤,而且可以取得事半功倍的结果。然而笔者发现,自从讲解了无穷小量的等价代换方法后,许多学生没看清楚无穷小量的等价代换方法适用范围,就不假思索地借助该方法求解,从而导致许多计算结果的失误和错误。所以正确灵活运用无穷小量的等价代换方法就显得极为重要。笔者通过以下注意事项以及几个实例和反例将对该问题进一步的总结和阐述。
注意1:在利用无穷小量的等价代换方法求极限时首先要看清自变量的趋近过程。只有无穷小量时才可以考虑等价代换方法。如果不是无穷小量,则不能借助等价代换方法求极限。

分析:很多同学会不假思索地借助等价代换方法去求解,即
因为sinx等价于x,sin2x等价于2x,所以

显然,上述求解方法是错误的。错误之处在于,忽略自变量的趋近过程,机械套用等价代换方法。我们在前面强调过只有是无穷小量时,才可以考虑借助等价代换法。
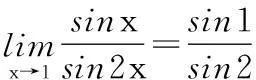
为让读者有个更加清晰的认识,下面给出一个可以借助无穷小量的等价代换方法求极限的例子。
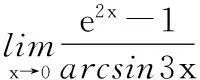
分析:当x→0时,函数e2x-1和arcsin3x均为无穷小量。因此可以借助无穷小量的等价代换方法求解。
解:因为当x→0时,e2x-1等价于2x,arcsin3x等价于3x,所以

注意2:在微积分教材中,曾强调过利用等价无穷小量代换求极限时,只能用于乘除,对于加减运算的无穷小量不能随意代换。
注意:这里说的是不能随意代换,也就是有些可以,有些不可以。许多文献对此都有很多解释,并给出了各种命题来说明等价代换所适用的范围条件等。但是这些定理如果直接拿来给经管类本科生解释,不仅不能消除他们的困惑,而且容易使他们对微积分的学习产生厌倦心理。
近些年来,笔者在给经管类本科生讲解微积分课程时发现,单独的理论讲解以及定理推导不适合工商类院校本科生。当代大学生更倾向于实例分析,即用实例来解释晦涩难懂的数学定理命题等。因此笔者将借助一个简单例子来分析上述问题。
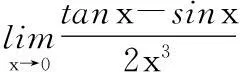
分析:很多同学会直接这样求解:当x→0时,函数tanx-sinx和2x3均为无穷小量。又知当x→0时tanx与sinx均等价于x。所以

显然上述求解方法是错误的。正确的求解释方法是先将加减转化为乘除再进行代换。虽然教材中已有很多这种例子,但为读者方便我们仍然写出详细过程。
正解:首先将加减转化为乘除,即



综上所述,无穷小量的等价代换方法是计算极限问题的一种行之有效的方法。但使用过程中要注意教材所说对于加减不能随便利用。因此若使用不当,将会适得其反。所以我们在利用无穷小量的等价代换方法时,如果遇到含有加减的无穷小量时,尽量不要直接代换,以免导致错误。
5结论
无穷小量和无穷大量在大学数学的相关问题求解中有着举足轻重的地位和作用。因此,在学习这两个概念时一定要把握好细节问题,要知其所以然,从而理解它们的深刻内涵。本文对经管类微积分课程中无穷小量、无穷大量以及无界变量之间的性质和误区进行了总结和归纳,消除了学习中可能遇到的误区,从而达到预期的学习效果。
参考文献:
[1]李霄民,夏莉等.微积分(上册)[M].北京:高等教育出版社,2012.
[2]华东师范大学教学系.数学分析(上)[M].北京:高等教育出版社,2001.
[3]张谋,魏曙光,无穷大量的性质与应用[J].高等数学研究,2013(16):5.
[4]伏红勇.工商管理类本科生经济数学应用能力培养的教学研究[J].中国市场,2014(25).
[作者简介]孙祥凯 (1984—),男,汉族,山东青州人,博士后,副教授。研究方向:最优化方法、数学教学方法。
