不同围压条件下含气致密砂岩孔裂隙形态演化试验研究
2016-06-21丁文龙孙圆辉单钰铭王濡岳
尹 帅,丁文龙,孙圆辉,单钰铭,王濡岳
(1.中国地质大学(北京)能源学院,北京100083;2.海相储层演化与油气富集机理教育部重点实验室,中国地质大学(北京),北京100083;3.页岩气资源战略评价国土资源部重点实验室,中国地质大学(北京),北京100083;4.中国石油天然气股份有限公司石油勘探开发研究院,北京100083;5.成都理工大学能源学院,四川成都610059)
不同围压条件下含气致密砂岩孔裂隙形态演化试验研究
尹帅1,2,3,丁文龙1,2,3,孙圆辉4,单钰铭5,王濡岳1,2,3
(1.中国地质大学(北京)能源学院,北京100083;2.海相储层演化与油气富集机理教育部重点实验室,中国地质大学(北京),北京100083;3.页岩气资源战略评价国土资源部重点实验室,中国地质大学(北京),北京100083;4.中国石油天然气股份有限公司石油勘探开发研究院,北京100083;5.成都理工大学能源学院,四川成都610059)
摘要:对4组深层致密砂岩样品进行不同围压条件下的声学测试,利用Biot相洽原理及微分等效介质原理对岩石裂隙密度ε及孔隙纵横比α进行了反演。将2种方法相结合探讨了不同围压条件下岩石中孔裂隙形态演化及分布规律,避免了单一方法研究的不足。研究结果表明,ε随围压增加而减小,α随围压增加而增大。由于不同砂岩内部结构及性质的不同,内部裂隙具有不同的应力敏感性。分选性较差的砂岩应力敏感性强,裂隙维持张开所能承受的应力较低;分选性较好的砂岩应力敏感性较弱,裂隙维持张开所能承受的应力较高。探讨了所定义转折压力与岩石样品物性间的关系,结果表明,两者具有非常好的正相关性。
关键词:围压;含气致密砂岩;裂隙密度;孔隙纵横比;波速;应力敏感性;转折压力
致密砂岩气、页岩气及煤层气作为非常规天然气,是未来国家天然气供应的主要接替能源[1]。但这类含气储层往往具有强非均质性及低孔低渗的特征[2],给天然气勘探开发造成不便。要想实现对该类型油气储层的有效勘探开发,就需要从微尺度方面着手,细致研究其微观储集油气能力及流体运移机理[3]。储层之所以能储集油气,主要因为储层为孔裂隙介质[4],裂隙的存在不仅能为油气赋存提供空间,而且能为油气运移提供通道[5]。裂隙在岩石中的主要存在特征为具有一定裂隙密度及裂隙形态[6](孔隙纵横比),其分布特征在岩石力学、声学及岩石物性方面均有一定响应。前人对不同岩性岩石中的裂隙形态进行了大量试验研究,如裂隙密度ε对干燥及饱水条件下砂岩及灰岩体积模量及剪切模量的影响[7],结果表明岩石模量随ε的增加而降低;李宏兵等[8]研究了不同有效压力条件下花岗岩及砂岩孔隙纵横比α的变化规律,结果表明α随有效压力增加而增加;陈雪莲等[9]研究了裂隙密度ε对低孔低渗含气地层波场的影响,结果表明其影响不容忽视;唐晓明等[10]研究了不同围压条件下Berea砂岩、Troy花岗岩及Westerly花岗岩ε和α的变化规律,结果表明围压对于非常致密的岩石如花岗岩的ε和α的影响非常大。裂隙的大量存在能显著改善储层物性、储集性及导流能力。由于裂隙的存在能引起波场的显著变化[11],因此目前国内外针对孔裂隙介质地层的研究,主要采用室内声学测试及随钻测井相结合的方法[12]。本文采用孔裂隙介质弹性波动原理方法(或称Biot相洽理论方法)[10]及微分等效介质原理[8]对不同围压条件下岩石裂隙密度ε及孔隙纵横比α进行反演,探讨它们的变化规律及影响因素,为地下油气勘探开发提供依据。
1试验样品及测试
对取自深层的4组致密含气砂岩样品(A组为细-中粒(或泥砾)岩屑石英砂岩,B组为细粒长石低孔高密度岩屑砂岩,C组为细粒长石高孔低密度岩屑砂岩,D组为细-中粒长石岩屑砂岩)进行了初始条件下的岩石物理参数测量,测量结果如表1所示。表1中K0和μ0分别为岩石基质矿物体积模量和剪切模量;Kd和μd分别为干岩石骨架体积模量和剪切模量;Ks为饱水及流体压力条件下岩石体积模量。实验设备主要由三轴室、电液伺服控制系统、超声波脉冲发射-接收控制盒、数字存储示波器及计算机等组成。设备全部由计算机自动采集压力、位移和纵横波波速数据,能够保证数据的准确性。压力传感器误差<1%,位移分辨精度为0.0001mm,对于测试的25mm×50mm尺寸样品,超声波换能器频率为1MHz。
砂岩样品取自塔中地区志留系埋深>5000m的浅海陆棚沉积地层,岩性为:细粒岩屑石英砂岩、细粒长石岩屑砂岩及细-中粒长石岩屑砂岩。样品孔隙度分布在5.11%~10.01%,密度分布在2.34~2.45g/cm3(表1),渗透率<1×10-3μm2,属深层低孔-低渗含气致密储层。测试样品尺寸为25mm×50mm圆柱体,表观完整,未见裂缝。对样品进行多级围压加载试验,并同步进行纵、横波波速测试。测试围压共分9级:0,5,10,15,22,32,44,55,66MPa,样品封套饱和地层盐水。4组样品不同围压条件下实测纵、横波波速见表2和图1,随着围压的增加,纵、横波波速均增加。围压较低时波速增幅较大,围压较高时波速增幅较小,岩石纵波波速大于横波波速。

表1 初始条件下岩石物理参数测试结果
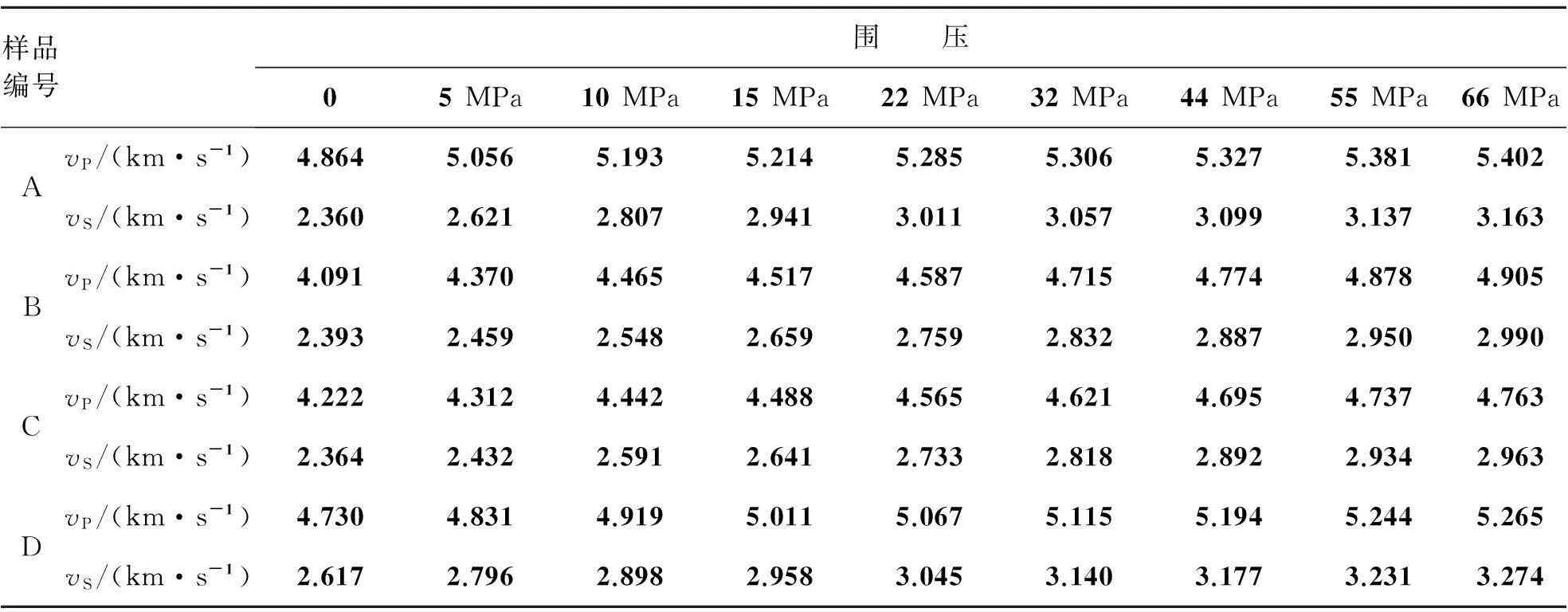
表2 不同加载围压条件下岩石纵、横波波速测试结果

图1 4组致密含气砂岩样品不同加载围压条件下岩石纵、横波波速变化a 细粒岩屑石英砂岩(饱水); b 细粒长石岩屑砂岩(饱水); c 细粒长石岩屑砂岩(饱水); d 细-中粒长石岩屑砂岩(饱水)
2孔隙形态反演方法原理
2.1裂隙密度ε的反演
岩石内部普遍存在孔隙及裂隙,裂隙的存在降低了岩石的体积模量和剪切模量,并在声波测试结果中产生显著响应[11]。因此本文采用Biot相洽理论对岩石裂隙密度ε进行反演。对于孔裂隙介质而言,Biot推导得出的有关岩石体积模量及剪切模量变化的本构方程如下[7]:
(1)
(2)
(3)

(4)
式中:Kf为流体体积模量。
根据公式(2)到公式(4),可以确定pf:
(5)
此时岩石体积模量K可以表示为:
(6)
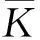
(7)
(7)式中Kf根据Wood方程确定[13];aB,AB及KB求取方法见文献[7];φ和φc取测井解释值,其中,φp=φ-φc。将根据公式(7)求取的岩石体积模量与岩石实测Ks进行对比,当误差最小时即可认为所求取的裂隙密度ε值为最佳值。
反演中4组致密砂岩不同围压条件下实际Ks值与预测值之间的关系见图2。从图2可以看出,随着围压的增加(0~66MPa),4组砂岩Ks值均逐渐增加。A组砂岩在0~10MPa,B,C,D组砂岩在0~5MPa时Ks增加幅度较大。之后A,B,C 3组砂岩Ks增加幅度逐渐变缓,而D组砂岩在围压44MPa之后Ks增幅较大,可能与其内部颗粒排列有关。整体而言,利用方程(7)预测的岩石Ks值与实测值极为相符,因而最终反演得到的裂隙密度ε可靠。
2.2孔隙纵横比α的反演
岩石孔隙纵横比α为岩石椭球状孔隙的短轴与长轴的比值[14],因而α取值范围为0~1。当α>0.1时,孔隙形态主要为球形孔及针形孔;当α<0.1时,孔隙形态主要为币形缝及无限裂缝,因而可以简单以α=0.1作为岩石孔隙和裂隙的分界点[14]。
求取岩石α主要根据BREEYMAN等[15]早期给出的岩石体积模量和剪切模量的耦合常微分方程(微分等效介质理论模型):
(8)
(9)
式中:Ki和μi分别为孔隙内成分的体积模量和剪切模量;K*和μ*分别为考虑基质矿物及孔隙组分的岩石等效体积模量和剪切模量;P*i和Q*i分别为等效体积模量和剪切模量的激化因子。
LI等[16]对方程(8)和方程(9)进行解耦,分别得到干岩石骨架体积模量Kd和剪切模量μd的解析方程:
(10)
(11)
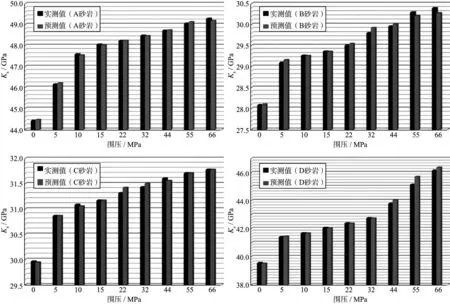
图2 不同围压条件下Ks预测值与实测值对比
其中,S0,S1,S2和S3为α的函数,具体表达式见文献[16];a和b也为α的函数,可由(12)式求出。
(12)
李宏兵等[8]通过对(12)式中的(P*i-Q*i)一阶求导,确定的a值和b值分别为:
a=(P*i-Q*i)-(P*i-Q*i)′K0/μ0
(13)
b=(P*i-Q*i)′
(14)
P*i-Q*i及(P*i-Q*i)′亦为α的函数,具体函数式详见文献[16]。将求取的a和b代入方程(10)或方程(11),通过不断调试α,将反算的Kd或μd与实际结果进行对比。当误差最小时,认为此时反演的α值最可靠。同时李宏兵等[8]指出,利用方程(10)或方程(11)进行α反演时,结果相差不大,因此本文采用方程(10)对α值进行反演。
反演中4组致密砂岩的实际K0,μ0和初始未加压条件下的Kd,μd,Ks及孔隙度和密度值见表1。
3反演结果及讨论
3.1裂隙密度ε反演结果
不同围压条件下4组砂岩裂隙密度ε反演结果见图3。可以看出,随着围压的增加,ε值逐渐降低,这与唐晓明等[10]反演的结果一致。单轴条件下(围压0)ε值较高,各组样品ε值在围压相对较低时降低较快,在围压相对较高时降低速度较缓。4组样品中A组和D组砂岩具有细、中粒度双峰分布形态,镜下可见泥砾,分选性较差。在较高围压条件下ε值降低到了极小值,说明此时几乎所有裂隙均发生了闭合;B组和C组砂岩粒度分选较好,在较高围压条件下仍具有一定ε值分布,表明此时仍具有一些未闭合的裂隙。显然,A组和D组砂岩中的裂隙对应力的敏感程度较高;而B组和C组砂岩中的裂隙对应力的敏感程度较低。在地层较高应力环境下,B组和C组砂岩的裂隙对环境应力具有更强的抵抗能力,能促使裂隙保持张开,对油气赋存及运移均具有重要意义。而A组和D组砂岩中的裂隙在较高应力条件下易发生闭合,对油气赋存运移不利。
3.2岩石孔隙纵横比α反演结果
进一步对不同围压条件下岩石孔隙纵横比α进行分析(图4)。从图4可以看出,随着围压的增加,α值逐渐增加,这主要是由于具有较小α值的部分裂隙的闭合导致的[8]。4组样品在起始加载条件下均以α值<0.01的无限裂缝为主,彼此差别不大。随着围压加载至某一应力值,α值发生跃变,转变为大于0.9的孔隙,表明此时在较高应力条件下岩石中的裂隙几乎全部发生了闭合,岩石内部开放空间以孔隙系统为主。
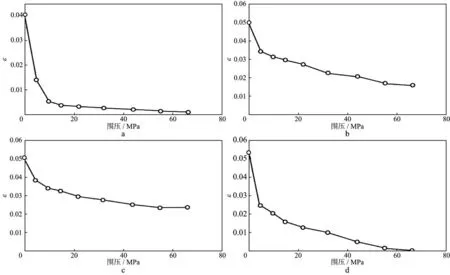
图3 4组致密含气砂岩样品不同围压条件下岩石裂隙密度ε反演结果a 细-中粒(泥砾)岩屑石英砂岩; b 细粒长石岩屑砂岩; c 细粒长石岩屑砂岩; d 细-中粒长石岩屑砂岩

图4 不同围压条件下岩石孔隙纵横比α反演结果
同时可以发现,前述A组和D组砂岩中裂隙的应力敏感性强,随着围压的增加,ε最终趋向于接近0的极小值。这两组砂岩从图5中可以更直观地看出,该裂隙若要维持张开则其所能承受的应力均较低。而对于B组和C组砂岩,其中裂隙维持张开所能承受的应力要明显相对较高。
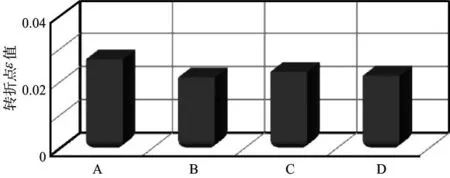
图5 不同砂岩转折点ε值
以图4中岩石α值发生跃变的点,即从裂隙(α<0.1的第1个点)到孔隙(α>0.1的第1个点)间连线的中点作为孔裂隙性质发生急剧变化的转折点。寻找该点对应的裂隙密度ε,4组ε值分别为:0.0273(A),0.0218(B),0.0235(C),0.0223(D)(图5),彼此相差不大,平均值为0.0237,该值可以作为地层条件下该类砂岩中裂隙发育程度的重要指标,高于该ε值时,地层中存在较多张开的裂隙,而低于该ε值时,地层中主要以闭合型的裂隙为主。同时,裂隙研究中,研究对象是微尺度的,因而ε值的微小变化在宏观上可能会产生不可忽视的影响[17]。所定义的ε临界值并不是0,这主要是由于岩石内部其实含有各种尺度孔裂隙,裂隙随应力环境的加大一般不会完全消失。在加载的最后阶段,当绝大部分裂隙闭合时,仍有少量裂隙张开,但整体来说,此时岩石中已经以孔隙系统为主。
我们定义4组砂岩ε值转折点所对应的压力为转折压力,其也是裂隙应力敏感性的重要指标,对应转折压力分别为:2.5MPa(A),38.0MPa(B),60.5MPa(C),7.5MPa(D),该压力值越大代表岩石中裂隙对应力越不敏感,裂隙维持张开所能承受的应力越高。对4组样品转折压力与物性因素(初始孔隙度)的关系进行分析(图6)。从图6可以看出,两者具有非常好的正相关性,B组和C组砂岩中裂隙应力敏感性较弱,其物性也相对较好;A组和D组砂岩中裂隙应力敏感性较强,其物性也相对较差。同时表明本文方法所反演出的岩石孔裂隙空间为有效空间,允许油气分子在其中赋存或运移。
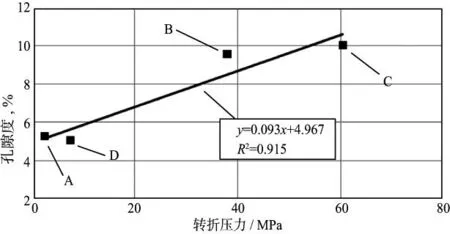
图6 样品转折压力与孔隙度关系
虽然所取岩石样品从宏观尺度观察完整,但反演结果表明其内部还是含有一些微裂隙,这种微裂隙以无限裂缝型为主,也就是说其开度非常小,肉眼无法识别。但其依然占据了不可忽视的裂隙空间,可以使油气分子赋存或运移。这对非常规页岩气储层裂缝评价具有一定参考价值。因为页岩作为横观(横向)各向同性介质[18],纵向非均质性强,其油气存储空间主要为层间页理缝。但由于页岩非常致密,许多层间页理缝很难肉眼识别,而本文方法可以从微观尺度对其进行较有效的评价。
4结论
利用Biot相洽原理及微分等效介质原理对不同围压条件下致密砂岩储层岩石孔裂隙形态演化及分布规律进行研究,避免了单一研究方法的不足。裂隙会随着应力环境的升高而逐渐发生闭合,因而,ε随围压增加而减小,α随围压增加而增大。此外,裂隙的应力敏感性强弱还与岩石的分选性相关。研究表明,孔裂隙性质通常会在某个ε值附近发生急剧变化,该值可以作为地层条件下该类砂岩中裂隙发育程度的重要指标。文中所定义转折压力与岩石样品物性间具有非常好的正相关性,表明裂隙的分布与岩石物性密切相关。该反演方法可以用于定量预测储层微裂缝性质及分布特征。
参考文献
[1]MENG Z P,ZHANG J C,WANG R.In-situ stress,pore pressure and stress-dependent permeability in the Southern Qinshui Basin[J].International Journal of Rock Mechanics&Mining Sciences,2011,48(1):122-131
[2]DVORKIN J,NUR A.Dynamic poroelasticity:a unified model with the squirt and the Biot mechanisms[J].Geophysics,1993,58(4):524-533
[3]BONS P D,ELBURG M A,ENRIQUE G R.A review of the formation of tectonic veins and their microstructures[J].Journal of Structural Geology,2012,43(1):33-62
[4]TANG X M,CHEN X L,XU X K.A cracked porous medium elastic wave theory and its application to interpreting acoustic data from tight formations[J].Geophysics,2012,77(6):245-252
[5]唐晓明.含孔、裂隙介质弹性波动的统一理论-Biot理论的推广[J].中国科学:地球科学,2011,41(6):784-795
TANG X M.A unified theory for elastic wave propagation through porous media containing cracks-an extension of Biot’s poroelastic wave theory[J].Science China:Earth Science,2011,41(6):784-795
[6]陈雪莲,唐晓明.孔、裂隙并存地层中的声波测井理论及多级子声场特征[J].地球物理学报,2012,55(6):2129-2139
CHEN X L,TANG X M.Numerrical study on the characteristics of acoustic logging response in the fluid-filled borehole embedded in crack-porous medium[J].Chinese Journal of Geophysics,2012,55(6):2129-2139
[7]印兴耀,刘欣欣,曹丹平.基于Biot相洽理论的致密砂岩弹性参数计算方法[J].石油物探,2013,52(5):445-451
YIN X Y,LIU X X,CAO D P.Elastic parameters calculation for tight sand reservoir based on Biot-consistent theory[J].Geophysical Prospecting for Petroleum,2013,52(5):445-451
[8]李宏兵,张佳佳,姚逢昌.岩石的等效孔隙纵横比反演及其应用[J].地球物理学报,2013,56(2):608-614
LI H B,ZHANG J J,YAO F C.Inversion of effective pore aspect ratios for porous rocks and its applications[J].Chinese Journal of Geophysics,2013,56(2):608-614
[9]陈雪莲,钱玉萍,唐晓明.裂隙发育对低孔低渗含气地层声传播特征的影响[J].中国石油大学学报(自然科学版),2013,37(4):88-93
CHEN X L,QIAN Y P,TANG X M.Influence of crack on acoustic propagation characteristics in low porosity and low permeability gas reservoir[J].Journal of China University of Petroleum(Edition of Natural Sciences),2013,37(4):88-93
[10]唐晓明,钱玉萍,陈雪莲.孔隙、裂隙介质弹性波理论的实验研究[J].地球物理学报,2013,56(12):4226-4232
TANG X M,QIAN Y P,CHEN X L.Laboratory study of elastic wave theory for a cracked orous medium using ultrasonic velocity data of rock samples[J].Chinese Journal of Geophysics,2013,56(12):4226-4232
[11]HUDSON J A.A higher order approximation to the wave propagation constants for a cracked solid[J].Geophysical Journal Royal Astronomical Society,1986,87(1):265-274
[12]许松,苏远大,陈雪莲,等.含孔隙、裂隙地层随钻多极子声波测井理论[J].地球物理学报,2014,57(6):1999-2010
XU S,SU Y D,CHEN X L,et al.Numerical study on the characteristics of multipole acoustic logging while drilling in cracked porous medium[J].Chinese Journal of Geophysics,2014,57(6):1999-2010
[13]李维新,史哥,王红,等.岩石物理弹性参数规律研究[J].地球物理学进展,2007,22(5):1380-1385
LI W X,SHI G,WANG H,et al.The study on the relationships of elastic properties of rock physics[J].Progress in Geophysics,2007,22(5):1380-1385
[14]董宁,藿志周,孙赞东,等.泥页岩岩石物理建模研究[J].地球物理学报,2014,57(6):1990-1997
DONG N,HUO Z Z,SUN Z D,et al.An investigation of a new rock physics model for shale[J].Chinese Journal of Geophysics,2014,57(6):1990-1997
[15]BREEYMAN J G,BERGE P A.Critique of two explicit schemes for estimating elastic properties of multiphase composites[J].Mechanics of Materials,1996,22(2):149-164
[16]LI H B,ZHANG J J.Elastic moduli of dry rocks containing spheroidal pores based on differential effective medium theory[J].Journal of Applied Geophysics,2011,75(4):671-678
[17]MAVKO G,NUR A.Wave attenuation in partially saturated rocks[J].Geophysics,1979,44(2):161-178
[18]SONDERGELD C H,NEWSHAM K E,COMISKY J T.Petrophysical considerations in evaluating and producing shale gas[J].Expanded Abstracts of 82ndSPE Annual Conference,2007,SPE131768
(编辑:陈杰)
Experimental study on pore/fissure morphology evolution of gas-bearing tight sandstone under different confining pressure conditions
YIN Shuai1,2,3,DING Wenlong1,2,3,SUN Yuanhui4,SHAN Yuming5,WANG Ruyue1,2,3
(1.SchoolofEnergyResources,ChinaUniversityofGeosciences,Beijing100083,China;2.KeyLaboratoryforMarineReservoirEvolutionandHydrocarbonAbundanceMechanism,MinistryofEducation,ChinaUniversityofGeosciences,Beijing100083,China;3.KeyLaboratoryforShaleGasExploitationandAssessment,MinistryofLandandResources,ChinaUniversityofGeosciences,Beijing100083,China;4.ResearchInstituteofPetroleumExploration&Development,CNPC,Beijing100083,China;5.CollegeofEnergyResource,ChengduUniversityofTechnology,Chengdu610059,China)
Abstract:we carry out acoustic test on four groups of deep tight sandstone samples under different confining pressures,inverse the rock fracture density (ε) and pore aspect ratio (α) using Biot-consistent principle and differential effective media theory.By combining the two methods,we can identify the rock pore/fissure morphology evolution and distribution under different confining pressure conditions.It can overcome the deficiency using a single method.The results show that the fracture density decreases while the pore aspect ratio increases along with the increasing confining pressure,which is mainly due to the closure of fractures in high stress environment.Because the internal structure and properties of sandstone is different,there’s different stress sensitivity for internal fractures.The stress sensitivity of poor sorting sandstone of A group and D group is strong,the stress that fracture maintains open is low;the stress sensitivity of good sorting sandstone of B group and C group is weak,the stress that fracture maintains open is high.Discussion on the relationship of defined twist pressure and rock physical properties show a very good positive correlation between them.
Keywords:confining pressure,gas-bearing tight sandstone,fracture density,pore aspect ratio,wave velocity,stress sensitivity,twist pressure
收稿日期:2014-10-22;改回日期:2015-10-10。
作者简介:尹帅(1989—),男,博士,主要从事石油构造分析与控油作用、页岩气构造和裂缝及其与含气量关系等方面的研究。 通讯作者:丁文龙(1965—),男,教授,长期从事石油构造分析与控油作用、页岩气构造和裂缝及其与含气量关系等方面的教学与科研工作。
基金项目:国家自然科学基金面上项目(41372139,41072098)和国家科技重大专项(2016ZX05046-003-001,2011ZX05018-001-002,2011ZX05033-004)联合资助。
中图分类号:P631
文献标识码:A
文章编号:1000-1441(2016)03-0326-07
DOI:10.3969/j.issn.1000-1441.2016.03.002
This research is financially supported by the National Natural Science Foundation of China(Grant No.41372139 and 41072098)and National Science and Technology Major Project of China (Grant Nos.2016ZX05046-003-001,2011ZX05018-001-002 and 2011ZX05033-004).
