时频面的双曲网格剖分及其应用

董建华

(中海油研究总院,北京100028)

时频面的双曲网格剖分及其应用

董建华

(中海油研究总院,北京100028)

摘要:地层介质对地震波的吸收衰减是传播时间与频率乘积C的函数。在与吸收衰减相关的处理过程中(如品质因子估计、Gabor反褶积等),经常涉及时频面的双曲网格剖分,不同的剖分方式对处理效果有不同的影响。基于此给出了4类网格离散采样方式,分别具有等步长(等间隔网格)和变步长特征(等长度、等衰减和等面积网格),并对4类网格离散采样的采样特点进行了对比分析。在网格数固定的情况下,具有变步长特征的网格在低C值区加密采样、在高C值区稀疏采样。模型数据测试和实际资料应用表明,衰减记录时频谱振幅的衰减曲线在低C值区间具有较好的稳定性,如果利用变步长网格对时频谱进行统计,可以得到更多合理可靠的采样数据点,更利于振幅曲线的线性拟合。

关键词：吸收衰减;时频谱;双曲网格;变步长;线性拟合

地震波在地下介质中传播时,受到地下介质的吸收衰减作用等因素的影响,使得地震信号呈非稳态特征,严重影响了中深层的成像能力以及储层预测的精度[1-2]。吸收补偿是解决地层介质吸收效应的有效手段,主要有反Q滤波[3]、反Q偏移[4-5]等。其中,直接影响吸收补偿效果的因素是地层Q值,因此地层Q值的估算尤为重要。常用Q值估算方法的基本思路是将地震波振幅表示成时间和频率的函数,再根据该函数对测量数据进行一维或二维拟合[6-9]。Gabor反褶积是另一类改善地震记录非稳态特征的技术[10],基于非稳态地震道褶积模型的假设[11-14],反射系数、初始地震子波和吸收衰减因子在Gabor时频域可以较好地分离。在此基础上,陆续有学者对该方法进行了推广和应用。李芳等[15]将叠前道集从XT域转换到径向道RT域,使其更符合非稳态反褶积的假设;陈增保等[16]、SUN等[17-18]、赵岩等[19]利用非稳态反褶积技术消除地震记录的非稳态特征(即吸收衰减项),再结合常规反褶积技术(如稀疏约束反褶积等)实现地震资料的拓频处理,取得了较好的应用效果;王本锋等[20]基于非稳态褶积模型,利用反演策略估算吸收衰减函数,规避常规Gabor反褶积的子波最小相位假设,实现非稳态数据的自适应衰减补偿处理。

根据KJARTANSSON衰减模型[21],地层介质的吸收衰减项是传播时间与频率乘积的函数,在时间-频率平面上表现为双曲特征。在与吸收衰减有关的处理过程中,无论是Q值估算还是Gabor反褶积等,都有可能涉及到时频面双曲网格剖分这一关键点。常规的剖分方式是将时间与频率的乘积视作自变量,并进行等间隔采样。但是等间隔采样不符合地震记录的实际情况,容易造成以有效信号为主的强能量区域欠采样,而以噪声为主的低能量区域过采样[15,20]。基于此,我们提出了变步长双曲采样方法(对变量指数衰减值进行等间隔采样),对弱衰减(以有效信号为主)的区域进行加密采样,对强衰减(以噪声为主)的区域进行稀疏采样,以提高反褶积因子的估算精度。

事实上,时频双曲网格不同于常规的矩形网格,其剖分方式并不局限于上述两种思路,还可以是等长度或等面积采样。由于时间和频率方向上的采样都是均匀的,时频面上单位面积包含的采样点数恒定,如果采用等面积双曲网格采样方式,可以保证每个网格包含的采样点数基本相同,均匀采样将有利于统计特征的分析。我们系统给出不同的双曲网格采样方法,并对采样特点进行分析对比,为后续的能量统计提供合理可行的剖分方式。模型测试和实际资料应用表明,具有变步长特征的网格能在有效区间获得比等步长网格更多的采样数据,更利于衰减系数(如Q值)的合理估计。

1方法原理

根据吸收衰减模型,地震波频谱的振幅A(f,t)按如下方式衰减:

(1)

式中:Q为品质因子;v为速度;L为传播距离。

当假设地层为常速均匀介质时,则有:

(2)

式中:t为传播时间。

根据(2)式,地震波的振幅随传播时间和频率2个参量变化,为方便处理,一般将时间和频率的乘积f·t看作一个参量(设为C),从而将一维(时间或频率方向)衰减转换为二维(时频平面)衰减。当估算Q值时,可以拟合曲线ln[A(f,t)/A(f,0)]—C的斜率k,并转换为Q值(Q=-π/k)。由于相同的C值具有相同的衰减量,因此,需要沿着时频平面的双曲线进行数据样本统计,其中涉及到双曲网格的剖分问题。

双曲网格的剖分问题可归纳为:假设时间变量为t,取值区间为[0,T],频率变量为f,取值区间为[0,f],则t和f组成一个时频平面,在该矩形框内按照双曲线进行网格剖分,双曲线满足方程:

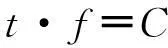
(3)

其中,C为待定值,取值区间为[0,TF],只要确定了离散采样点Ck,k=1,2,…,N,即可确定整个双曲网格。

已有的双曲网格有等间隔和等衰减网格,在此基础上,给出两种新的双曲网格定义,即等长度和等面积网格,并推导出4种网格的具体采样方式。

1.1等间隔网格

等间隔网格即参照矩形网格的剖分方式,将C的取值区间进行N等分并进行离散采样:

(4)

等间隔网格的特点是Ck值等间隔划分。

1.2等长度网格

双曲线在几何上关于对角线对称,等长度网格的思路是将时频矩形框在对角线上的长度进行N等分,对角线满足方程:

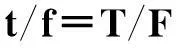
(5)

离散采样方式:

(6)

等长度双曲网格的特点是确保在对角线附近的采样均匀。

1.3等衰减网格

(7)

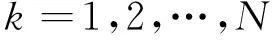
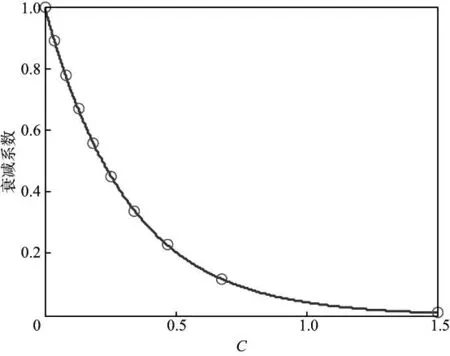
图1　衰减系数—C曲线

事实上,等衰减网格就是文献[15]中的变步长采样双曲网格(由于本文中的多个网格都具有变步长特征,因此这里记为等衰减网格)。等衰减网格的特点是每隔一定的衰减量进行一次数据样本统计,可以有效加密低C值区域(衰减量|α|变化较快)采样。

1.4等面积网格

在时频面上,单位面积覆盖的样点数是均匀的;在样本统计中,一般期望单个双曲网格中的样本数相同。等面积网格是将时频矩形框的面积进行N等分。

首先,计算双曲线t·f=C,直线t=0,f=0,t=T和f=F五条线围成的图形(图2中的阴影区域)面积S:

(8)

公式(8)表明,双曲线围成的面积S与时间与频率乘积值C呈非线性关系。图3中蓝线是面积S与C值的曲线,可以看到,C越大,S越大,但增速越缓。

其次,对(8)式微分,并令ΔS≈dS,ΔCk≈dC(当ΔCk较小时),则有:

(9)

根据公式(8),有离散采样方式:

(10)

图3中红圈代表的面积值具有相同的增量ΔS,随着C的增加,增量ΔC逐渐增大,这与等衰减网格类似,说明两者都具有变步长特征。等面积网格的特点是确保网格内样本统计的个数一致。

从步长的角度出发,上述4种网格剖分方式还可以归纳为等步长(等间隔网格)和变步长(等长度、等衰减和等面积网格)两大类。

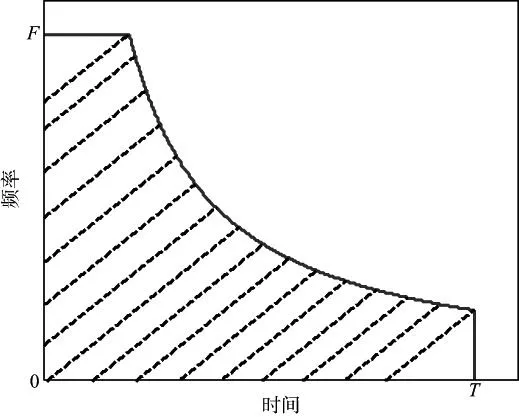
图2　时间—频率面积示意

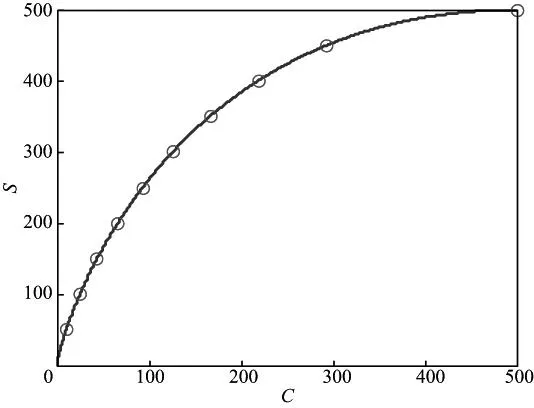
图3　S—C曲线

2网格剖分

模型设定时间长度为2s,2ms采样,截止频率为250Hz,0.5Hz采样,时频网格的总样本数约为5×105个。利用上述4类离散采样方式对时频框进行双曲网格剖分,网格数为N。

图4是N取10的双曲网格剖分图,其中,图4a为等间隔网格,图4b为等长度网格,图4c为等衰减网格,图4d为等面积网格。从图4中可以看到,等间隔网格对时频框的剖分严重不均匀,低C值区(左上部分,下同)的网格明显大于高C值区(右下部分,下同)的网格;等长度网格在对角线(蓝线)方向上等间距,即在对角线附近的采样均匀;等衰减网格在低C值区较为密集,在高C值区则相对稀疏;等面积网格与等衰减网格类似,不同的是,等衰减网格在高C值区比等面积网格更稀疏。

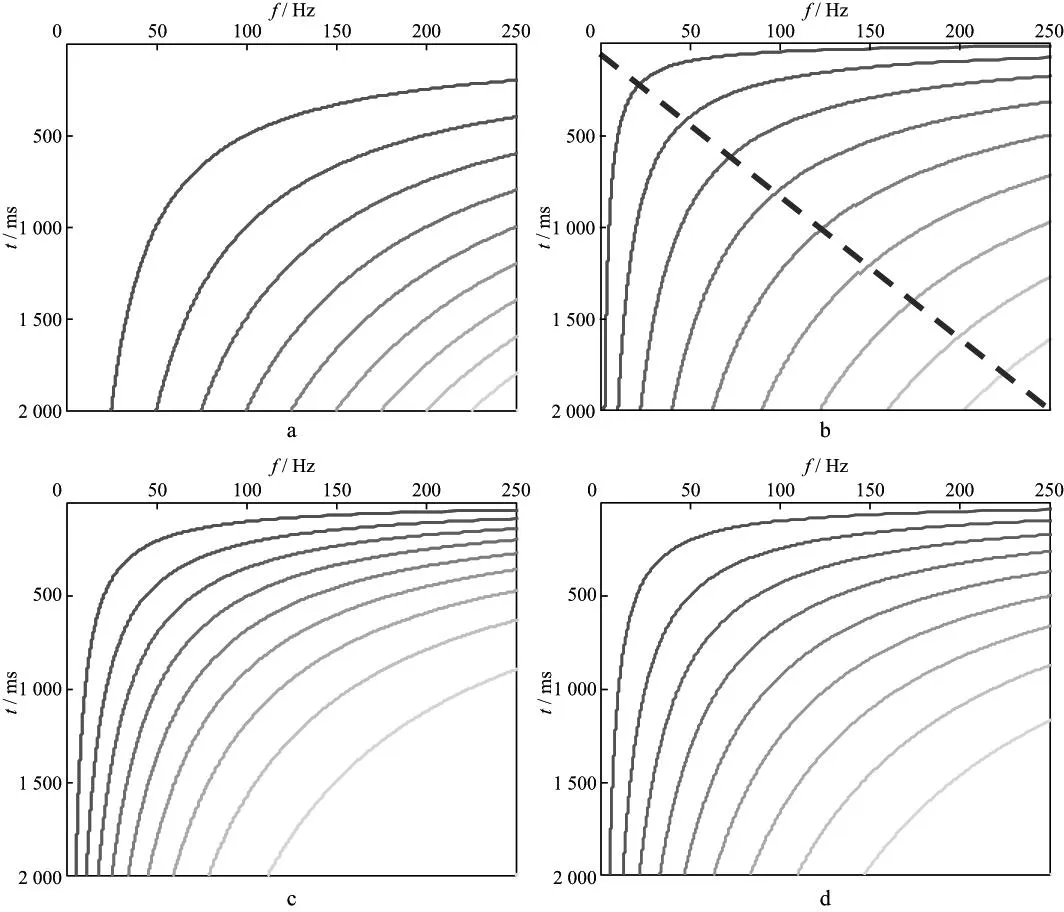
图4　双曲网格剖分(N=10)a 等间隔网格; b 等长度网格; c 等衰减网格; d 等面积网格

图5是不同双曲网格步长ΔC与C值曲线,其中,蓝色标记为等间隔网格步长,红色标记为等长度网格步长,粉色标记为等衰减网格步长,黑色标记为等面积网格步长。可以看到,等间隔网格的步长与C值无关,保持不变;余下3个网格均具有变步长特征,步长随着C值的增加而变大,同时,在低C值区加密采样,在高C值区稀疏采样,其中,等衰减网格在低C值区的采样最密集、在高C值区的采样最稀疏,等面积网格次之。

图6是4类双曲网格在单个网格内的统计样本数,其中,图6a为等间隔网格,图6b为等长度网格,图6c为等衰减网格,图6d为等面积网格。由图6可以看到,等间隔网格的样本数随着C值的增加而快速下降,第一个网格和最后一个网格的统计样本数相差102量级;等长度网格的样本数呈先增后减的趋势,在C值为50附近的区间,样本数较为均衡,最大样本数与最小样本数相差101量级;等衰减网格的样本数呈先减后增的趋势,与等长度网格类似,在C值为50附近的区间,样本数较为均衡,最大样本数与最小样本数在同一个量级;等面积网格的样本数与C值无关,只存在轻微的波动(主要由网格端点统计偏差及面积等分误差等引起),波动幅度在5%以内。

图7,图8和图9是N=20时网格剖分情况,其趋势特征分别与图4,图5和图6类似,这里只展示图例,不作赘述。

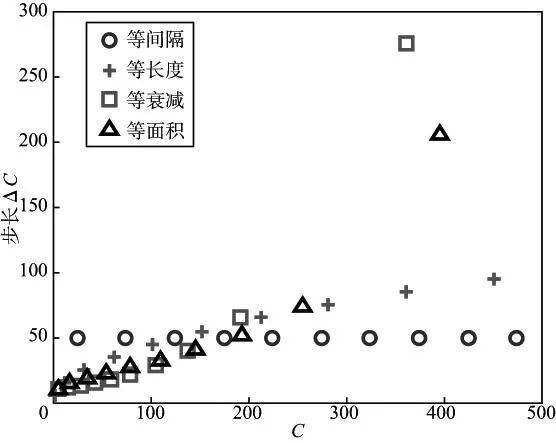
图5　步长ΔC与C值曲线(N=10)

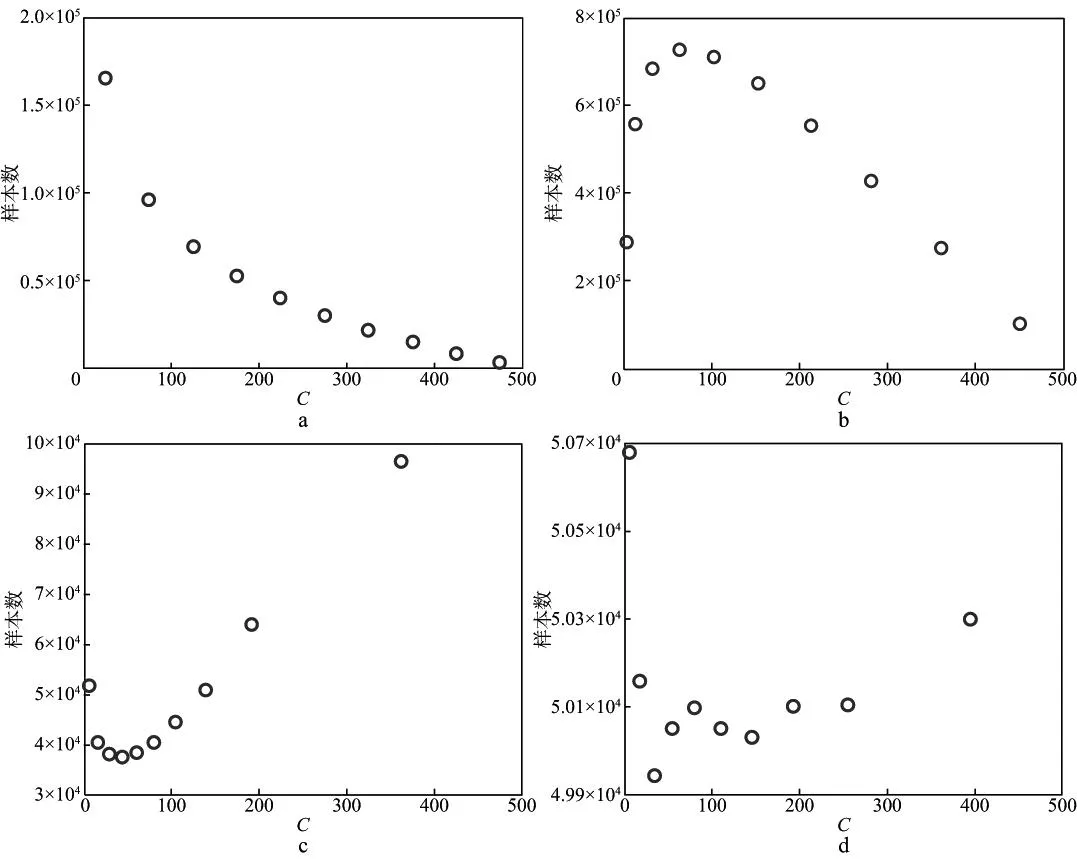
图6　双曲网格样本数(N=10)a 等间隔网格; b 等长度网格; c 等衰减网格; d 等面积网格

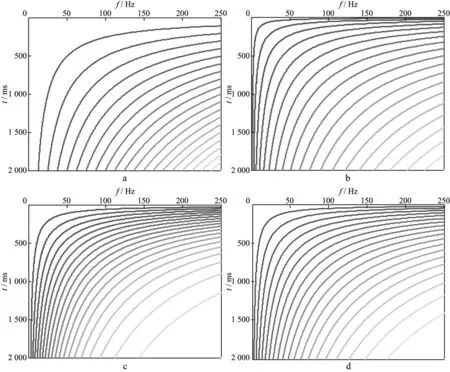
图7　双曲网格剖分(N=20)a 等间隔网格; b 等长度网格; c 等衰减网格; d 等面积网格

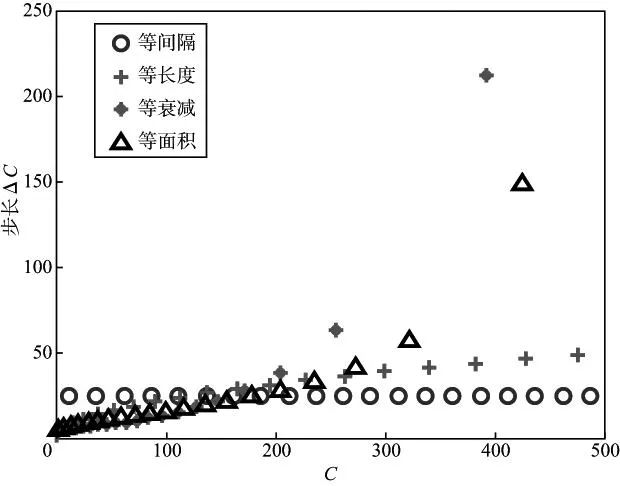
图8　步长ΔC与C值曲线(N=20)

综上所述,等间隔网格对时频面的划分不均匀,低C值区稀疏、高C值区密集,不同网格内的样本数差异可达102量级;等长度网格在时频框对角线方向上较为均匀,不同网格内的样本数差异约为101量级;等衰减网格的划分相对均匀,不同网格内的样本数在同一量级,低C值区较为密集,但高C值区过于稀疏,导致该区网格内样本数多于低C值区的网格;等面积网格的划分较为均匀,不同网格内的样本数基本一致,对高C值区的网格划分相对加密,步长介于等长度网格和等衰减网格之间。

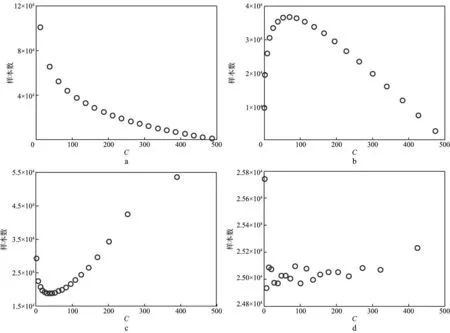
图9　双曲网格样本数(N=20)a 等间隔网格; b 等长度网格; c 等衰减网格; d 等面积网格

3模型测试

首先,基于非稳态褶积模型合成地震记录,初始地震子波取50Hz主频Ricker子波,反射系数为随机序列,地下介质为常Q介质(Q=100),传播时长为2s,时间采样间隔为2ms。其次,利用4类双曲网格分别对合成记录的时频谱进行统计(网格数N取20),得到振幅对数与C值的曲线。

图10a是无噪合成记录(左)及其时频谱(右),合成记录的能量随着传播时间的增加逐渐减小;时频谱的主频和带宽随着传播时间的增加呈下降趋势。图10b是4类网格统计得到的振幅的对数(lgA)与C值曲线,蓝线为理论值,红圈为统计得到的测量值(下同),其斜率k反映了品质因子大小(kQ=-π)。从图10b上可以看到,在C值区间为[0,150]时,测量值与理论值的走向基本一致,区别是在该区间上不同网格的采样点数不同,等间隔网格为6个,等长度网格为10个,等衰减网格为16个,等面积网格为13个。利用测量值的斜率反演Q值,结果分别为等间隔Q值92.92,等长度Q值101.76,等衰减Q值97.14以及等面积Q值98.66,其中,等间隔网格的结果与模型值(100)的误差最大,说明其在[0,150]区间上的采样过于稀疏,缺乏足够的采样信息进行有效的拟合。

图11a是含噪合成记录(信噪比SNR=20)(左)及其时频谱(右),从时频谱上可以看到,在[100,150]的高频段出现了随机干扰。图11b是4类网格统计得到的振幅对数(lgA)与C值的曲线。由于噪声的存在,测量值在[0,100]区间上的走向与理论值基本接近,在[100,150]区间上的走向明显偏离了理论曲线。利用测量值的斜率反演Q值,拟合区间为[20,100],4种网格下的结果分别为127.59,123.15,118.62和115.25。

图12a是含噪合成记录(信噪比SNR=10)(左)及其时频谱(右),高频段的干扰更明显。图12b 是4类网格统计得到的振幅对数(lgA)与C值的曲线,由于噪声增强,符合理论曲线趋势的测量值主要分布于区间[0,60]。利用测量值的斜率反演Q值,拟合区间为[20,70],4种网格下的结果分别为138.51,130.17,130.29和129.28。

事实上,Q值反演结果同时还受拟合区间等因素的影响,上述结果的对比是为了展示不同网格剖分的特点及其对最终结果可能产生的影响。例如,在图12b中,符合理论趋势的区间为[20,70],等间隔网格在该区间仅有2个采样点,显然缺乏足够的有效数据参与线性拟合。当然,等间隔网格可以通过增加网格数N来达到加密低C值区的效果,但高C值区同时得到加密,而高C值区的加密采样统计无益于线性拟合,这意味着增加了大量无用的统计运算。

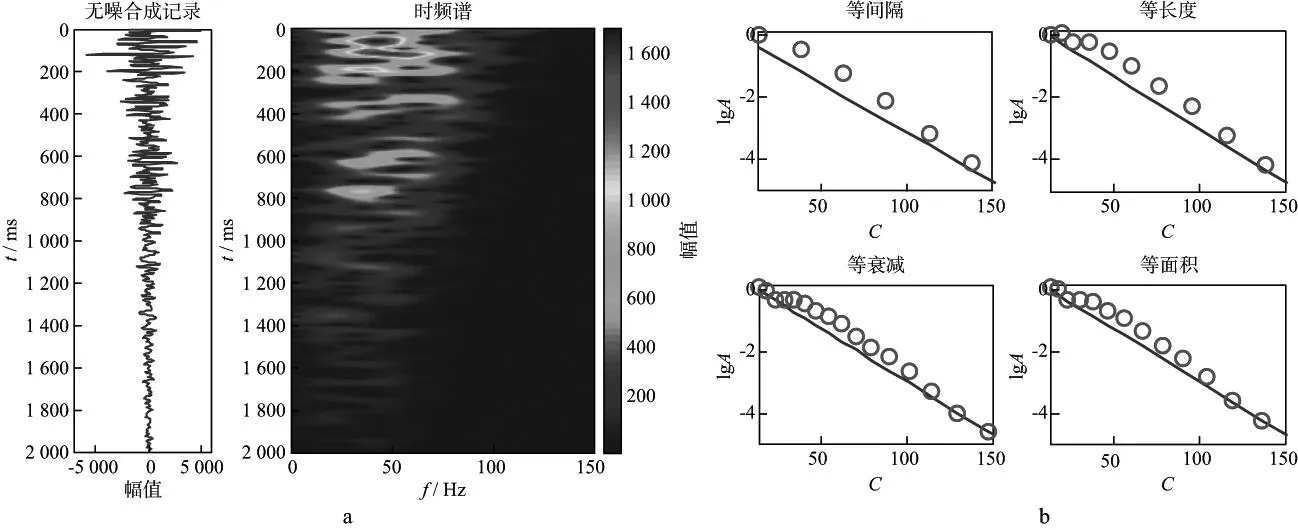
图10　无噪模型测试a 无噪合成记录及其Gabor时频谱; b 4种网格统计的振幅对数(lgA)与C曲线(蓝色:理论值;红色:测量值)

图11　含噪模型测试(SNR=20)a 含噪合成记录及其Gabor时频谱; b 4种网格统计的振幅对数(lgA)与C曲线(蓝色:理论值;红色:测量值)

一般情况下,时频谱中低C值区的抗噪性和准确性优于高C值区,在相同网格数N的情况下,对低C值区进行加密采样可以获得尽可能多的符合衰减趋势的数据点,这对于线性拟合有利。因此,等衰减网格和等面积网格符合这种条件,是较为合理的网格剖分方式;等长度网格尽管对低C值区进行了加密采样,但达不到等衰减和等面积的加密程度;等间隔网格则较难满足这种要求。

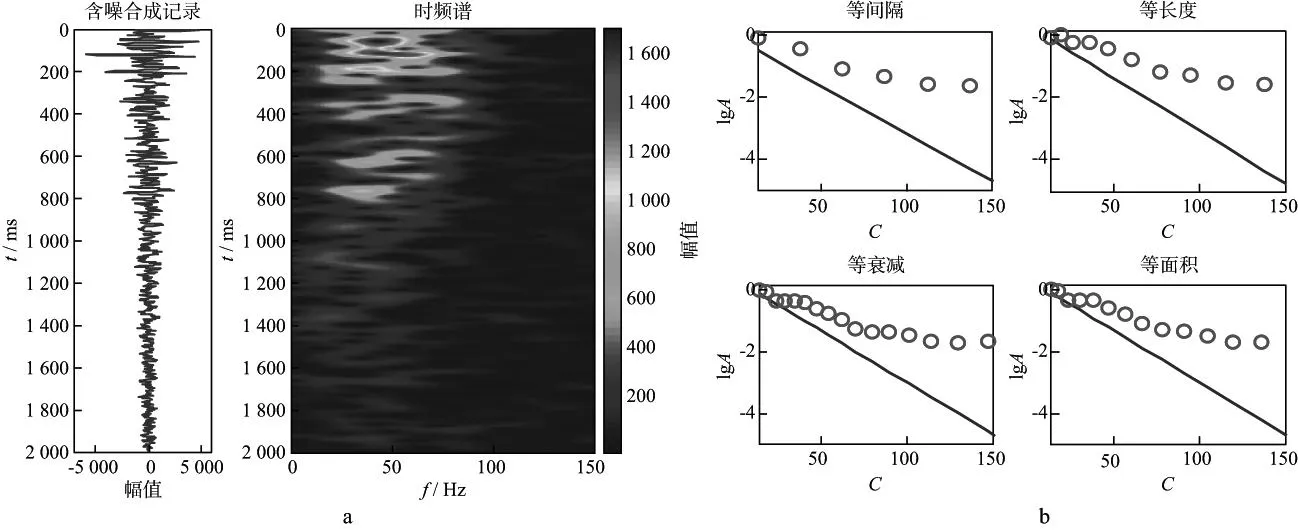
图12　含噪模型测试(SNR=10)a 含噪合成记录及其Gabor时频谱; b 4种网格统计的振幅对数(lgA)与C曲线(蓝色:理论值;红色:测量值)

4实际算例

实际地震资料是来自海上的VSP下行波记录,1ms采样,检波间距为10m。图13a是下行波剖面,提取其初至波谱,并将各道的初至谱合成到同一时频谱上(图13b)。从时频谱上可以看到,地震波的振幅分布近似呈双曲衰减规律。根据资料的实际情况,对该时频谱的处理方式是每传播50ms提取一个Q值、频带范围取[0,100Hz],需要对时间跨度为50ms,频率跨度为100Hz的时频面进行网格剖分。图14是4个网格剖分示意图(网格数为20),图14a为等间隔网格,图14b为等长度网格,图14c为等衰减网格,图14d为等面积网格。图15是根据4个网格采样统计的振幅对数(lgA)—C值曲线,其中,蓝线为等间隔网格提取,红线为等长度网格提取,紫线为等衰减网格提取,黑线为等面积网格提取,4条曲线的趋势基本一致,但采样步长和局部细节存在一定的差异。图16 是估算的地层Q值曲线,其中,青线为根据Q-V经验公式估算的参考Q值(经验值),可以看到,4个网格提取的Q值曲线趋势基本一致,走向符合参考Q值的规律;在局部细节上有一定的区别,如250ms附近(红圈部分),等间隔网格提取的曲线有明显的上突,等衰减网格提取的曲线有明显的下陷,等面积网格提取的曲线相对平稳,而参考曲线在该段并无明显的变化。根据图15的曲线,当C值分布在[0.7,2.7]时,曲线符合理论假设;考察4个网格的采样情况,等面积网格在该有效区间上(图14中的浅绿色阴影区域)的采样比其余3个网格密集,能用于有效拟合的采样点更多。从这个角度考虑,更倾向于等面积网格提取的Q值曲线。

(11)

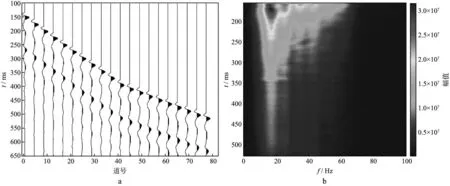
图13　零偏VSP记录及其初至波频谱a VSP下行波记录; b 初至波频谱

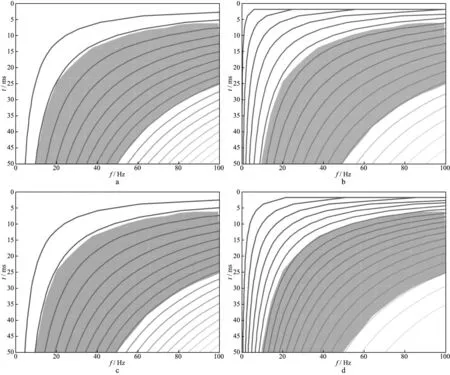
图14　双曲网格剖分(N=20)a 等间隔网格; b 等长度网格; c 等衰减网格; d 等面积网格

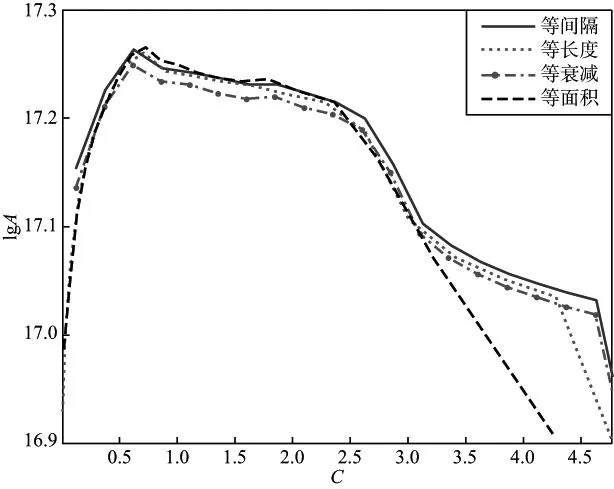
图15　振幅对数(lgA)与C曲线

图16　Q值曲线

5结束语

在已有的两类时频面双曲网格剖分方法基础上,重新定义了两类新的剖分方法,并给出了具体的离散采样方式。通过分析各类网格的特点,取得了如下认识:

1) 等间隔网格是等步长采样,等长度网格、等衰减网格、等面积网格是变步长采样,其中,等衰减网格步长增速可调、等面积网格步长增速较快、等长度网格步长增速较慢。

2) 等间隔网格对低C值区稀疏采样、对高C值区密集采样,等长度网格在时频框对角线附近采样相对均匀,等衰减(以模型参数取100为例)和等面积网格对低C值区密集采样、对高C值区稀疏采样。

3) 单个网格内的统计样本数表明,等间隔网格的样本数分布明显不均,个数相差达102量级,等长度网格的样本数相差达101量级,等衰减网格(以模型参数取100为例)的量级基本一致,等面积网格的样本数基本一致。

4) 理论模型时频谱振幅曲线统计结果显示,符合理论衰减假设的曲线段往往分布在低C值区,在网格数N固定的情况下,等步长采样(等间隔网格)有可能对低C值区间采样不足,变步长采样(等长度、等衰减和等面积网格)则可以在低C值区间采样得到相对更多的可靠数据,更有利于线性拟合。实际资料应用也证实了这点。

5) 在模型测试或实际应用中,可以根据期望的剖分特征来选择合适的剖分方式;在处理与吸收衰减相关的数据时,建议采用变步长网格,需要注意的是,对于不同的时频面,等衰减网格需要通过调节参数才能起到相同的剖分效果。

参考文献

[1]严红勇,刘洋.地震资料Q值估算与反Q滤波研究综述[J].地球物理学进展,2011,26(2):606-615

YAN H Y,LIU Y.A summary of research on estimation ofQand inverseQfiltering for seismic wave[J].Progress in Geophysics,2011,26(2):606-615

[2]李金丽,李振春,管路平,等.地震波衰减及补偿方法[J].物探与化探,2015,39(3):456-465

LI J L,LI Z C,GUAN L P,et al.The method of seismic attenuation and energy compensation[J].Geophysical and Geochemical Exploration,2015,39(3):456-465

[3]郭建,王咸彬,胡中平,等.Q补偿技术在提高地震分辨率中的应用——以准噶尔盆地Y1井区为例[J].石油物探,2007,46(5):509-513

GUO J,WANG X B,HU Z P,et al.Application ofQcompensation technique in improving seismic resolution:case study of Y1 well area,Junggar basin[J].Geophysical Prospecting for Petroleum,2007,46(5):509-513

[4]任浩然,王华忠,张立彬.沿射线路径的波动方程延拓吸收与衰减补偿方法[J].石油物探,2007,46(6):557-561

REN H R,WANG H Z,ZHANG L B.Compensation for absorption and attention using wave equation continuation along ray path[J].Geophysical Prospecting for Petroleum,2007,46(6):557-561

[5]张立彬,王华忠.稳定的反Q偏移方法研究[J].石油物探,2010,49(2):115-120

ZHANG L B,WANG H Z.A stable inverseQmigration method[J].Geophysical Prospecting for Petroleum,2010,49(2):115-120

[6]REINE C,CLARK R,BAAN M.Robust prestackQ-determination using surface seismic data:part 1-method and synthetic examples[J].Geophysics,2012,77(1):R45-R56[7]王小杰,印兴耀,吴国忱.基于S变换的吸收衰减技术在含气储层预测中的应用研究[J].石油物探,2012,51(1):37-41

WANG X J,YIN X Y,WU G C.The application of an S transform based absorption and attenuation technique for prediction of gas-bearing reservoir[J].Geophysical Prospecting for Petroleum,2012,51(1):37-41

[8]魏文,王小杰,李红梅.基于叠前道集小波域Q值求取方法研究[J].石油物探,2011,50(4):355-360

WEI W,WANG X J,LI H M.Study on extraction method forQbased on pre-stack gather in wavelet domain[J].Geophysical Prospecting for Petroleum,2011,50(4):355-360

[9]陈文爽,管路平,李振春,等.基于广义S变换的叠前Q值反演方法研究[J].石油物探,2014,53(6):706-712

CHEN W S,GUAN L P,LI Z C,et al.PrestackQ-inversion based on generalized S transform[J].Geophysical Prospecting for Petroleum,2014,53(6):706-712

[10]孙学凯,孙赞东,谢会文,等.非稳态地震稀疏反褶积[J].石油地球物理勘探,2015,50(2):260-266

SUN X K,SUN Z D,XIE H W,et al.A nonstationary perspective on sparse deconvolution[J].Oil Geophysical Prospecting,2015,50(2):260-266

[11]MARGRAVE G F.Theory of nonstationary linear filtering in the Fourier domain with application to time variant filtering[J].Geophysics,1998,63(1):244-259

[12]MARGRAVE G F,GIBSON P C.Grossman J P,et al.Gabor deconvolution:theory and practice[J].Expanded Abstracts of 66thEAGE Annual Conference,2004:99-102

[13]MA Y W,MARGRAVE G F.Seismic depth imaging with the Gabor transform[J].Geophysics,2008,73(3):S91-S97

[14]MARGRAVE G F,LAMOUREUX M P,HENLEY D C.Gabor deconvolution:estimating reflectivity by nonstationary deconvolution of seismic data[J].Geophysics,2011,76(3):W15-W30

[15]LI F,WANG S D,CHEN X H,et al.Pre-stack nonstationary deconvolution based on variable-step sampling in the radial trace domain[J].Applied Geophysics,2013,10(4):423-432

[16]陈增保,陈小宏,李景叶,等.一种带限稳定的反Q滤波算法[J].石油地球物理勘探,2014,49(1):68-75

CHEN Z B,CHEN X H,LI J Y,et al.A band-limited and robust inverseQfiltering algorithm[J].Oil Geophysical Prospecting,2014,49(1):68-75

[17]SUN X K,SUN Z D,ZHOU X Y,et al.Gabor deconvolution based on hyperbolic smoothing in log spectra[J].Expanded Abstracts of 75thEAGE Annual Conference,2013:478-482

[18]SUN X K,SUN Z D,XIE H W.Nonstationary sparsity-constrained seismic deconvolution[J].Applied Geophysics,2014,11(4):459-467

[19]赵岩,刘洋,胡光义,等.基于衰减补偿的地震资料高分辨率处理方法[J].石油物探,2014,53(1):38-45

ZHAO Y,LIU Y,HU G Y,et al.High resolution processing method of seismic data based on attenuation compensation[J].Geophysical Prospecting for Petroleum,2014,53(1):38-45

[20]王本锋,陈小宏,李景叶,等.基于反演策略的数据自适应衰减补偿方法[J].石油物探,2014,53(3):304-312

WANG B F,CHEN X H,LI J Y,et al.Inversion based data-adaptive attenuation compensation method[J].Geophysical Prospecting for Petroleum,2014,53(3):304-312

[21]KJARTANSSON E.ConstantQ-wave propagation and attenuation[J].Journal of Geophysical Research,1979,84(B9):4737-4748

(编辑：朱文杰)

Hyperbolic bins subdivision in the time-frequency plane and its application

DONG Jianhua

(CNOOCResearchInstitute,Beijing100028,China)

Abstract:Absorption attenuation is a function of a variable C,the product of proporgation time and frequency.The distribution of hyperbolic bins in time-frequency plane is often referred in processing about absorption attenuation (e.g.estimation of quality factor and Gabor deconvolution).Different distributions have different effects on processing.Based on different assumptions,4 types of discrete sampling are defined,which are characteristic of fixed-step sampling (fixed-interval hyperbolic bins) and variable-step sampling (fixed-length,fixed-attenuation and fixed-area hyperbolic bins).When the number of bins is set,variable-step sampling can densely sample in the region with low value C and sparsely sample in the region with high value C.Modeling test and actual data application shows that the amplitude attenuation curve is more stable in the region with low value C than that of in high value C.In that case,if amplitude curve is estimated by variable-step sampling in time-frequency spectrum,more reasonable and reliable specimens can be achieved,which is beneficial for linear fitting of amplitude curve.

Keywords:absorption attenuation,time-frequency spectrum,hyperbolic bin,variable-step,linear fitting

收稿日期：2015-11-06;改回日期：2016-02-05。

作者简介：董建华(1982—),男,硕士,主要从事地震资料处理方法研究工作。

基金项目：国家科技重大专项“海上开发地震关键技术及应用研究”(2011ZX05024-001)资助。

中图分类号：P631

文献标识码：A

文章编号：1000-1441(2016)03-0365-11

DOI:10.3969/j.issn.1000-1441.2016.03.007

This research is financially supported by the National Science and Technology Major Project of China (Grant No.2011ZX05024-001).