遥感影像亚像素快速配准方法

周靖鸿，朱建军，周　璀，樊东昊

(中南大学 地球科学与信息物理学院，湖南 长沙 410083)



遥感影像亚像素快速配准方法

周靖鸿，朱建军，周璀，樊东昊

(中南大学 地球科学与信息物理学院，湖南 长沙 410083)

摘要：针对经典亚像素配准算法运算效率不高的情况，提出一种快速亚像素配准方法。在原有傅里叶变换相位相关方法与矩阵乘法离散傅里叶变换方法的基础上，利用有效子图代替原图进行图像亚像素配准。有效子图是通过二维小波分解高频分量的能量总和大小来选取，再对有效子图进行相位相关像素级定位与矩阵乘法傅里叶变换亚像素定位。改进方法不但继承矩阵乘法离散傅里叶变换亚像素高精度配准的优良性能，而且选用有效子图替代原图进行配准其速度可大大提高，对海量数据的遥感影像更显优势。经模拟试验与工程实例，综合分析该方法的配准精度与配准速度，证明改进方法较经典亚像素配准算法效率更高，更适合用于实际遥感影像的高精度配准。

关键词：亚像素配准；有效子图；相位相关；归一化互功率谱；矩阵乘法离散傅里叶变换；Fourier-Mellin变换

随着遥感技术的飞速发展，获取遥感数据的技术逐渐趋向多平台、多传感器、多角度和高时间分辨率、高空间分辨率、高光谱分辨率的三多三高时代[1]。因此，获得航空航天遥感数据的信息量成倍增大[2]。近年来利用一幅或多幅同一场景的低分辨率遥感影像经超分辨率重建生成一幅高分辨率遥感影像已成为研究的热点，而影像重建过程中低分辨率影像间的亚像素配准精度与效率显得尤为重要[3]。

图像像素级配准的方法很多[4-5]，目前图像亚像素配准算法：插值法[6-7]、扩展相位相关[8]和解最优化问题[9-11]。插值法的性能受内插算法的影响；解最优化问题求解精度虽高，但在实际应用中计算量非常大[12]。而相位相关法能将两者的性能相互综合，其范围包括了空域的相位相关[7,12]和频率域的相位相关。频率域相位相关方法最早由Kuglin[13]在求解图像平移参数时提出，配准精度可达到像素级；在此基础上高莹莹[14]、Lee[15]、De[16]、Chen[17]、Reddy[18]等人利用了Fourier-Mellin变换将图像配准扩展到了具有旋转、平移、缩放等不同情况，但涉及到的都只是像素级的配准；后来Soummer[19]等人提出了矩阵乘法傅里叶变换用于图像的亚像素配准，该方法是以相位相关像素级配准为基础，在求得整数位移的一定邻域范围内进行上采样离散傅里叶变换，其配准精度相对于传统的亚像素配准方法效果要好[20]。该方法数据量较大时计算量也较大，对于海量的遥感数据不太实用。图像的平移是一个整体过程，局部平移信息能反映整幅图像的平移变化。针对遥感影像提出一种改进的亚像素配准方法，利用小波变换选取局部有效子图代替原图，采用矩阵乘法傅里叶变换求取亚像素级位移，通过有效子图的替代减少计算量从而提高配准效率。方法融入Fourier-Mellin变换[18]，当影像间存在旋转、缩放、平移变换时同样适用。该方法进行亚像素配准可大大缩短配准过程的计算量提高配准效率，与传统的方法[21]相比该方法在满足亚像素配准精度要求的同时能成倍提高配准效率，适用于遥感影像海量数据的配准。

1亚像素配准的关键技术

1.1归一化相位相关法

从Kuglin[13]提出相位相关算法用于求取图像的平移参数开始，图像傅里叶变换频率域配准方法被人们广泛应用。设参考图像为f(x,y)，配准图像为g(x-x0,y-y0)，两图像之间位移为(x0,y0)，相位相关归一化互功率谱

(1)

式中:Rfg为两图像相位相关的归一化互功率谱;Ff,Fg分别为f,g的傅里叶变换;Fg*为Fg的复数共轭。

相位相关法是求傅里叶逆变换峰值。对Rfg进行傅里叶逆变换，得到脉冲函数δ(x-x0,y-y0)，根据该函数的峰值可定位得到图像的位移坐标(x0,y0)。

(2)

1.2上采样矩阵乘法DFT

传统的利用相位相关法求取图像亚像素位移需借助上采样[8]，该过程在图像傅里叶变换(discreteFouriertransform，DFT)后的频率域进行上采样插零[22]，再进行相位相关法求取亚像素位移。在此基础上Soummer等提出基于矩阵乘法的傅里叶变换[19]，该方法对像素级位移位置一定邻域范围内的信息进行区域性上采样来求取亚像素位移，可高效率地求出图像间的亚像素位移。上采样矩阵乘法DFT计算可获得与相位相关上采样插零求取亚像素位移方法的同样效果[23]，得到图像的亚像素平移位置，而且计算量得到降低。

2改进的亚像素配准算法

2.1有效子图的优势

基于矩阵乘法的上采样离散傅里叶变换方法虽然避免了传统方法在求取图像亚像素位移时的不足，但该方法在利用相位相关求取整数级位移的步骤中其计算量会随着图像尺寸的增大而不断变大。为此，为了充分利用该方法亚像素配准的有效性又能使其适用于遥感影像的配准，这里提出采用有效子图代替原图进行图像亚像素配准的一种改进方法。

2.2有效子图的选取

有效子图可用二维小波方法来选取。二维小波分解后的低频分量代表了图像的轮廓信息，3个方向的高频部分分量代表了图像3个方向的细节信息，高频部分能量总和最大时对应的图像其细节部分信息最多，此时用该子图做图像配准其效果会较信息量少的子图要精确，以此作为有效子图选取标准。例如将大小为512×512的图像均匀分割成16等份。对16份有效子图分别进行一层二维小波变换如图1所示。

图1　二维小波分解

其中:LLi是第i个子图二维小波分解后的低频子图，HLi，LHi，HHi分别对应第i个子图二维小波分解水平、垂直、对角3个方向的高频子图。求取各子图高频总能量和：

(3)

式中：ENi为第i个子图3个方向高频能量总和，当采用16子图时i=1,2,3，…，16。HLi，LHi，HHi分别对应第i个子图二维小波分解水平、垂直、对角3个方向的高频子图。

2.3有效子图的亚像素配准

对每个子图高频总能量和的大小进行对比，取能量和最大时对应的子图作为有效子图。数学计算式：

(4)

式中：MAX为能量总和最大时对应的子图。ENi为各个子图的高频能量之和。

改进方法选取有效子图代替原图来进行配准的过程，与传统方法相比更加适用于大尺度遥感影像的高精度配准。后面的实验也会证实该改进方法在满足亚像素精度配准要求的前提下，较文献[13]中的相位相关法、文献[20]中的矩阵乘法DFT等方法都优越，能高效率进行图像亚像素配准。改进方法是将二维小波变换、相位相关、上采样矩阵乘法DFT相结合(wavelettransform,phasecorrelation,andmatrixmultiplyDFT)的亚像素图像配准算法，为了叙述简单以下简称WPM方法。

WPM算法具体步骤：

1)有效子图选取。利用原图等尺度分割后的各个子图进行二维小波分解，取高频能量总和最高时对应的子图作为下一步像素级粗定位的有效子图。

2)像素级粗定位。计算有效子图的相位相关归一化功率谱，求得图像间像素级位移(x0,y0)。

3)亚像素级定位。在像素级位移(x0,y0)周围进行k倍上采样矩阵乘法DFT计算，获得配准位置

(x0_Up,y0_Up)。

4)亚像素位移值。对像素级定位(x0,y0)与亚像素级定位(x0_Up,y0_Up)进行综合得最终亚像素配准结果(x0+ x0_Up/k,y0+y0_Up/k)。

2.4算法的效率分析

分析本文算法的计算复杂度。根据上采样矩阵乘法求取可得，e-2iπUXT的尺度为NB×NA，f(X,Y)的尺度为NA×NA，e-2iπYVT的尺度为NA×NB。根据复数运算中乘法需6个浮点运算，加法需2个浮点运算[24]，得总运算次数：

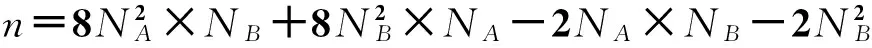
(5)

采样矩阵乘法DFT在配准过程中是以局部区域信息进行的亚像素配准，相比于传统基于傅里叶变换的零填充上采样插零而言，算法的计算复杂度已经大大缩小，而本文算法的计算复杂度要更优于上采样矩阵乘法DFT为(n/16)，故算法在计算量得到显著提高。

3实验结果及分析

为了验证算法的可行性与优越性，本文进行大量的对比试验、综合测试，并对实验结果进行分析。

3.1实验1

为了验证上述算法的优越性，进行第一组对比实验。计算平台是内存为4GB，处理器Core-i3，CPU主频1.8GHz的笔记本电脑，计算软件采用Matlab7.0。图像选取尺寸为512×512的Lena图像如图2(a)所示，实验用亚像素位移为△1(10.486，13.738)的图像如图2(b)所示，亚像素位移图像是通过傅里叶变换相位位移来实现的。

图2　实验图像

对图像进行16等分分割，每份子图大小为128×128，利用二维小波对各个子图进行分解,选取分解后3个高频分量总和最大时对应的子图作为有效子图。有效子图选取的结果如图3(a)、3(b)中高亮显示的子块所示，其中图3(c)为图3(a)高亮部分的放大，图3(d)为图3(b)高亮部分的放大。

图3　有效子图

选取上采样倍数k=100，分别用WPM算法、文献[13]和文献[20]中的方法对有效子图3(c)与3(d)进行配准，配准结果如表1所示。配准过程中WPM算法的归一化相位相关法像素级粗配准和矩阵乘法DFT亚像素级配准的频谱图分别如图4(a)、4(b)所示。

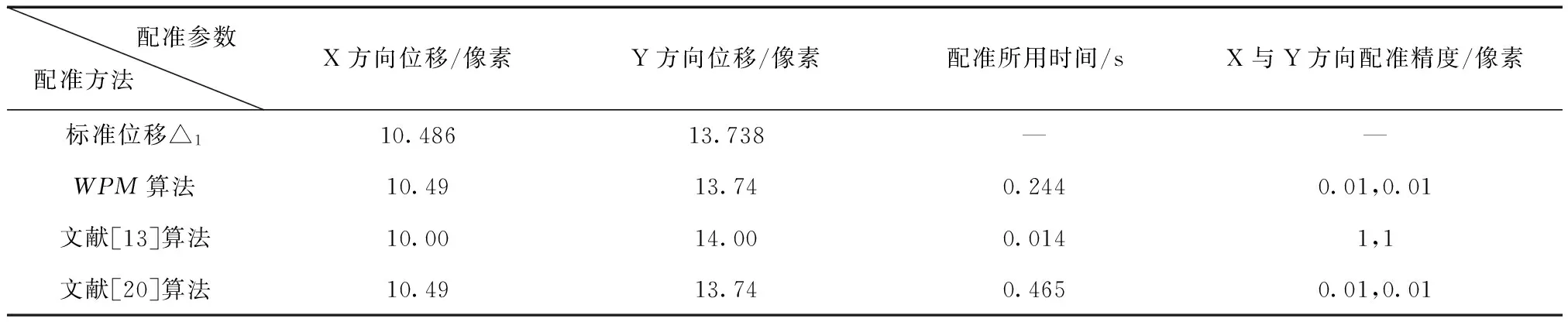
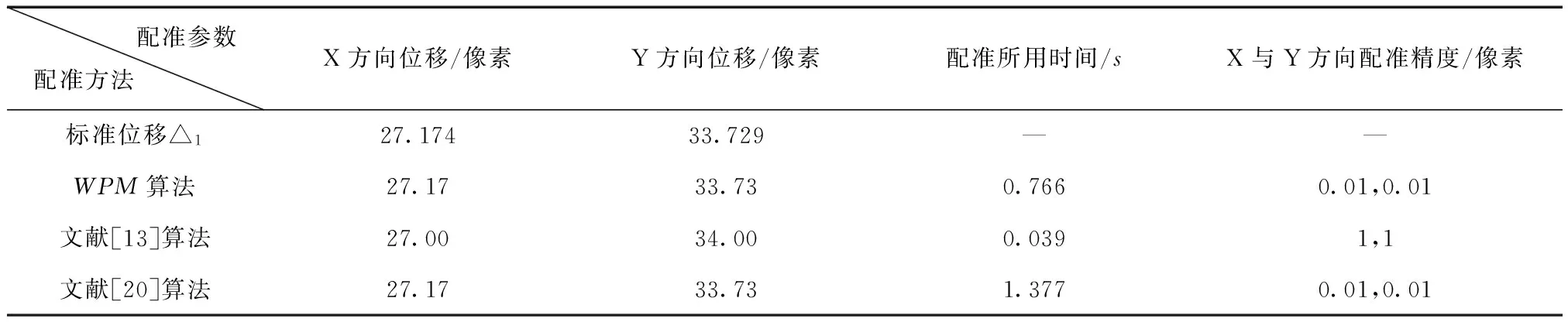
表1　不同方法的配准精度和速度对比

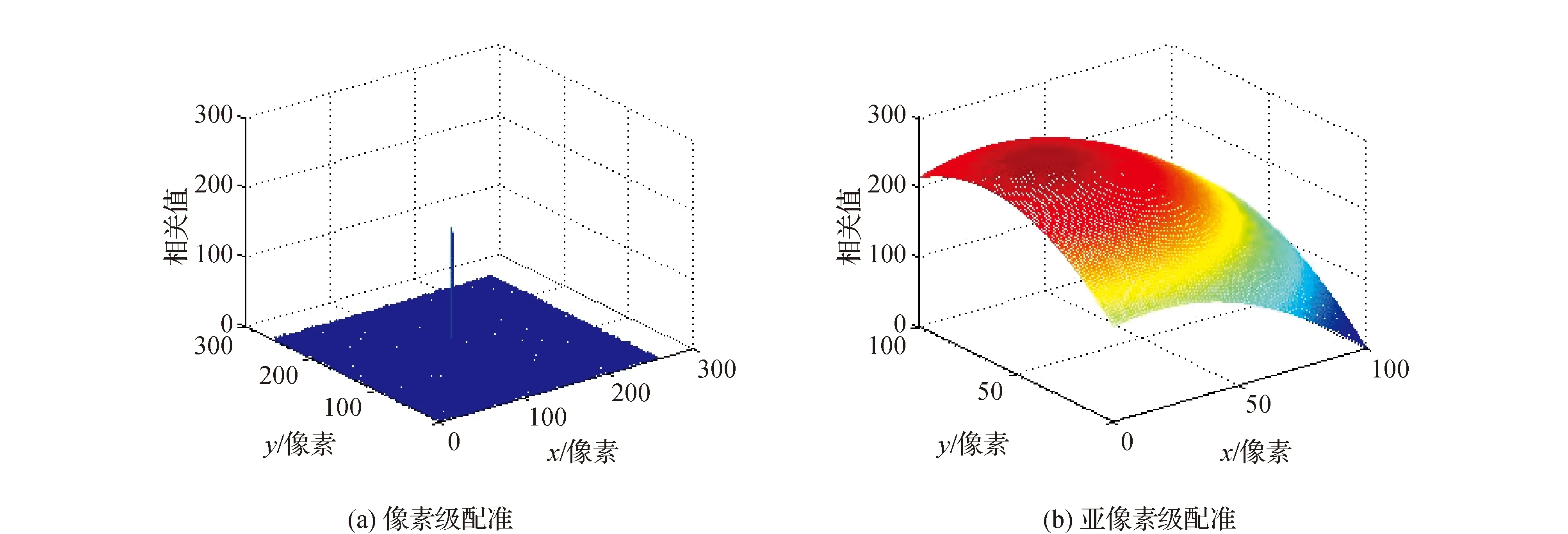
图4　图像的功率谱

从表1中可以看出WPM算法较文献[13]相位相关法相比，其配准精度达到0.01的亚像素精度能很好地满足亚像素配准的要求；WPM算法较文献[20]中上采样矩阵乘法DFT算法相比，在配准精度满足要求的同时，WPM算法的计算时间整整缩短一半，效率提高近一倍。仿真实验表明WPM算法能满足亚像素配准精度而且配准效率很高，可以很好地用于工程实践。

3.2实验2

为验证WPM算法工程实际应用的精确性与高效性，进行第二组实验。实验采用某地区上空的航拍遥感影像，从其中截取大小为1 024×1 024像素尺寸的影像如图5(a)所示，配准图像的位移为△2(27.173 6，33.729 1)，如图5(b)所示。

图5　某地区遥感影像

对此遥感影像同样进行16等分划分，各子图大小为256×256。有效子图的选取结果如图6(a)、6(b)中高亮显示的子块所示，图6(c)、6(d)分别为图6(a)、6(b)中高亮部分的放大。

图6　有效子图

上采样倍数k=100，采用WPM、文献[13]、文献[20]等算法对图6(c)与6(d)进行配准。WPM算法配准过程中像素级配准和亚像素级配准的频谱图分别如图7(a)、7(b)所示。各方法亚像素配准结果如表2所示。

通过图7可得，改进方法用于真实遥感影像像素级及亚像素级定位时仍具有唯一性与精确性。通过表2可得WPM算法用于真实遥感影像的亚像素配准时，与文献[13]方法相比较，仍能得到高精度的亚像位移；WPM算法与目前亚像素配准精度较高的上采样矩阵乘法DFT相比，精度在满足要求的同时，计算速度几乎快了一倍。

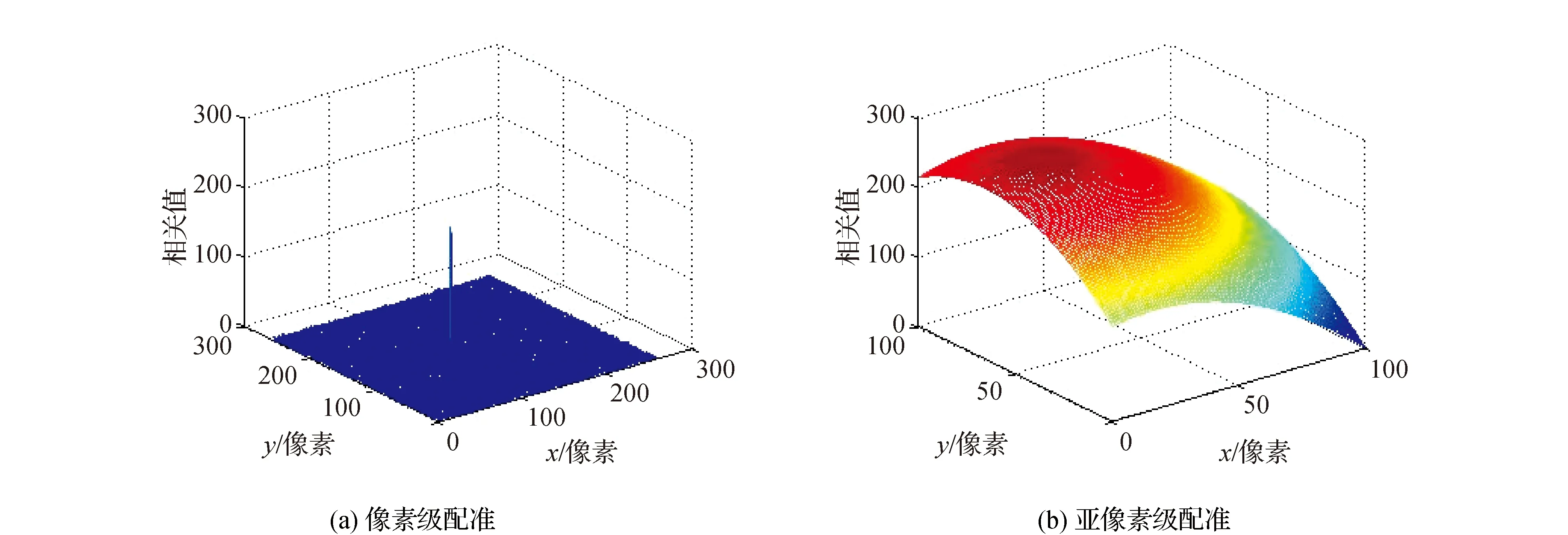
图7　图像的功率谱

配准参数 配准方法 X方向位移/像素Y方向位移/像素配准所用时间/sX与Y方向配准精度/像素标准位移△127.17433.729——WPM算法27.1733.730.7660.01,0.01文献[13]算法27.0034.000.0391,1文献[20]算法27.1733.731.3770.01,0.01

3.3实验3

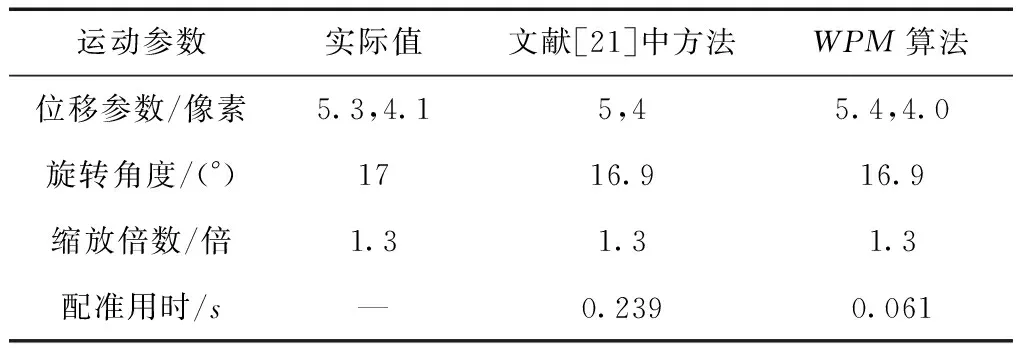
为验证改进方法的普遍适用性，进行第3组对比试验。实验选取256×256的遥感图像8(a)作为参考，对其进行参数分别为(5.3，4.1，17，1.3)的位移、旋转、缩放处理，获得待配准的图像如图8(b)所示。图8是整图根据配准参数的配准结果。表3列出了本文WPM方法与文献[21]中传统方法的对比结果。

图8　实验影像

运动参数实际值文献[21]中方法WPM算法位移参数/像素5.3,4.15,45.4,4.0旋转角度/(°)1716.916.9缩放倍数/倍1.31.31.3配准用时/s—0.2390.061

通过以上实验结果表明本文方法在影像间同时存在旋转、缩放、平移变换时同样适用。

4结论

本文提出了一种利用有效子图代替原图进行配准的改进方法，在保证图像间高精度亚像素配准准确性的前提下同时提高配准的速度，减少配准过程的计算量，适用于存在旋转、缩放、平移的遥感数据处理。

参考文献：

[1]李德仁.利用遥感影像进行变化检测[J].武汉大学学报(信息科学版),2003,28(增1)：7-12.

[2]冯志元,李朝奎,殷智慧,等.基于集群的遥感影像并行绘制研究[J].测绘工程,2014,23(7):26-29.

[3]孙涛,林立宇,孙夫雄,等.光学遥感影像复原与超分辨重建[M].北京：国防工业出版社,2012.

[4]陈令羽,贾奋励,宋国民.基于全景影像的增强地理现实配准方法研究[J].测绘工程,2014,23(10)：4-8.

[5]朱朝杰,王仁礼,董广军.MATLAB环境下遥感影像配准与融合技术研究[J].测绘工程,2006,15(06)：57-59.

[6]TIANQ,HUHNSMN.Algorithmsforsubpixelregistration[J].ComputerVision,Graphics,andImageProcessing,1986,35(2) 220-233.

[7]刘卫光,崔江涛,周利华.插值和相位相关的图像亚像素配准方法[J].计算机辅助设计与图形学学报,2005,17(6)：1273-1277.

[8]FOROOSHH,ZERUBIAJB,BERTHODM.Extensionofphasecorrelationtosubpixelregistration[J].IEEETransactionsonImageProcessing,2002,11(3)：188-200.

[9]THEVENAZP,RUTTIMANNUE,UNSERM.Apyramidapproachtosubpixelregistrationbasedonintensity[J].IEEETransactionsonImageProcessing,1998,7(1) 27-41.

[10] 李畅,李芳芳.基于假设检验的数字影像线状特征亚像素自动提取[J].测绘学报,2013,42(1)：67-72.

[11] 李延成,李军,刘慧霞,等.基于最小二乘法的区域整体最优匹配选取控制点的方法[J].测绘科学,2012,37(6)：94-97.

[12] 黎俊,彭启民,范植华.亚像素级图像配准算法研究[J].中国图像图形学报,2008,13(11)：2070-2075.

[13]KUGLINCD.Thephasecorrelationimagealignmentmethod[C].Proc.Int.Conf.onCyberneticsandSociety,1975:163-165.

[14] 高莹莹,杨建峰,马晓龙,等.基于Fourier-Mellin算法的干涉图像配准[J].光学精密工程,2007(9):1415-1420.

[15]LEEDJ,MITRAS,KRILETF.Analysisofsequentialcompleximages,usingfeatureextractionandtwo-dimensionalcepstrumtechniques[J].JOSAA,1989,6(6)：863-870.

[16]DECASTROE,MORANDIC.RegistrationoftranslatedandrotatedimagesusingfiniteFouriertransforms[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1987 (5)：700-703.

[17]CHENQ,DEFRISEM,DECONINCKF.Symmetricphase-onlymatchedfilteringofFourier-Mellintransformsforimageregistrationandrecognition[J].IEEETransactionsonPatternAnalysisandMachineIntelligence,1994,16(12)：1156-1168.

[18]REDDYBS,CHATTERJIBN.AnFFT-basedtechniquefortranslation,rotation,andscale-invariantimageregistration[J].IEEETransactionsonImageProcessing,1996,5(8)：1266-1271.

[19]SOUMMERR,PUEYOL,SIVARAMAKRISHNANA,etal.FastcomputationofLyot-stylecoronagraphpropagation[J].OpticsExpress,2007,15(24)：15935-15951.

[20]GUIZAR-SICAIROSM,THURMANST,FIENUPJR.Efficientsubpixelimageregistrationalgorithms[J].Opticsletters,2008,33(2)：156-158.

[21] 李忠新,茅耀斌,王执铨.基于对数极坐标映射的图像拼接方法[J].中国图像图形学报,2005,10(1)：59-63.

[22]SMITHJO.MathematicsoftheDiscreteFourierTransform(DFT)：Withmusicandaudioapplications[M].JuliusSmith,2007.

[23] 周武,胡跃明.基于相位相关和重采样的亚像素图像配准算法[J].华南理工大学学报(自然科学版),2010,38(10)：68-73.

[24] 王彩玲,程勇,赵春霞,等.局部相位相关用于图像亚像素级配准技术研究[J].中国图像图形学报,2011,16(3)：427-432.

[责任编辑：李铭娜]

A fast sub-pixel registration method for remote sensing image

ZHOU Jinghong,ZHU Jianjun,ZHOU Cui,FAN Donghao

(SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China)

Abstract：A fast and efficient sub-pixel registration method is proposed in order to solve the classical methods’ problems of low efficiency.This paper uses the efficient sub-graph instead original image to sub-pixel registration,based on the Fourier transform phase correlation and matrix Fourier transform method.Effective sub-graph is selected by the total size of the high-frequency energy after two-dimensional wavelet decomposition,then the phase correlation is used to calculate the pixel shift and matrix Fourier transform to calculate the sub-pixel shift.Not only the improved method inherits the advantage of matrix Fourier transform sub-pixel registration,but also the registration speed is greatly improved.This is more applicable to massive remote sensing data.Through simulation and engineering practice,the composited registration accuracy and speed,prove that the improved method is more efficient compared with the classical methods,and more suitable for real remote sensing image registration.

Key words：sub-pixel registration；effective sub-graph；phase correlation；normalized cross power spectrum；matrix direct Fourier transform；Fourier-Mellin transform

DOI:10.19349/j.cnki.issn1006-7949.2016.07.015

收稿日期：2015-05-20

基金项目：973子课题(2013CB733303)；国家863资助项目(2012AA121301)；国家自然科学基金资助项目(41274010)

作者简介：周靖鸿(1989-)，男，硕士研究生.

中图分类号：TP752

文献标识码：A

文章编号：1006-7949(2016)07-0071-07