基于SGP4模型与多普勒频移的改进定轨方法

陆正亮, 张　翔, 刘　洋, 廖文和

(南京理工大学机械工程学院, 江苏 南京 210094)



基于SGP4模型与多普勒频移的改进定轨方法

陆正亮, 张翔, 刘洋, 廖文和

(南京理工大学机械工程学院, 江苏 南京 210094)

摘要：立方体卫星广泛使用两行根数(two-line element, TLE)结合SGP4模型作为定轨的唯一或是备份手段。针对SGP4模型长期预报误差积累的问题,分析了模型的误差来源及分布情况,提出两种利用地面观测站测量多普勒频移提高定轨精度的方法。一种方法直接修正大气阻力项系数,结果表明能大幅减小速度方向上的预报误差,将预报10天的位置精度提高到4 km以内。另一种方法将已知的两行根数更新为卫星过境时刻的两行根数,然后修正纬度幅角,修正后短期预报误差能基本消除但长期精度不如前一种方法。通过对在轨立方体卫星的实际测量也验证了上述的结论。

关键词：立方体卫星; 两行根数; SGP4模型; 多普勒频移

0引言

从1999年立方体卫星的概念被提出以来,世界范围内的高校、研究所以及商业航天机构都在深入挖掘立方体卫星的应用潜能,共同推动了立方体卫星研制技术的跨越式发展。立方体卫星的测定轨手段除了使用GPS接收机或应答机以外,还大范围使用SGP4轨道递推模型进行定轨。目前在轨的立方体卫星大多依赖北美防空司令部(North American Aerospace Defense Command,NORAD)发布的两行根数结合SGP4模型进行定轨[1-5]。但是NORAD发布两行根数的周期是不确定的,容易导致定轨误差随时间大量累积。为此国内外学者研究了多种生成两行根数的算法[6-9],但其大多以GPS精密星历为测量数据,并不适用于立方体卫星的轨道确定。

卫星与地面站通信时发生的多普勒频移现象与卫星轨道以及地面站的相对位置之间存在对应关系,美国海军导航系统NNSS就是基于这个原理建立的第一代卫星导航系统。立方体卫星使用的通信频段以业余波段UHF/VHF为主,大多数高校或研究机构在研制立方体卫星时都会配套建立一个业余频段地面站,使得多普勒频移成为研究人员对立方体卫星自主测轨的一种低成本手段。文献[10]基于J2模型提出利用多普勒频移测量得到卫星位置速度信息的方法,在卫星过境期间得到不错的定轨精度,但其可行性的基础是在全球建立地面站网络以缩短卫星过境时间间隔,从而避免使用J2模型进行长期轨道预报。

将多普勒频移测量与SGP4模型相结合能解决卫星过境时刻外的轨道预报精度问题。文献[11]对多普勒频移测量数据拟合两行根数的算法原理以及性能进行了研究,结果发现算法难以收敛至正确结果。认真分析多普勒频移测量量与轨道根数之间的本质联系可得出两方面原因,其一是多普勒频移与某些轨道根数之间的关系不够紧密导致算法的收敛半径过小;另外由于多普勒频移测量数据的时间跨度太短而不足以去除轨道摄动中大气阻力和重力的长期项影响,从而导致拟合得到的两行根数的精度过低。

本文结合多普勒频移这类测量量的本质特性以及SGP4模型的误差分布情况,认为多普勒频移测量是提高SGP4模型定轨精度的一种高效而且低廉的手段。提出了两种利用多普勒频移测量修正两行根数的方法,对其可行性进行了仿真分析,并利用LabView软件平台搭建的地面数据采集系统进行了实际测量验证。

1多普勒频移

卫星过境地面站时两者之间的相对速度会发生改变,使得地面站接收到卫星发送的信号频率发生偏移,这就是所谓的多普勒频移现象。理论上来说多普勒频移与卫星轨道根数之间是一一对应的关系,使得多普勒频移成为卫星测轨或是实现卫星导航的一种有效测量方式。但在实际应用中使用该方法定轨和导航的精度并不高,现代卫星基本已经不再使用这种测量方式。而对于发展迅速的立方体卫星来说,中等定轨精度已经能够满足其需求,测量便捷成本低廉的多普勒频移成为立方体卫星实现自主测轨的方式之一[12]。

(1)

式中,C表示光速;i表示测量次数;f0表示卫星的发射频率;fi表示地面站接收到的频率。

使用多普勒频移定轨,了解并建立准确的测量模型甚为关键。卫星与地面站之间的距离变化率这类测量量与轨道根数的关系较为复杂,不便使用解析表达式来表达。通过分析距离变化率与轨道根数之间的内在联系可以了解多普勒频移测量的本质特性。假设地球停止自转,距离变化率就只与轨道形状、卫星位置以及地面站到星下点的垂直距离相关,而与决定轨道位置的倾角和升交点赤经无直接关系。如图1所示,当图1中d1和h1分别与d2和h2相等时,纵使卫星1和卫星2有着不同的轨道倾角和升交点赤经,计算得到的距离变化率也是相同的。正是由于地球自转才使得倾角和升交点赤经与距离变化率关联在一起。但由于地球自转相对卫星运动来说速度太慢,使得这种关联非常不紧密,加上多普勒频移测量误差以及测量模型误差的影响，必然导致使用多普勒频移直接定轨的精度不高。

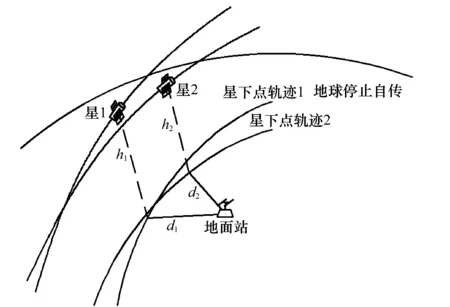
图1　卫星与地面站之间的相对位置

2两行根数与SGP4模型的误差分析

两行根数(two-lineelement,TLE)是北美防空司令部基于一般摄动理论产生的用于预报地球轨道飞行器位置和速度的一组轨道根数。与利用测轨数据进行轨道确定或轨道预报获得的瞬时轨道六根数不同,两行根数是在真赤道、平春分点坐标系下的“平均”根数,是一种利用特定的方法去除了周期摄动力影响后的轨道根数,通常与SGP4、SDP4模型一起使用。SGP4模型是一种空间目标解析预报模型,当使用特定的TLE作为输入时可较准确的对近地目标轨道进行预报,计算量较小且精度适中。SGP4模型的原理就是在TLE的基础上通过重构短、长周期项以及长期项的摄动力大小从而对轨道进行预报。使用SGP4模型预报轨道的误差会随着时间累积越来越大,提高轨道预报精度的前提则是分析清楚SGP4模型的误差来源以及误差分布情况。

预报误差来源包括输入的TLE误差以及摄动力建模误差。摄动力建模误差是SGP4模型的固有误差无法消除,TLE误差则来源于用于拟合TLE的测量数据误差以及相关拟合算法误差。但是北美防空司令部发布两行根数的同时并没有公布其误差信息,这给评估SGP4模型的预报精度带来了一些困难。本文借助卫星工具包(satellitetoolkit,STK)软件的强大仿真能力来分析SGP4模型的误差分布情况。

首先使用高精度轨道预报(high-precisionorbitalpropagator,HPOP)精确轨道递推模型生成一条近地轨道模拟真实轨道。然后使用STK软件自带的GenerateTLE工具拟合出两行根数来仿真北美防空司令部发布的TLE,拟合算法用到的测量数据是真实轨道的位置信息。最终利用拟合得到的TLE建立一条SGP4预报轨道。通过比较真实轨道和预报轨道的位置关系可以分析SGP4模型的误差分布情况。预报误差以位置偏差的3个分量,即速度方向偏差、垂直轨道面方向偏差以及轨道半径方向偏差来描述。研究发现拟合TLE的时长是决定SGP4模型误差的最主要因素,由于这里研究的重点是误差分布情况,故将拟合时长设置为北美防空司令部发布TLE的平均周期1.5d。模拟的真实轨道高度为500km,得到的典型结果如图2所示,图2中横坐标0天表示所发布TLE的历元时间。

图2　SGP4轨道预报精度

由图2可见,SGP4模型的预报误差主要集中在速度方向偏差上,预报5 d的速度方向偏差为-18 km,预报10 d则为-35 km。而垂直轨道面方向偏差以及轨道半径方向预报精度较高,预报15 d的偏差范围在±1.5 km以内。结果与国外一些学者采用精密星历对比法得出的结论类似[13-16]。

分析低地球轨道卫星的轨道摄动力来源可知,大气阻力是影响位置误差中速度方向偏差的最主要来源。在TLE中代表大气阻力摄动的是大气阻力项系数B*。由此推论拟合得到的TLE中B*的误差可能是造成速度方向偏差较大的原因。可以通过简单改变B*的大小来验证这个推论。图2中使用的TLE中B*的大小为0.000 152 32,当将B*更改为0.000 182 32时得到的轨道预报精度结果如图3所示。图3中改变B*后预报10 d的速度方向偏差由-35 km变化为10 km,验证了上述的推论。

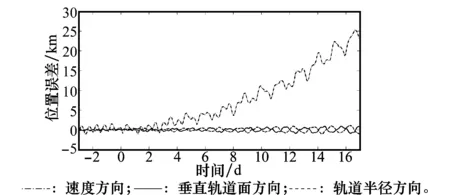
图3　调整B*后的SGP4轨道预报精度

如果通过某种测量手段能修正速度方向的偏差,同时又能保持垂直轨道面方向以及轨道半径方向的高精度,将大大提高立方体卫星利用SGP4模型定轨的精度。

3修正TLE与仿真分析

依据上述对多普勒频移测量特性以及SGP4模型预报轨道的误差特性的分析,不难看出多普勒频移是一种能高效提高SGP4模型定轨精度的方法,而且成本低廉,其唯一需要的测量工具是一台实验室通用仪器——频谱分析仪。

大气阻力项系数B*的误差是造成速度方向偏差的主要因素,而在轨道六根数中描述速度方向偏差的则是纬度幅角误差。现提出两种利用多普勒频移测量提高定轨精度的方法如下。

3.1修正大气阻力系数

(2)

(3)

由于距离变化率与状态量B*之间是非线性的关系,采用解析方法计算导数矩阵是非常困难的,可以使用有限差分的方法来计算导数矩阵，即

(4)

式中,ΔB*为小量,ΔB*大小的正确选择是保证有限差分法计算精度的关键所在。设定一系列大小有序的ΔB*值来计算Ai的大小,从而得到SGP4模型对变量ΔB*的线性范围,部分结果如图4所示。

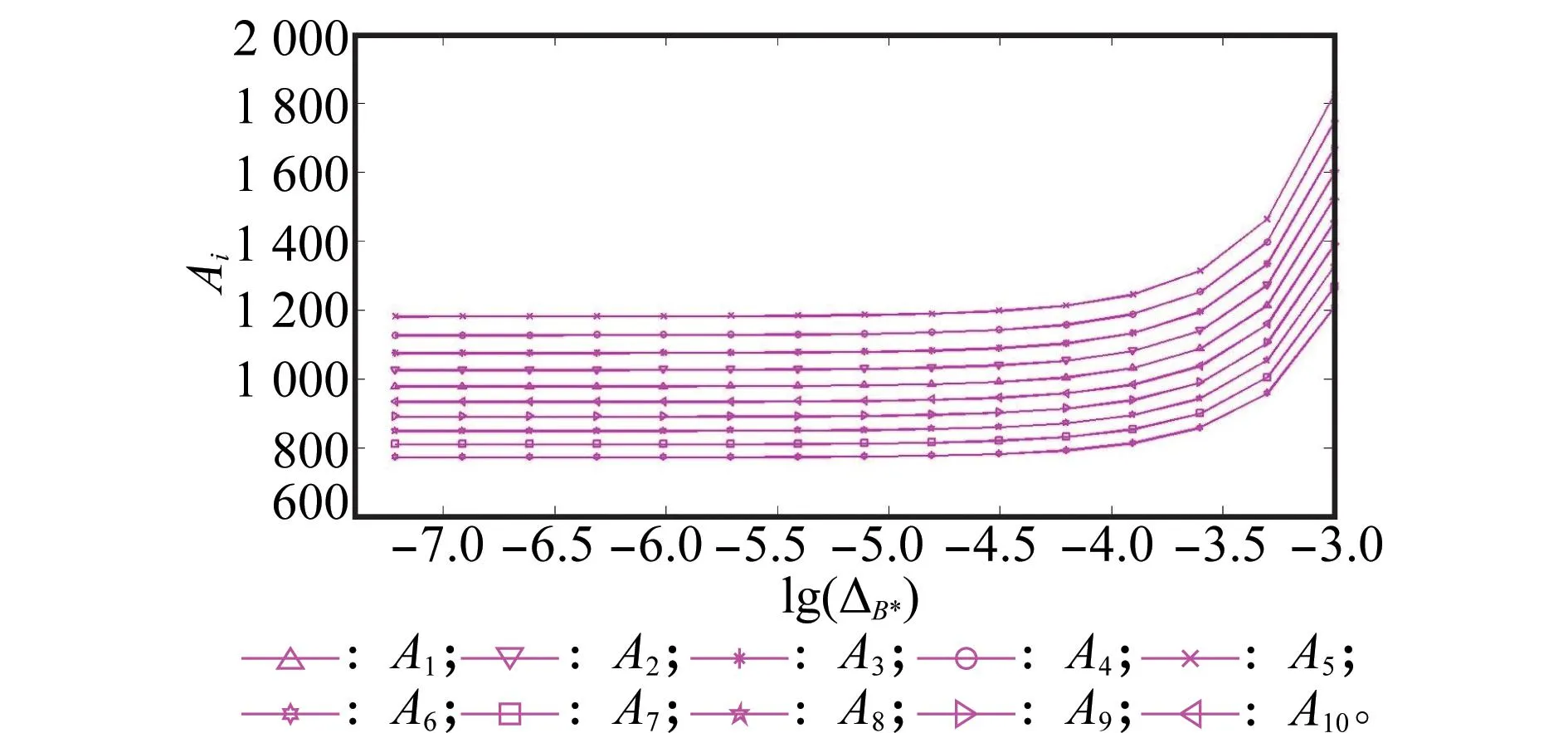
图4　偏导数Ai随小量ΔB*的变化曲线

图4显示当ΔB*选为10-5时导数Ai趋于线性,因此设定ΔB*为10-5。由此得到B*修正量的公式为

(5)

算法收敛的条件是残差的均方根值小于某一阈值或是不再变化。残差的均方根计算公式为

(6)

3.2修正纬度幅角

利用已知TLE的预报轨道信息可以直接拟合更新得到卫星过境地面站时刻的平均轨道根数,由于拟合过程不存在模型误差的差异,更新后TLE的预报轨道与更新前TLE的预报轨道是完全一致的,但卫星过境时刻的轨道预报误差来源却发生了变化。更新前的轨道预报误差主要是由于大气长期摄动作用的结果,所以TLE的误差来源主要是大气阻力项系数误差;而更新后TLE的历元时间为卫星过境时刻,基本消除了大气摄动对轨道预报误差的影响,TLE的误差来源主要是是纬度幅角误差。利用多普勒频移测量修正纬度幅角即可提高轨道预报精度。更新后的TLE为

(7)

纬度幅角是近地点幅角与真近点角相加得到

(8)

TLE中表征纬度幅角的变量是ωo和Mo,同样利用最小二乘估计算法对这两个参数进行修正,此时状态向量为

(9)

其余计算过程与第3.1节类似。

3.3仿真分析

Shakespeare wrote comedies（喜剧）with happy endings（美满的结局），like A Midsummer Night’s Dream（《仲夏夜之梦》）.He wrote tragedies（悲剧）with sad endings，like Romeo and Juliet（《罗密欧与朱丽叶》）.He wrote about 38 plays，maybe more.

利用Matlab软件结合STK对上述两种修正方法进行仿真验证。仿真使用的真实轨道为第3小节使用的标称轨道,仿真时间选为两行根数历元时刻5d后的某次过境时刻,由图2可见速度方向偏差大约在20km。初始的TLE与拟合更新后的TLE分别标记为TLE0和TLE1,具体形式如表1所示。

表1　仿真使用的两行根数

仿真的实际距离变化率测量值由真实轨道计算并加上测量白噪声得到,而估计测量值由SGP4预报轨道计算而来。为获得较高的拟合精度,仿真参数参考真实多普勒频移测量系统的测量性能,即仿真步长设置为2 s,仿真时间为7.5 min。实际测量值与估计测量值曲线如图5所示。首先使用实际测量值与仿真测量值的残差来修正大气阻力项系数B*,算法迭代4次后收敛到0.000 177 75。修正后的TLE的预报轨道误差如图6所示。然后仿真分析修正纬度幅角的方法。修正后ωo和Mo分别为179.115°和311.755°,修正后的TLE的预报轨道误差如图7所示。

图5　实际测量值与估计测量值(仿真)

图6　修正B*后的SGP4轨道预报精度(仿真)

由图6可见,修正B*参数后卫星过境时刻的轨道预报精度由20 km提高到2 km左右,预报至第10 d的精度也达到4 km。图7中修正纬度幅角后卫星过境时刻的精度也提升至2 km,但预报10 d(从修正前两行根数历元时刻起计算)的精度仍然在25 km左右。由此可见利用多普勒频移测量数据修正两行根数的方法能及时修正SGP4模型随时间累积较大的速度方向误差分量,能大大提高SGP4预报轨道的精度;两种修正方法在短期内对于精度的提高相差不大,但对于长期精度来说修正B*的方法明显优于修正纬度幅角的方法。

图7　修正纬度幅角后的SGP4轨道预报精度(仿真)

4实际多普勒频移数据的测量

4.1自动数据采集系统

使用UHF/VHF频段地面站与频谱分析仪来测量在轨微小卫星的多普勒频移现象,系统硬件架构如图8所示。图8中GPS接收机用于给工控计算机授时以保证时间系统的统一,频谱仪通过LAN口与工控计算机进行通信,实现远程控制与自动数据采集。上位机采用LabView软件对频谱仪捕获的卫星信号进行分析存储。

由于大部分卫星信号在时间上不是连续发送的,导致采集到的数据会有大量背景噪声存在,自动数据采集系统程序中通过以下3种途径有效去除背景噪声数据,设定的采样周期为1 s。

(1) 提前采集背景噪声信号强度的最大值,并加上2 dBm余量,测量时以此为阈值剔除任何小于此阈值的信号;

(3) 采用曲线拟合的方法剔除剩余少量噪声信号。

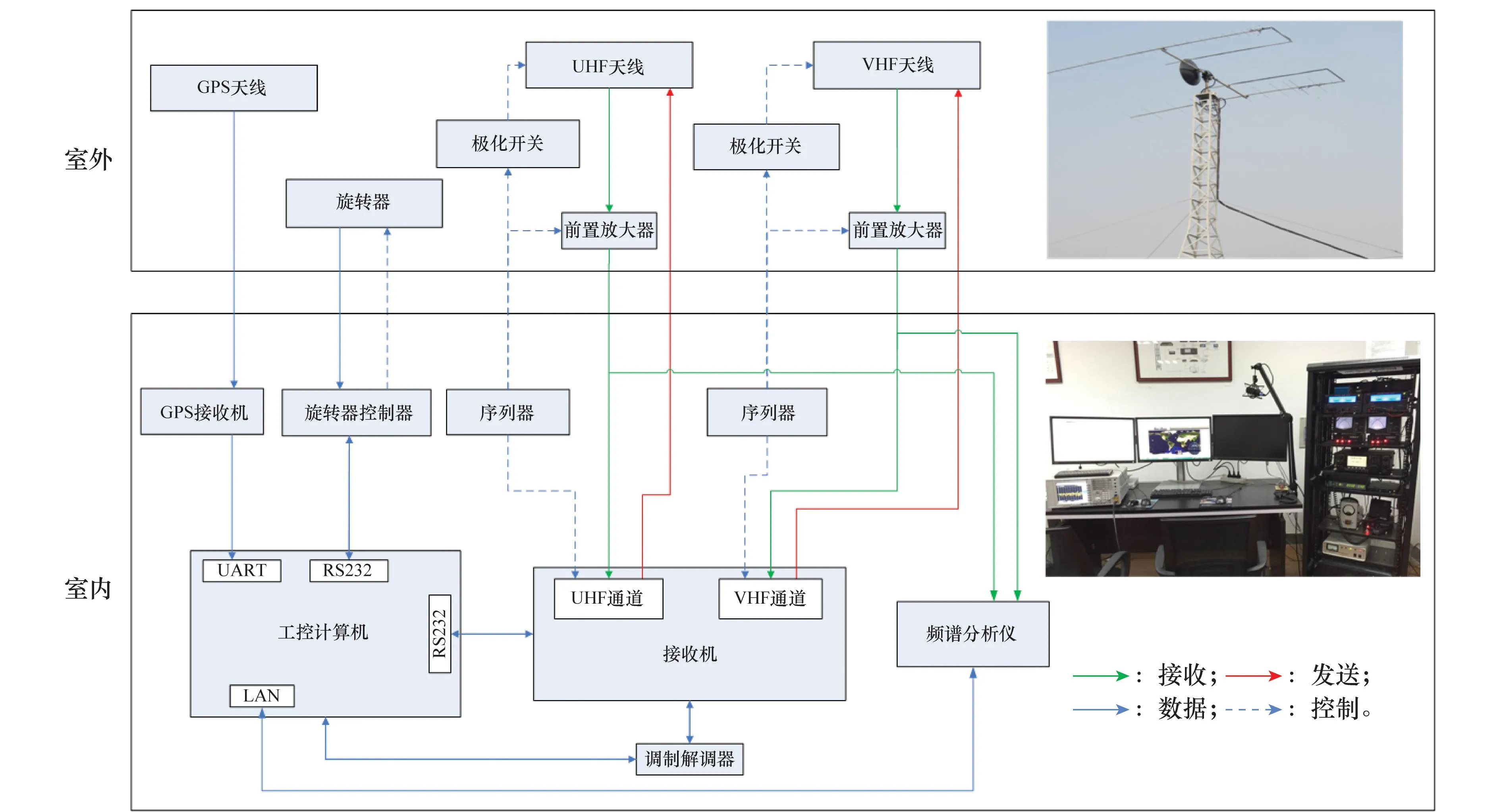
图8　多普勒频移测量系统硬件架构

自动数据采集系统工作过程如下:

(1) 在卫星过境前10分钟内录制带宽为10 kHz(能完全覆盖卫星过境时间内的中心频率漂移)大小的背景噪声信号,并得出噪声信号强度的最大值;

(2) 当地面站指向卫星仰角大于5°时,开始实时跟踪卫星信号,当信号强度大于噪声信号最大值+2 dBm时,则认为此信号有效并记录下来;

(3) 在得到足够数据点后快速利用最小二乘拟合算法计算出B*的大小并及时以上行指令的方式上行至卫星。

上位机编写的程序界面如图9所示。

图9　多普勒频移自动数据采集系统界面

4.2发射频率常值漂移的补偿

(10)

(11)

(12)

这样得到实际发射频率的估计值为

(13)

4.3对QB50 P1卫星实测数据的分析

QB50P1立方体卫星是2014年6月发射入轨的QB50项目先导星。本文对其多普勒频移信号连续观测了数周,由于缺乏所观测卫星的实时在轨位置信息,无法对所提出的改进定轨方法的误差大小进行直观比较,故在下文中使用多普勒频移测量值这一间接量对定轨精度进行间接分析,如修正后的两行根数相对原始两行根数预报的多普勒频移计算值更接近真实多普勒频移测量值,则认为修正后的两行根数提高了轨道预报精度。现将一组典型的测量与分析的结果展示如下。

2015年1月24日发布的TLE标记为TLE0,1月29日观测到的多普勒频移测量数据转换为距离变化率后如图10所示,图10中显示采用自动数据采集系统测量得到的多普勒频移曲线较为平滑。利用观测到的多普勒频移测量值分别应用修正B*的方法与修正纬度幅角的方法对两行根数进行更新,更新后的两行根数分别标记为TLE1与TLE2,表2所示为3组TLE的具体数值。由于NORAD发布TLE的周期为1～3d,为对修正后两行根数的短期和长期预报精度进行评估,分别选取了1月30日和2月2日的观测数据进行分析。图11和图12所示的分别为1月30日与2月2日的观测数据,图中黑色圆点为测量到的实际距离变化率,红色曲线为原始两行根数TLE0计算出的估计距离变化率,紫色和绿色曲线分别为B*和纬度幅角修正后的TLE1和TLE2计算出的估计距离变化率。

表2　实际测量使用的两行根数

图10　多普勒频移1月29日测量数据

图11　多普勒频移1月30日测量数据

观察图11可知,更新后的TLE1和TLE2都比TLE0更接近实际多普勒频移测量值,表明两种修正TLE的方法都能使SGP4模型短期轨道预报精度得到大幅提升;图12显示TLE2在估计2月2日的多普勒频移曲线时明显没有TLE1精确,表明修正纬度幅角的方法用于长期轨道预报会带来较大误差。

图12　多普勒频移2月2日测量数据

5结 论

本文通过对多普勒频移这类测量量本质属性的探索以及对SGP4模型预报误差分布的分析,总结出多普勒频移测量是一种能高效提高SGP4模型预报精度的方式。结合两行根数的误差来源提出了修正B*以及修正纬度幅角两种方法。通过仿真以及对实际观测数据的分析验证了这两种方法的可行性。在精度方面,两种方法在短期预报时都能快速提高SGP4模型预报精度,但在长期预报时修正B*的方法明显优于修正纬度幅角的方法。

参考文献：

[1] Vallado D A, Crawford P, Hujsak R, et al. Revisiting spacetrack report #3[C]∥Proc.oftheAIAA/AASAstrodynamicsSpecialistConference, 2006.

[2] Han L, Chen L, Zhou B Z. Precision analysis of SGP4/SDP4 implemented in space debris orbit prediction[J].ChineseSpaceScienceandTechnology, 2004, 24(4): 65-71. (韩蕾,陈磊,周伯昭. SGP4/SDP4模型用于空间碎片轨道预测的精度分析[J].中国空间科学技术,2004,24(4):65-71.)

[3] Vallado D A, Crawford P. SGP4 orbit determination[C]∥Proc.oftheAIAA/AASAstrodynamicsSpecialistConferenceandExhibit, AIAA-2008-6770.

[4] Zhang T, Chen R L, Chen H W, et al. Conversion of the non-cooperative space object using bearing-only measurements[J].ActaPhotonicaSinica, 2009, 38(12): 3230-3234. (张涛,陈荣利,程洪玮, 等. 空间目标TLE天基光学混合状态SPKF拟合方法[J].光子学报,2009,38(12):3230-3234.)

[5] Baranov I V. SGP4 propagation program design and validation[D]. Saint-Hubert: University of Waterloo, 2009.

[6] Montenbruck O, Gill E. Real-time estimation of SGP4 orbital elements from GPS navigation[C]∥Proc.oftheInternationalSymposiumSpaceFlightDynamics, 2000.

[7] Greene M R, Zee R E. Increasing the accuracy of orbital position information from NORAD SGP4 using intermittent GPS readings[C]∥Proc.ofthe23rdAnnualAIAA/USUConferenceonSmallSatellites, SSC09-X-7.

[8] Zhu H X, Peng B B, Ju T. Determination of two-line elements with numerical method[J].GeomaticsandInformationScienceofWuhanUniversity,2009,34(9):1113-1115.(朱洪欣,彭碧波,巨涛. 利用数值法获取两行根数[J].武汉大学学报(信息科学版),2009,34(9):1113-1115.)

[9] Andersen D E. Computing NORAD mean orbital elements from a state vector[D]. Ohio: Air Force Institute of Technology, 1994.

[10] Sakamoto Y, Kasahara Y, Yasaka T. Low-cost orbit determination system for a CubeSat[C]∥Proc.oftheInternationalCubeSatSymposium, 2003.

[11] Hsu C, Koh D, Rahman O A, et al. Low-cost rapid TLE updating method for nano-satellites using Doppler signature[C]∥Proc.oftheAIAASpaceConference&Exposition, 2011.

[12] Weeks C J, Buschelman A, Sabillo R. Direct determination of a spacecraft orbit from the Doppler data signature[J].TheJournaloftheAstronauticalSciences, 1999, 47(3/4): 295-308 .

[13] Flohrer T, Krag H, Klinkrad H. Assessment and categorization of TLE orbit errors for the US SSN catalogue[C]∥Proc.ofthe5thEuropeanConferenceonSpaceDebris, 2009.

[14] Kelso T S. Validation of SGP4 and IS-GPS-200D against GPS precision ephemerides[C]∥Proc.ofthe17thAAS/AIAASpaceFlightMechanicsConference, 2007.

[15] Oltrogge D L, Ramrath J. Parametric characterization of SGP4 theory and TLE positional accuracy[C]∥Proc.ofthe22ndAnnualAIAA/USUConferenceonSmallSatellites, SSC08-X-13.

[16] Gangestad J W, Hardy B S, Hinkley D A. Operations, orbit determination, and formation control of the aerocube-4 CubeSats[C]∥Proc.ofthe27thAnnualAIAA/USUConferenceonSmallSatellites, SSC 13-X-4.

[17] Capderou M.Satellitesorbitsandmissions[M]. France: Springer-Verlag, 2005.

[18] Vallado D A.Fundamentalsofastrodynamicsandapplications[M]. Hawthorne, CA : Springer/Microcosm, 2007.

[19] Lam Q M, Junker D, Anhalt D, et al. Analysis of an extended Kalman filter based orbit determination system[C]∥Proc.oftheAIAAGuidance,Navigation,andControlConference, 2010.

[20] Levit C, Marshall W. Improved orbit predictions using two-line elements[J].AdvancesinSpaceResearch, 2011, 62(7): 1107-1115.

陆正亮(1990-),男,博士研究生,主要研究方向为微小卫星轨道姿态测量与控制。

E-mail:112010115@njust.edu.cn

张翔(1973-),男,副教授,博士,主要研究方向为微小卫星总体技术。

E-mail:zhxiang2002@126.com

刘洋(1991-),男,硕士研究生,主要研究方向为微小卫星姿态传感器设计、测试与标定。

E-mail:513101001254@njust.edu.cn

廖文和(1965-),男,教授,博士,主要研究方向为微小卫星总体应用技术。

E-mail:cnwho@mail.njust.edu.cn

Improved orbit determination based on SGP4 model and Doppler shifts

LU Zheng-liang, ZHANG Xiang, LIU Yang, LIAO Wen-he

(SchoolofMechanicalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

Abstract:CubeSats always choose two-line element (TLE) in conjunction with the SGP4 model to determine the orbit, or as a backup method. To settle the problem that the propagation error accumulates over time, the source and distribution of the errors are analyzed and two improved approaches are proposed by using Doppler shifts. One is to directly correct the drag coefficient and results show a significantly decrease in in-track orientation error. The position difference is improved to 4 km in 10 days. The other approach is to update the TLE epoch time to the pass time firstly, and then correct the argument of the latitude. Simulation results indicate that the position error can be almost removed in a short time but the long time performance is worse than the first method. The conclusion is also verified by actual measurements from the in-orbit CubeSats.

Keywords:CubeSat; two-line element; SGP4 model; Doppler shift

收稿日期：2015-03-03；修回日期：2015-10-23；网络优先出版日期：2016-01-12。

基金项目：欧盟第七科研框架计划QB50项目(284427)；教育部科技发展中心博士点基金(20133219120030)；江苏省高校优势学科建设项目资助课题

中图分类号：V 448.232

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.22

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160112.1741.012.html