基于线性变换的阵列幅相误差自校正算法

曲志昱, 吴　迪, 王　炎

(1.哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001;2.中航工业雷达所北京创新中心, 北京 100012)



基于线性变换的阵列幅相误差自校正算法

曲志昱1, 吴迪2, 王炎1

(1.哈尔滨工程大学信息与通信工程学院, 黑龙江 哈尔滨 150001;2.中航工业雷达所北京创新中心, 北京 100012)

摘要：针对天线阵列的幅相误差严重影响阵列测向算法估计性能的问题,提出了一种基于线性变换的阵列幅相误差自校正算法。该方法通过利用幅度相位特性一致的辅助阵元,进行矩阵的正交线性变换,并结合最小二乘法算法,有效地估计阵列的幅相误差系数和入射信号的波达方向。其不需要谱峰搜索,无特征分解运算,计算量小,复杂度低,可实现对阵列幅相误差的快速校正。计算机仿真实验结果验证了该算法估计性能的有效性。

关键词：波达方向估计; 阵列幅相误差; 自校正; 线性变换

0引言

辐射信号的波达方向(direction of arrival,DOA)估计[1-3]一直是信号处理领域的重要研究内容,其在通信、雷达、侦查、探测和定位等许多领域有着广泛的应用,从而受到了国内外专家学者广泛的关注[4-5]。相继出现了众多经典算法,包括多重信号分类(multiple signal classification, MUSIC)算法[4]和旋转不变子空间(estimation of signal parameters via rotational invariance techniques, ESPRIT)算法[5]等。然而其良好的测向性能是建立在精确已知阵列流形的基础上的。但是在实际被动阵列测向系统中,各天线阵元的电磁特性不一致,位置偏差等因素不可避免。这些因素产生的结果都会转化为接收数据中存在的幅相误差。这时阵列测向算法的测向性能将急剧下降[6-7]。从而就需要研究在阵列误差条件下的DOA估计方法。该方法一般通过对阵列幅相误差的有效校正来实现。

近年来,涌现出了大量的研究算法,大体上包括有源校正[8-9],循环优化迭代自校正[10-16]以及矩阵变换类的自校正[17-22]等研究方向。有源校正类算法是要在空间设置方位精确已知的辅助信源。文献[8]利用一系列位置已知的信号源来求解包含多种误差参数的校正矩阵,从而对阵列误差进行校正。文献[9]采用单个连续波校正源,通过旋转阵列天线,完成单个辅助源的校正。有源校正需要外置辅助源或其他辅助设施,增加了测向设备的成本,对硬件和环境的要求严格,在很多情况下并不适用。

针对不同的阵列结构和误差模型,循环优化迭代类自校正技术已得到深入的研究。文献[10-11]基于子空间正交原理提出将阵列误差参数与方向参数同时进行迭代估计的WF自校正算法,为此类校正技术最为典型的代表。文献[12]对WF自校正算法中的相位迭代校正做了全面的分析,指出此校正技术会出现相位模糊的现象。文献[13]能够同时估计信号DOA和阵列误差参数,但是其以阵列扰动误差较小为前提,同时全局最优解无法保证。除了迭代估计算法,还有一种基于最大似然或子空间拟合原理的多维参数估计类自校正技术[14-16]。但是这类算法都需要求解非线性的多维最优化问题,利用全局极值的多维搜索,计算量较大。

为了克服此类问题,学者们正在积极研究基于矩阵变换的自校正技术。此类方法不需要多维循环迭代以及设置初值,可以直接估计出入射信号的DOA以及阵列误差参数。文献[17]中,提出一种可工程实现的DOA估计方法,其利用了阵列接收数据和其共轭的点积。文献[18]对这种方法进行了改进,但是这两种方法都只有在空间中存在至少两个信号时才能应用。另外,学者们也在研究使用部分阵元或者利用辅助阵元,使阵列误差矩阵构成某种特殊结构,来实现在幅相误差下的DOA估计。一类非常著名的算法是利用秩损估计(rank reduction estimation, RARE)器[2, 19-21],但是其需要谱峰搜索过程。文献[22]提出了一种简单、有效的基于传统ESPRIT算法的部分阵列DOA估计方法,但是涉及矩阵的特征分解运算,同时估计精度有待提高。

本文针对阵列幅相误差问题,提出一种校正方法,实现对阵列幅相误差系数和辐射信号DOA的正确估计。其基于正交线性变换思想[23],利用幅度相位性能一致的辅助阵元,进行矩阵变换,并与最小二乘法相结合,首先估计出阵列幅相误差系数,然后估计出空间中入射信号的DOA。希望通过对该方法的研究,推动阵列测向方法在实际系统中的应用。

1数学模型

设天线阵列是间距为d的M个天线阵元组成的均匀线阵。N个窄带远场独立的辐射信号s1(t),s2(t),…,sN(t)从方向θ1,θ2,…,θN入射。噪声服从高斯分布,均值为零,方差为σ2,信号与噪声之间相互独立。接收到的数据可表示为

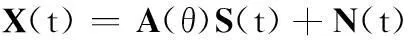
(1)

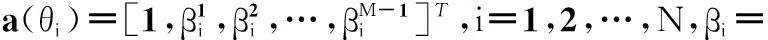
R=ARSAH+σ2I

(2)

式中,RS=E[S(t)S(t)H]为信号的协方差矩阵;I为单位矩阵;σ2为噪声功率。

这里用ρ1,…,ρM和φ1,…,φM来表征阵列接收数据的幅度和相位误差系数。那么可定义M×1维的幅相误差矢量

(3)

M×M维的幅相误差矩阵

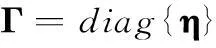
(4)

阵列幅相误差下的阵列流形可以表示为

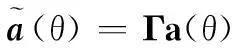
(5)

接收数据受到幅相误差的影响

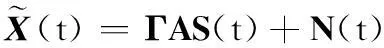
(6)

(7)

这样就需要研究在阵列幅相误差模型下,对辐射信号DOA的估计方法。

2算法原理

设M个阵元中有q个阵元的幅相误差精确校准,将此q个阵元称为辅助阵元。把均匀线阵分成两个子阵,其中前M-1个阵元构成子阵1,后M-1个阵元构成子阵2,则两个子阵的导向矢量可分别表示为

(8)

(9)

式中,(M-1)×N维矩阵A1和A2分别表示两个子阵的理想导向矢量;Γ1和Γ2分别表示两个子阵的幅相误差矩阵,可以写为

(10)

(11)

A1和A2满足

(12)

式中,Φ=diag{ej2πdsin θ1/λ,ej2πdsin θ2/λ,…,ej2πdsin θN/λ}。

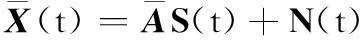
(13)

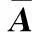
(14)

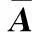
(15)

式中,B1和B2分别为N×N维和(2(M-1)-n)×N维矩阵。B1的N行元素线性独立,B2可由B1的线性变换表示,即

PHB1=B2

(16)

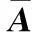
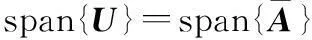
(17)

此时就存在一个唯一的N×N非奇异矩阵T,满足

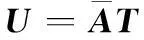
(18)

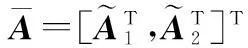
(19)

式中,N×(M-1-n)维P1、N×N维P2和N×(M-1-n)维P3为P的3个子阵,即

(20)

那么,此时可以得到

(21)

可推导出

(22)

式中,Ψ=T-1ΦT,为N×N维Φ的相似矩阵。则Ψ的特征值是Φ的对角线元素,Ψ的特征向量为矩阵T的各列。

那么只要估计出矩阵Ψ,对其进行特征分解,即可得到它的N个特征值e1,e1…,eN,从而就可以估计出入射信号的DOA为

(23)

而对于式(22),又可进一步化简为

(24)

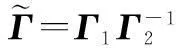
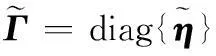
(25)

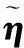
(26)

根据式(26)中的定义,可以很容易推得幅相误差系数的求解表达式,即

(27)

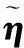
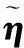
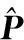
(28)

先对协方差矩阵去噪,然后再估计传播算子,令

(29)

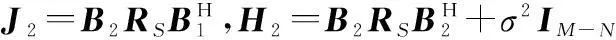
(30)

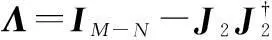
(31)

(32)

式中,G为2(M-1)×N维矩阵;H为2(M-1)×(2(M-1)-N)维矩阵,且二者满足关系

H=GP

(33)

(34)

式中,‖·‖F表示Frobenius范数。

通过求解可以得到

(35)

(36)

以Ψ为变量,最小化上式给出的目标函数,可以得到Ψ的如下最小二乘解

(37)

(38)

(39)

再将式(25)代入式(39),能够推得

(40)

其中⊙表示Hadamard积。令

(41)

那么根据式(39)、式(40)和式(41)的推导,可得

(42)

(43)

这样,求解式(36)目标函数最小化的问题就转化为了线性约束下的优化问题,即

(44)

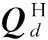
(45)

令

(46)

从而得到方程组

(47)

将此方程组写成矩阵形式

(48)

通过推导,可以求解出

(49)

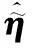
求出阵列幅相误差系数后,可以进一步得到阵列幅相误差矩阵,即

(50)

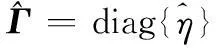
(51)

利用估计出的阵列幅相误差矩阵,就可以进一步校正阵列流形,达到幅相误差校正的目的。

目前对于基于辅助阵元的幅度相位校正类方法的研究非常广泛,其中典型的算法就包括文献[21]中的RARE算法和文献[22]给出的基于ESPRIT的幅相误差校正算法。RARE算法在实现过程中,需要矩阵特征分解运算和谱峰搜索过程,这将带来巨大的运算量,增加了算法的复杂度。文献[22]方法接近传统的ESPRIT算法,不需要进行谱峰搜索,但是其需要特征分解运算。

这里单独考虑求解子空间方法的复数计算量,设采样数据快拍数为1。如使用特征分解法求解子空间,求解协方差矩阵的计算量为O(M2),需要对协方差矩阵再进行特征分解运算,特征分解运算的计算量共为O(M2+M3)。而对于本文基于正交线性变换思想的子空间求解方法,根据式(35),其对应的复数计算量为O(N2+N3+N(M-N)+(M-N)2)[24]。由于要保证无模糊测向,信源数N必然小于阵元数M,而且本文方法无三次方的复乘运算,所以本文方法的计算量要小于文献[22]方法。各方法复数乘法运算复杂度对比如表1所示。

表1　运算复杂度对比

3实验分析

下面通过仿真实验验证本文方法在估计辐射信号DOA和阵列幅相误差系数方面的性能。并与同样利用辅助阵元进行幅相误差校正的RARE方法[21]和文献[22]方法的进行性能对比。

实验条件:采用9阵元均匀线阵,阵元间距为入射信号的半波长。2个非相干入射信号角度为-10°和10°。前4个阵元为幅度相位特性一致的辅助阵元,其余5个阵元的幅相误差向量η=[0.6ejπ/6,0.8e-jπ/18,1.53e-jπ/15,0.75ejπ/20,1.36e-jπ/10]T。噪声为零均值高斯白噪声。统计实验时,蒙特卡罗实验次数为100次。

实验中,DOA估计的均方根误差定义为

(52)

幅度和相位误差系数估计的均方根误差定义为

(53)

(54)

分辨成功概率定义为正确分辨的次数与实验次数的比值,其中估计的角度误差小于真实角度间隔的一半时认为正确分辨。

实验 1测角精度。实验中设置了4个无幅相误差的辅助阵元,可以使用经典空间谱估计算法,进行DOA估计。这里将本文方法的DOA估计性能与只利用4个无幅相误差阵元的MUSIC算法,ESPRIT算法和PM算法的估计性能进行比较。快拍数为100,不同信噪比下各个算法DOA估计的均方根误差如图1所示;信噪比为10dB,不同快拍数下各个算法DOA估计的均方根误差如图2所示。比较本文方法,RARE算法和文献[22]算法的DOA估计性能。快拍数为100,不同信噪比下各个算法DOA估计的均方根误差如图3所示;信噪比为10dB,不同快拍数下各个算法DOA估计的均方根误差如图4所示。

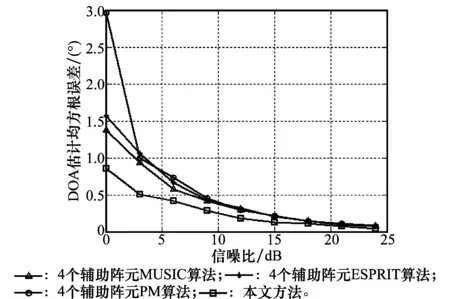
图1　信噪比对DOA估计均方根误差的影响

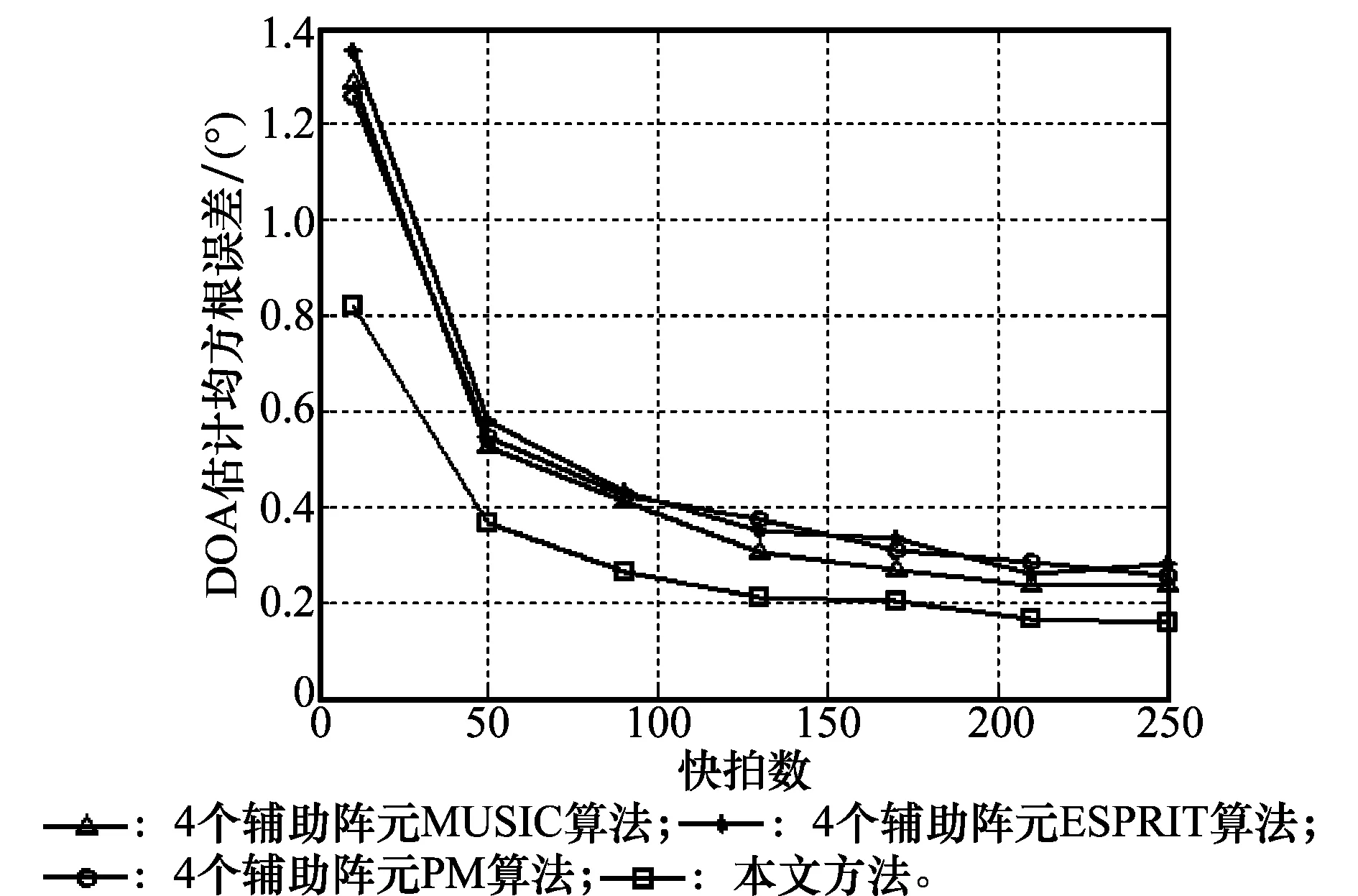
图2　快拍数对DOA估计均方根误差的影响

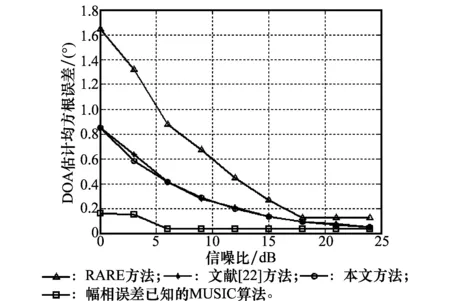
图3　信噪比对DOA估计均方根误差的影响

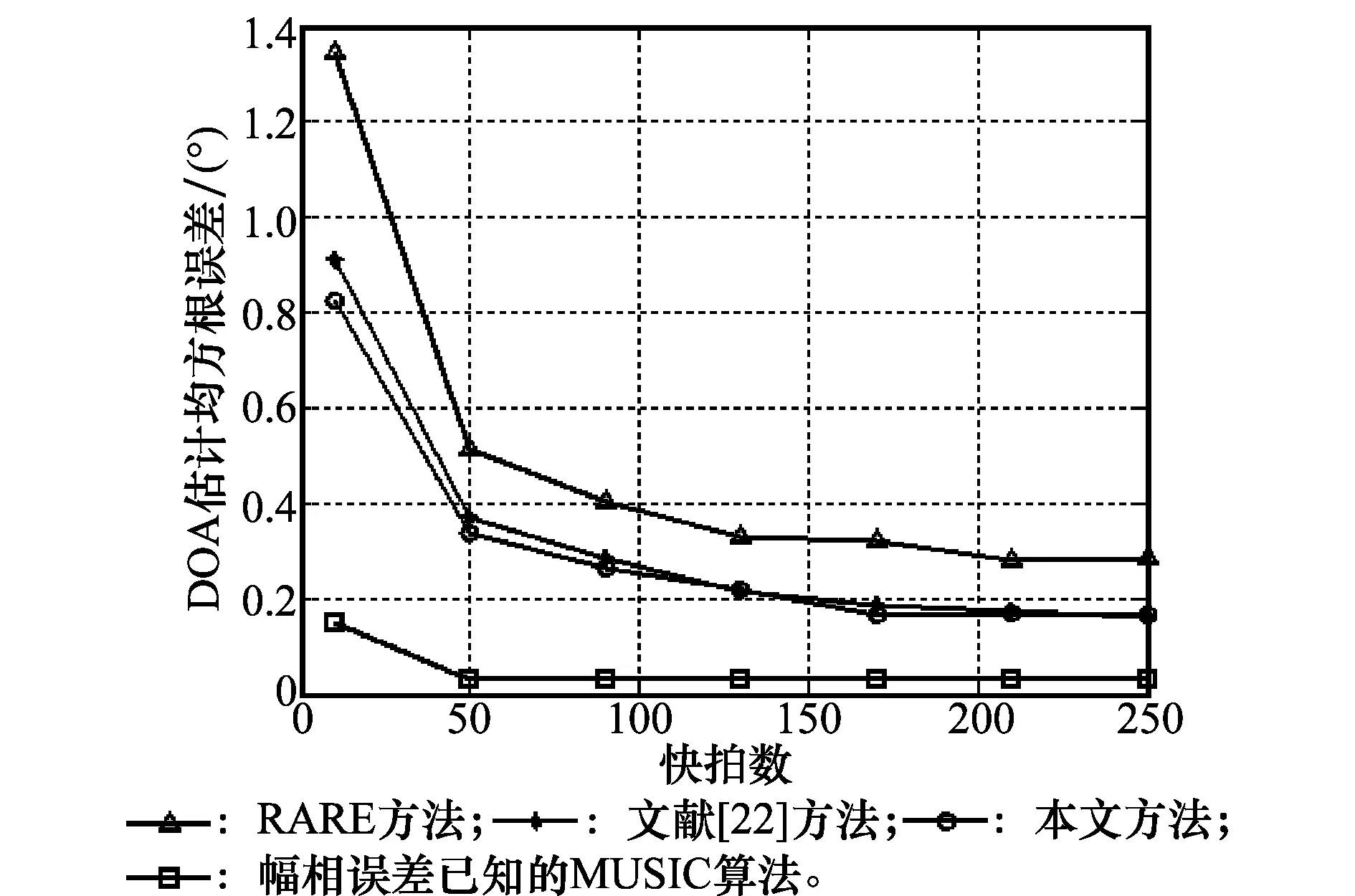
图4　快拍数对DOA估计均方根误差的影响

仿真结果表明,本文方法的DOA估计精度比只用4个辅助阵元的空间谱估计方法高。这是因为本文方法利用了较多阵元的接收数据,虽然其余五个阵元具有幅相误差,但是本文方法做了有效的校正。同时,与其他同样进行了幅相误差校正的方法相比,本文方法同样具有较高的DOA估计精度。

实验 2分辨概率。对比本文校正方法,RARE方法和文献[22]方法对多个信号分辨成功概率的统计结果。对不同信噪比和不同快拍数条件下的分辨成功概率进行统计,取快拍数100,信噪比10dB,仿真统计结果如图5和图6所示。

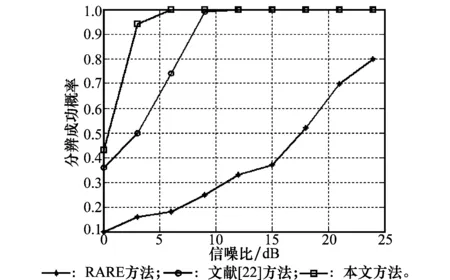
图5　信噪比对成功分辨概率的影响

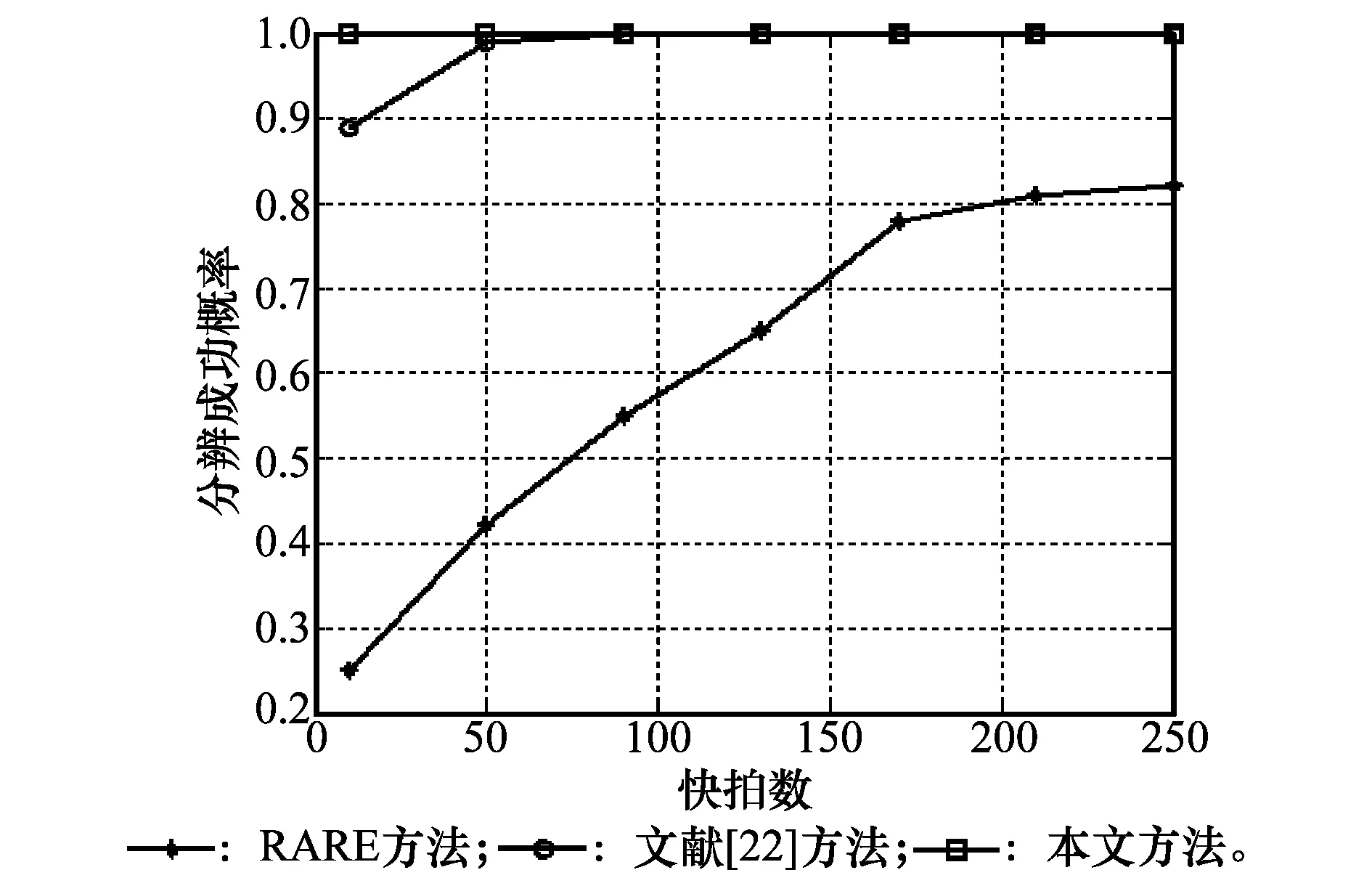
图6　快拍数对成功分辨概率的影响

由图5和图6可以看出,在一定的信噪比和快拍数门限内,3种方法对2个信号的分辨成功概率均随信噪比的增加而增大,随快拍数的增多而提高。当信噪比高于10dB,快拍数高于50时,本文方法和文献[22]方法的分辨成功概率可以达到100%,3种方法中,本文方法的分辨性能最高,其次为文献[22]方法,再次为RARE方法。

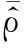
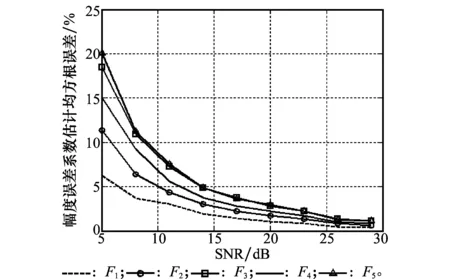
图7　幅度误差估计的均方根误差

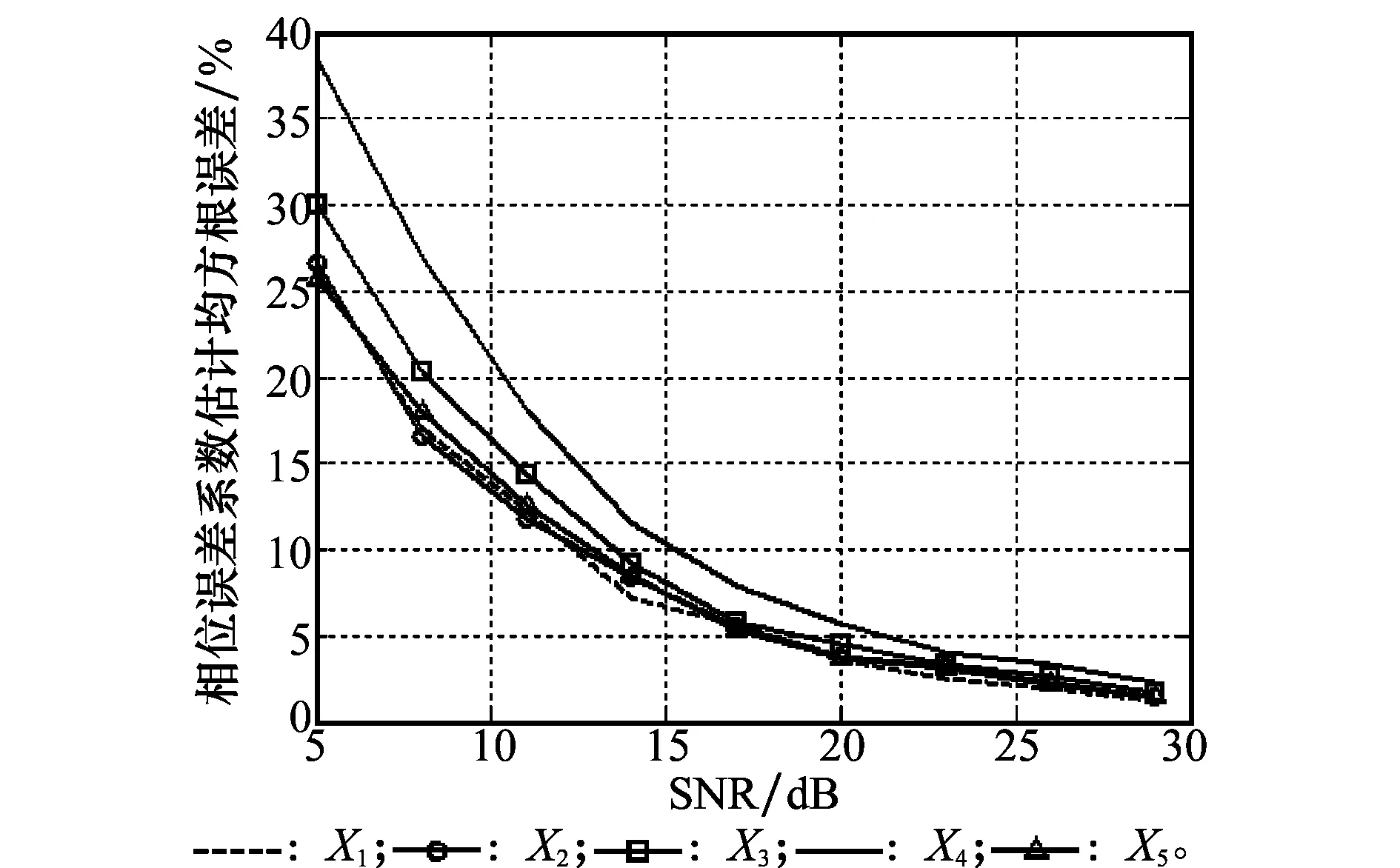
图8　相位误差估计的均方根误差

仿真结果表明,本文方法对幅相误差系数的估计精度随着信噪比的增加而提高。当信噪比高于15dB,本文方法对幅相误差估计的均方根误差低于10%。从而可以说明,当信噪比足够高时,本文方法对幅度和相位误差的估计可以达到较高的估计精度和稳定性。

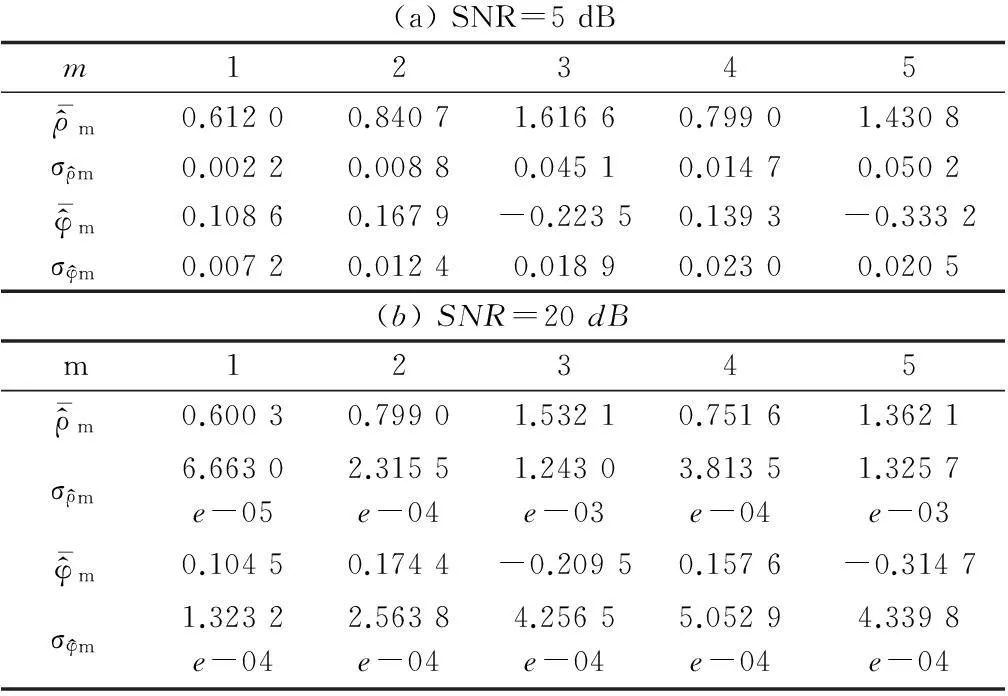
表2　幅度和相位误差估计的均值和方差

4结论

实际被动阵列测向系统中,阵列幅相误差严重影响测向算法性能。本文提出一种基于线性变换的阵列幅相误差自校正算法,能够有效地估计出阵列幅相误差系数和辐射信号的DOA。与其他相关方法相比,其不需要谱峰搜索,无特征分解运算,算法计算量小,复杂度低。仿真结果表明,该方法能够获得较高的DOA估计性能和幅相误差系数的估计精度。通过本文方法的研究,可以进一步推动阵列测向方法在实际被动测向系统中的应用。

参考文献：

[1] Reddy V V, Mubeen M, Ng B P. Reduced-complexity super-resolution DOA estimation with unknown number of sources[J].IEEESignalProcessingLetters, 2015, 22(6): 772-776.

[2] Dai J, Bao X, Hu N, et al. A recursive RARE algorithm for DOA estimation with unknown mutual coupling[J].IEEEAntennasandWirelessPropagationLetters,2014,13(5):1593-1596.

[3] Wang L M, Chen Z H, Wang G B, et al. Underdetermined DOA estimation and blind separation of non-disjoint sources in time-frequency domain based on sparse representation method[J].JournalofSystemsEngineeringandElectronics, 2015, 26(1): 44-49.

[4] Schmidt R O. Multiple emitter location and signal parameter estimation[J].IEEETrans.onAntennasandPropagation, 1986, 34(3): 276-280.

[5] Roy R, Paulraj A, Kailath T. ESPRIT—a subspace rotation approach to estimation of parameters of cisoids in noise[J].IEEETrans.onAcoustics,SpeechandSignalProcessing,1986,34(5):1340-1342.

[6] Yuan Z Y, Niu Y M, Yang G, et al. A calibration method for sensor gain/phase and position errors of array antenna[J].JournalofElectronics&InformationTechnology, 2014, 36(9): 2232-2237.(袁自月,牛一鸣,杨国,等.一种阵列天线阵元幅相、位置误差校正方法[J].电子与信息学报,2014,36(9):2232-2237.

[7] Ferreol A, Larzabal P, Viberg M. On the resolution probability of music in presence of modeling errors[J].IEEETrans.onSignalProcessing, 2008, 56(5): 1945-1953.

[8] Ng B C, See C M S. Sensor-array calibration using a maximum-likelihood approach[J].IEEETrans.onAntennasandPropagation, 1996, 44(6): 827-835.

[9] Wang D, Wu Y. Improved active array calibration algorithm for mutual coupling and amplitude-phase error of uniform linear array[J].SystemsEngineeringandElectronics,2009,31(9):2076-2081.(王鼎,吴瑛.均匀线阵互耦和幅相误差有源校正改进算法[J].系统工程与电子技术,2009,31(9):2076-2081.)

[10] Friedlander B, Weiss A J. Direction finding in the presence of mutual coupling[J].IEEETrans.onAntennasandPropagation, 1991, 39(3): 273-284.

[11] Weiss A J, Friedlander B. Array shape calibration using eigenstructure methods[J].SignalProcessing, 1991,22(3): 251-258.

[12] Hung E K L. A critical study of a self-calibration direction-finding method for array[J].IEEETrans.onSignalProcessing,1994,42(2):471-474.

[13] Soon V C, Tong L, Huang Y F, et al. A subspace method for estimating sensor gains and phases[J].IEEETrans.onSignalProcessing, 1994, 42(4): 973-976.

[14] Viberg M, Swindlehurst A L. A Bayesian approach to auto-calibration for parametric array signal processing[J].IEEETrans.onSignalProcessing, 1994, 42(12): 3495-3507.

[15] Wang D, Yao H, Wu Y. The joint calibration algorithms of mutual coupling and gain-and-phase errors based on covariance matching technique[J].ActaElectronicaSinica,2012,40(3):580-586.(王鼎,姚晖,吴瑛.基于协方差匹配技术的互耦和幅相误差联合校正算法[J].电子学报,2012,40(3):580-586.)

[16] Sellone F, Serra A. A novel online mutual coupling compensation algorithm for uniform and linear arrays[J].IEEETrans.onSignalProcessing, 2007, 55(2): 560-573.

[17] Liu A, Liao G, Zeng C, et al. An eigenstructure method for estimating DOA and sensor gain-phase errors[J].IEEETrans.onSignalProcessing, 2011,59(12) 5944-5956.

[18] Cao S, Ye Z, Xu D, et al. A hadamard product based method for DOA estimation and gain-phase error calibration[J].IEEETrans.onAerospaceandElectronicSystems,2013，49(2):1224-1233.

[19] Pesavento M, Gershman A B, Wong K M. Direction finding in partly-calibrated sensor arrays composed of multiple subarrays[J].IEEETrans.onSignalProcessing, 2002, 50(9): 2103-2115.

[20] See C M, Gershman A B. Direction-of-arrival estimation in partly calibrated subarray-based sensor arrays[J].IEEETrans.onSignalProcessing, 2004, 52(2): 329-338.

[21] Elkader S A, Gershman A B, Wong K M. Rank reduction direction-of-arrival estimators with an improved robustness against subarray orientation errors[J].IEEETrans.onSignalProcessing, 2006, 54(5): 1951-1955.

[22] Liao B, Chan S C. Direction finding with partly calibrated uniform linear arrays[J].IEEETrans.onAntennasandPropagation, 2012, 60(2): 922-929.

[23] Wang F Q, Zhang X F. Improved propagator method-based joint TOA and DOA Estimation in impulse radio ultra wide band[J].JournalofElectronics&InformationTechnology, 2013, 35(12): 2954-2959. (王方秋, 张小飞. 脉冲超宽带系统中基于改进传播算子算法的 TOA 和 DOA 联合估计[J].电子与信息学报, 2013, 35(12): 2954-2959.)

[24] Liu L T. The research on key technique of direction of arrival for passive detection system[D].Harbin：Harbin Engineering University, 2011. (刘鲁涛.无源探测系统DOA关键技术研究[D].哈尔滨:哈尔滨工程大学,2011.)

曲志昱(1983-),女,副教授,博士,主要研究方向为宽带信号检测、处理与识别及高分辨高精度测向技术。

E-mail:quzhiyu@hrbeu.edu.cn

吴迪(1987-),女,博士研究生,主要研究方向为高分辨高精度测向技术、阵列误差校正技术。

E-mail:wudi7212@126.com

王炎(1992-)，男,博士研究生,主要研究方向为高分辨高精度测向技术。

E-mail:wangyan17855@163.com

Self-calibration method of gain/phase error based on linear transformation

QU Zhi-Yu1, WU Di2, WANG Yan1

(1.CollegeofInformationandCommunicationEngineering,HarbinEngineeringUniversity,Harbin150001,China;2.RadarResearch(Beijing)LeihuaElectronicTechnologyInstitute,Beijing100012,China)

Abstract:Processing the signals received on an array of sensors for localization of multiple emitters is of great interest. However, the common array gain/phase errors will severely affect the estimation performance of direction finding algorithms. In this paper, a self-calibration method of gain/phase errors based on linear transformation is proposed. Both the gain/phase coefficients and direction of arrival (DOA) can be estimated effectively by a sequence of processes including applying a group of instrumental sensors with consistent gain/phase performance, converting and deriving the matrix by using the orthogonal linear transformation as well as combining the least squares method. The proposed algorithm is able to self-calibrate the array gain/phase errors without spectral searching and matrix decomposition, there it is low in computational load and complexity. Furthermore, the computer simulation results verify the effectiveness and superiority of the algorithm.

Keywords:direction of arrival (DOA) estimation; array gain/phase errors; self-calibration; linear transformation

收稿日期：2015-05-28；修回日期：2015-10-18；网络优先出版日期：2016-01-27。

基金项目：航空科学基金(201401P6001)；中央高校基本科研业务费重点专项资金项目(HEUCF150804)资助课题

中图分类号：TN 911

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.02

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160127.1541.008.html