岸海空协同探测目标高度补偿估计技术

司记伟, 田燕妮, 潘莉莉, 刘思琦

(1. 海军航空工程学院科研部, 山东 烟台 264001; 2. 中国人民解放军92857部队, 北京 100161;3. 张家口职业技术学院电气工程系, 河北 张家口 075000)



岸海空协同探测目标高度补偿估计技术

司记伟1, 田燕妮2, 潘莉莉1, 刘思琦3

(1. 海军航空工程学院科研部, 山东 烟台 264001; 2. 中国人民解放军92857部队, 北京 100161;3. 张家口职业技术学院电气工程系, 河北 张家口 075000)

摘要：针对现有高度估计算法缺乏对实际多雷达组网系统信息处理流程的考虑致使算法难以在实际系统中运用的问题,在岸海空协同预警体系下,从信息处理流程和信息处理方法两个方面,在探测单元信息缺维情况下,研究目标高度补偿问题。仿真结果表明,本文给出的算法可实现目标状态的无偏、稳定、精确估计,最终得到的目标海拔高度补偿估计结果可满足目标属性判别和威胁判断的需要。另外仿真验证表明,本文算法对目标巡航高度具有很强的适应性,可用于解决处于岸海空探测单元共视范围内任意高度飞行目标的高度补偿问题。

关键词：协同预警; 高度补偿; 伪量测; 扩展卡尔曼滤波

0引言

岸海空协同探测系统通过对岸基、舰载和机载探测单元进行组网融合,可有效结合位于不同方位、不同高度的探测单元对目标的探测优势,实现战场区域的多节点、多角度、大范围覆盖探测,并可有效对抗隐身突防、巡航弹饱和攻击、电磁掩护突防以及反辐射攻击等单一类传感器难以应对的空袭方式,从而确保我国濒海重点区域的安全[1-2]。

岸海空协同探测系统通过对来自多种探测单元的信息依次进行位置、属性、态势以及威胁等融合估计,来实现目标属性判别、重点目标选取以及火控质量级目标状态估计,并最终据此来有效完成防空拦截反击的作战任务。然而不同探测单元间的信息维度是不一致的,难以进行直接的融合处理,并且大多数探测单元的信息维度较低,无法满足空间定位的需要,迫切需要通过协同组网实现信息的补偿。结合实际装备情况,本文重点对协同组网高度补偿技术进行研究。

目标高度补偿技术是岸海空协同探测系统的关键技术,国内外学者在该领域进行了有益的探索,并取得了一批有用的研究成果。根据雷达以及目标之间空间几何关系不同,文献[3-7]利用多部雷达对目标的距离方位同时进行量测,并结合雷达所处的空间位置,得到一定条件下对目标高度的估计。若假设目标高度不变,此时还可求得量测高度的时间累计估计。文献[8-12]研究了匀速等高运动的目标在直角坐标系中,以目标高度作为参量,利用多部雷达对同一目标的距离方位量测,采用多假设滤波方法,补偿估计目标高度。通过对上述算法深入分析发现,它们对自身在信息处理流程中的位置并没有作特别考虑,然而实际上由于需要对多部探测单元的量测进行处理,算法仅能在协同中心运行。并且上述算法是利用各探测单元的原始量测来实现目标高度补偿估计的,然而实际上由于系统通信能力和处理能力有限,岸基、舰载和机载探测单元仅能向协同中心上传经过滤波处理之后的重点目标航迹信息。

如上所述,随着对目标高度补偿估计技术研究的不断深入,国内外已有不少学者在该领域取得了一些成果,但由于缺乏对实际系统架构和流程的考虑,现有算法在实际工程应用中仍存在诸多的问题[13-24]。针对这些问题,本文在我岸海空协同预警体系下,从信息处理流程和信息处理方法两个方面,对探测单元信息缺维情况下的目标高度补偿算法展开研究。

1系统模型

本文所研究算法针对的典型战场环境为:一个或多个敌方目标正向我方要地逼近,我方岸基雷达、机载雷达和舰载雷达都已稳定跟踪到目标,并利用通信链路把目标的航迹数据上传到岸海空协同探测中心;在协同中心对不同探测单元的目标数据进行航迹关联、维度补偿、航迹融合、属性判别以及威胁判断,如果目标威胁达到一定的等级,则往火力单元装订目标数据,发射导弹进行拦截。在岸海空协同探测系统的整个信息处理流程中,本文主要对其中的目标高度补偿技术进行研究。

假设岸基雷达、舰载雷达和机载雷达均为两坐标雷达,仅能得到目标的距离和方位量测。根据岸海空协同探测系统的特点,本文设计如下的信息处理流程:岸基、舰载和机载雷达首先分别各自在协同中心FT坐标系中对目标进行缺维有偏跟踪,并把跟踪结果上传到协同中心,然后协同中心通过对多部雷达的航迹进行融合估计,来实现目标的高度补偿估计。本节主要对系统模型以及各探测单元上的处理算法进行研究,下一节主要对协同中心上的处理算法进行研究。

为了便于后边的表述,下面首先明确几种坐标系。

地球地理(latitude-longitude-altitude,LLA)坐标系:利用纬度、经度、高度表示目标在地球参考系上的位置,本文采用WGS-84地球参考系。

地球直角(central body fixed,CBF)坐标系:坐标系原点位于地心处,X轴指向0°经线,Y轴指向90°经线,Z轴指向北极点,满足右手定律。

地球表面(fusion topocentric,FT)坐标系:以地球表面某一点为坐标原点,X轴指向南,Y轴指向东,按照右手定律,Z轴的指向为沿垂直地球表面的方向沿法线方向指向高空,协同中心即采用该类型坐标系。

本地水平(local horizontal,LH)坐标系:固定平台的量测坐标系,以地球表面平台中心点为坐标原点,X轴指向北,Y轴指向东,Z轴沿表面法线指向地心,满足右手定律,岸基雷达即在该坐标系下对目标进行量测。

平台速度本地水平(vehicle velocity local horizontal,VVLH)坐标系:机动平台的量测坐标系,以平台中心点为坐标原点,Z轴指向平台位置矢量(CBF坐标系)的反方向,Y轴指向Z轴与速度矢量所构平面的法向量,X轴指向Y轴与Z轴所构平面的法向量,满足右手定律,机载、舰载雷达即在该坐标系下对目标进行量测。

根据实际运动中目标的运动特点,按照预先设定的航线(等角航线或大圆航线),可使目标按照预先设定的航线在CBF坐标系中按照匀速巡航模式运动。由于FT坐标系可看做是CBF坐标系经过线性变换(旋转和平移等)得到的,因而在FT坐标系中,可将目标的运动认为是匀速直线运动。

1.1目标状态方程

定义k时刻目标在FT坐标系中的状态为x(k)=[x(k) vx(k)y(k)vy(k)z(k)vz(k)]′,根据上面关于目标运动的假设,可得目标的状态转移方程为

(1)

其中，状态转移矩阵F定义为

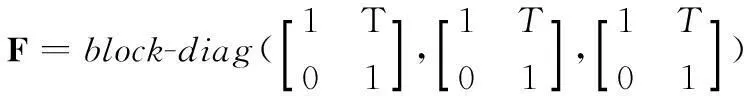
(2)

式中,block-diag(·)表示块对角阵;T是离散化的采样间隔;v(k)表示目标状态方程中的过程噪声,为零均值白色高斯过程噪声,其中v(k)的协方差表示如式(3)～式(6)所示,其大小可根据目标实际航迹与系统假定航迹间的偏离程度来设定。

Q=block-diag(Qx,Qy,Qz)

(3)

(4)

(5)

(6)

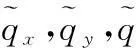
1.2岸海空探测单元的量测方程

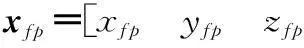
(7)

式中，xct(k)为目标在CBF坐标系中的坐标；TFTC(Lfp)为FT坐标系到CBF坐标系的旋转矩阵,其大小为

(8)

H为常量矩阵,其大小为

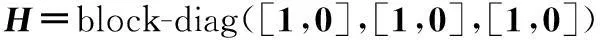
(9)

(10)

式中，xlt(k)为目标在岸基雷达LH坐标系中的坐标;TCTL(Lfp)为CBF坐标系到LH坐标系的旋转矩阵,其大小为

(11)

岸基雷达对目标距离方位的量测是在LH坐标系中进行的,量测存在一定的噪声,其方程为

(12)

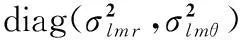
(13)

同时,联合式(7)和式(10),可得

(14)

将式(14)代入到式(12),可得岸基雷达的量测方程为

(15)

设在k时刻,预警机在CBF坐标系中的位置为xap(k)=[xap(k)yap(k)zap(k)]′,速度为vap(k)=[vxap(k)vyap(k)vzap(k)]′。根据CBF坐标系与VVLH坐标系之间的转换关系,可由目标在CBF坐标系中的坐标xct(k)得到目标在机载雷达VVLH量测坐标系中的坐标

(16)

式中，xat(k)为目标在机载雷达VVLH坐标系中的坐标；TCTV(g(xap),g(vap))为CBF坐标系到VVLH坐标系的旋转矩阵,g(xap)为向量归一化函数,它们的表达式为

(17)

(18)

机载雷达对目标距离方位的量测是在VVLH坐标系中进行的,量测过程中存在一定的噪声,其方程为

(19)

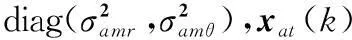
(20)

将式(20)代入到式(19),可得机载雷达的量测方程为

(21)

设在k时刻,舰艇在CBF坐标系中的位置为xsp(k)=[xsp(k)ysp(k)zsp(k)]′,速度为vsp(k)=[vxsp(k)vysp(k)vzsp(k)]′。根据式(16),可把目标在CBF坐标系中的位置坐标xct(k)转换到舰载雷达的VVLH量测坐标系中,得到xst(k),继而可得舰载雷达的量测方程为

(22)

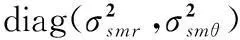
从雷达的距离方位缺维原始量测到目标在FT坐标系中的坐标,涉及多个坐标系之间的变换,在量测极坐标系中一个维度的完全缺失,变换到FT坐标系中将会表现为所有维度的部分可观测(有的维度可能表现为基本不可观测),即导致FT坐标系中的坐标存在一定的偏差。以岸基雷达量测为例,其转换到FT坐标系中,是可以得到X/Y/Z轴的坐标分量的,但由于俯仰角信息的缺失,导致其在FT坐标系中的坐标与真实坐标存在一定的偏差(Z轴方向偏差较大),难以对目标进行精确定位。通过上面的分析可知,原始量测的缺维将会导致FT的坐标有偏,本文所说的缺维有偏跟踪指的是在原始量测缺维引起FT坐标有偏情况下的目标跟踪过程。

岸海空探测单元采用扩展卡尔曼滤波算法在FT坐标系中对目标进行跟踪。目标的状态方程如式(1)所示,岸海空单元的量测方程如式(12)、式(22)和式(21)所示。采用泰勒级数对量测方程进行线性展开,其中函数h(x)(见式(13))关于向量x(仅表示变量)的雅可比矩阵为

(23)

根据复合函数的求导公式,联合式(15)和式(14),可得岸基雷达量测方程h(U(x(k)))关于目标状态x(k)的雅可比矩阵为

(24)

同理，可分别得机载雷达量测方程h(V(x(k),xap(k),vap(k)))、舰载雷达量测方程h(V(x(k),xsp(k),vsp(k)))关于目标状态x(k)的雅可比矩阵为

(25)

(26)

由于岸海空探测单元具有相似的目标状态转移方程和雷达量测方程,因而它们的滤波方程组也是相似的,下面仅以岸基雷达为例对其滤波过程进行详细说明[12-17]。

利用已求得的雅可比矩阵,结合扩展卡尔曼滤波方程组,可得岸基雷达对目标的有偏跟踪方程组为

(27)

(28)

(29)

(30)

(31)

(32)

2目标高度补偿估计

由目标状态的可观测性分析可知,单个探测单元是难以实现目标高度补偿估计的,必须有效结合多个探测单元在不同方向对目标状态的观测,才能实现目标的高度补偿估计。因而岸海空协同探测系统仅能在协同中心利用不同探测单元对目标的有偏跟踪结果来实现目标的高度补偿估计。

下面首先利用探测单元上传的目标跟踪结果,通过可逆运算获取探测单元对目标的距离方位伪量测,据此构建岸海空探测单元联合量测方程,然后使用扩展卡尔曼方程组对目标状态进行估计,可得到目标的无偏状态估计,从而最终实现目标高度的补偿估计。

小虫呼呼睡了，玉敏没睡着，玉敏想了许多。她把这事前前后后反复地想了，竟生了若干感悟。玉敏最大的感悟，是在每个人的心里，其实都藏着一个魔。这个魔法力无边，驱使着每个人去做一些不道德甚至违心的事。如果不是这个魔，又怎么会上演这幕闹剧呢？

2.1探测单元伪量测

结论 1平台的滤波增益K(k+1)为列满秩矩阵。

下面以岸基探测平台的滤波增益Kl(k+1)为例进行证明,机载、舰载平台的证明方法相同。

由式(28)、式(29)可知,Pl(k+1|k),Sl(k+1)为正定矩阵,是可逆的。

在式(23)中,H0(x)的一个2阶行列子式为

(33)

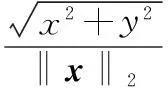
对矩阵H进行如下初等列变换

(34)

式中，C为初等变换矩阵

(35)

代入式(34)到式(24),可得

(36)

由于TCTL(Llp),TFTC(Lfp),I3×3均为单位可逆矩阵,因而rank(H0(x))=rank(H0(U(x))TCTL(Llp)TFTC(Lfp)I3×3)=2。又由于C为初等变换矩阵,Hl(x)为2×6矩阵,因此rank(Hl(x))=2,Hl(x)为行满秩矩阵。

由于一个矩阵和一个可逆矩阵相乘,其矩阵秩不变,结合式(30),可知Kl(k+1)为6×2矩阵,其矩阵秩rank(Kl(k+1))=2,为列满秩矩阵。

结论 2K的唯一加号逆为K+=(KTK)-1KT。

由于K为列满秩矩阵,KTK为可逆方阵,是可逆的,下面验证(KTK)1KT是否满足矩阵加号逆的定件。

KK+K=K(KTK)-1KTK=K

(37)

(38)

(39)

(40)

因此，(KTK)-1KT为K的加号逆。

下面证明K的加号逆是唯一的。设X,Y均为K的加号逆,于是同时有

KXK=K, KYK=K

(41)

用Y右乘上面的第一式,再利用KX和KY的对称性,便得

KXKY=KY

(42)

KY=(KY)T=(KXKY)T=(KY)T(KX)T=

KYKX=KX

(43)

类似地,得

YK=XK

(44)

用Y左乘等式KY=KX,并利用式(44),便得

YKY=YKX=XKX

(45)

又由于

XKX=X, YKY=Y

(46)

因此可得X=Y,表明K的加号逆是唯一的。

继而可把探测单元量测作为未知量,结合相容方程(31),可得探测单元量测的唯一极小范数解,即探测单元的伪量测

(47)

2.2目标高度补偿估计

联合式(12)、式(21)和式(22),结合上面得到的伪量测,可得岸海空协同探测量测方程[16-17]为

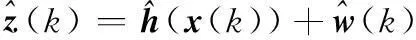
(48)

式中

(49)

(50)

(51)

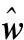
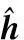
(52)

3算法仿真验证与分析

为验证所提出算法的有效性,本文对该算法的执行情况进行了仿真。

仿真系统的构成为:一部岸基雷达、一艘驱逐舰、一架预警机、一架敌方飞机以及一个协同中心节点,并且敌方飞机处于预警机雷达、驱逐舰雷达以及岸基雷达的共视区域内。

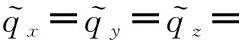
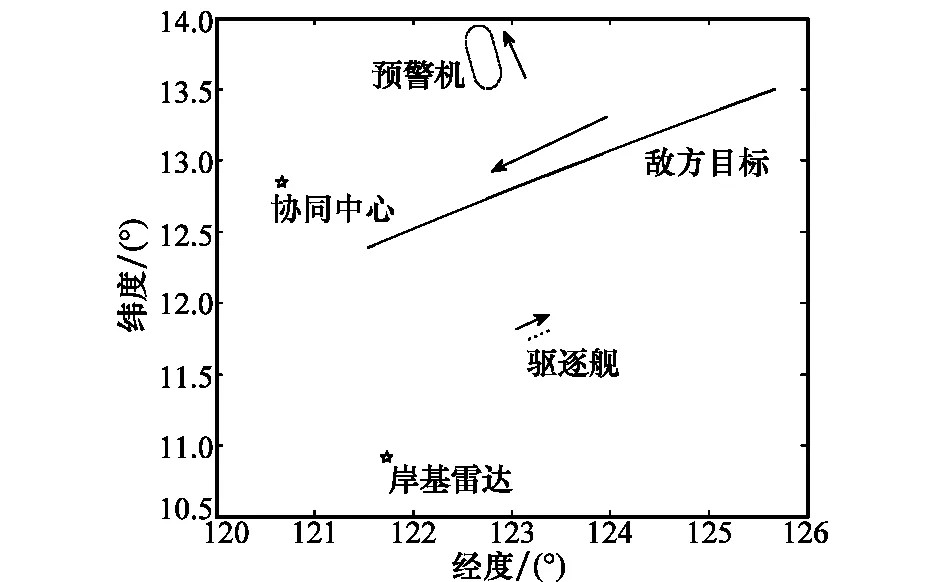
图1　仿真环境经纬图

当目标巡航海拔高度为10 000m时,岸海空探测单元对目标的共同探测时间为1 582s,岸海空探测单元各自独立跟踪结果、岸海空探测单元协同跟踪结果如图2～图4所示。

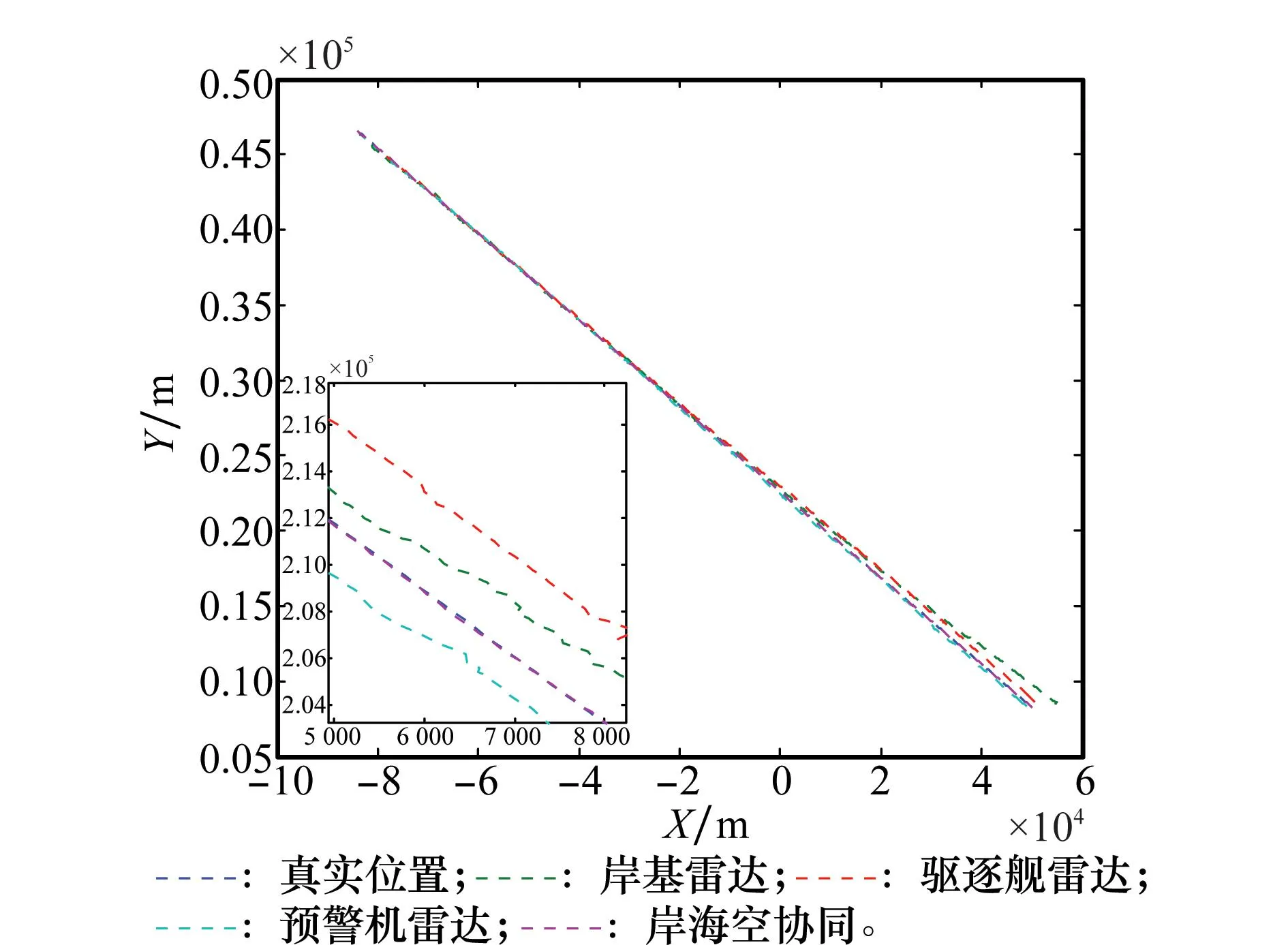
图2　岸海空协同FT坐标系XY平面跟踪结果比较

图3　岸海空协同FT坐标系Z轴方向跟踪结果比较

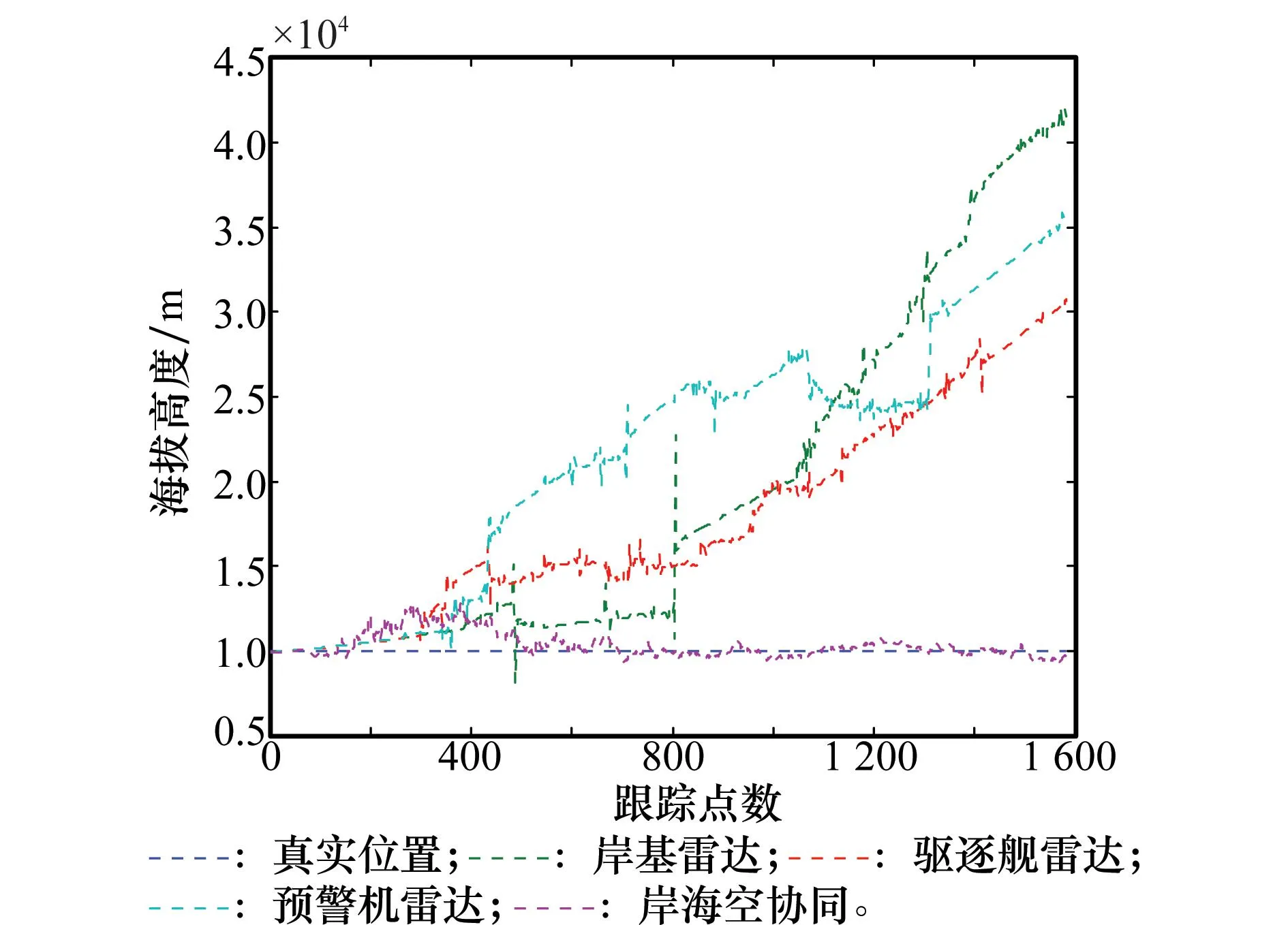
图4　岸海空协同目标海拔高度估计结果比较

由图2和图3可知,由于目标俯仰信息的缺失,单个探测单元对目标状态的估计是存在一定偏差的,其中在FT坐标系XY平面的偏差较小、Z轴方向偏差较大,且目标离探测单元越近,偏差越大越明显。此时单个探测单元仅能实现目标的预警,无法提供火控级目标定位信息和目标属性信息。通过岸海空协同探测,利用各探测单元上传的目标航迹报信息,可实现目标的无偏状态估计,且估计精度较高。由图4可知,本文给出的算法可实现目标海拔高度相对准确的补偿估计,估计精度可满足目标属性判别以及火力打击的需要。

下面通过蒙特卡罗仿真如图5～图7所示,进一步对本文算法对目标状态和目标海拔高度的估计性能进行量化研究。

由图5～图7可知,各探测单元对目标的跟踪均方根误差在FT坐标系XY平面最大可达4km,在Z轴和目标海拔高度上的估计误差最大可达20km,而岸海空协同跟踪的均方根误差在XY平面维持在30～150m范围内,在Z轴和目标海拔高度上的估计误差都维持在100～1 800m范围内,精度较高。可见通过岸海空协同融合处理,目标跟踪精度提高明显,在XY平面内,精度可达100m左右,可满足火控需求,在Z轴和目标海拔高度上的估计精度可达1km左右,可满足目标属性判别以及威胁判断的需求。

图5　岸海空协同XY平面跟踪均方根误差比较

图6　岸海空协同Z轴方向跟踪均方根误差比较

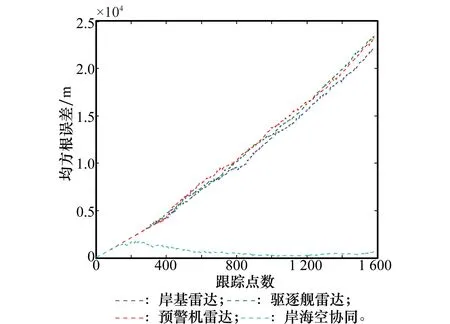
图7　岸海空协同目标海拔高度估计均方根误差比较

下面仿真分析目标处于不同巡航高度时,本文算法对目标高度的补偿估计性能。当目标巡航海拔高度为5 000m时,岸海空探测单元对目标的共同探测时间为1 139s,当目标巡航海拔高度为2 000m时,岸海空探测单元对目标的共同探测时间为583s,如图8和图9所示。

由图8和图9可知,当目标的巡航高度为5 000m时,岸海空协同对目标高度的补偿估计精度可达1km左右,当目标的巡航高度为2 000m时,岸海空协同对目标高度的补偿估计精度可达500m左右,都能满足目标属性判别的需要,因此本文提出的算法对目标巡航高度具有很强的适应性,可用于解决任意高度飞行目标的高度补偿问题。

本文仿真平台基于PC实现,其CPU采用Intel公司生产的8核心Core系列CPU,型号为i7-4710MQ,工作主频2.5GHz,内存采用三星公司生产的内存条,单条容量4GB;硬盘采用希捷公司生产的7 200pm、500GB机械硬盘,C盘容量100GB,操作系统为64位Windows7旗舰版。

图10为本文高度估计算法运算量统计情况。从图中可以看出,50次蒙特卡罗仿真共计耗时2.28s,单次运算约耗时44ms,运算量较低,实时性较好。

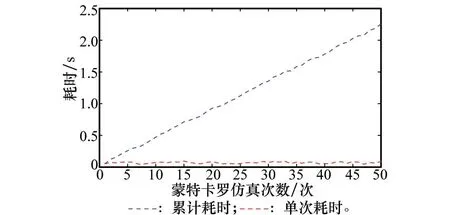
图10　高度估计算法运算量统计

4结论

本文主要研究了岸海空协同探测目标高度补偿估计技术。针对现有高度估计算法缺乏对实际多雷达组网系统特点和信息处理流程的考虑、仅能对探测单元的原始量测进行处理等不足之处,本文在我岸海空协同预警体系下,从信息处理流程和信息处理方法两个方面,对探测单元信息缺维情况下的目标高度补偿问题开展了研究。在信息处理流程方面,结合岸海空协同组网特点,设计了如下处理流程:首先探测单元各自分别对目标进行缺维有偏跟踪;然后上传实时目标航迹报到协同中心;最后在协同中心,利用各探测单元上传的航迹信息,实现目标状态的无偏估计,即目标高度的补偿估计。在信息处理方法方面:首先根据岸基雷达LH量测坐标系、舰载雷达和机载雷达的VVLH量测坐标系与协同中心FT坐标系间的变换关系,并利用扩展卡尔曼滤波技术,在协同中心FT坐标系中分别构建了岸海空探测单元对目标的缺维有偏估计方程组,实现了各探测单元在协同中心FT坐标系中对目标的跟踪;其次根据目标的缺维有偏估计方程组,通过理论证明和公式推导,构建了利用探测单元上传航迹报来求取探测单元原始伪量测的反解方程;最终基于求解的岸海空探测单元原始伪量测,构建出岸海空探测单元联合量测方程,然后进一步采用扩展卡尔曼方程组对目标状态进行估计,得到了目标的无偏状态估计,从而实现了目标高度的补偿估计。

仿真结果表明，本文给出的信息处理流程和相应的算法可在目标量测信息缺维情况下,在协同中心实现目标状态的无偏、精确估计,可满足目标预警以及火力反击的需要,得到的目标海拔高度估计结果,可满足目标属性判别和威胁判断的需要。另外仿真验证表明，本文算法对目标巡航高度具有很强的适应性,可用于解决任意高度飞行目标的高度补偿问题。

参考文献：

[1] He Y, Xiu J J, Zhang J W,et al.Radardataprocessingandapplication[M]. 3rd ed.Beijing:Publishing House of Electronics Industry, 2013: 110-130. (何友, 修建娟, 张晶炜,等. 雷达数据处理及应用[M]. 3版.北京:电子工业出版社, 2013: 110-130.)

[2] He Y, Wang G H, Peng Y N, et al.Multi-sensorinformationfusionwithapplication[M].2nd ed. Beijing:Publishing House of Electronics Industry,2007:225-240.(何友,王国宏,彭应宁, 等. 多传感器信息融合及应用[M]. 2版. 北京:电子工业出版社, 2007:225-240.)

[3] Takabayashi Y, Obata Y, Kurazume R. Altitude estimation using particle filter with monopulse radars in a multipath environment[C]∥Proc.oftheIEEEInternationalConferenceonAdvancedIntelligentMechatronics, 2015: 202-207.

[4] Stamatescu G, Stamatescu I, Popescu D, et al. Sensor fusion method for altitude estimation in mini-UAV applications[C]∥Proc.ofthe7thElectronics,ComputersandArtificialIntelligenceConference, 2015: 25-27.

[5] Lei Y, Feng X X, Zhu C B, et al. Estimation of aircraft altitude with 2D radar intelligence networking[J].FireControl&CommandControl,2011,36(12):157-159.(雷雨,冯新喜,朱灿彬,等.2D雷达情报组网目标高度估计[J].火力与指挥控制,2011,36(12):157-159.)

[6] Zhao K R, Zhou G J, Yu C J, et al. Estimation of flight altitude in high frequecy surface wave radar[J].SystemsEngineeringandElectronics, 2012，34(8) : 1571-1575. (赵孔瑞,周共健,于长军,等. 高频地波雷达飞行目标高度估计[J].系统工程与电子技术,2012，34(8): 1571-1575.)

[7] Rakvongthai Y, Ru J, Sivananthan S, et al. Altitude estimation for 3-D tracking with two 2-D radars[C]∥Proc.ofthe14thInternationalConferenceonInformationFusion, 2011: 1-8.

[8] Poullin D, Flecheux M. Passive 3D tracking of low altitude targets using DVB (SFN Broadcasters)[J].AerospaceandElectronicSystemsMagazine, 2012, 27(11): 36-41.

[9] Sun J, Shang S, Xu J D. 3D shape reconstruction from 2D ISAR measurements[C]∥Proc.oftheInternationalConferenceonWaveletActiveMediaTechnologyandInformationProcessing, 2012:25-28.

[10] Rosebrock J. Absolute attitude from monostatic radar measurements of rotating objects[J].IEEETrans.onGeoscienceandRemoteSensing,2011, 49(10): 3737-3744.

[11] Luo Z Y, He J Z. Least-square estimation of true height in 2-D radar networking[J].CommandControl&Simulation,2007,29(3):41-44.(罗志勇,何佳洲.2D组网雷达目标真实高度的最小二乘估计[J].指挥控制与仿真,2007,29(3):41-44.)

[12] Wei X Q, Song S M. Cubature Kalman filter-based satellite attitude estimation[J].JournalofAstronautics,2013,34(2): 193-200. (魏喜庆,宋申民. 基于容积卡尔曼滤波的卫星姿态估计[J].宇航学报, 2013,34(2): 193-200.)

[13] Safari S, Shabani F, Dan S. Multirate multisensor data fusion for linear systems using Kalman filters and a neural network[J].AerospaceScienceandTechnology, 2014, 39: 465-471.

[14] Gao W, Li J, Yu F, et al. Data fusion with two nonlinear constraints on Kalman filtering[C]∥Proc.ofthePosition,LocationandNavigationSymposium-PLANS, 2014: 524-528.

[15] Wichit N, Choksuriwong A. Multi-sensor data fusion model based Kalman filter using fuzzy logic for human activity detection[J].InternationalJournalofInformationandElectronicsEngineering, 2015, 5(6): 450-454.

[16] Pierleoni P, Belli A, Palma L, et al. An accurate device for real-time altitude estimation using data fusion algorithms[C]∥Proc.ofthe10thInternationalConferenceonMechatronicandEmbeddedSystemsandApplications, 2014: 1-5.

[17] Yi W, Morelande M R, Kong L, et al. A computationally efficient particle filter for multitarget tracking using an indepen-dence approximation[J].IEEETrans.onSignalProcessing, 2013, 61(4): 843-856.

[18] Bocquel M, Driessen H, Bagchi A. Multitarget particle filter addressing ambiguous radar data in TBD[C]∥Proc.oftheIEEERadarConference, 2012:575-580.

[19] Wang G H, Xu J F, Mao S Y, et al. On the CRLB of height estimation in a 2-demensional-radar-based network[J].ActaAeronauticaetAstronauticaSinica,2004,25(1):66-68.(王国宏,许建峰,毛士艺,等. 2D雷达组网中目标高度估计误差的Cramér-Rao限[J].航空学报, 2004,25(1): 66-68.)

[20] Zhong X, Premkumar A B. Particle filtering approaches for multiple acoustic source detection and 2-D direction of arrival estimation using a single acoustic vector sensor[J].IEEETrans.onSignalProcessing, 2012, 60(9): 4719-4733.

[21] Aoki E H. A general approach for altitude estimation and mitigation of slant range errors on target tracking using 2D radars[C]∥Proc.ofthe13thConferenceonInformationFusion, 2010: 1-8.

[22] Amato F, Golino G. Accuracy of height estimation by a system of 2-D netted radars[C]∥Proc.oftheIEEECIEInternationalConferenceonRadar, 2011:773-776.

[23] Jones G, Weber P, Nohara T J. 3D radar using augmented 2D hardware—sampling and processing concepts[C]∥Proc.ofthe8thInternationalWorkshoponSystems,SignalProcessingandtheirApplications, 2013: 421-428.

[24] Jevtic M, Markovic K, Pajic T, et al. Track-to-track fusion module for network-centric air surveillance applications[C]∥Proc.ofthe22ndIEEETelecommunicationsForumTelfor, 2014: 585-588.

司记伟(1986-),男,博士研究生,主要研究方向为目标检测与识别、多传感器信息融合。

E-mail:sijiweide@126.com

田燕妮(1978-),女,博士研究生,主要研究方向为雷达信号处理。

E-mail:tianyanni@126.com

潘莉莉(1980-),女,助理研究员,硕士,主要研究方向为雷达信号处理。

E-mail:735311973@qq.com

刘思琦(1987-),女,助理讲师,主要研究方向为电气化技术、数据处理。

E-mail:309833420@qq.com

Research on technique of compensative estimation of target height in shore, sea and air collaborative defense system

SI Ji-wei1, TIAN Yan-ni2, PAN Li-li1, LIU Si-qi3

(1.DepartmentofScientificandResearch,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China; 2.Unit92857ofthePLA,Beijing100161,China; 3.DepartmentofElectricalEngineering,ZhangjiakouVocationalCollegeofTechnology,Zhangjiakou075000,Chinia)

Abstract:Aiming at the existing target height estimation algorithms’ deficiencies that the lack of consideration for the information processing flow in the real multi-radar network would make the algorithms hard to be applied in the practical system, the problem that how to effectively compensate for target height in the presence of the incomplete measurement is studied from the two aspects of information processing flow and the information processing approach under the shore, sea and air collaborative defense system. The simulation result shows that the proposed algorithm can obtain the unbiased, stabilize and accurate estimate of the target state which can meet the need of target attribute identification and threat evaluation. At the same time, the simulation verifies that the algorithm is highly adaptable to the target cruising altitude and can solve the height compensation problem of the target which flies in the same observation of shore, sea and air detect units at any altitude.

Keywords:collaborative defense; height compensation; pseudo measurement; extend Kalman filter

收稿日期：2015-03-14；修回日期：2015-09-08；网络优先出版日期：2015-11-18。

基金项目：国家自然科学基金重点项目(61032001)资助课题

中图分类号：TP 953; TN 957

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.05

作者简介：

网络优先出版地址：http:∥www.cnki.net/kcms/detail/11.2422.TN.20151118.1207.004.html