基于类型2区间模糊K近邻分类器的动态武器-目标分配方法研究

王　邑, 孙金标, 肖明清, 罗继勋

(1. 空军指挥学院战术系, 北京 100097; 2. 空军工程大学航空航天工程学院, 陕西 西安 710038)



基于类型2区间模糊K近邻分类器的动态武器-目标分配方法研究

王邑1, 孙金标1, 肖明清2, 罗继勋2

(1. 空军指挥学院战术系, 北京 100097; 2. 空军工程大学航空航天工程学院, 陕西 西安 710038)

摘要：动态武器-目标分配问题是战场指挥控制决策中的关键问题。由于动态武器-目标分配算法是在攻击间隙所做的决策,对计算时间的实时性要求较高。解决这一问题,可以采用机器学习的方法基于战场辅助决策系统的武器-目标分配,从已知的决策中推理生成出新的决策,而不必每个步骤中都重新搜索新的目标分配方案。根据这种思路,提出了一种基于类型2区间模糊K近邻分类器的武器-目标分配方法,利用分支定界法得到的分配方案作为训练样本,通过构造并行运行的类型2区间模糊K近邻分类器来推导目标分配结论,实现了快速决策的目的。

关键词：战术决策; 武器-目标分配; 类型2区间模糊K近邻分类器; 机器学习

0引言

武器-目标分配问题(weapon-target assignment, WTA)是战场指挥决策中的关键问题[1]。目前,研究重点在如何解决动态武器-目标分配问题上[2],即假设武器对威胁的分配是根据前一轮攻击战果的总结来得到的,考虑某个离散时间段的武器-目标分配,并必须在下一轮攻击之前给出明确的分配方案。这种在攻击间隙中进行的观察、决策、执行过程,其时间非常有限,因此,动态的武器-目标分配的解算时间应该在尽量短,越接近实时越好,这样,所有的行动才能与任务目的和战场环境约束相一致。

武器-目标分配问题通常被形式化为一类非线性整数规划问题。该整数规划是典型的NP完全问题[3],目前典型的解法分为解析解法和启发式解法两大类[4]。解析解法采用动态规划的思路,通过全枚举来得到最优分配方案。典型的方法如割平面法[5]、分支定界法[5]等。通常可以得到问题的全局最优解,但其计算效率太低,且枚举数量随问题规模上升呈指数上升,无法进行实时解算;启发式解法从搜索算法上对目标分配的问题域进行有效地规划,利用启发式的搜索策略,在不进行全枚举的前提下搜索理想的解,如遗传算法[6]、模拟退火[7]、粒子群优化[8]、TABU搜索[9]、遗蚁群算法[10]等。

基于搜索的方法在每次使用时都需重新计算。但对于动态武器-目标分配而言,在相邻的时间片上,战场态势可能并未产生剧烈变化,重新计算带来了相当大的运算压力,还限制了解析解法的实用价值。采用机器学习方法中的监督学习方法,能够避免重复计算的问题。机器学习方法与搜索算法不同,构建算法与应用算法的时间不对称,在针对决策过程进行相应的建模,即训练过程后,模型的实际推理过程很快,推理的速度大大地优于重新搜索的速度。

本文提出一种用机器学习理论来解WTA问题的方法,该方法利用了精确解法的精度高、启发式方法速度快的优点,用精确解构造决策模型,对从解空间到精确解的判定过程进行近似,然后实时推理出WTA问题的分配方案。采用模式分类器作为问题的核心算法,根据目标与武器的决策变量,抽象出一定的模式,将不同的目标分配方案与不同的模式对应,然后当输入的问题参数满足某一模式的特征以后,就输出对应的目标分配方案。

分类器算法选用区间类型2模糊K近邻(interval type-2 fuzzy K-nearest neighbor,IT2FKNN)分类器,K-近邻(K-nearest neighbor, KNN)算法是一种结构简单,效率较高的分类器,其计算速度很快,采用多个KNN实现并行计算简单,加上采用基于区间类型2模糊集的扩展算法对重合特征、不确定性特征的区分识别能力进一步增强,总体算法的效果得到加强。

本文采用随机数字仿真实验验证了方法的性能。实验了3×4、8×16、60×120等3个WTA问题,在实际战役仿真系统中,同时规划武器的数量突破100以上的问题可定位为大规模WTA问题[11],这3个问题分别属于小、中、大规模问题。通过仿真实验,本文方法的性能满足预期,对于小、中、大规模问题都能在有限时间内快速地解决。本研究为在大规模兵力调配中使用相关方法提供了基础。

1方法架构及实现

1.1问题描述

武器-目标分配问题的标准描述可分为进攻型和防御型两种[12],其中进攻型考虑了我方的打击效果及目标的价值,防御型考虑敌我双方的打击效果及我方作战单元的价值。由于这两种表述可以相互变换,且研究中采用较多的是进攻型表述,所以,本文中以进攻型模型作为研究问题的描述,其可以由以下非线性整数规划问题所描述[13]:

(1)

s.t.

(2)

目标函数式(1)为最小化目标的价值期望,限定条件式(2)为保证武器至少且至多被分配至一个目标,武器-目标的分配方案中可以存在某个目标同时被多个武器分配或无武器分配的情况,但不存在某一武器不被分配目标的情形。|T|表示目标的数量,|W|表示武器的数量,因为不考虑单个武器的多目标分配,故设定武器数量大于或等于目标数量。Vi是目标Ti的价值,Pik是武器Wk对于目标Ti的杀伤概率,dik是决策变量,当指派武器Wk打击目标Ti时为1,其余时为0。若假设Vi=pi(t)·wi,pi(t)为在t时刻目标Ti的生存概率,且wi为该目标的价值,对式(1)、式(2)的不断求取就是对动态武器-目标分配问题的求解。

1.2算法概述

算法的基本形式为

(3)

式中,算法的输入为向量x;输出为向量y;计算中所用训练集由向量xtr,ytr组成。由于算法的决策依据为式(1)中的Vi和Pik。设目标数量|T|=I,武器数量|W|=K,则算法的输入为以下I+IK维向量:

(4)

算法的输出为IK维决策向量:

(5)

若将y按K拆分,则得到对应于K个武器的目标分配向量yk,y=[y1,…,yk,…,yK]

每个向量为I维,由于每个武器只能分配一个目标,则yk向量的所有取法为I+1个,一一对应于分配i种目标(第i维为1,其余为0)或不分配目标(全为0),若将这I+1种取法看作是类别信息,则算法式(3)可被看做是K个分类器,输入向量为I+IK维,输出为标量类型yk。以上的讨论中可见,武器-目标分配问题可看做是一个分类问题。

图1为算法结构图。图中采用了多个区间类型2模糊K近邻算法对每个武器的目标分配方案进行解算,实际上将输出分割为K个子集,采用这种采用瀑布型并行构造的决策模型,每个模型只考虑类型数量为I+1的分类问题,这就降低了分类的复杂度,在一定程度上避免了输出过于复杂的问题。而且,若武器对于攻击对象的类型是有选择的情况下,即yk的所有取值数量少于I+1,在这种结构下产生的分类类别将更少。

图1　算法结构图

本文提出的方法中,采用分支定界法这种确切解法所产生的方案来构造训练集。当问题规模变化时,训练数据必须相应变化。为了降低重构训练数据的计算时间,可以构造多个可能的对抗关系,并对应地训练多个决策模型,一旦对抗关系发生了改变,分配问题中的对抗规模发生变更,则切换为备选的决策模型。这种方法在战场上的使用的实时性和稳健性较好,但是需要很大的存储空间来存储和调用多个模型;另一种思路是只训练一个决策模型,始终保持目标的数量与我方武器数量相同,这样在实际运用中,当遇到实际目标多于我方武器数量时,则采用价值排序的方式,优先选择价值较高的t个目标进行分配。当目标数量小于I时,例如目标数量为Ir,则在分配时将I-Ir个目标的价值设为0。

1.3区间类型2模糊K近邻算法

区间类型2模糊K近邻算法(IT2FKNN)是在KNN[14]的基础上发展而来的。KNN通过将样本与聚类间的距离进行比较,产生K个最近聚类,其最多数聚类与已知的分类规则的对应关系,构成了分类的依据,在实际使用中可以发现,在维持一定的分类精度的前提下,KNN计算速度要远高于其他比较复杂的算法,因此在处理WTA问题中非常适用。然而,标准KNN算法的最大问题是,已知分类知识中对应的聚类必须是相同重要度的互相区分的聚类。因此,当聚类元素存在重叠关系的时候,用KNN方法就无法进行正确的分类。为克服这个缺陷,学者引入了模糊隶属函数来描述聚类与类型的关系,即FKNN算法[15],很大地提高了分类的精度,并能够处理类型存在交叉重叠的分类问题。然而,FKNN算法对于K的选择存在不足,不同的K值选取对结果的影响比较大,且K值没有一个先验的计算公式能够解出,因而,影响了其整体的分类精度。因此,本文引入利用区间类型2模糊集来描述的KNN算法,即IT2FKNN[16]。在FKNN中,初始值K为单值,一次计算只围绕一个初始K值来指派聚类数据的初始模糊隶属函数,若初始K值选取得不合理,则分类的结果就不合理。而IT2FKNN由于采用的是区间类型2模糊集,初始K不为单值,则可以合理地避免此类问题的发生。

IT2FKNN的隶属度指派公式为

(6)

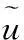
在式(6)中,样本x的隶属函数是其K个临域样本距离成反比,并与该样本的隶属度相关。式中对于初始隶属度的求法,可以参照内置区间类型2模糊集的运算[17],例如,假设K=2,需两个近邻样本的主要隶属度作为边界,并从中得到两个主要隶属度之间对应的内置区间类型2隶属函数。

通过K个临域聚类的主要隶属函数,来间接得到xk的主要隶属函数,假设每个聚类有nj个主要隶属度,则xk的隶属度规模,即参与交集运算的隶属函数数量,计算公式为

(7)

式中,K表示聚类数；i表示类型数。

从式(7)可以得到样本xk的主要隶属度为

(8)

根据类型2模糊集的定义[17],样本xk的次要隶属度为1。所以,样本xk的类型2隶属函数可以写作:

(9)

从式(8)和式(9)的推导中,得到了样本xk的类型2隶属函数,即为聚类指派了类型2模糊隶属度,对于分类来说,最后计算中要得到确切的隶属度数字,首先要求这个类型2模糊隶属函数,对其进行降型运算,后进行标准的去模糊化运算。

降型计算如下:

对于xk和类型i,其降型后的隶属函数为

(10)

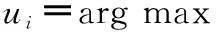
IT2FKNN算法的步骤如下:

步骤 1给定Ik={k1,k2,…,ks},即K值的组合;

步骤 3根据式(6)计算未知样本的隶属度;

2仿真实验

实验所用算法采用C++实现,分类器采用OpenMP共享内存并行计算框架,计算机采用CPU为运行于2.4GHz的8核处理器,为了便于研究复现,采用随机生成的测试数据进行性能评价。实验采用了多步判断法,随机的敌我双方位置、杀伤评价指标矩阵、累积生存概率及重要程度信息。

2.1仿真数据生成方法

数据生成算法的基本情况如下:

武器数量为K,|W|=K,W={W1:k};

目标数量为I,|T|=I,T={T1:i};

目标生存价值:Vi=piwi,其中,pi取目标ti累积生存概率,wi为目标ti对应的价值,设为只与敌距我战略部署的中心距离ri有关,rmaxi为想定的敌我最大距离:

(11)

当连续计算多步WTA时,武器与目标的距离由目标相对速度Δvi、目标相对距离ri(τ-1)经递归计算得到,计算式为

(12)

武器毁伤效果按照加权的钟形函数来取:

(13)

式中,aik是武器对目标的经验杀伤概率;钟形函数的宽度参数取常量rc;rBik是武器对目标具有最大杀伤概率时的距离;ε是人工加的扰动。

2.2实验参数设置

实验参数设置如表1和表2所示。

表1　实验1参数设置

仿真中取样1 000次,每一次取样都得到一个目标的距离向量。对于每个取样,按照式(13)评估目标价值和武器杀伤概率,产生[V1∶I,P1∶I,1∶k]1∶1 000用分支定界法计算对应的决策[d1∶i,1∶k]1∶1 000,这样就形成了实验数据。

表2　实验2、实验3参数设置

为了验证算法的效果,采用KNN[14]、FKNN[15]、分支定界法[5]和遗传算法[6]作为对比算法。分支定界法和遗传算法及本文的方法可以按照算法计算时间和优化性能两方面来进行比较。各引用算法均按照原论文中的描述进行构建。在计算算法的估计误差时,采用10重互校验(10-foldcrossvalidation),将数据样本集随机分割成不相交的10个子集,依次选取其中一个作为训练集〈xtr,ytr〉,再随机选取另一个子集作为验证集,这样对算法验证检验10次,取其平均值。

对于分类算法,验证指标为其分类正确率:

(14)

另一验证指标是代价值误差率,即精确解与近似解的代价之差,除以精确解的代价来归一化,即

(15)

式中,E(x,y)是整数规划问题(1)中的目标函数。

3仿真结果分析

3项仿真实验均进行了103次,仿真结果如表3所示。通过结果可以看出,相比分支定界法和GA法,IT2FKNN能够得到满意的近似效果,且计算时间相比分支定界法要短得多,这与预期相同。由于IT2FKNN采用了并行处理的方式,因此多个分类器的计算时间理论上趋近于一个分类器的时间,而反之分支定界法和遗传算法随随规模增大,其代价函数的计算量显著增加,而复杂度极具增大,因为搜索类算法在每一个循环中都要重新计算代价函数,所以其计算时间可能较长。而机器学习算法一旦训练完成,其计算时间几乎可以忽略不计。在训练中,算法的并行解算机制及不依赖代价函数的性质,使其更适于处理较大规模的目标分配问题。除此以外还可以看出,本文方法在大规模问题上计算时间依然较快,适用于解大规模问题。但由于分支定界法的运算时间太长,因此在大规模问题的实际应用中,宜将本文方法与启发式搜索方法相结合,采用启发式搜索方法的输出作为训练样本,这样才能保证方法应用的实时性。

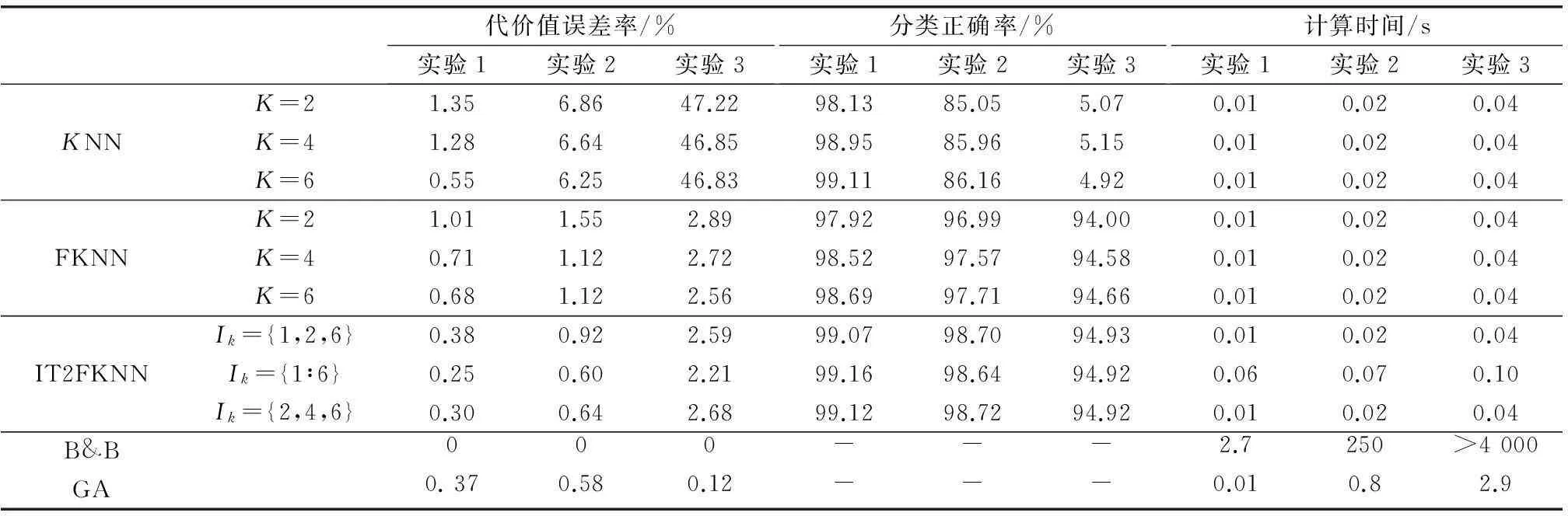
表3　仿真实验结果

4结论

在本研究中,提出了一种战场上辅助决策算法,即通过基于规则的映射来机器学习过程,达到目标分配的意图。此方法是机器学习在武器-目标分配问题研究中的有益尝试,该方法在一定程度上保证分配精度而且计算时间较快。

目前针对动态武器-目标分配问题的方法较多,各有其适用范围,本研究所述方法最适用于战场运筹时间片之间,态势未发生剧烈变化情况下的快速计算,在态势剧烈变化,不确定性迅速上升的情况下,可结合其他方法,例如采用鲁棒的分配策略抑制不确定性、裁剪战场态势条件、多模型决策、预判断与预处理等,以得到更好的运算效果。

本研究中,尚有两方面的问题未作讨论,可以留作后续研究。一是,没有讨论各武器在目标分配方案中的统计联系及组合分配方案,例如若A分配目标a,则B必分配目标b,或更进一步,将武器和目标结合成组,只考虑(AB)分配(ab)的情形,这涉及到将分配方案本身作为训练的问题域变量带入计算,以及挖掘武器作战效能的关联性关系问题。二是,没有讨论分类器本身的数据挖掘和性能优化,例如,通过分析,得到问题域的经验维度,然后按照值来设计分类器,采用数据降维或特征选取/提取算法,将问题域压缩为进行运算,这样分类器的训练时间预期将显著缩短,但特征提取是与实际情况相关的,还需要结合问题域数据的基本特征做进一步分析。

参考文献：

[1] Liu C B, Qiu Z M, Wu L, et al. Review on current status and prospect of researches on dynamic weapon target assignment[J].ElectronicOptics&Control, 2010, 17(11): 43-48. (刘传波, 邱志明,吴玲,等.动态武器-目标分配问题的研究现状与展望[J].电光与控制,2010,17(11):43-48.)

[2] Cai H P, Chen Y W. The development of the research on weapon-target assignment (WTA) problem[J].FireControlandCommandControl, 2007, 31(12): 11-15. (蔡怀平, 陈英武. 武器-目标分配 (WTA) 问题研究进展[J].火力与指挥控制, 2007, 31(12): 11-15.)

[3] Huang F, Chen Z Q, Feng J F, et al. Target assignment algorithm for air-to-ship missile based on semi-restraint stochastic searching[J].SystemsEngineeringandElectronics,2013,35(8):1676-1680.(黄峰,陈中起,冯金富,等.基于半约束随机搜索的空舰导弹目标分配方法[J].系统工程与电子技术,2013,35(8):1676-1680.)

[4] Xin B, Chen J, Zhang J, et al. Efficient decision makings for dynamic weapon-target assignment by virtual permutation and tabu search heuristics[J].IEEETrans.onSystems,Man,andCybernetics,PartC:ApplicationsandReviews, 2010,40(6):649-662.

[5] Ahuja R K, Kumar A, Jha K C, et al. Exact and heuristic algorithms for the weapon-target assignment problem[J].OperationsResearch, 2007, 55(6): 1136-1146.

[6] Malhotra A, Jain R K. Genetic algorithm for optimal weapon allocation in multilayer defence scenario[J].DefenceScienceJournal, 2002, 51(3): 285-293.

[7] Liu S W, Wang J, Yang M, et al. Research of ACO-SA optimization strategy for solving target assignment problem in air-defense C^3I system[J].SystemsEngineeringandElectronics, 2008, 29(11): 1886-1890. (刘少伟, 王洁, 杨明, 等. 防空 C^3I 目标分配问题的 ACO-SA 混合优化策略研究[J].系统工程与电子技术, 2008, 29(11): 1886-1890.)

[8] Fan C L, Xing Q H, Zheng M F, et al. Weapon-target allocation optimization algorithm based on IDPSO[J].SystemsEngineeringandElectronics,2015,37(2):336-342.(范成礼,邢清华,郑明发,等.基于IDPSO的武器-目标分配优化算法[J].系统工程与电子技术,2015,37(2):336-342.)

[9] Xu J Q, Bi Y M, Wang M L, et al. Modeling and realization of conventional missile fire assignment based on time-space restriction[J].SystemsEngineeringandElectronics, 2011, 33(9): 2025-2029.(徐加强,毕义明,汪民乐,等.基于时空约束的常规导弹火力分配建模与实现[J].系统工程与电子技术,2011,33(9):2025-2029.)

[10] Huang S C, Li W M. Research of ant colony algorithm for solving target assignment problem[J].SystemsEngineeringandElectronics,2005,27(1):79-80.(黄树采,李为民.目标分配问题的蚁群算法研究[J].系统工程与电子技术,2005,27(1):79-80.)

[11] Murphey R A.Target-basedweapontargetassignmentproblems[M].US:Springer,Nonlinear Assignment Problems,2000:39-53.

[12] Paradis S, Benaskeur A, Oxenham M, et al. Threat evaluation and weapons allocation in network-centric warfare[C]∥Proc.ofthe8thIEEEInternationalConferenceonInformationFusion, 2005.

[13] Hosein P A. A class of dynamic nonlinear resource allocation problems[R]. Massachusetts: Massachusetts Institute of Technology Cambridge Lab for Information and Decision Systems, 1989.

[14] Weinberger K Q, Blitzer J, Saul L K. Distance metric learning for large margin nearest neighbor classification[C]∥Proc.oftheAdvancesinNeuralInformationProcessingSystems,2005:1473-1480.

[15] Kuncheva L I.Fuzzyclassifierdesign[M]. Springer Science & Business Media, 2000.

[16] Darwish S M, El-Zoghabi A A, Hassen O A. A modified walk recognition system for human identification based on uncertainty eigen gait[J].InternationalJournalofMachineLearningandComputing, 2014, 4(4): 346.

[17] Mendel J M, John R, Liu F. Interval type-2 fuzzy logic systems made simple[J].IEEETrans.onFuzzySystems, 2006, 14(6): 808-821.

王邑(1984-),男,工程师,博士,主要研究方向为计算智能、空军合同战术模拟。

E-mail:wangyiafcc@hotmail.com

孙金标(1964-),男,教授,博士研究生导师,博士,主要研究方向为空军战术学。

E-mail:sunjinbiao@sohu.com

肖明清(1963-),男,教授,博士研究生导师,博士,主要研究方向为武器系统检测智能化与自动化。

E-mail:xmqing@163.com

罗继勋(1967-),男,副教授,硕士研究生导师,博士,主要研究方向为航空武器作战效能分析。

E-mail:luojxafeu@163.com

Research of dynamic weapon-target assignment problem based on type-2 interval fuzzy K-nearest neighbors classifier

WANG Yi1, SUN Jin-biao1, XIAO Ming-qing2, LUO Ji-xun2

(1.DepartmentofTactical,AirForceCommandCollege,Beijing100097,China; 2.CollegeofAeronauticsandAstronauticsEngineering,AirForceEngineeringUniversity,Xi’an710038,China)

Abstract:Dynamic weapon-target assignment (WTA) problem is one of the critical problem when processing the battlefield command control and decision. The WTA algorithm makes the decision at the gap of two attack periods, which needs to be calculated efficiently.When using the battlefield assistant system to make WTA decision, it is a reasonable concept to utilize the machine learning method, make new decision from the known decision to avoid the need of searching new target assignment all over again. By using this concept, an interval type-2 fuzzy K-nearest neighbors(IT2FKNN) classifier usage on the WTA problem is proposed, by using the result from branch and bound to train the model, a parrallel IT2FKNN classifier is built to infer the assignment result. The proposed method is tested to be able to make a quick decision on the WTA problem.

Keywords:tactical decision; weapon-target assignment (WTA); interval type-2 fuzzy K-nearest neighbors (IT2FKNN) classifier; machine learning

收稿日期：2015-09-15；修回日期：2015-10-29；网络优先出版日期：2016-02-17。

基金项目：航空科学基金(20131789004)资助课题

中图分类号：TJ 761,V 247.2

文献标志码：A

DOI:10.3969/j.issn.1001-506X.2016.06.15

作者简介：

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160217.1143.002.html