容忍恶意攻击的无线传感网络安全定位算法

徐琨，刘宏立，詹杰，马子骥

（1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南科技大学物电学院，湖南 湘潭 411201）

容忍恶意攻击的无线传感网络安全定位算法

徐琨1，刘宏立1，詹杰2，马子骥1

（1.湖南大学电气与信息工程学院，湖南 长沙 410082；2.湖南科技大学物电学院，湖南 湘潭 411201）

针对无线传感网络中恶意攻击会篡改信标节点发射强度破坏节点准确定位的问题，提出了一种顽健的基于半定规划松弛的安全定位算法（RSRSL）。该算法将发射功率作为一个未知的变量，分别基于单目标传感网络和多目标传感网络，建立了相应的安全定位概率模型。通过将非线性非凸的定位问题转化为易于求解的半定规划问题，实现对网络中普通节点的安全定位，并分析了RSRSL算法的计算复杂度。通过仿真和实测实验对RSRSL算法进行验证，结果表明，在存在恶意攻击的环境中，RSRSL算法要明显优于已有的定位算法，具有较高的定位精度。

无线传感网络；安全定位；接收信号强度；发射功率；半定规划

1 引言

节点定位是无线传感网络（WSN,wireless sensor networks）的关键技术之一，是实现WSN其他功能的基础，一个不知道自己位置信息的节点在网络中没有任何作用[1]。在WSN中，一部分节点的位置可以通过人工预设或装备全球定位系统[2]（GPS,global positioning system）提前获得，一般称为信标节点（BN,beacon node）；但是大部分节点的位置是未知的，一般称为普通节点（SN,sensor node）。普通节点需要在网络部署之初或中途加入网络时利用信标节点进行定位，常用的定位技术有基于到达时间[3](ToA,time of arrival)、到达时间差[4](TDoA,time difference of arrival)、到达角度[5](AoA,angle of arrival)和接收信号强度[6](RSSI,received signal strength indicator)等方法。其中，基于RSSI测量值的定位方法由于实现简单、成本低廉以及不需要增加额外的硬件设备被广泛地应用到WSN定位中[7]。

基于RSSI的定位方法主要依赖接收到的信号强度值实现定位，信号强度的不确定会对定位性能产生严重的影响。目前有很多基于RSSI的定位算法，如最大似然估计法[8]（ML,maximum likelihood estimator）、线性最小二乘法[9]（LLS,linear least squares）和凸优化[10]（convex optimization）等方法。这些算法虽然能够得到较好的定位性能，但都没有考虑存在恶意攻击的情况。WSN一般部署在无人值守的区域，网络中无线信号的广播特性使信号强度很容易受到攻击者的各种恶意攻击。攻击者通过俘获信标节点发起伪造插入[11]或重放[12]等恶意攻击，虚增或虚减信标节点的发射功率值，或者采用阻挡、反射等物理攻击手段对信号进行干扰，削弱或增强信号强度，破坏网络中普通节点的正常定位，进而导致整个网络功能失效。由于能耗和成本的限制，传统网络的安全技术不能直接移植到WSN中。文献[13]提出了一种最小中值二乘算法（LMdS，least median square），通过将节点划分为多个子集过滤恶意信标节点，并利用LLS实现对节点的安全定位，但该算法的计算复杂度高。文献[14]将网络划分为网格，提出了一种过滤恶意信标节点的基于投票制（voting）的安全定位算法，通过采用迭代求精的方法实现对节点的定位，但这种方法需要将网络划分为网格，网格的大小和数量较多时，算法的计算量太大，计算复杂度高。文献[15]提出了一种基于梯度下降的安全定位算法，通过测量一致性原理过滤恶意攻击节点，实现对网络节点的定位。文献[16]提出了一种基于松弛标记方法的安全定位算法，通过检测分组内节点的行为，过滤恶意攻击节点，并证明了网络中恶意节点比例和定位精度之间的关系，当恶意节点的总数小于等于时，采用有效的定位算法可以实现准确的定位。文献[17]提出了一种分布式的基于RSSI的DPC安全定位算法，采用计算和测量一致性的原理对网络中的恶意节点进行过滤，基于簇平面的思想实现安全定位。上述算法都将安全定位过程机械地分为过滤恶意信标节点和安全定位2个阶段，增加了计算的时耗和复杂度。

针对恶意节点攻击时会虚增或虚减发射功率大小导致定位失效的问题，分别基于单目标的无线传感网络和多目标的无线传感网络，本文提出了一种顽健的基于半定规划松弛的安全定位算法（RSRSL，robust semidefinite relaxation secure localization algorithm）。该算法是一种基于顽健计算的安全定位算法，定位过程中无需过滤恶意信标节点。它不仅利用普通节点和信标节点之间的RSSI测量值，而且利用普通节点与其他普通节点之间的RSSI测量值进行位置估算。首先，建立了基于最大似然估计的定位模型；其次，针对该模型没有考虑恶意攻击会篡改发射功率的问题，提出了一种新的安全定位模型，该模型将发射功率表示成一个未知的变量，在定位过程中和位置信息一起估算，解决存在攻击时所导致的定位失效问题；然后，针对提出模型是一个复杂的非线性非凸的全局优化问题而难以求解的特点，设计了一种新的半定规划（SDP， semidefinite programming）算法，并分析了算法的复杂度；最后通过仿真和实测实验，对提出的模型和算法进行验证。

2 安全模型

基于RSSI测量值的定位算法的主要原理是依靠信号强度的路径衰减和物理距离之间的关系，求出节点之间的距离，从而实现对普通节点的定位。普通节点仅通过接收到的RSSI值实现对自身的定位，定位的精度严重依赖信标节点的发射功率。当攻击者通过重放或其他物理手段恶意篡改信标节点的发射功率后，会导致严重的定位错误，破坏网络中普通节点的定位。首先，对只有一个普通节点，m个信标节点的单目标网络进行分析，建立对应的安全定位模型；然后扩展到普遍存在的n个普通节点和m个信标节点的多目标网络，建立对应的安全定位模型。

2.1 单目标网络安全模型

首先分析只有一个普通节点时的系统模型，在这种情况下，只需考虑信标节点发送的RSSI值。考虑一个分布在二维空间的传感网络，它由1个普通节点和m个信标节点组成，每个节点都有唯一的ID，普通节点与信标节点共享一个预设密钥，实现节点间的安全通信。普通节点的位置未知，；信标节点的位置已知，。表示网络中能够与普通节点通信的信标节点集合，普通节点接收到的第j个信标节点的接收信号强度用对数正态分布模型表示为

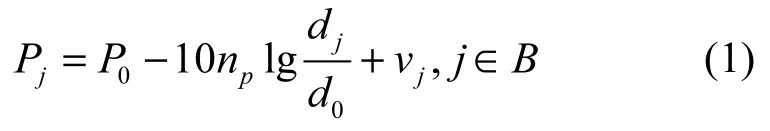
其中，Pj表示距离为dj时的接收信号强度值，单位是dBm；P0表示参考距离为d0时的接收信号强度值，一般取d0为1 m；np表示路径衰减因子；表示普通节点和第j个信标节点之间的欧氏距离；vj表示噪声干扰，它是一个均值为0，方差为的高斯随机变量。

在没有攻击的情况下，式(1)可以很好地描述网络中RSSI和物理距离之间的函数关系，但是在存在恶意攻击的环境中，攻击者可以采用重放攻击或阻挡、反射等物理攻击手段虚增或虚减攻击节点的发射功率值，这些攻击都会导致接收节点接收到的RSSI不准确，导致严重的定位错误。为了缓解恶意信标节点篡改发射功率的影响，将式(1)中的发射功率看成一个未知的变量，在计算过程中，它需要和未知节点的坐标一起被估算。因此，式(1)中将有3个需要估算的未知变量，采用加权最大似然估计模型表示对应的安全概率模型。

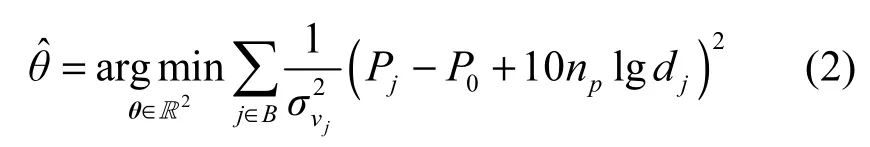
2.2 多目标网络安全模型

接下来考虑一个由n个普通节点和m个信标节点组成的网络，普通节点不仅可以和信标节点进行通信，而且能和其他普通节点进行通信，所有节点共享一个预设密钥，实现节点间的安全通信。为了提高定位性能，普通节点定位时同时利用从信标节点测量到的RSSI值和从其他普通节点测量到的RSSI值一起估算自身位置。普通节点的位置未知，。表示普通节点的集合，表示信标节点的集合。表示能和普通节点i通信的其他普通节点集合；表示能和普通节点i通信的信标节点集合。普通节点接收到的信号强度用对数正态分布模型表示为

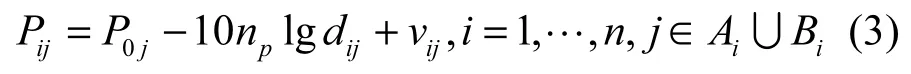
其中，Pij表示普通节点在距离为dij时的接收信号强度；P0j表示普通节点在距离为1 m处的参考接收信号强度；dij表示普通节点i和信标节点j以及其他普通节点的欧氏距离，当j∈Bi时，；当j∈Ai时，；vij表示噪声干扰，它是一个均值为0、方差为的高斯随机变量。

同样，当遇到恶意攻击时，可以将发射功率看成未知变量，用最大似然估计模型表示出对应的安全概率模型

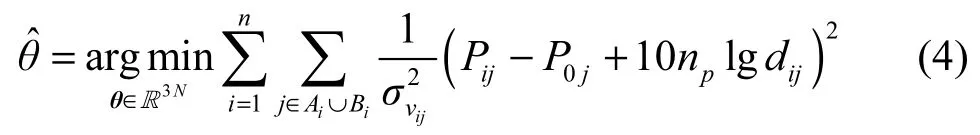
3 RSRSL算法

接下来分析如何求出安全模型式(2)和式(4)的全局最优解。针对式(2)和式(4)非线性、难于求解的问题，运用凸优化的半定规划松弛理论分别设计了式(2)和式(4)的求解算法，将对应的最大似然估计问题转化为半定规划问题进行求解。半定规划所具有的局部最优就是全局最优的特性，使其在求解过程中不会存在局部最优和鞍点的问题。下面，详细描述半定规划松弛的求解算法。

3.1 单目标网络安全定位算法

式(1)中的距离dj和功率P0都是未知变量，为了便于求解，通过取对数和对等式两边移位等操作，可以将其表示为

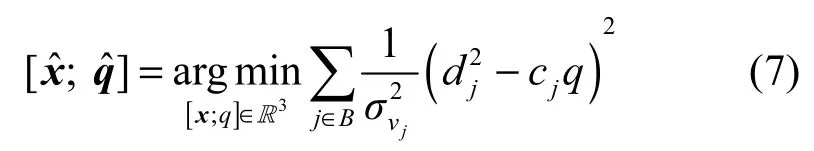
式(7)表示的定位问题和式(2)描述的问题相比虽然得到了一定的平滑，但是仍然是一个非线性非凸的优化问题，求解过程复杂，计算复杂度高。定义，将式（7）进一步转化为以下形式

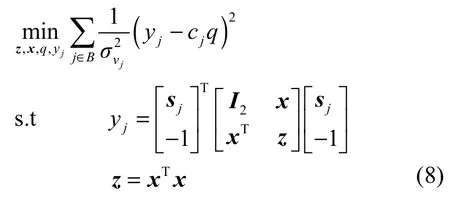
式(8)仍然表示一个非线性的优化问题。接下来，利用凸优化的松弛技术，将式(8)转化为标准的凸优化函数。将z=xTx松弛为线性矩阵不等式的形式，使让其成为一个线性形式，使求式(8)的最小化问题转化为求解半定规划问题。

采用如内点法的优化算法可以较简单地求出式(9)的最优解，而且，由于半定规划的特性，可以确保式(9)能在全局最优解处收敛。

3.2 多目标网络安全定位算法

对于存在n个普通节点的情况，可以通过和上述描述的类似方法进行求解，通过对其进行一阶泰勒级数展开并移项重新整理后，得到一个如同式(8)平滑的最大似然估计概率模型，如式(10)所示。

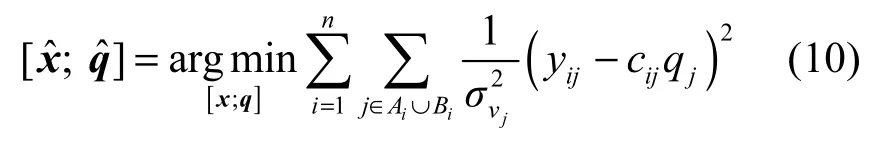
其中，q=[q1,q2,…,qm]T，和求解只有一个普通节点的方法类似，可以将式(10)采用松弛技术将其转化为求凸优化的目标函数问题。令表示普通节点坐标的矩阵，引入一个辅助矩阵变量Z=XTX，其中，表示矩阵Z的第(i,j)个元素。通过采用松弛技术，可以将式(10)转化为标准的SDP形式

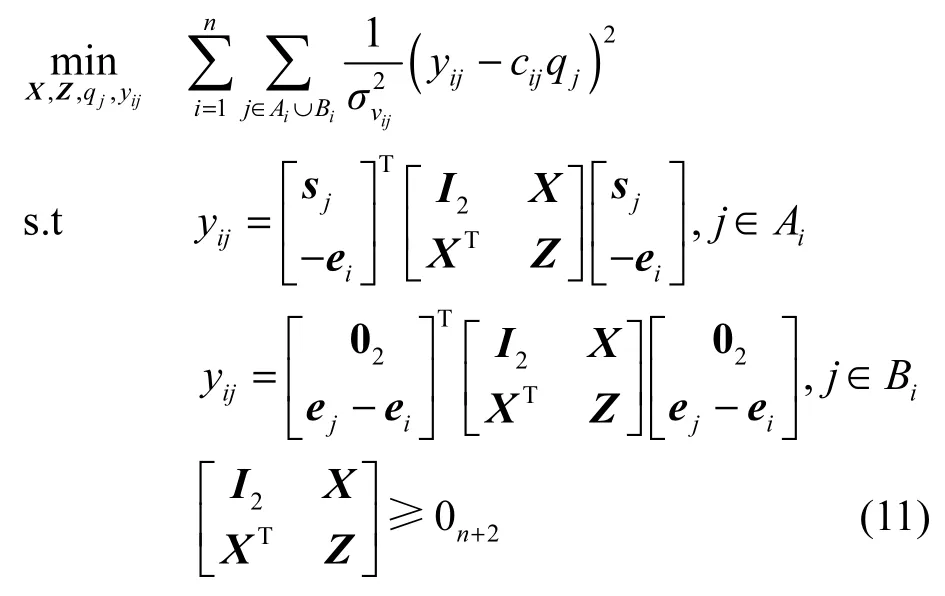
其中，ei表示一个m×1的向量，它的第i个元素为1，其他的元素都为0。当式(11)的目标函数取得最小值时，即存在X和Z，可以使Z=XTX成立，则式(11)和式(10)的解是一致的。式(9)和式(11)所描述的半定规划问题可以通过很多已知的算法很容易地求出对应的最优解，如内点法。在Matlab仿真中，可以采用标准的SDP解析工具SeDuMi或SDPT3直接求解对应的SDP问题。

4 计算复杂度分析

基于浮点数计算的总数或每秒浮点计算评估RSRSL算法的计算复杂度，并和ML、LLS、LMdS、投票法的计算复杂度进行对比。假设在实数域中，每个加减乘除操作以及平方根操作可以通过一次浮点计算完成。推导RSRSL算法在多目标网络中的计算复杂度，单目标网络是多目标网络在n=1时的特殊情况。其中，n表示网络中普通节点的总数；m表示信标节点的总数；表示网络的连通数。当传感网络是全连通图时，。对于一个标准的半定规划问题，目标函数中包括一个向量和m+1个对称矩阵。可以采用如内点法之类的迭代优化算法进行求解，对于每次迭代过程，最坏的情况下，求出半定规划最优解的计算复杂度是。根据求解的精度要求，迭代的次数为，其中，ς表示求解半定规划优化解需要达到的精度。针对RSRSL算法，只考虑算法中占主导地位的计算元素，。RSRSL算法的计算复杂度为。当传感网络是全连通图时，RSRSL算法和其他定位算法的计算复杂度如表1所示，其中，k表示迭代次数；m1表示网络中需要划分的子集数目；n1表示网络部署区域划分网格的数目。

表1 不同定位算法的计算复杂度（全连通网络）

接下来对比RSRSL算法与ML、LLS、LMdS和投票法的计算复杂度。对于ML算法，采用牛顿迭代法进行求解时，它的精度主要依赖于初始值的选取和需要的精度。LMdS算法需要将网络中的节点分成m1个子集，计算复杂度随恶意节点的增多而急剧变大。投票法的定位精度依赖于网络部署区域的网格大小，计算复杂度也与网络中网格的数量有关。网络部署区域越大，划分的网格越小，网格数量越多，计算复杂度越高。而从上述对RSRSL算法的计算复杂度分析可以看出，RSRSL算法与网络部署区域大小没有关系，与恶意节点的数目也没有关系。对于一个包含较多普通节点的密集网络，RSRSL算法和ML算法在每次迭代的计算复杂度是类似的，但是要大于LLS的计算复杂度。但是对于一个网络只包含较少普通节点的网络，如只有10个普通节点的网络，3种算法每次迭代的计算复杂度是近似相同的。

5 仿真和性能分析

为了验证RSRSL算法的定位性能,分别基于仿真实验和实测实验对RSRSL算法进行分析，并将其与已有的安全定位算法进行对比。采用均方根误差来表示定位误差：，其中，表示估算得出的普通节点坐标，表示普通节点的真实坐标。

5.1 仿真实验

在一个60 m×60 m的矩形区域随机部署30个信标节点和50个普通节点，每个节点的通信半径为100 m。在一台处理器为Intel Core i5-4590，主频3.3 GHz，内存16 GB，1 600 MHz DDR3的台式机上对所有算法进行仿真，对每一种算法进行1 000次仿真实验。对于LMdS算法，设置子集的数量m1=20，每个子集中节点的个数n=4。对于投票法，设置网格的大小为1 m×1 m，即n1=60。利用CVX工具箱中的SeDuMi解析器对RSRSL算法进行求解。

图1所示为不同攻击强度下各种定位算法的定位性能。图1（a）表示有20%的信标节点遭受恶意攻击，发射信号强度被恶意篡改后，测量噪声标准差和定位精度之间的关系。从图中可以看出，当攻击强度较低时，LLS的定位误差最大，而且定位误差随着测量噪声的增加急剧变大。RSRSL算法和LMdS算法、投票法的定位误差较小，具有相似的定位性能，而且3种算法的定位误差不会随着测量噪声的增加发生大的波动。图1（b）表示有50%的信标节点遭受攻击时，测量噪声标准差和定位精度之间的关系。当网络中的恶意攻击节点增多时，LMdS算法会导致严重的定位误差，但是RSRSL算法仍能表现出较好的定位性能，因为RSRSL算法将发射功率看成一个未知变量参与定位计算，可以有效地缓减恶意节点篡改发射功率对定位的影响。投票法也表现了很好的定位性能，由于网格点的不连续性，它的定位误差要略微高于RSRSL算法，而且投票法的定位精度受到网格大小的影响，当将网格划分的更小时，会带来较低的定位误差，但是会带来巨大的计算复杂度，并需要很高的内存空间。

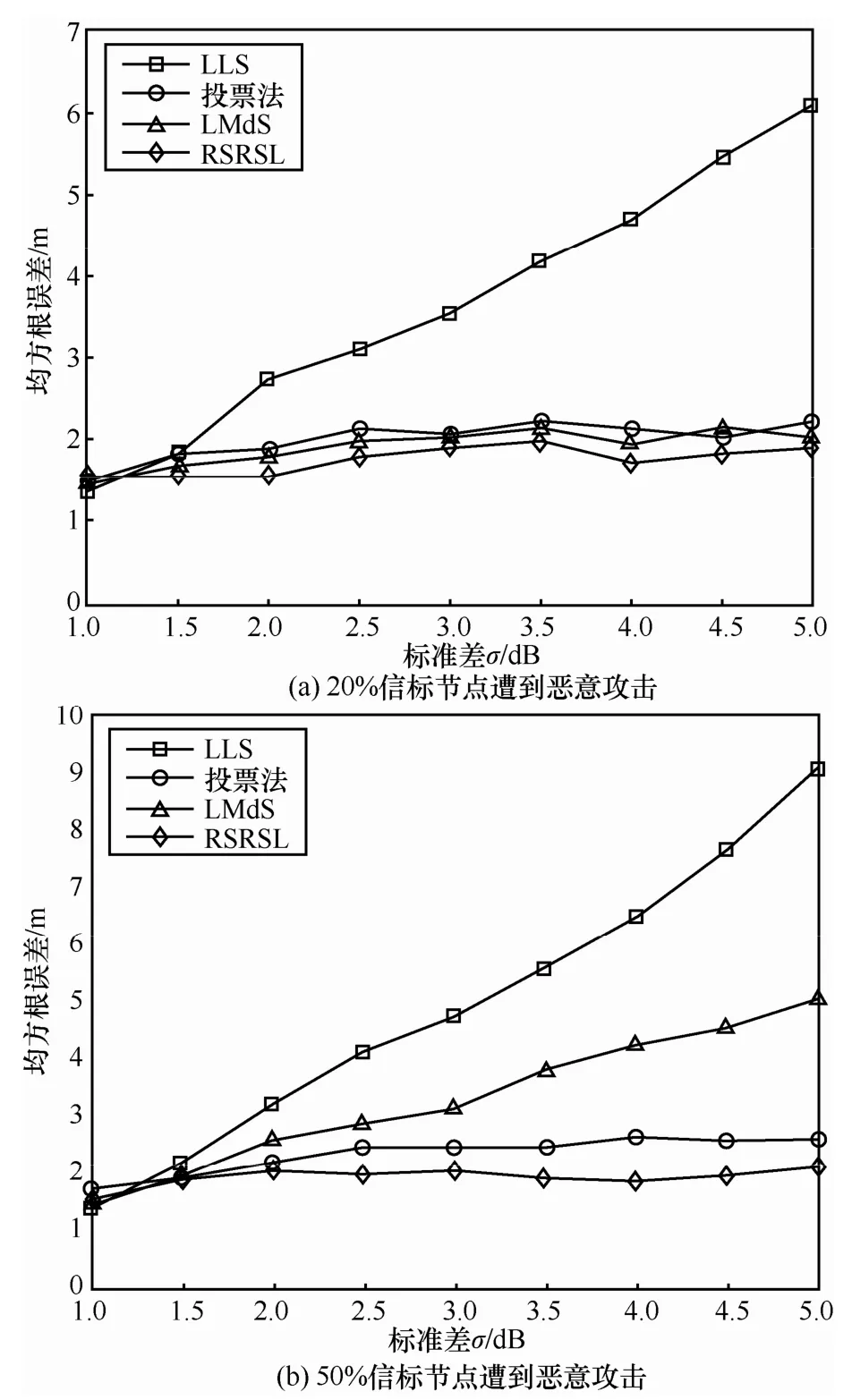
图1 不同攻击强度下各种算法的定位误差

图2所示为不同攻击强度下，噪声标准差σ=3dB时不同算法准确估算出正确位置的概率。由于存在测量噪声和有限的网格大小，本文设定当估算位置在真实位置的αm范围内时，即认为算法收敛到正确位置。当恶意信标节点的数量小于50%时，除了LLS算法，其他的安全定位算法都有较好的定位性能，有 90%的概率使估算的位置收敛于正确位置。当恶意信标节点的数量大于50%时，所有的定位算法的定位性能都降低，但RSRSL算法明显优于其他算法。如当恶意信标节点的数量为60%或70%时，RSRSL算法收敛于正确位置的概率要比其他算法高10%左右。

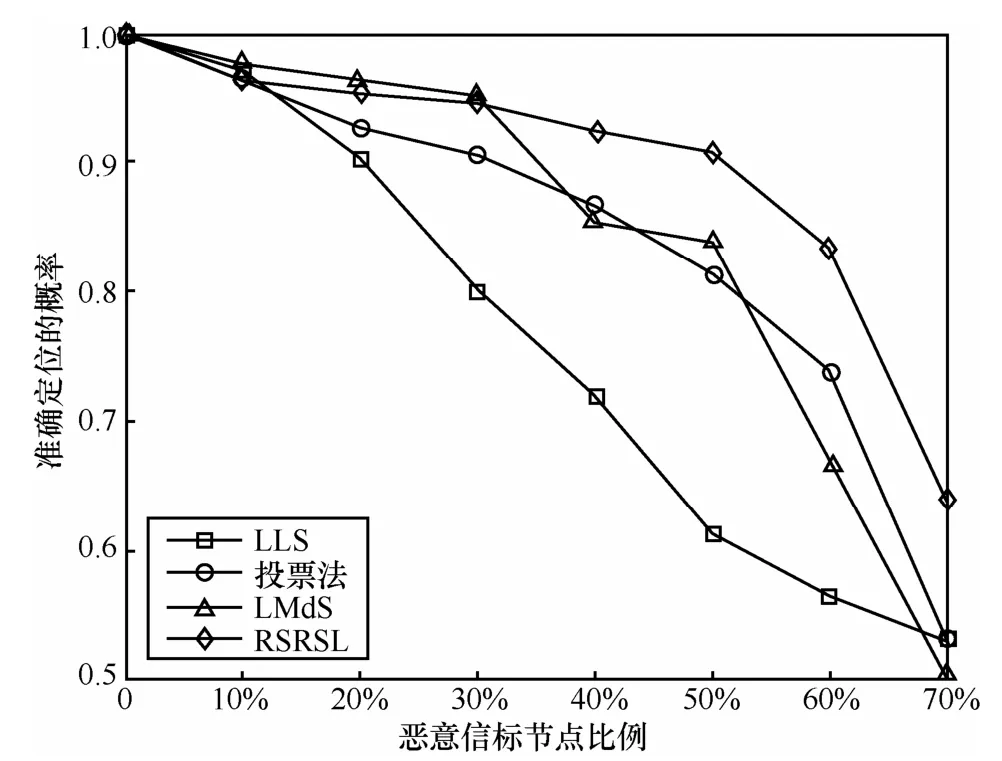
图2 不同攻击强度下各种算法准确定位的概率

图3所示为当有20%的信标节点遭受恶意攻击时，普通节点的邻居节点数目对定位误差的影响。从图中可以看出，当邻居节点的数量慢慢变大时，即网络的连通度增大时，所有算法的定位性能都得到了显著的提高。当普通节点周围的邻居节点较少时，LLS和ML算法具有较高的定位误差，其中，LLS的定位误差最大，RSRSL算法的定位性要远远优于LLS和ML算法。虽然随着邻居节点的增加，LLS和ML的定位误差有了显著的降低，但是RSRSL算法仍然要明显优于ML和LLS算法。

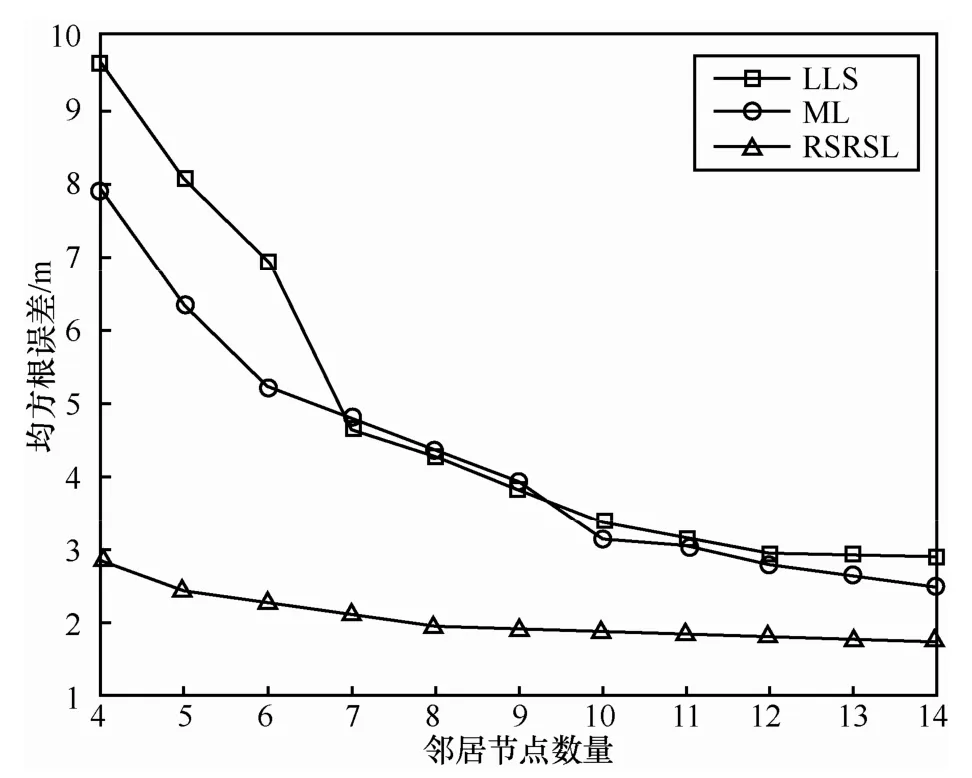
图3 邻居节点数对定位误差的影响

5.2 实测实验

在湖南大学电气学院的实验室对RSRSL算法进行验证，实测环境是一个6.4 m×4.2 m的实验室，室内有桌子、椅子和电脑等设施，在室内部署了12个信标节点、5个普通节点和1个中心节点，中心节点通过串口和上位机连接。每个节点都基于CC2430芯片，天线都是波长的全向天线，所有节点通过ZigBee协议组成一个传感网络，每个节点的有效通信半径为10 m。通过调整信标节点的发射功率大小或设置障碍物来模拟恶意攻击环境。在进行实验之前，利用训练测试数据提前计算出当前环境中的路径衰减系数，设计了100组实验来验证RSRSL算法的定位精度。

图4描述了在有20%的信标节点遭受恶意攻击时，不同算法定位误差随测量噪声标准差变化的情况。图4(a)和图4(b)分别表示网络中有1个普通节点和5个普通节点时的定位性能。虽然网络中部署的普通节点数目不同，但所有算法的定位性能都受测量噪声标准差的影响，定位误差随着测量噪声的增大而提高。其中，LLS算法受测量噪声变化的影响是最大的，而且随着测量噪声的逐渐增大，定位误差的变化越来越大。和仿真实验相比，实测实验中所有算法的定位性能要稍微弱于仿真的定位性能，这是因为在实测实验中RSSI会受到多径效应以及室内其他无线信号的影响。但是和仿真实验的结果类似，RSRSL算法的定位性能在实测环境中也要明显优于传统的定位算法。

图4 存在20%恶意信标节点下不同算法的定位误差

6 结束语

在攻击环境中，如何准确、安全地确定WSN节点的位置是目前的研究热点。针对重放、伪造插入等外部攻击会恶意篡改信标节点发射功率的问题，提出了一种新的无需过滤恶意信标节点的安全定位算法RSRSL。该算法考虑发射功率会被恶意篡改，不仅利用信标节点的RSSI测量值，而且利用普通节点的RSSI测量值建立了对应的安全定位模型。通过将非线性的定位问题转化为半定规划问题估算出普通节点的位置，并在数学上分析了RSRSL算法的计算复杂度。仿真和实测实验表明，在存在攻击的环境中，RSRSL算法能够实现安全定位，定位性能要明显优于已有的定位算法。

[1]CAN Z,DEMIRBAS M.A survey on in-network querying and tracking services for wireless sensor networks[J].Ad Hoc Networks,2013,11(1):596-610.

[2]ZHAO J,XI W,HE Y,et al.Localization of wireless sensor networks in the wild:pursuit of ranging quality[J].IEEE/ACM Transactions on Networking (TON),2013,21(1):311-323.

[3]HUANG J,XUE Y,YANG L.An efficient closed-form solution for joint synchronization and localization using TOA[J].Future Generation Computer Systems,2013,29(3):776-781.

[4]GHOLAMI M R,GEZICI S,STROM E G.TDOA based positioning in the presence of unknown clock skew[J].IEEE Transactions on Communications,2013,61(6):2522-2534.

[5]MALAJNER M,PLANINSIC P,GLEICH D.Angle of arrival estimation using RSSI and omnidirectional rotatable antennas[J].Sensors Journal,IEEE,2012,12(6):1950-1957.

[6]SAHU P K,WU E H K,SAHOO J.DuRT:dual RSSI trend based localization for wireless sensor networks[J].Sensors Journal,IEEE,2013,13(8):3115-3123.

[7]JIANG J A,ZHENG X Y,CHEN Y F,et al.A distributed RSS-based localization using a dynamic circle expanding mechanism[J].Sensors Journal,IEEE,2013,13(10):3754-3766.

[8]ZEYTINCI M B,SARI V,HARMANCI F K,et al.Location estimation using RSS measurements with unknown path loss exponents[J].EURASIP Journal on Wireless Communications and Networking,2013(1):1-14.

[9]SO H C,LIN L.Linear least squares approach for accurate received signal strength based source localization[J].IEEE Transactions on Signal Processing,2011,59(8):4035-4040.

[10]WANG C,QI F,SHI G,et al.A linear combination-based weighted least square approach for target localization with noisy range measurements[J].Signal Processing,2014,94:202-211.

[11]WEI Y,GUAN Y.Lightweight location verification algorithms for wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(5):938-950.

[12]HE D,CUI L,HUANG H,et al.Design and verification of enhanced secure localization scheme in wireless sensor networks[J].IEEE Transactions on Parallel and Distributed Systems,2009,20(7):1050-1058.

[13]LI Z,TRAPPE W,ZHANG Y,et al.Robust statistical methods for securing wireless localization in sensor networks[C]//The 4th International Symposium on Information Processing in Sensor Networks.Los Angeles,USA,2005:91-98.

[14]LIU D,NING P,LIU A,et al.Attack-resistant location estimation in wireless sensor networks[J].ACM Transactions on Information and System Security,2008,11(4):1-39.

[15]GARG R,VARNA A L,WU M.An efficient gradient descent approach to secure localization in resource constrained wireless sensor networks[J].IEEE Transactions on Information Forensics and Security,2012,7(2):717-730.

[16]ZHONG S,JADLIWALA M,UPADHYAYA S,et al.Towards a theory of robust localization against malicious beacon nodes[C]//The 27th Conference on Computer Communications.Phoenix,USA,2008:1391-1399.

[17]詹杰,刘宏立 ,刘大为,等.无线传感器网络中DPC安全定位算法研究[J].通信学报,2011,32(12):8-17.ZHAN J,LIU H L,LIU D W,et al.Research on secure DPC localization algorithm of WSN[J].Journal on Communications,2011,32(12):8-17.

徐琨（1979-），男，湖南常德人，湖南大学博士生，主要研究方向为无线传感器网络定位与追踪、移动互联等。

刘宏立（1963-），男，湖南常德人，湖南大学教授、博士生导师，主要研究方向为无线传感器网络、移动通信系统、软件无线电、智能信息处理与传输技术等。

詹杰（1973-），男，湖南常德人，博士，湖南科技大学副教授，主要研究方向为无线传感网络定位、移动通信等。

马子骥（1978-），男，湖南长沙人，博士，湖南大学讲师，主要研究方向为下一代智能通信网络、数字信号处理等。

Malicious attack-resistant secure localization algorithm for wireless sensor network

XU Kun1,LIU Hong-li1,ZHAN Jie2,MA Zi-ji1
(1.College of Electrical and Information Engineering,Hunan University,Changsha 410082,China;2.College of Physics and Electronic Science,Hunan University of Science and Technology,Xiangtan 411201,China)

In hostile environments,localization often suffers from malicious attacks that may distort transmit power and degrade positioning accuracy significantly for wireless sensor network.A robust semidefinite relaxation secure localization algorithm RSRSL was proposed to improve the location accuracy against malicious attacks.On the assumption of unknown transmit power,which is undoubtedly approximate to the fact of WSN,a novel secure location probability model was introduced for single-target and multi-target sensor networks,respectively.Taking the computational complexity of RSRSL into account,the nonlinear and non-convex optimization problem was simplified into a semidefinite programming problem.According to the results from both simulations and field experiments,it is clearly demonstrated that the proposed RSRSL has better performance on location accuracy,in contrast to the conventional localization algorithms.

wireless sensor network,security localization,

signal strength indicator,transmit power,semidefinite programming

s:The National Natural Science Foundation of China(No.61172089),The Central State-owned Capital Management and Budget Project of China (No.[2013]470),The National Doctoral Fund of China(2014M562100),The Science and Technology Program Foundation of Hunan Province(No.2014WK3001)

TP393

A

10.11959/j.issn.1000-436x.2016276

2016-07-29；

2016-11-21

国家自然科学面上基金资助项目（No.61172089）；中央国有资本经营预算支出基金资助项目（No.[2013]470）；博士后面上基金资助项目（No.2014M562100）；湖南省科技厅基金资助项目（No.2014WK3001）