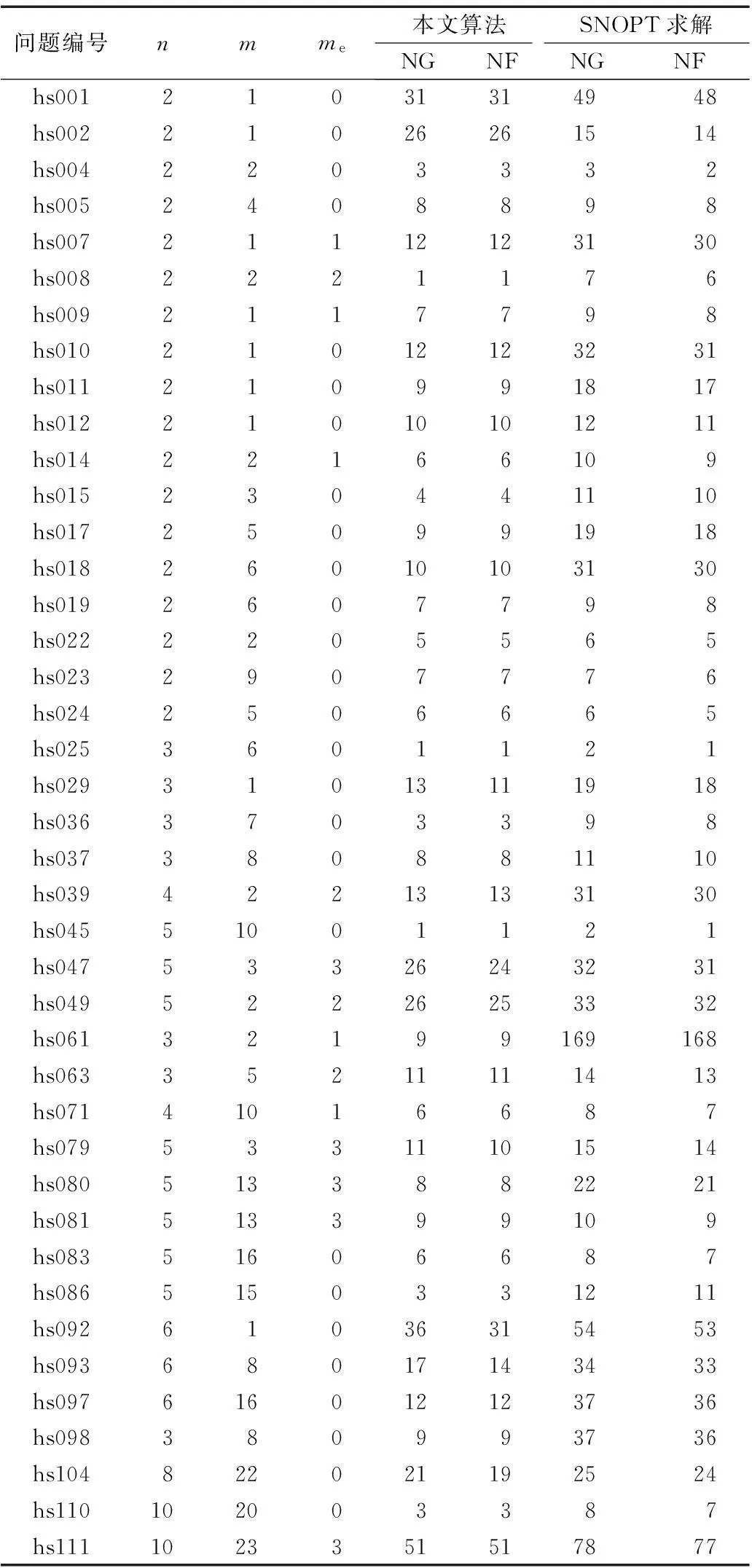
新的无罚函数无滤子的序列二次规划方法

王　波, 濮定国

(1.同济大学 数学系，上海 200092； 2.南京财经大学 应用数学学院，江苏 南京 210023)



新的无罚函数无滤子的序列二次规划方法

王波1,2, 濮定国1

(1.同济大学 数学系，上海 200092； 2.南京财经大学 应用数学学院，江苏 南京 210023)

摘要：对一般的具有等式约束和不等式约束的非线性规划问题，提出了一个无罚函数无滤子的信赖域序列二次规划算法.整个算法分为两个阶段，第一阶段计算可行步，以达到减少约束违反度的目的，第二阶段为优化阶段，以减少目标函数的二次模型为目的.此算法中可行步和优化步是相对独立的，任何减少约束违反度的算法都可以应用，具有更大的灵活性.在合理的假设条件下，证明了算法的全局收敛性和局部收敛性.通过数值实验证实了算法的有效性.

关键词：序列二次规划; 滤子; 罚函数; 非线性规划

(1)

其中x∈Rn,E={i|i=1,2,…,me},I={i|i=me+1,…,m},且f:Rn→R和c:Rn→Rm是光滑函数.式(1)的拉格朗日函数为

(2)

其中λ∈Rme和μ∈Rm-me是乘子.式(1)的Karush-Kuhn-Tucker条件(KKT条件)为

cE(x)=0

cI(x)≤0

(3)

满足KKT条件的点称为KKT点.

一个非线性规划问题必须处理或者可能面对两种不同的迭代, 分别是优化和可行性.优化是通过目标函数f(x)度量的，即使目标函数下降；可行性一般是通过约束违反度度量的, 例如,h定义为

(4)

其中‖·‖是一个任意范数，且[c(x)]+∶=max{c(x),0}.

算法中目标函数和约束违反度这两个准则必须都得到优化，算法就是在每一步迭代中让这两个准则的优化得到平衡.一些非线性规划的算法采用价值函数作为工具，使目标函数和约束违反度两个准则的优化达到平衡，并且保证全局收敛性[1-2].

相对于价值函数方法, Fletcher等[3]介绍了一种滤子序列二次规划方法， 这是一种新的非线性规划全局方法的策略，数值结果显示，这种序列二次规划算法是非常有效的.Fletcher等[4]证明了滤子序列二次规划算法的全局收敛性.之后,很多全局收敛的滤子算法被提出.

近来，Gould等[5]介绍了一种新的解非线性等式约束优化的方法，在这种方法里，不用罚函数，滤子等.Yamashita等[6]也提出了一种对于具有非线性等式和非负约束的优化问题的无罚函数无滤子序列二次规划算法.Liu等[7]对非线性等式约束优化问题，提出了一种不用罚函数和滤子的序列二次规划算法.在此方法中，每一步的迭代的步长通过使目标函数值或者约束违反度充分下降得到.

本文提出了一种新的不用罚函数和滤子的序列二次规划算法.此序列二次规划方法中计算全步长分为两个阶段.首先, 计算可行步，目标是减少不可行测度h, 使步长满足线性化的约束条件.其次，优化阶段是为了在线性化的可行集里计算一个试探点，以减少目标函数的二次模型为目的.这种无罚函数无滤子的序列二次规划算法有几个优点：① 此算法对一般的具有等式约束和不等式约束的非线性规划问题适用；② 可行步和优化步是相对独立的，任何减少约束违反度h的算法都可以应用；③不需要估计罚参数，避免了罚参数选取过大或过小的问题.④ 试探步受到之前迭代例如滤子的影响较小.

1算法描述

设xk为当前迭代点，信赖域半径为Δ>0，通过求解如下二次规划:

(5)

计算步长，其中

(6)

Bk是正定对称阵, 且

(7)

可行步nk必须满足式(5)的约束限制并且nk的目标是减少不可行测度h，令

其中向量PL(xk)是xk在L(xk)上的投影.然而本文不采用这种特殊的选择，可以采用Martinez[8]的方法得到, 但是为了确保此阶段的有效性，给出如下合理的假设(参见文献[9]).

假设1存在常数δh>0和cn>0使得对于所有满足h(xk)≤δh的k≥0，有

称式(5)是相容的，当L(xk)≠∅且‖nk‖≤ξΔ,其中ξ∈(0,1)是一个常数.

若式(5)是相容的, 当执行一个优化步tk时，期望模型产生一个满意的下降.设优化步tk是如下二次规划的估计解：

(8)

若式(5)是不相容的, 算法执行重启算法,重启算法的目的是为了获得xk+1，使h(xk+1)

(9)

(10)

具体算法如下

初始化:k=0,x0,0<Δmin<Δmax,Δ∈[Δmin,Δmax],γ,σ,β,λ1∈(0,1),λ2>1.

第1步:若满足式(1)的KKT条件，即式(3)满足，则终止算法.

第3步: 若L(xk)=∅, 利用重启策略得到xk+1.

第4步: 计算可行步nk使xk+nk∈L(xk),若‖nk‖>ξΔ,利用重启策略得到xk+1.

第6步: 若不等式

(11)

和

(12)

成立或者不等式

(13)

否则，Δ=max{λ1Δ,Δmin}并跳转第5步.

第7步: 利用阻尼的Broyden-Fletcher-Goldfarb-Shanno公式(BFGS公式)升级Bk+1.

第8步: 令k←k+1，并返回第1步.

注: 若试探步dk满足f(xk)-f(xk+dk)>σΔq且Δq>0,称此时的迭代为f-型迭代，若试探步dk满足Δq<0,称此时的迭代为h-型迭代.

2全局收敛性

在证明算法的全局收敛性之前，先给一些基本的假设.

H1 序列xk包含在凸闭紧集X⊂Rn中.

H2 所有的函数f(x),cE(x),cI(x)是二次连续可微的.

H3 Hesse阵的估计阵{Bk}是上有界的且存在常数M>0使得对于所有的k,有

(14)

引理2设假设H1和H2成立，则存在常数ch>0，使对所有的xk∈X和Δ>0，由算法得到的dk满足

(15)

证明该结论可以直接由文献[12]的引理3.2得到.

引理3设f(xk)是单调递减的并且下有界的，且h(xk)≥0.若对所有的k,

(16)

成立，则h(xk)→0.

证明该结论可以直接由文献[4]的引理1得到.

引理4设无限迭代序列{xk}为h-型迭代并满足{h(xk)}>0，f(xk)是下有界的，则{h(xk)}→0.

证明该结论可以直接由文献[10]的引理3得到.

引理5若d是式(5)的可行点, 则有

(17)

和

(18)

证明该结论可以直接由文献[4]的引理4得到.

引理6设x*∈X是式(1)的可行点，并且在此点处MFCQ(Mangasarian-Fromovitz 约束规范)条件满足, 但不是KKT点，则存在x*的一个邻域N*，正数ε,μ和κ，对所有的xk∈N*∩X和Δ，其中Δ满足

(19)

式(1)有一个可行解d，在此点处的预测减少满足

(20)

并且

(21)

成立，及

(22)

证明此结论直接由文献[4]的引理5得到.

引理8内循环是有限终止的，即内循环经过有限步迭代终止.

证明该结论可以直接由文献[10]的引理7得到.

定理1假设H1～H4成立, 由算法生成的序列会满足以下两种情形之一：

(A) 式(1)的KKT点被得到.

(B) 存在序列的一个可行聚点，此聚点或者是KKT点，或者不满足MFCQ条件.

证明下面证明存在一个聚点或者是KKT点或者不满足MFCQ条件.考虑两种情况.

第一种情况, 考虑主序列中包含无限个使Hk升级的迭代点，记这样的迭代点所形成的子序列为S.由引理4, 在S中，有

(23)

因此

(24)

因为所有的迭代点xk都位于X中, 而X是紧的, 因此迭代序列至少有一个聚点.因此，可以找到序列S的一个子序列S′，设x∞为子序列的一个可行聚点，并且S′中Hk被升级.

下面采用反证法，假设在x∞处满足MFCQ 条件，但不是KKT点.由引理 6，存在x∞的一个邻域N∞，及ε,μ和κ>0，使得，若μh(xk)≤Δ≤κ满足，则d为式(5)的可行解，并满足式(21)和式(22).

(25)

则f-迭代的所有条件都满足.下面说明将会产生f-迭代.

(26)

当k充分大时，式(25)的下界是式(25)上界的二阶无穷小.在内循环中，信赖域半径Δ的连续减少使得信赖域半径最终落到式(25)的区间内, 或者落到该区间的右侧.当信赖域半径Δ落入式(25)的区间内时，则必产生f-迭代.

当信赖域半径Δ的连续减少使得信赖域半径最终落到式(25)的区间右侧时，因为d是式(5)的全局最小值, 当Δ减少时，Δq单调递减，Δq>0可能会由成立变为不成立，但是反之不会成立.因此, 内循环通常在一个h-迭代之前可能会有f-迭代，且对任意的Δ≥μh(xk)，不会产生h-迭代.

因此，在此子序列中产生一个f-迭代， 这与此序列中点都是h-迭代组成的矛盾.所以x∞或者是KKT点或者不满足MFCQ条件.因此情况(B)成立.

第二种情况, 考虑主序列中仅有有限步的h-迭代.存在正数K，使得对所有的k>K，都是f-迭代.由引理3得h(xk)→0. 因此序列的任何聚点x∞都是可行点.

类似于第一种情形,假设在点x∞处MFCQ条件满足但不是KKT点.由引理6和引理7, 存在x∞点的一个邻域N∞及ε,μ,κ>0，使得，若

(27)

式(5)是相容的 并且相应的试探步d满足f-迭代的条件和式(20)，(21).

因为对于所有的k>K的迭代都是f-迭代, 即Hk从第K步迭代以后就不再改变.因此，k>K,Hk中第二大元素Hk2是常数，这时式(27)的右边为常数, 与k无关, 而式(27)的左边收敛到0.因此，当k充分大时

在这种情形下, 当Δ在内循环减少时, 它最终必须落到式(27)的区间内或者落到式(27)的区间右侧.因为在每一步内迭代中Δ每次减少λ倍，并且对于任意的Δ在式(27)的区间内，则产生f-迭代.因此，选择Δ满足

(28)

这时f-迭代产生.因此，由式(20)，(21)和(28)得

对于所有充分大的k成立, 这与{f(xk)}是有下界的矛盾.因此，x∞是一个KKT点，在这种情形下，情况(B)成立.

3数值结果

本节将算法给出的数值结果列于表1中，所有的测试问题来自文献[13]中的问题. 问题的编号与文献[13]中的相同.通过比较本文算法和SNOPT(5.3版)的数值结果来证明算法的有效性.SNOPT求解器是目前最流行的求解大规模非线性规划的软件之一，它本身也是一类采用价值函数的拟Newton型序列二次规划方法.表1中NF为目标函数和约束函数的计算次数;NG为梯度的计算次数;n表示问题中变量的维数;m表示问题中约束的维数;me表示问题中等式约束的维数.运算过程中, B0=I,正定矩阵Bk由阻尼的BFGS方法更新.

表1　数值结果

其中参数选择如下:γ=10-4,β=1-10-4,σ=0.1,λ1=0.5,λ2=2,ε=10-6,Δ=10,Δmin=10-4,Δmax=100,kH=104，l=3.

数值结果表明, 本文算法的数值结果比SNOPT求解的数值结果好.无罚函数无滤子的序列二次规划方法的步伐接受机制是有效的.

参考文献:

[1]Gomes F A M, Maciel M C, Martinez J M. Nonlinear programming algorithms using trust regions and augmented Lagrangians with nonmonotone penalty parameters[J]. Math Program, 1999, 84(1):161.

[2]Han S P. A globally convergent method for nonlinear programming[J]. Journal of Optimization Theory and Applications, 1977, 22(3):297.

[3]Fletcher R, Leyffer S. Nonlinear programming without a penalty function[J]. Mathematical Programming, 2002, 91(2):239.

[4]Fletcher R, Leyffer S, Toint P L. On the global convergence of a filter-SQP algorithm[J]. SIAM Journal on Optimization, 2002, 13(1): 44.

[5]Gould N I M, Toint Ph L. Nonlinear programming without a penalty function and a filter[J]. J Comput Math, 2010, 122(1):155.

[6]Yamashita H, Yabe H. A globally convergent trust-region SQP method without a penalty function for nonlinearly constrained optimization[R]. Tokyo: Mathematical Systems Inc, 2003.

[7]Liu X, Yuan Y. A sequential quadratic programming method without a penalty function and a filter for equality constrained nonlinear programming[J]. SIAM J on Optimization, 2011, 21(2):545.

[8]Martinez J M. Inexact-restoration method with Lagrangian tangent decrease and a new merit function for nonlinear programming[J]. J Optim Theory Appl, 2001, 111(1):39.

[9]Martinez J M. Two-phase model algorithm with global convergence for nonlinear programming[J]. Journal of Optimization Theory and Applications, 1998, 96(2): 397.

[10]Huang M X, Pu D G. A trust region SQP method without a penalty or a filter for nonlinear programming[J]. Journal of computational and applied mathematics, 2015, 281(1):107.

[11]Zhu X J, Pu D G. A new double trust regions SQP method without a penalty function or a filter[J]. Computational Applied Mathematics, 2012, 31(2): 407.

[12]Ribeiro A A, Karas W K, Gonzaga C C. Global convergence of filter methods for nonlinear programming[J]. SIAM Journal on Optimization, 2008, 19(2): 1231.

[13]Hock W, Schittkowski K. Test examples for nonlinear programming codes[M]. Berlin, Heidelberg, New York: Springer-Verlag, 1981.

考虑如下非线性规划问题:

A New Sequential Quadratic Programming Method Without a Penalty Function or a Filter

WANG Bo1,2, PU Dingguo1

(1. Department of Mathematics, Tongji University, Shanghai 200092, China; 2. School of Mathematics, Nanjing University of Finance and Economics, Nanjing 210023, China)

Abstract：A sequential quadratic programming method without using a penalty function or a filter was proposed. The algorithm computes the overall step in two phases. The first phase is to compute a feasibility step. The feasibility phase aims at reducing the infeasibility measure. The second phase, an optimality phase computes a trial point reducing a quadratic model of the objective function. The feasibility and optimality phases are independent in this algorithm; therefore, any method for reducing constraint violation can be used in the feasibility phase. Under mild conditions, the method can be proved to be globally convergent. Numerical results demonstrate the efficiency of this algorithm.

Key words：sequential quadratic programming; filter; penalty function; nonlinear programming

收稿日期：2015-06-09

基金项目：国家自然科学基金(11371281,11201221);江苏省自然科学基金(BK2012468);江苏省高校自然科学基金(14KJD110003)

中图分类号：O221.2

文献标志码：A

第一作者： 王波(1979—)，男，副教授，博士生，主要研究方向为数学规划.E-mail: 1110468@tongji.edu.cn