聚合酶链式反应仪基座的热阻建模与分析

许秀锋， 周爱国， 殷俊锋， 刘　备

(1.同济大学 机械与能源工程学院，上海 201804； 2.同济大学 数学系，上海 200092)



聚合酶链式反应仪基座的热阻建模与分析

许秀锋1， 周爱国1， 殷俊锋2， 刘备1

(1.同济大学 机械与能源工程学院，上海 201804； 2.同济大学 数学系，上海 200092)

摘要：对聚合酶链式反应仪(PCR)基座中温度变化规律进行数学建模，求出其过程热阻值，并利用该热阻值对类似模型的温度场进行仿真计算，从而快速地得出考虑若干关键参数的复杂模型的温度场.计算结果显示,PCR仪基座的过程热阻与其自身的导热热阻存在某种关系，进而提出一个对于该关系的假设和数学描述，最后对该假设应用的可行性进行数值计算证明.

关键词：聚合酶链式反应； 温度场； 过程热阻

聚合酶链式反应仪(Polymerase Chain Reaction Instrument，PCR)作为分子生物学的基础仪器，其实验效果在很大程度上取决于基座温度的多梯度精确控制，而从半导体制冷器(thermoelectric cooler，TEC)传递至基座的热阻模型对温控效果具有决定性的作用.对于导热热阻以及等效导热系数，已有研究者进行过推导[1-2]，但没有对PCR基座的过程热阻进行研究.本文旨在考虑各方面因素计算试剂边界处的热阻值，利用集总热容法分析非稳态导热过程，并忽略物体内部的热阻，即热阻仅存在于边界处，对其进行一定的简化，并最终用于数值仿真.

1传热计算模型建立

聚合酶链式反应仪的整体模型如图1a所示[3-4].

a 多管整体模型b 单试管三维模型

图1PCR仪基座整体模型

Fig.1Model of the base of PCR instrument

进行传热分析时，整个基座的分析会显得十分复杂，可分解成图1b所示的小模块，每个模块的温度变化规律是相同的，传热模型如图2a所示.

图2a为小模块的整体传热模型，其热源为基座下方的半导体制冷器(thermal electrical ceramic，TEC)，其维持在一个固定的温度，并且在基座和TEC之间涂有导热物质，用以减少基座和TEC之间的接触热阻.

a 单试管传热模型b 试剂加热模型

图2单试管的传热模型图

Fig.2Heat-transfer model of single tube

2集总热容法计算的理论依据

所谓的集总热容法[5]就是指忽略物体内部的导热热阻，但这显然与本题中的模型是不同的，所以并不能直接将此方法运用于上述模型.

本文假设将基座内部的导热热阻全部集中于边界处，将基座内部大致看作是无热阻，如此基座和TEC之间就存在有一定的热阻，从而可以使用集总热容法.该假设的理论前提是，基座内部在某一时刻温度几乎相等，并且在动态边界条件下的响应速度也几乎相同.TEC与基座间传热模型如图3所示.

图3　基座部分正视图

铝制基座上表面以及中间和侧面孔表面均可视为绝热.根据已知条件可以列出其导热微分方程为

(1)

式中：t1为温度函数，自变量为距基座底部的高度x和时间τ；a为铝的热扩散系数，a=9.3×10-5m2·s-1.该方程的边界条件为

(2)

(3)

式中：tw为TEC温度值；d为基座总高度；λ为铝的导热系数，λ=238 W·(m·K)-1.

初始条件为

(4)

当tw=1 ℃，d=10 mm时，即在单位阶跃的边界条件下，基座的温度响应为

(5)

式中：m=0,1,2….

图4为基座在单位阶跃下的温度响应.对于阶跃温度响应，在基座的不同高度，其温度的变化规律几乎一样，但是由于在初始的某一时刻其不同高度处的温差还是比较明显，所以在这种情况下并不能将其视作使用集总热容法的有效依据.然而实际的加热为斜坡上升，故研究此种边界条件下的温度响应才能真正地反应其规律.

图4　基座在单位阶跃下的温度响应

Fig.4Temperature response under the unit step of the base

由杜哈美尔定理[5]可知，当边界温度为任意函数时，温度响应为

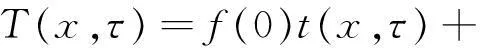
(6)

当f(η)为一斜坡函数时，df(η)/dη表示的是该斜坡的斜率，是一个常数，在这里设这个常数为C，则原函数可以写作

(7)

结合式(5)采取杜哈美尔法计算得到基座对于斜坡温度的响应为

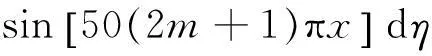
(8)

图5为基座在斜坡边界温度下的响应.从图5可看出，在5.5 mm及10.0 mm基座处的温差仅为0.2 °C，并且温度响应的延迟也非常小，为10-2s级.所以在这种情况下，可以将基座内部的温度看作是相同的，进而在计算基座的动态温度时可以使用集总热容法.

图5　基座在斜坡边界温度下的温度响应

Fig.5Temperature response under the temperature ramp of the base

3基座过程热阻的计算与简化

设基座的过程热阻为R，利用集总热容法，可知基座温度t1是一个只关于时间τ的函数.基座吸收的热量和温度的关系为

(9)

式中：ρ为铝制基座密度，ρ=2 790 kg·m-3；c为基座的比热容，c=917 J·(kg·K)-1；A为基座与TEC的接触面积.

从TEC传递的热量为

(10)

由于此处的热量值相等，故有

(11)

将TEC温度tw和基座响应温度t1带入，即可得

(12)

其中

(13)

所以

e-2 500a(2m+1)2π2(τ-η)·

(15)

由式(15)可以看出,热阻R也是一个关于时间τ的函数.由于此热阻R的值很小，所以绘制其倒数1/R的函数图像，如图6所示.

图6　以不同高度为基准求得的1/R的值

从图6中可见，过程热阻的倒数1/R基本保持为一个不变的值，并且这个值大概是基座自身导热热阻Rd倒数的2～3倍，所以可以推测，其过程热阻大概为

(16)

简化的具体取值应该视模型的具体情况而定，比如模型的厚度、面积以及导热性能等.

这种简化方法还有一个很重要的前提就是接触热阻要小到可以忽略不计.一般情况下表面光滑的金属直接接触时的接触热阻为10-4级，在机器中往往添有导热材料，所以在简化计算时的热阻要远小于此量级，达到10-7.

4理论检验

4.1利用集总热容法和简化过程热阻计算试剂温度

利用集总热容法可以列出基座和试剂的温度控制方程

(17)

(18)

式中：ρ1，ρ2分别为基座和试剂的密度；cp1，cp2分别为基座和试剂的比热容；V1，V2分别为基座和试剂的体积；A1，A2分别为TEC与基座的接触面积以及基座与试剂的接触面积；t1，t2分别为基座和试剂的温度；h为等效传热系数;b相当于TEC与基座之间的传热系数，其数值为基座过程热阻的倒数，这里取2λ/d.

由于在初始时基座和试剂的温度都为0 °C，且在试剂中温度没有突变，所以存在初始条件

(19)

可以设

(20)

最后计算得试剂的温度为[6]

(21)

其中λ1,λ2是特征方程(22)的解，即

λ2+(C1+C2+C3)λ+C1C2=0

(22)

(23)

利用这种方法求出的试剂在TEC为单位阶跃温度时的温度响应如图7所示.

图7　利用集总热容法求出试剂温度响应

Fig.7Temperature response of the reagent based on the lumped capacitance method

4.2利用温度场详细解析法求解试剂温度场

基座，试管和试剂之间的配合关系如图2a所示.其中试剂的加热模型如图2b所示.

该试管的材料是聚丙烯，为一中空柱形，底部是半径为2.5 mm的半球，其柱体部分内径为4.0 mm，外径为5.0 mm，试管部分沿半径方向厚度为0.5 mm.聚丙烯材料的物理性质为导热系数λ=0.225 W·(m·K)-1，比热容c=1 860 J·(kg·K)-1，密度ρ=910 kg·m-3.液柱高度约3.0 mm.试剂的物理性质与水大体一致.

在传热过程中，热量是经过铝座、试管之后才传至试剂的.同时由于铝制基座的热扩散系数非常高，而且经由上面的分析可以看出，基座的温度可以很快地跟随TEC的控制温度，所以在这里可以将基座近似看作是热源.

虽然试剂和试管的接触面有两个面，但是热量是从侧面往中间传递，同时聚丙烯的导热能力要小于水，所以试剂与外界有热量交换的面可以看作是只有侧面一个面.根据这样的条件就可以认为试剂的温度场分布仅与半径r和时间τ有关，是一个二维温度场[7].

圆柱体的传热微分方程为[8]

(24)

该式的边界条件为

(25)

初始条件为

(26)

引入过余温度θ=T-T0，并采用分离变量法可得

(27)

式中:J0(x)为第一类零阶贝塞尔函数；μn为J0(x)的零点.

带入初始条件，可得

(28)

利用贝塞尔函数的性质[9]可得

(29)

式中：J1(x)为第一类一阶贝塞尔函数.

将式(29)带入至式(27)，可得

(30)

最后可以得到温度场的表达式为

(31)

由此可以求出试管内表面的温度响应，如图8所示.

由图8中可以看出,试管可以在很短的时间内上升至阶跃温度.同时以试管温度为边界温度，结合杜哈美尔定理，当边界温度为f(τ)时，试剂的温度为

(32)

图8　试管内表面温度响应

Fig.8Temperature response of the internal surface of the test tube

此处的Φ(r，τ)为圆柱在单位阶跃温度边界条件下的温度响应.结合式(31)可得

(33)

式中：r1为液柱的半径；a2为试剂的热扩散系数.

此处的边界温度f(τ)为

(34)

式中：r0为试管的外径；a1为试管的热扩散系数.

将式(33),(34)带入式(32)，可以得到

(35)

为计算方便，不妨设

(36)

可得

(38)

则有

(39)

将式(39)带入至式(35)，得

T(r,τ)=Φ(r,τ)-Δ(r,τ)=

(40)

按式(40)绘制时间-温度的变化曲线,如图9所示.

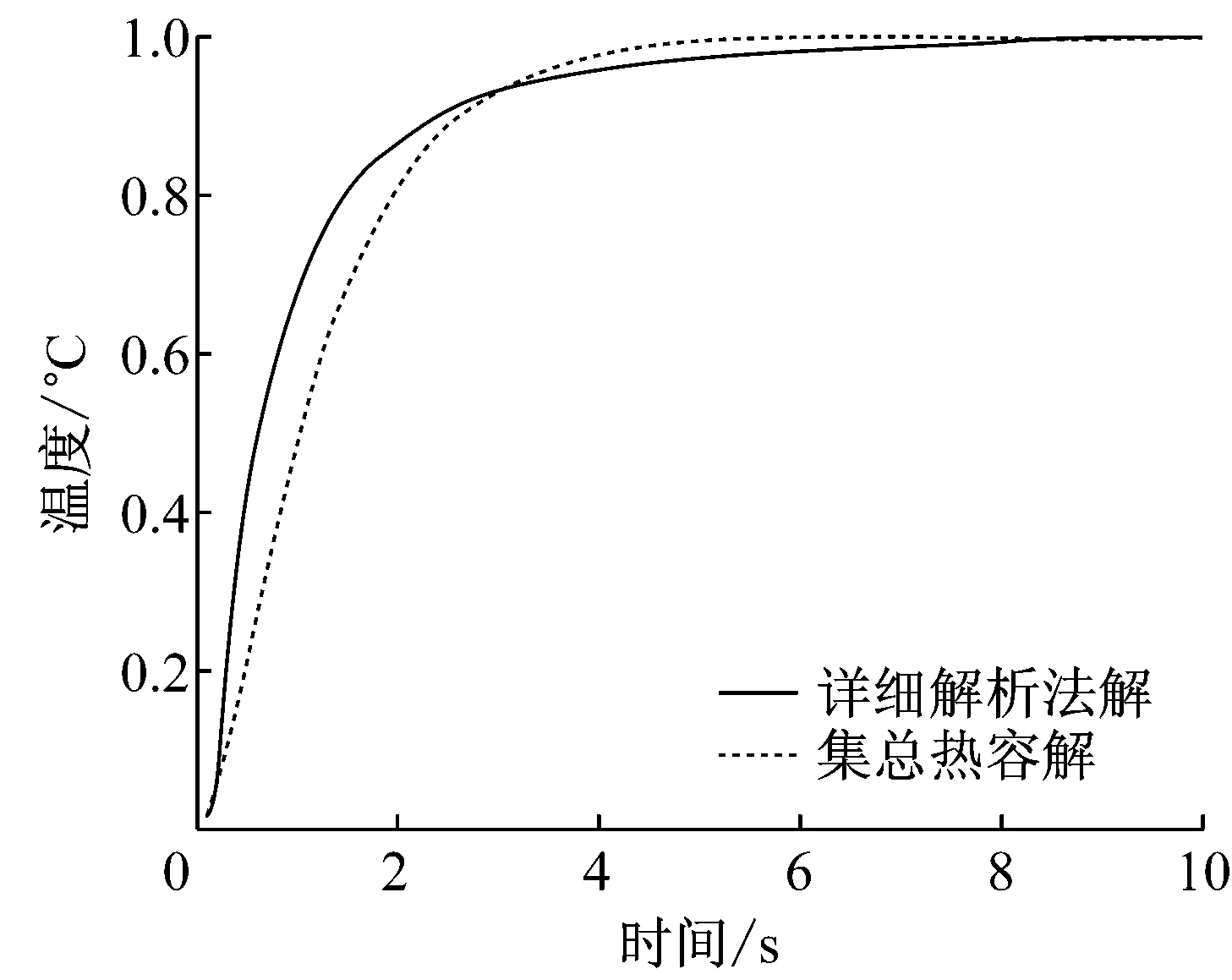
图9　详细解析解和集总热容解对比

Fig.9Comparison of the detailed analysis method and the lumped capacitance method

从图9中可以看出，利用集总热容法和简化后的过程热阻值计算出的试剂的温度曲线和利用常规解方法求出的试剂温度曲线非常相似，从整体上可以反映出其温度的变化规律.但是后者却比前者要复杂的多，计算繁琐，不利于实际工程的应用.

5结语

本文对PCR仪基座传热过程中的过程热阻值进行了计算，并且提出了与此热阻值有关的一种假设.该方法相当于对传统的集总热容法进行了一定的改进，当传热物体内部的温度变化大体一致时，可以视物体内部无热阻，在计算的时候只需考虑到边界处的热阻，同时还提出边界处的等效计算热阻值和其自身的导热热阻有一定关系.本文运用两种方法计算了试剂的温度场，可以看出，运用两种方法计算所得试剂的响应温度十分接近，同时也为该假设的可行性提供了理论依据.对比两种方法之后，可以发现集总热容法在计算时比温度场解析法简单方便很多.所以当某传热模型的传热过程比较复杂，但是符合使用该简化方法的条件时，使用集总热容法可以为温度场的计算提供很多的便利.

参考文献:

[1]张云斌，陆春林，金苏敏. 地板采暖地板层当量导热热阻的分析计算[J]. 流体机械，2006,5:74.

ZHANG Yunbin，LU Chunlin，JIN Sumin. Analysis and calculation for the floor surface effective thermal resistance of floor heating[J]. Fluid Machinery，2006,5:74.

[2]廖火生，刘小康，缪利梅. 热管等效导热系数的数值模拟[J]. 半导体光电，2013,5:795.

LIAO Huosheng，LIU Xiaokang，MIAO Limei. Numerical simulation on effective thermal conductivity of heat pipes[J]. Semiconductor Optoelectronics，2013,5:795.

[3]毛贺，陈章位，黄靖，等. PCR仪温度场热模型的研究与验证[J]. 浙江大学学报：工学版，2013，47(9):1619.

MAO He，CHEN Zhangwei，HUANG Jing，etal. Research and verification of thermal model for PCR instrument temperature field[J]. Journal of Zhejiang University：Engineering Science，2013，47(9):1619.

[4]何锐. PCR仪实验平台的热特性研究[D]. 上海：同济大学，2014.

HE Rui. Research on the thermal properties of PCR experiment platform[D]. Shanghai：Tongji University，2014.

[5]杨强生，浦保荣. 高等传热学[M]. 上海：上海交通大学出版社，1996.

YANG Qiangsheng，PU Baorong. Advanced heat transfer theory[M]. Shanghai：Shanghai Jiao Tong University Press，1996.

[6]李友荣. 高等传热学[M]. 北京：科学出版社，2013.

LI Yourong. Advanced heat transfer theory[M]. Beijing：Science Press，2013.

[7]比安什·A，福泰勒·Y，埃黛·J，等. 传热学[M]. 大连：大连理工大学出版社，2008.

Bianchi A，Fautrelle Y，Etay J，etal. Transferts thermiques[M]. Dalian：Dalian University of Science and Technology Press，2008.

[8]张善杰. 矢量分析、圆柱函数和球函数[M]. 南京：南京大学出版社，2011.

ZHANG Shanjie. Vector analysis, cylindrical function and spherical function[M]. Nanjing：Nanjing University Press，2011.

[9]闫桂峰，张琼，姜海燕. 数学物理方程与特殊函数[M]. 北京：电子工业出版社，2013.

YAN Guifeng，ZHANG Qiong，JIANG Haiyan. Mathematical physics equation and special function[M]. Beijing：Publishing House of Electronics Industry，2013.

Modeling and Analysis of Thermal Resistance of the Base of a PCR Instrument

XU Xiufeng1, ZHOU Aiguo1, YIN Junfeng2, LIU Bei1

(1. College of Mechanical Engineering, Tongji University, Shanghai 201804, China; 2. Department of Mathmatics, Tongji University, Shanghai 200092, China)

Abstract：Based on the mathematics modeling of the polymerase chain reaction(PCR) instrument basement, the value of process thermal resistance of the temperature variation law was obtained. Then, the process thermal resistance value obtained was used for the calculation of the the similar temperature field of key parameters, and the temperature field of a complex model was also easily solved even with some dedicated parameters. The simulation result show a relationship between the thermal resistance and the characteristic of the base of the PCR instrument. An assumption was proposed as well as a mathematics description. Finally, the feasibility of the application of this assumption is proved by numerical computation.

Key words：polymerase chain reaction; temperature field; thermal resistance

收稿日期：2015-10-20

通讯作者：周爱国(1973—)，男，副教授，主要研究方向为机电控制，生物仪器开发.E-mail：zhouaiguo@tongji.edu.cn

中图分类号：TK01

文献标志码：A

第一作者： 许秀锋(1977—)，男，博士生，主要研究方向为生物实验仪器建模与控制.E-mail：xuxiufeng@tongji.edu.cn