混合微分变换法在混凝土溶质运移问题中的应用

钟新然， 戴　瑛， 陈　熹

(同济大学 航空航天与力学学院，上海 200092)



混合微分变换法在混凝土溶质运移问题中的应用

钟新然， 戴瑛， 陈熹

(同济大学 航空航天与力学学院，上海 200092)

摘要：微分变换法是一种基于泰勒公式的求解方法，在求解包含间断条件的溶质运移偏微分方程(组)时会失效.采用将有限差分法与微分变换法相结合的求解思路，可使问题得到解决.利用该方法得到混凝土SO42-的反应性溶质运移方程以及CO2-SO42-和CO2-Cl-的全耦合溶质运移方程组的近似解表达式并将结果与有限元结果进行比较，证明了该方法的有效性.

关键词：混凝土； 溶质运移； 微分变换法； 有限差分法

混凝土是一种多孔介质，当它作为地下结构的材料时，土壤或地下水中的CO2,SO42-,Cl-等化学物质的侵蚀会导致混凝土力学性能劣化[1-4]，从而影响混凝土的承载力.因此，为了保证地下结构的使用安全，有必要对混凝土中的溶质运移过程进行分析.

1997年，Gospodinov等[4]通过相关实验标定SO42-的扩散系数，采用不稳定差分格式计算时间步长，获得二维硫酸盐溶质运移方程的数值解.2001年，窦红[5]将有限体积和有限元进行结合，求解非线性对流扩散问题并证明其数值解的稳定性.2009年，左晓宝等[6]对一维硫酸盐侵蚀混凝土的化学-力学(M-C)耦合方程进行Matlab自主编程，得到数值解.2012年，Bonakdar等[7]结合闭合形式的误差函数及有限元对氯离子扩散方程进行计算，分别获得考虑反应项为1阶以及2阶的近似解析解.

混凝土的溶质运移过程通常是由偏微分方程(组)描述的[4-7]，而微分变换法(differential transform method，DTM)是近20年发展起来的一种求解偏微分方程的方法，它由赵家奎于1986年首次提出[8]，此后， Arikoglu等[9]、 Özdemir等[10]、 Kangalgil等[11]和Shahed[12]等将其用于求解多种偏微分方程.在此，本文亦将其运用于求解混凝土中的溶质运移问题.

微分变换法是一种基于泰勒级数的求解方法，但在处理某些含间断条件的偏微分方程时，会出现级数的待定系数值不确定的问题，如混凝土溶质运移问题中初始条件间断时，级数的待定系数取值不唯一，从而使后续的求解无法进行.为解决该问题，本文利用Chu等[13]的混合微分变换法(hybrid differential transform and finite difference method, hybrid DTM and FDM)的求解思路，将问题在空间上按差分格式离散，在时间域上仍采用DTM进行求解，解决了间断条件导致的系数取值不确定问题.采用这种求解方法，得到混凝土SO42-的反应性溶质运移以及CO2-SO42-和CO2-Cl-的全耦合溶质运移方程的近似解表达式.

1微分变换法

微分变换法假设待求函数可展为泰勒级数形式，从而将原控制微分方程及初、边界条件转化为级数形式表示的方程，通过求解由各阶级数的待求系数构成的代数方程组，最终获得级数形式的近似解[8].

以一维溶质运移问题为例，设待求的化学物质质量浓度ρ(x,t)可以表示为[14]

(1)

式中：U(k,h)称为ρ(x,t)的微分变换函数，与ρ(x,t)有如下关系：

(2)

待求的原函数及其微分变换函数具有加法、乘积、微分等性质[14]，利用上述性质，可将控制微分方程以及初始、边界条件转化为关于U(k,h)的递推公式，求得U(k,h)的各项值并代入式(1)，即为ρ(x,t)的级数形式的近似解.

2含间断条件的溶质运移问题

一维溶质运移问题的控制方程具有如下形式[15]：

(3)

式中：D为扩散系数.

对于待求区域，在t=0时刻，x=0处，化学物质即将由此开始渗入，在x>0处,化学物质尚未到达，初始条件可写为

(4)

初始端及末端边界条件为

(5)

注意到式(4)的初始条件(含式(5)的边界条件)在x=0处是间断的.若用常规的DTM进行求解，设待求化学物质质量浓度ρ(x,t)仍可表示为式(1)的级数形式，且与U(k,h)满足式(2)的关系.将式(1)代入初始条件(4)，得到

(6)

而将式(1)代入边界条件式(5)后，得到

(7)

显然，当ρ0≠0时，由式(6)与式(7)可知，U(k,h)在k=h=0处的取值是矛盾的，因此，对于这种间断问题，常规的微分变换法是失效的.

3基于有限差分的微分变换法

为了解决上述初值点间断现象，本文采用混合微分变换法对混凝土溶质运移问题进行求解，其求解步骤如下[13,16-17]：

考虑一般情况下的控制微分方程

(8)

初始条件为式(4)，边界条件为式(5).

在空间沿x方向等分成n段，可得n+1个节点(含首末端).对域内每一个节点，都有

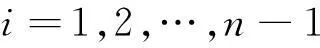
(9)

设域内两相邻节点的间距为Δx，则i点处的函数ρ(x,t)关于x的各微分项可由差分[18]获得

i=1,2,…,n-1

(10)

差分后的控制微分方程化为

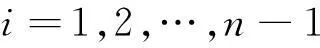
(11)

参照式(1),(2)的微分变换关系，在任意第i个节点上建立微分变换关系，有

(12)

(13)

将式(12)代入式(11)并结合微分变换的基本性质，可得关于微分变换函数Ui(k)的递推公式

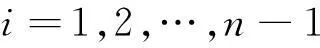
(14)

初始条件和边界条件相应地转化为

(15)

(16)

由式(15)和(16)可知，初始点间断问题不再影响到系数的取值.利用式(15)和(16)，以及Ui(k)的递推关系式(14)可以求得Ui(k)，将Ui(k)代入式(12)即可得到各节点处未知函数的近似表达式.

4数值算例

4.1SO42-反应性运移问题

SO42-在混凝土中反应性溶质运移方程[7]为

(17)

式中：ρS为SO42-质量浓度；D为扩散系数；R(ρS)为反应项，当R(ρS)仅取1阶反应项时[7]

(18)

式中：K为反应速率.

初始条件:

ρS|t=0=ρS,ini,x=0;ρS|t=0=0,x∈(0,L]

(19)

边界条件:

(20)

基本计算参数[7]为D=2×10-12m2·s-1，K=5×10-9s-1，L=0.05 m，ρS,ini=ρS,0=25 g·m-3.对域内划分节点见图1.

图1　节点划分(单位：m)

由式(11)可知，式(17)在空间点上有

i=1,2,…,9

(21)

其中ρS,i=ρS,i(t)，为在域内x=xi点的SO42-质量浓度值，在边界上，即i=0和10，ρS,i(t)的值可由边界条件确定.

由式(12),(13)可知，ρS,i(t)及其微分变换函数Wi(k)可以表示为

(22)

根据式(21)，利用原函数与微分变换函数的基本性质，可得微分变换函数Wi(k)满足

(k+1)Wi(k+1)=

(23)

由初始条件式(19)和边界条件式(20)，并结合式(23)，可计算得到各个节点的Wi(k)值，代入式(22)后，可得到各个节点位置处SO42-质量浓度值ρS,i(t)的近似表达式.

分别取t=100，200，300 d，计算SO42-的侵蚀状况，与有限元结果的对比见图2.由图2可知，近似解的结果与有限元的结果是一致的.此外，随着时间的增长，SO42-逐步向远端侵蚀，对于一个给定位置，其化学物质浓度也随时间增加.

图2　t=100,200,300 d时SO42-的侵蚀深度

由于近初始端的侵蚀情况严重，选取x=0.005 m，考察该处SO42-的质量浓度在时间域上的变化情况，并与有限元结果进行比较，见图3.由图3可见，在运移初期，近似解与有限元解存在偏差，在60 d以后两者就几乎完全重合了.运移初期的偏差主要是由运移时间所致，SO42-要经过一段时间才能到达x=0.005 m处，在此之前，该点处的SO42-的质量浓度为0.而用混合微分变换法进行求解时，是通过初始条件和边界条件，在所有离散点的整个时域t≥0上进行的，得到的是级数解，对溶质的“滞后”现象无法做到完全符合，不过这种偏差会随离散点的增加而减小.

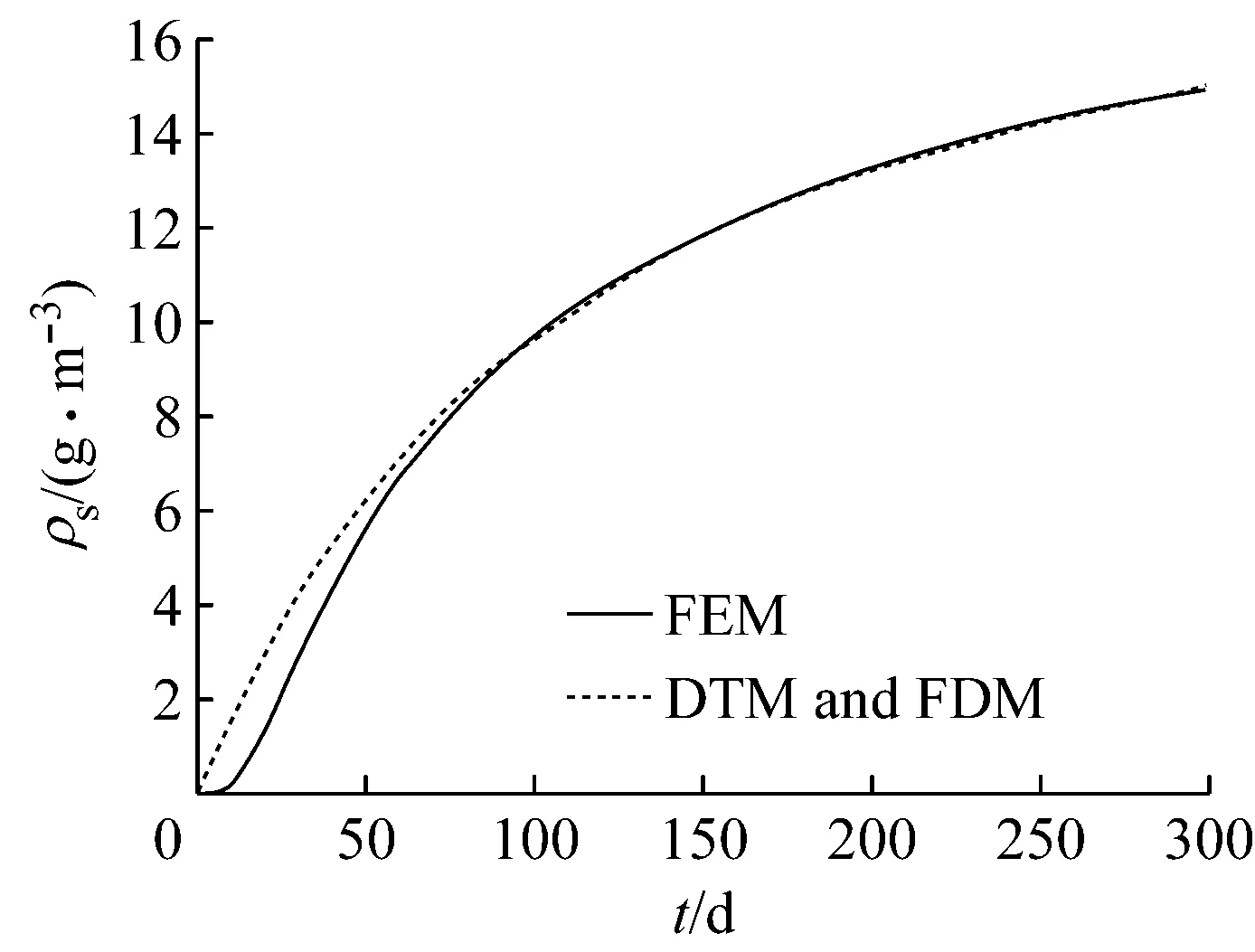
图3　x=0.005 m处SO42-侵蚀深度的结果对比

4.2两种溶质的全耦合运移问题

两种化学物质作用下的耦合溶质运移控制微分方程组[19]为

(24)

式中：ρⅠ和ρⅡ，DⅠ和DⅡ分别为两种化学物质的质量浓度以及扩散系数；RⅠ为阻滞因子；v为对流速度；K为两种化学物质的反应系数.

初始条件:

(25)

边界条件:

(26)

控制方程式(24)在空间各点上的形式为

(27)

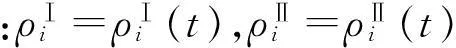
(28)

(29)

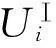
由于算例中SO42-的扩散系数DⅠ较小，取略长的时间t=500，750，1 000 d，考察SO42-的扩散情况，并与有限元计算结果进行比较，见图4.图5为x= 0.005 m处，SO42-的质量浓度在时间域上的变化情况，及其与有限元计算结果的比较.

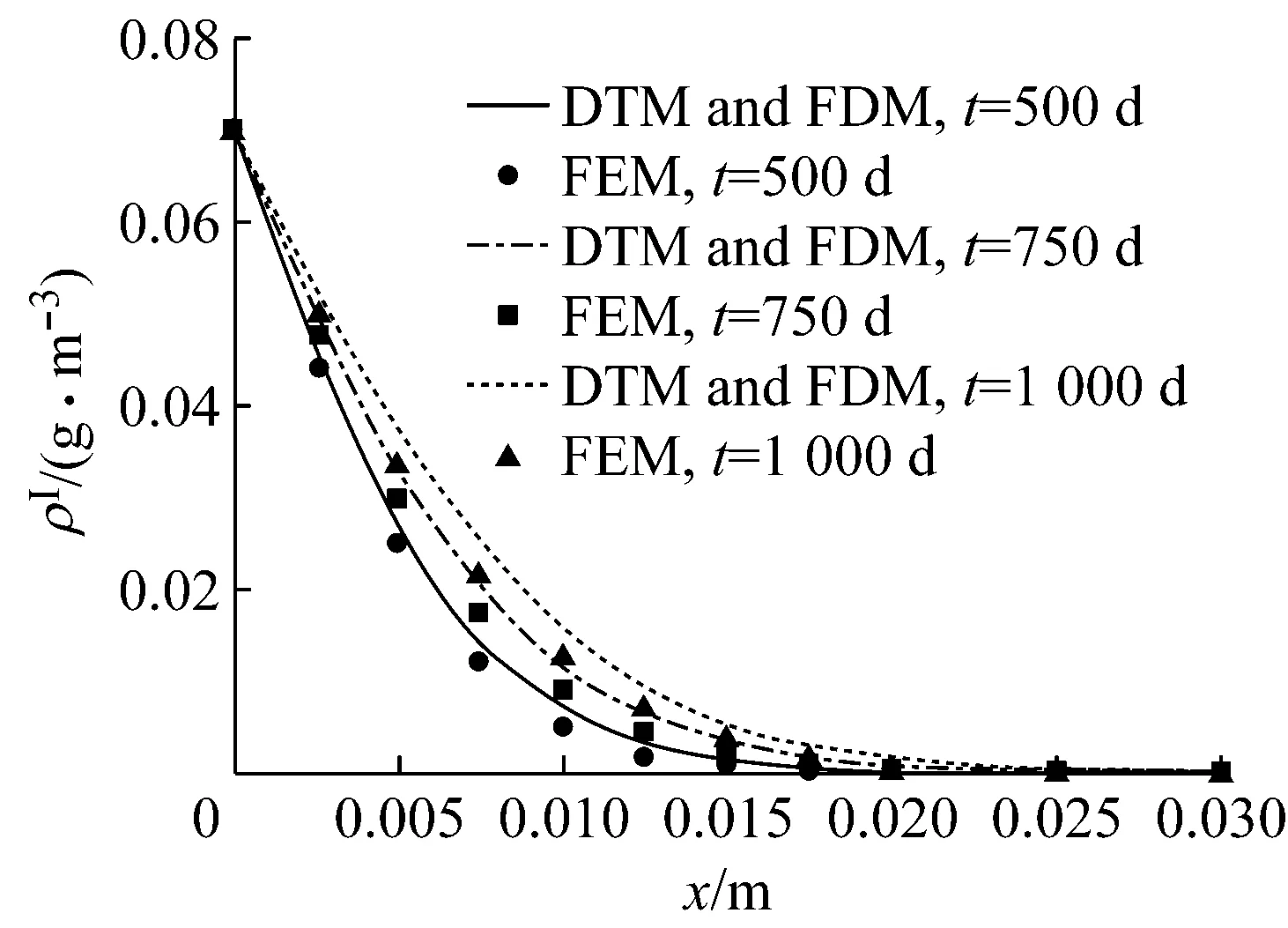
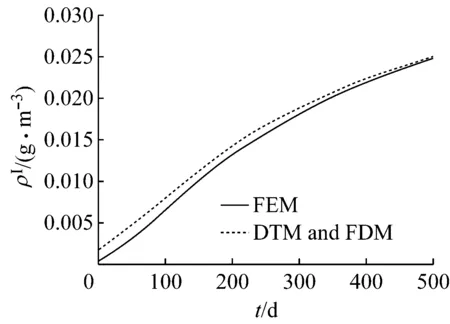
图5　x=0.005 m处SO42-侵蚀深度的结果对比耦合)

Fig.5Concentration of SO42-at 0.005 m

图6为CO2的扩散情况，由于其扩散系数DⅡ相对较大，时间分别取t=20，35，50 d.图7为x= 0.005 m处，CO2的质量浓度在时间域上的变化情况，及其与有限元结果的比较.

图4和6显示近似解与有限元的结果基本一致，且随着时间的增长，SO42-和CO2的逐步向远端侵蚀；随深度的增加，侵蚀速度很快减小.

图6　t = 20, 35, 50 d时CO2的侵蚀深度耦合)

Fig.6Concentration of CO2ast=20, 35, 50 d

由图5和7可知，x= 0.005 m处SO42-和CO2的质量浓度随时间而增加，与4.2节中的情况类似，近似解对溶质的“滞后”现象无法做到完全符合，相对于CO2的扩散情况，由于SO42-的扩散系数较CO2低两个数量级，精度相对较差，导致质量浓度的计算结果偏差略大.

图7　x=0.005 m处CO2侵蚀深度的结果对比耦合)

Fig.7Concentration of CO2at 0.005 m

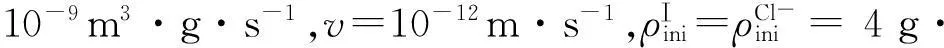
取时间t=20，35，50 d，考察Cl-和CO2的扩散情况，同时考察x= 0.005 m处，Cl-和CO2的质量浓度随时间的变化情况，见图8～11，有限元计算结果也绘于相应的图中.

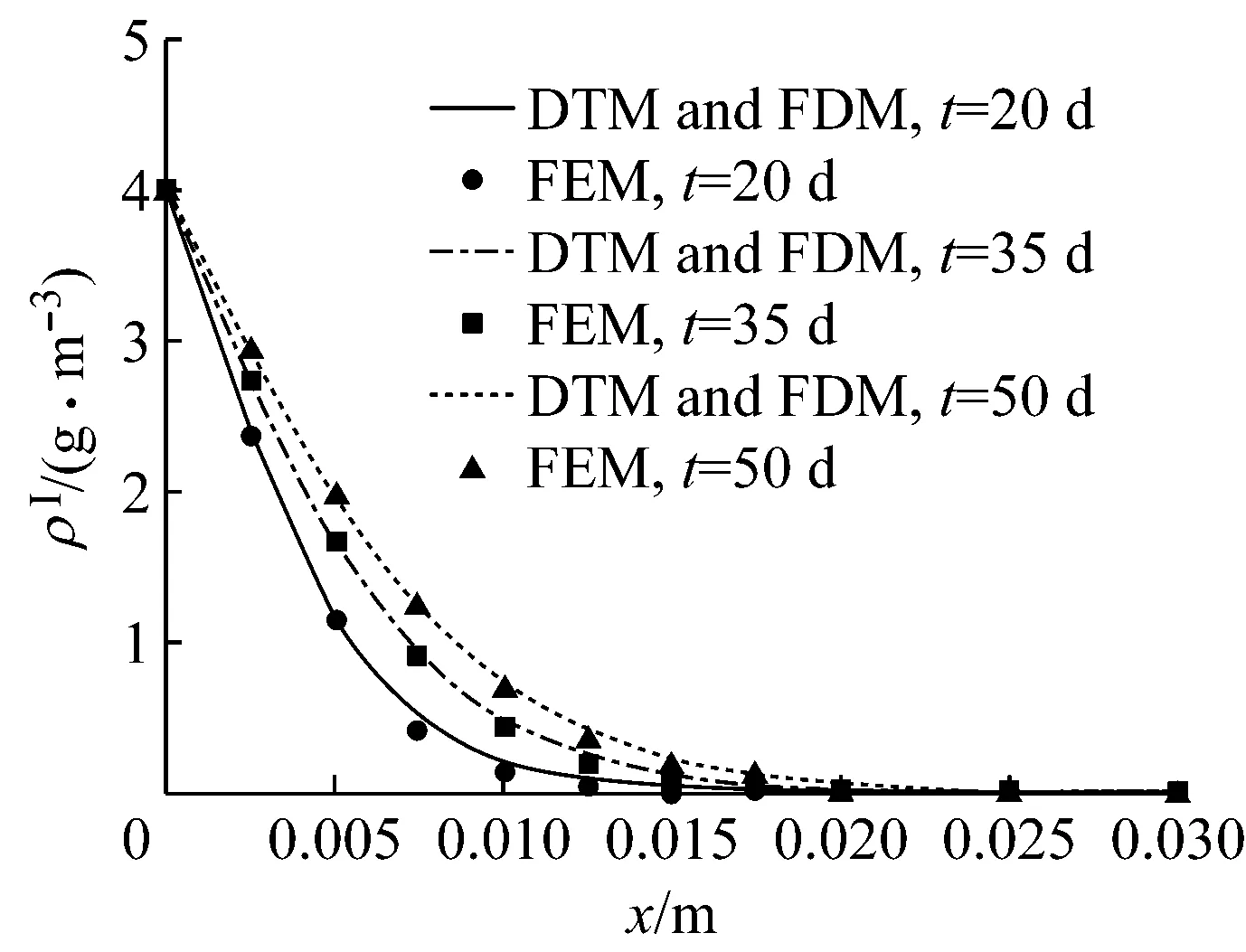
图8　t=20, 35, 50 d时Cl-的侵蚀深度

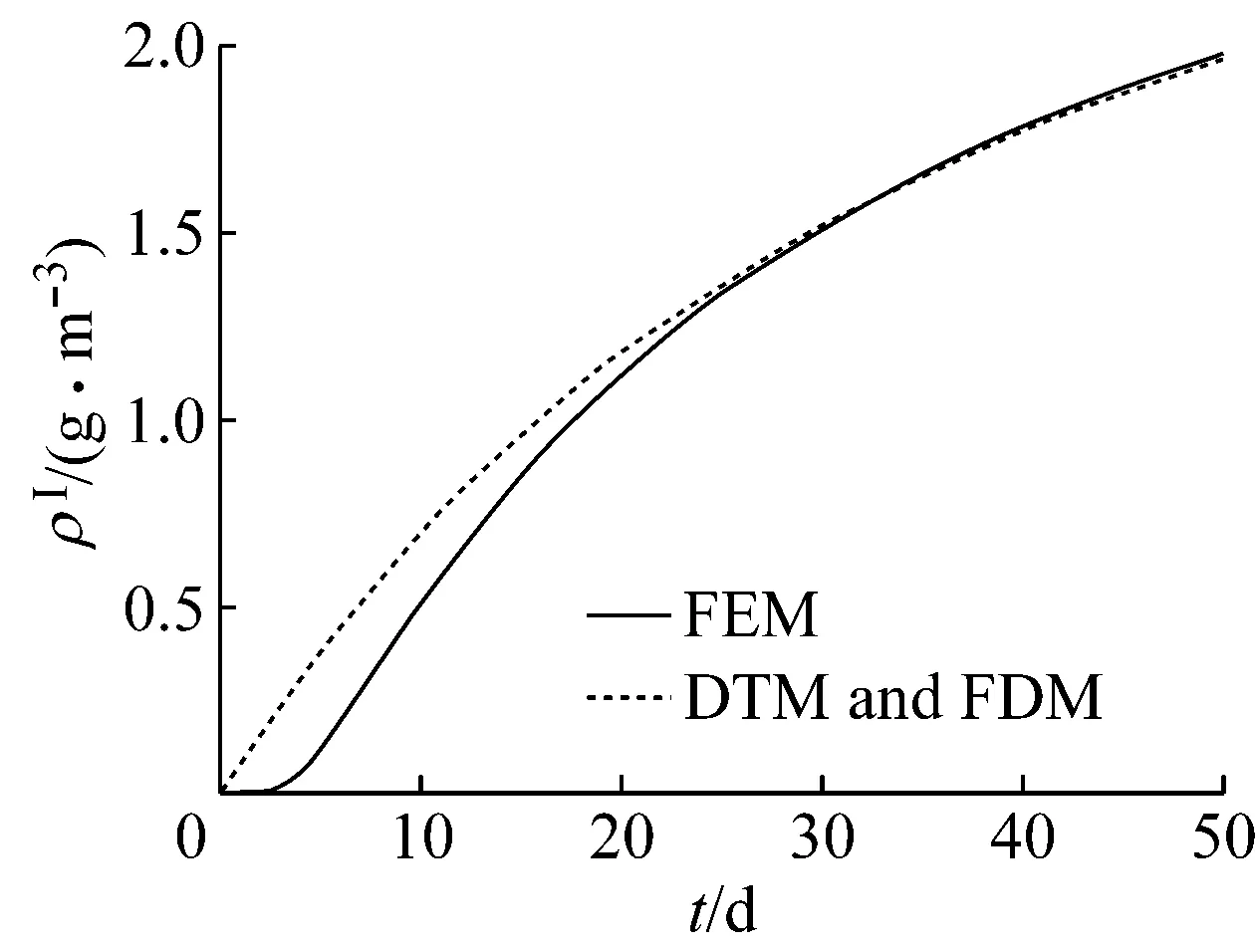
图9　x=0.005 m处Cl-侵蚀深度的结果对比

图10　t = 20, 35, 50 d时CO2的侵蚀深度

图11　x=0.005 m处CO2侵蚀深度的结果对比

5结论

本文利用基于有限差分的微分变换法，解决了混凝土溶质运移问题中，初边值条件间断导致的普通微分变换法求解失效的问题，并用该方法求解了混凝土中SO42-的反应性溶质运移以及CO2-SO42-和CO2-Cl-的全耦合溶质运移问题，得到了问题的近似解，通过与有限元结果的比较，证实了该方法的有效性.

参考文献:

[1]Hope B B, Ip A K C. Chloride corrosion threshold in concrete[J]. ACI Materials Journal, 1987, 84(4): 306.

[2]Loo Y H, Chin M S, Tam C T,etal. A carbonation prediction model for accelerated carbonation testing of concrete[J]. Magazine of Concrete Research, 1994, 46(168): 191.

[3]Somuah S K, Boah J K, Leblanc P,etal. Effect of sulfate and carbonate ions on reinforcing steel corrosion, as evaluated using AC impedance spectroscopy[J]. ACI Materials Journal, 1991, 88(1): 49.

[4]Gospodinov P N, Kazandjiev R F, Partalin T A,etal. Diffusion of sulfate ions into cement stone regarding simultaneous chemical reactions and resulting effects[J]. Cement and Concrete Research, 1999, 29(10): 1591.

[5]窦红. 对流扩散方程的一种显式有限体积-有限元方法[J]. 应用数学与计算数学学报, 2001, 15(2): 45.

DOU Hong. A explicit finite volume-finite element method for nonlinear convection-diffusion problems[J]. Communication on Applied Mathematics and Computation, 2001, 15(2): 45.

[6]左晓宝, 孙伟. 硫酸盐侵蚀下的混凝土损伤破坏全过程[J]. 硅酸盐学报, 2009, 37(7): 1063.

ZUO Xiaobao, SUN Wei. Full process analysis of damage and failure of concrete subjected to external sulfate attack[J].

Journal of the Chinese Ceramic Society, 2009, 37(7): 1063.

[7]Bonakdar A, Mobasher B, Chawla N. Diffusivity and micro-hardness of blended cement materials exposed to external sulfate attack[J]. Cement and Concrete Composites, 2012, 34(1): 76.

[8]赵佳奎. 微分变换及其在电路中的应用[M]. 武汉：华中理工大学出版社, 1988.

ZHAO Jiakui. The application of differential transform method in the circuit problem[M]. Wuhan: Huazhong University of Science and Technology Press, 1988.

[9]Arikoglu A, Ozkol I. Solution of boundary value problems for integro-differential equations by using differential transform method[J]. Applied Mathematics and Computation, 2005, 168(2): 1145.

[10]Özdemir Ö, Kaya M O. Flapwise bending vibration analysis of a rotating tapered cantilever Bernoulli—Euler beam by differential transform method[J]. Journal of Sound and Vibration, 2006, 289(1): 413.

[11]Kangalgil F, Ayaz F. Solution of linear and nonlinear heat equations by differential transform method[J]. Seluk Journal of Applied Mathematics, 2007, 8(1):75.

[12]Shahed M E. Positive solutions of boundary value problems fornth order ordinary differential equations[J]. Electronic Journal of Qualitative Theory of Differential Equations, 2008, 15(1):1.

[13]Chu H P, Chen C L. Hybrid differential transform and finite difference method to solve the nonlinear heat conduction problem[J]. Communications in Nonlinear Science and Numerical Simulation, 2008, 13(8): 1605.

[14]Chen K, Huei Ho S. Solving partial differential equations by two-dimensional differential transform method[J]. Applied Mathematics and Computation, 1999, 106(2): 171.

[15]余红发, 孙伟. 混凝土氯离子扩散理论模型[J]. 东南大学学报: 自然科学版, 2006, 36(2): 68.

YU Hongfa, SUN Wei. Model research on chlorine ion diffusion in concretes[J]. Journal of Southeast University: Nature Science, 2006, 36(2): 68.

[16]Beilina L, Johnsson C. Hybrid FEM/FDM method for an inverse scattering problem[C]∥Numerical Mathematics & Advanced Applications. Milan: Springer, 2003:545-556.

[18]张文生. 科学计算中的偏微分方程有限差分法[M]. 北京: 高等教育出版社, 2006.

ZHANG Wensheng. Finite difference methods for partial differential equations in science computation[M]. Beijing: Higher Education Press, 2006.

[19]Liang M T, Lin S M. Modeling the transport of multiple corrosive chemicals in concrete structures: synergetic effect study[J]. Cement and Concrete Research, 2003, 33(12): 1917.

Application of Hybrid DTM and FDM in Solute Transport Problem of Concrete

ZHONG Xinran, DAI Ying, CHEN Xi

(College of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092， China)

Abstract：The differential transform method (DTM) ceases to be effective when solving the solute transport equation with discontinuous condition. In order to solve this problem, hybrid DTM and finite difference method(FDM) were adopted to solve the solute transport equation of SO42-, coupled CO2- SO42-and coupled CO2-Cl- of concrete, and the approximate solutions were obtained. The comparison of the results with those obtained by FEM shows that the proposed method is effective to obtain the approximate solution of solute transport problem.

Key words：concrete; solute transport; finite difference method(FDM); differential transform method(DTM)

收稿日期：2015-06-23

基金项目：国家“九七三”重点基础研究发展计划(2011CB013800)

通讯作者：戴瑛(1966—)，女，教授，博士生导师，工学博士，主要研究方向为计算力学.E-mail:ydai@tongji.edu.cn

中图分类号：TU37

文献标志码：A

第一作者： 钟新然(1992—)，男，博士生，主要研究方向为混凝土多场耦合. E-mail:101839@tongji.edu.cn