混凝土单轴受压全过程变异性试验研究

晏小欢， 任晓丹， 李　杰

(同济大学 土木工程学院， 上海 200092)



混凝土单轴受压全过程变异性试验研究

晏小欢， 任晓丹， 李杰

(同济大学 土木工程学院， 上海 200092)

摘要：为了研究混凝土在单轴受压作用下的全过程受力特征，通过对强度等级为C30～C60的60个混凝土棱柱体试件进行单轴受压应力-应变全曲线试验，得到了单轴受压作用下混凝土峰值强度、峰值应变、弹性模量和应力-应变全曲线的统计特征.根据混凝土结构设计规范(GB50010—2010)中的混凝土峰值强度变异系数，利用概率密度演化方法，获得了混凝土应力均值曲线和应力标准差曲线.通过与试验结果进行对比，认为仅用峰值强度的变异系数不足以描述混凝土应力-应变全过程的随机性，建议给出标准差曲线.

关键词：混凝土； 试验研究； 本构关系； 随机性

混凝土的应力-应变全曲线试验是研究混凝土在外部作用下的强度、变形和破坏机理的基础.从20世纪中期开始，国内外已经进行了大量的混凝土单轴受压试验[1-6].这些结果清楚地体现了混凝土应力-应变全过程曲线的非线性特征.1988年，Mander等[7]在总结大量实验研究结果的基础上，提出了混凝土受力全过程曲线的经验表达式，这一表达式被欧美国家的学者所普遍接受.1997年过镇海[8]详细总结了混凝土单轴受压全过程试验的基本特征，建议的混凝土应力-应变全过程曲线的经验表达式被我国混凝土设计规范所采用.然而，现有研究工作大多忽略了混凝土受力力学行为的另一重要性质——随机性.事实上，近期针对混凝土单轴受压破坏概率模型的分析也仅针对混凝土强度的概率统计[9].专门研究混凝土在单轴受力过程中随机性的试验研究尚未成为研究者关注的重点.为此，本文将着重通过同强度等级的批量混凝土单轴受压全过程试验，研究揭示混凝土受力力学行为的随机性特征.

1试验内容

1.1试件制作

试验所用混凝土采用实际工程中使用的商品混凝土，试件根据强度等级分4批制作，每批浇筑5个标准立方体试件(150 mm×150 mm×150 mm)和20个标准棱柱体试件(150 mm×150 mm×300 mm).试验用商品混凝土用最大粒径为25 mm的碎石作为粗骨料，每立方米混凝土中材料用量及配合比如表1所示.试件浇筑24 h后拆模，放入养护室内养护，养护时间为28 d.

表1　混凝土配合比

1.2试验设备

试验在同济大学建筑结构试验室进行并完成.试验采用的加载系统为MTS815力学性能试验系统，该试验系统最大压力可达到2 700 kN，最大加载速率为30 mm·s-1，试验机机架刚度为9×109N·m-1，系统设置自动动态控制模式转换，可实现力控制加载与位移控制加载平滑切换.试验采用的测量系统包括用于测量应变的引伸计以及安装在MTS815试验机机架上的载荷传感器和位移传感器.试验中采用的引伸计为轴向引伸计，测量试件在受力过程中的轴向应变，引伸计的测量标距为100 mm，最大测量应变值为0.04 mm·mm-1，测量精度为1/10 000 mm.

1.3试验过程

在我国规范中，混凝土强度等级由立方体抗压强度标准值确定，而弹性模量在一定程度上能反映混凝土材料的变形性能.因此，本次试验内容包括混凝土立方体抗压试验、弹性模量试验和棱柱体单轴受压应力-应变全曲线试验.

混凝土力学性能试验参照《普通混凝土力学性能试验方法》(GB/T50081—2002)相应规定的方法进行[10].全曲线试验根据试件的混凝土强度等级确立加载程序.加载过程采用力加载和位移加载混合控制，设混凝土材料抗压强度为fc，试验的加载步骤为：力控制0 MPa→0.1fc→0 kN→0.1fc→0 kN位移控制→3 mm.具体试验步骤为：

(1) 试件准备.试件从养护地点取出后，先将试件表面与上下承压板面擦干净，当试件加载面不平整时，可采用打磨工具打磨平整.

(2) 安装轴向引伸计.采用与试件成型时顶面垂直的对称侧面安装引伸计，安装引伸计前插上定位针，引伸计安装在侧面中线上并对称于试件的两端(图1).

(3) 试件放置就位和对中.将试件安放在试验机的承压板上，试件的中心应与试验机下压板中心对准(图2).

(4) 试件预压.手动控制试验机加载位移，当下压板上升到试件与上压板接近时，拔出引伸计定位针，施加预压力约0.5 MPa，检查试件对中情况，并作适当调整.

(5) 试件正式加载.调整初始读数为零，运行上述提前设置好的加载程序，开始试验，通过计算机实时观测同步数据.

图1　安装轴向引伸计

图2　试件就位和对中

1.4试验现象

试件加载过程中，可以通过试验机的力、位移传感器及引伸计观测力和变形的发展，同时对试验过程进行摄像以记录试件表面裂缝的扩展.为了便于进行分析和比较，将试验所得典型单轴受压应力-应变曲线用量纲一化坐标轴绘制，以C40为例，见图3.由图3可见，现阶段使用的商品混凝土试验与已有的混凝土试验相比，其单轴受压全过程试验非线性发展过程具有相同的变化特征.按照这一变化特征，可以将曲线的变化过程分为5个阶段：

阶段1为线弹性阶段(A点到B点)，0<σ/fc<0.4(σ为受压全过程的应力，fc为峰值应力)，图3中B点的应变相对值ε/εc≈0.25(ε为受压全过程的应变，εc为峰值应变).在这个阶段，应力-应变关系近似为线性，表面尚未出现肉眼可见裂缝.

阶段2为非线性上升阶段(B点到C点)，0.4<σ/fc<1.0，C点的应变相对值ε/εc=1.0，为应力峰值点.在0.4<σ/fc<0.8，曲线开始趋于非线性，是线性到非线性过渡段，在0.8<σ/fc<1.0时，非线性程度明显，此时表面依然无肉眼可见裂缝.

阶段3为非线性下降阶段(C点到D点)，σ/fc范围为1.0→0.6，D点的应变相对值ε/εc≈(1.8～2.5).在应力从峰值点下降到σ=0.9fc时，在表面的角部出现第一条细小可见裂纹，此后随着变形的增加，应力下降，第一条裂纹继续延伸和增宽，到σ=0.6fc时，肉眼可见且非常明显.

阶段4为反向弯曲阶段(D点到E点)，σ/fc范围为0.6→0.3，E点的应变相对值ε/εc≈(3.0～4.0).在这一阶段，应力-应变曲线的凹凸性发生变化，D点近似为线型变换的拐点.在第一条裂纹继续发展、延伸的同时，在表面会逐渐出现和发展若干条裂纹，方向与加载方向平行或小于截面对角线与加载方向的夹角.

阶段5为完全破坏阶段，σ/fc范围为0.3→0.1.在这一阶段，裂缝宽度明显增加、延伸，当一到两条主要裂缝贯穿整个截面时试件破坏.

图3　混凝土单轴受压本构曲线

2试验结果分析

2.1立方体抗压强度与弹性模量

立方体抗压试验采用标准立方体试件(150 mm×150 mm×150 mm)，共完成4组试验,每组5个试件.每组试验的立方体强度均值、均方差和变异系数见表2.从表2中可见，由于工程中存在质量控制要求，商品混凝土的立方体抗压强度一般偏高，混凝土的立方体抗压强度的变异系数随强度等级的变化趋势不明显.

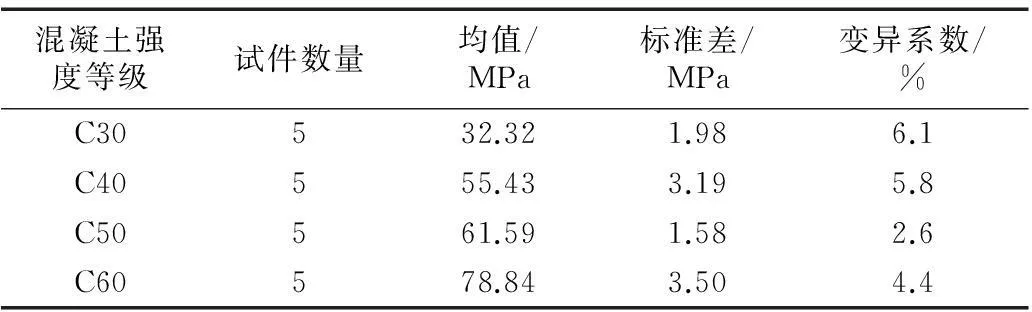
表2　立方体抗压强度试验结果

弹性模量试验采用标准棱柱体试件(150 mm×150 mm×300 mm)，共完成4组试验,每组试验3个试件，试验得到每组试件的弹性模量均值，试验结果见表3.从表3可以看到，随着混凝土强度的增加，除了C50弹性模量偏小，弹性模量总的趋势是增加的，因为本次试验每组试件数量仅为3个，可能会因此而产生偏差.

表3　弹性模量试验结果

2.2单轴受压应力-应变全曲线分析

单轴受压全过程试验共获得单轴受压应力-应变全曲线64条，通过对同组试验数据进行等应变选点，可以计算出相同强度等级混凝土的应力-应变全曲线应力均值为[11]

(1)

(2)

将同一强度等级混凝土试验所得的应力-应变全曲线、均值曲线以及标准差曲线绘于同一图中，见图4.分析试验结果可见，混凝土单轴受压全过程试验结果存在明显的离散性.图5，6分别为试验所得单轴受压应力-应变均值曲线和标准差曲线.从图5可见，混凝土强度越大，应力-应变均值曲线上升段和下降段越陡峭.从图6可见，应力标准差有随强度增加而增高的趋势.具体而言，在应力-应变曲线上升段，应力标准差逐渐增加，在峰值强度附近达到最大值，随后随着应力的减小而减小，到应力σ=0.9fc后基本保持常数.

a C30

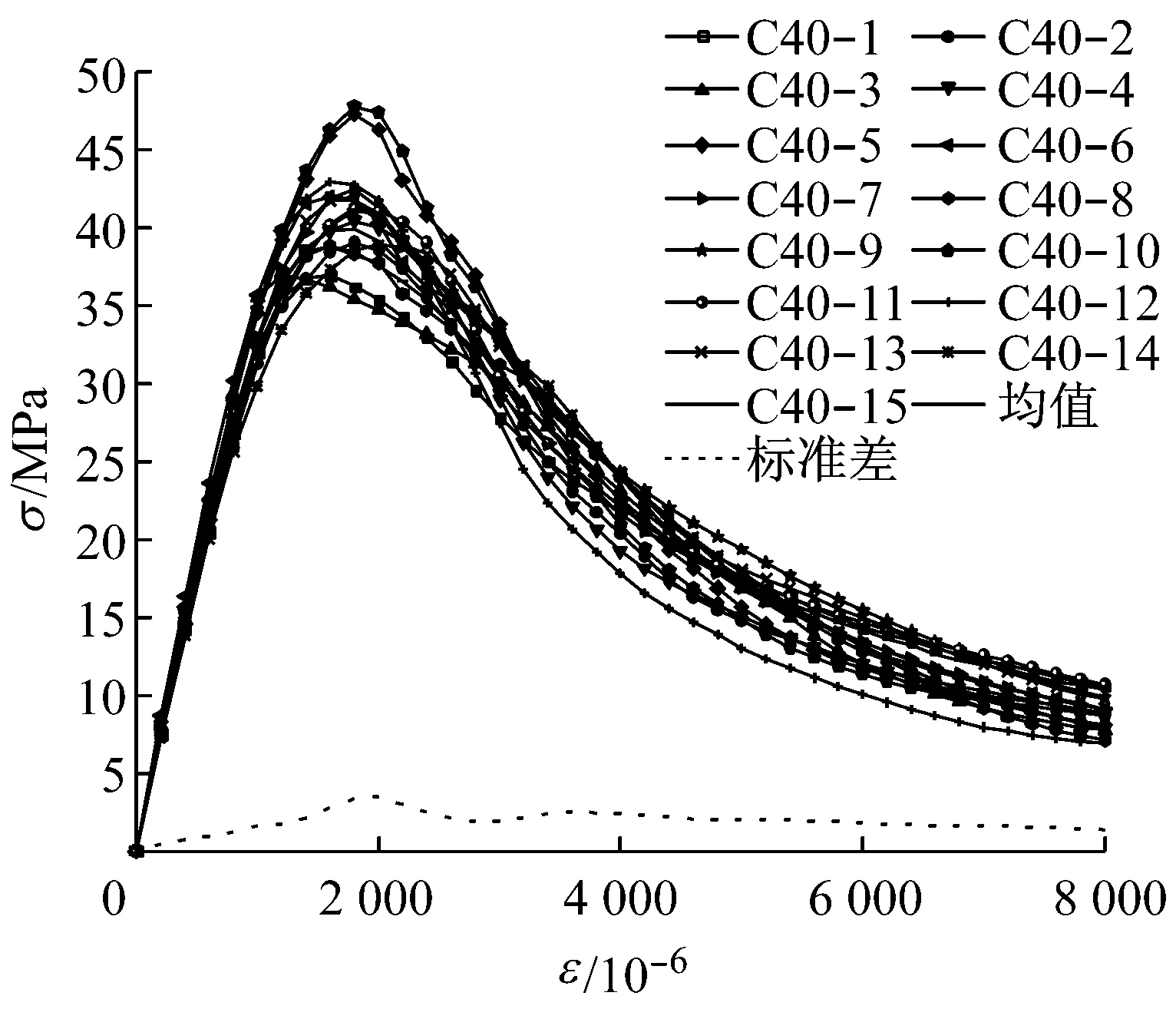
b C40

c C50

d C60

图5　混凝土应力-应变均值曲线

试验所得单轴受压峰值强度见表4.从表4中可以看到，混凝土峰值强度的标准差随强度增加而略有增加，变异系数的变化趋势不明显.试验所得单轴受压峰值应变试验结果见表5.从表5可见，峰值应变、标准差和变异系数随混凝土强度等级的变化趋势并不明显.

图6　混凝土应力标准差曲线

表4　单轴受压强度试验结果

表5　单轴受压峰值应变试验结果

3试验结果与现行规范的比较

混凝土单轴受压的应力-应变曲线按《混凝土结构设计规范》(GB50010—2010)C.2.4的公式及条文说明中的公式进行计算[12].

(3)

(4)

(5)

(6)

(7)

(8)

(9)

式中：dc为混凝土单轴受压损伤演化参数；Ec为混凝土的弹性模量；αc为混凝土单轴受压应力-应变曲线下降段参数值；fc为混凝土单轴抗压强度值；εc为与单轴抗压强度相应的混凝土峰值压应变.

《混凝土结构设计规范》(GB50010—2010)条文说明附录C表2中给出了混凝土强度变异系数，对应于混凝土强度等级为C30，C40，C50，C60的混凝土强度变异系数分别为17.2%，15.6%，14.9%和14.1%.据此，采用概率密度演化理论，可以对混凝土应力-应变本构关系作出概率密度演化的描述，并获得混凝土应力-应变全过程的应力标准差.具体做法是：根据规范规定的混凝土本构关系计算公式(3)，取应变ε为广义时间参数，应力σ为状态变量，结合以下广义密度演化方程[13-14]：

(10)

式中：Θ为随机参数，其概率密度函数为pΘ(θ).求解应力概率密度随应变的演化过程.式(10)的数值求解基本步骤为：

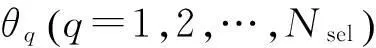
(2) 计算目标量.目标量应力σ由公式(3)～(9)计算得到.

(3) 求解概率密度.根据概率密度演化方程(10)的数值解法，计算给定应变处应力的均值和标准差并绘出曲线.

(4) 计算给定应变处所对应应力的概率密度数值解，绘出应变区间应力的概率密度演化等值线图.由概率密度分布，容易计算给出均值与方差曲线.

以C30为例，由表4得到混凝土强度均值为22.23 MPa，规范给定C30混凝土强度变异系数为17.2%，选取代表点数量Nsel=100，计算结果如图7所示.

同理，可得到混凝土强度等级为C40～C60的混凝土应力-应变曲线，将4个强度等级的应力均值曲线统一绘于图8.

对比图5与图8可见，试验所得峰值应变随混凝土强度等级的增加变化趋势不明显，而规范所得峰值应变随混凝土强度等级的增加明显增加.对峰值应变随混凝土强度等级的变化情况进行对比研究，并将对比结果绘于图9中.从图9可见，不同试验所得峰值应变随混凝土强度等级的增加变化均不明显，而规范中峰值应变随强度等级增加明显增加，说明规范中对峰值应变随强度等级增加而增加的规定值得商榷.

将计算所得混凝土应力标准差曲线统一绘于图10(混凝土强度等级为C30～C60).对比图6和图10可见，试验标准差与上述按规范计算的标准差曲线也明显不同：前者在混凝土达到峰值强度后大体稳定，后者则随应力水平降低而降低.其原因在于规范以强度变异系数规定了混凝土应力-应变曲线全过程的变异性.

a 应力均值和标准差

b 应力概率密度演化等值线

图8　规范(GB 50010—2010)所得混凝土应力-

图9　峰值应变随混凝土强度等级变化情况

图10　规范(GB 50010—2010)所得混凝土应力标准差曲线

4结论

本文以考察混凝土受力力学行为的随机性为目的，分别对混凝土强度等级为C30，C40，C50，C60的商品混凝土进行了单轴受压应力-应变全过程试验，据此详细研究了不同强度等级的商品混凝土在单轴受压作用下的应力-应变全曲线随机性特征，并与规范相关规定进行了对比分析.研究结论表明：

(1) 混凝土单轴受压全过程的随机性不容忽视.

(2) 可以认为峰值应变不随混凝土强度发生变化；现行规范中混凝土受压峰值应变随强度增高而增大的结论值得商榷.

(3) 采用强度变异系数表示应力-应变曲线的离散性并不合适.在峰值强度之后，混凝土应力-应变曲线的标准差可近似取为常数.

参考文献:

[1]Popovics S. A review of stress-strain relationships for concrete [J]. ACI Journal Proceedings, 1970, 67(3): 243.

[2]Watanare E. Complete stress-strains curve for concrete in concentrical compression [J]. Mechanical Behavior of Materials, 1972, 4: 153.

[3]曹居易. 混凝土的应力应变关系[J]. 四川建筑科学研究, 1979, 1: 1.

CAO Juyi. The stress-strain relationship of concrete [J]. Building Science Research of Sichuan, 1979, 1: 1.

[4]过镇海, 张秀琴, 张达成, 等. 混凝土应力-应变全曲线的试验研究 [J]. 建筑结构学报, 1982, 3(1): 1.

GUO Zhenhai, ZHANG Xiuqin, ZHANG Dacheng,etal. Experimental investigation of the complete stress-strain curve of concrete[J]. Journal of Building Structures, 1982, 3(1): 1.

[5]张德思. 混凝土应力-应变全曲线的试验研究 [J]. 湖南大学学报, 1982, 9(4): 58.

ZHANG Desi. Test research on complete stress-strain curve of concrete[J]. Journal of Hunan University, 1982, 9(4): 58.

[6]杨木秋, 林泓. 混凝土单轴受压受拉应力-应变全曲线的试验研究[J]. 水利学报, 1992, 6: 60.

YANG Muqiu, LIN Hong. Test study on stress-strain curve of concrete under uniaxial compressing and tensile[J]. Journal of Hydraulic Engineering, 1992, 6: 60.

[7]Mander J B, Priestley M J N, Park R. Theoretical stress strain model for confined concrete [J]. Journal of Structural Engineering, ASCE, 1988, 114(8): 1804.

[8]过镇海.混凝土的强度和变形——实验基础和本构关系[M]. 北京: 清华大学出版社, 1997.

GUO Zhenhai. Strength and deformation of concrete-experimental foundation and constitutive relationship [M].Beijing: Tsinghua University Press, 1997.

[9]王凤武, 楼梦麟, 徐人平, 等.混凝土单轴受压强度可靠度与置信度研究[J]. 四川建筑科学研究, 2004, 2: 89.

WANG Fengwu, LOU Menglin, XU Renping,etal. A study of probability and confidence for concrete strength [J]. Sichuan Building Science, 2004, 2: 89.

[10]中华人民共和国住房和城乡建设部，国家质量监督检验检疫总局. GB/T 50081—2002 普通混凝土力学性能试验方法标准[S]. 北京: 中国建筑工业出版社, 2003.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China. GB/T 50081—2002 Standard for test method of mechanical properties on ordinary concrete[S]. Beijing: China Architecture & Building Press, 2003.

[11]Ren X D, Yang W Z, Zhou Y,etal. Behavior of high-performance concrete under uniaxial and biaxial loading [J]. ACI Materials Journal, 2008,150 (6):548.

[12]中华人民共和国住房和城乡建设部. GB50010—2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB50010—2010 Code for design of concrete structures[S]. Beijing: China Architecture & Building Press, 2011.

[13]Li J, Chen J B. The principle of preservation of probability and the generalized density evolution equation[J]. Structural Safety, 2008, 30: 65.

[14]曾莎洁, 李杰. 混凝土单轴受压本构关系的概率密度描述[J]. 同济大学学报:自然科学版, 2010, 38(6): 798.

ZENG Shajie, LI Jie. Analysis on constitutive law of plain concrete subjected to uniaxial compressive stress based on generalized probability density evolution method[J]. Journal of Tongji University: Natural Science, 2010, 38(6): 798.

[15]张玉敏. 不同应变率下混凝土力学性能的试验研究[D]. 北京: 北京工业大学, 2012.

ZHANG Yumin. Experimental study of the mechanical properties of concrete under different strain rates[D]. Beijing: Beijing University of Technology, 2012.

[16]曾莎洁. 混凝土随机损伤本构模型与试验研究[D]. 上海: 同济大学, 2012.

ZENG Shajie. Dynamic experimental research and stochastic damage constitutive model for concrete[D]. Shanghai: Tongji University, 2012.

Experimental Study of Full Process Variability of Concrete Under Uniaxial Compression

YAN Xiaohuan, REN Xiaodan, LI Jie

(College of Civil Engineering, Tongji University, Shanghai 200092, China)

Abstract：An experimental research was performed to investigate the behavior of concrete under uniaxial compression. A total of 60 prism specimens of which the strength grade ranges from C30 to C60 were tested using the MTS testing system. Based on the experimental results, the statistical characteristics of peak strengths, peak strains elastic modules and the complete stress-strain curves were obtained. Then, the randomness of concrete was studied theoretically according to the variation coefficient of strength specified in Chinese code (GB50010-2010). The mean curves and standard deviation curves were obtained based on the generalized probability density evolution method. The comparison between the experimental and theoretical results indicate that it is inadequate to represent the randomness of concrete only by the variation coefficient of strength. Finally, the standard deviation curves were proposed based on experiment results.

Key words：concrete; experiment research; constitutive relationship; randomness

收稿日期：2015-06-30

基金项目：国家自然科学基金(51261120374，91315301，51208374)

通讯作者：李杰(1957—)，男，教授，博士生导师，工学博士，主要研究方向为随机动力学,混凝土损伤力学和工程系统可靠度.

中图分类号：TU528.01

文献标志码：A

第一作者： 晏小欢(1984—)，女，博士生，主要研究方向为混凝土本构关系理论与试验.E-mail：yan_xh1223@163.com

E-mail：lijie@tongji.edu.cn