纵振激振面积对条纹振动矩形板声场指向性的影响

刘豆豆, 贺西平, 李家星

(陕西师范大学 物理学与信息技术学院， 陕西 西安710119)



纵振激振面积对条纹振动矩形板声场指向性的影响

刘豆豆, 贺西平*, 李家星

(陕西师范大学 物理学与信息技术学院， 陕西 西安710119)

摘要：在大功率超声应用中，纵振激振换能器与阶梯板间有一定接触面积，导致振动节线与凸台边缘不重合。利用数值计算和有限元分析相结合的方法，研究了(8,0)条纹振动模式下激振源面积大小对矩形板声场指向性的影响。结果表明，对尺寸为180 mm×120 mm×5 mm(长×宽×厚)的矩形薄板，随着激振源半径增大，条纹振动节线逐渐弯曲，(8,0)模态共振频率增大，指向性尖锐程度减小。当观察平面垂直于矩形板表面时，沿y轴方向指向性更为尖锐。当半径增大到12 mm时，副瓣已明显出现，故对该矩形板，应选择激振源半径在8 mm以内。

关键词:有限元法；矩形板；激振源面积；节线；指向性

辐射体的声场指向性在大功率超声应用中是一个重要问题，研究者对此进行了大量研究。文献[1]对楔形换能器远场作了分析和实验，理论上给出了介质表面的瑞利波指向性图案。何正耀等利用边界元理论计算了水声换能器阵的指向性，并进行了实验验证[2]。文献[3-5]计算了圆柱壳类声场的指向性。贺西平等计算了节圆与阶梯凸台位置重合时，阶梯圆盘声场的指向性[6]。文献[7]测量了激励面积较小时阶梯型矩形板的声场指向性。文献[8]利用声场迭加原理推导出了阶梯圆盘辐射声压，并计算了面激振时(即激励换能器与辐射盘之间有一定面积大小相联接)节圆偏离阶梯位置对声场指向性的影响。文献[9]计算了纵振激振面积不同对矩形薄板振动特性的影响。

纵振-弯曲辐射体振动和辐射系统由Gallego等提出，此类换能器综合了纵振换能器的高效率和弯曲振动平圆盘大辐射面积的特点，能有效地与空气介质进行阻抗匹配并辐射强功率超声[10]。平圆盘弯振时节线两侧相位相反，导致声场指向性变差，文献[11-13]在该平圆盘节线两侧反相位区域增加辐射介质中声波波长1/2的高度变为阶梯状。此类阶梯状辐射体类似于活塞振动盘，振动面上的各部分振动相位相同。激振换能器与该阶梯圆盘接触面积很小(可视为点接触)，激振频率为该阶梯圆盘本征频率时，阶梯圆盘节线位置与阶梯位置相重合，辐射声场指向性尖锐[14-15]。在振动面内，矩形板比圆形板振幅分布更加均匀，应力分布也较均匀，可以承受更大的机械强度。同理，可以在矩形板本征条纹弯曲振动模式的基础上，改进成为阶梯板。纵振换能器在其本征频率点接触激振该板中心，换能器的振动几乎不影响阶梯板弯曲振动特性，此时振动节线将与阶梯边缘位置重合，辐射声场具有尖锐指向性。实际应用中，尤其是大功率状态下，激振换能器一般与辐射盘或板肯定有一定的接触面积， 即为面接触激振。面接触激振时，就会导致板的节线与预设的阶梯位置不重合。

本文以矩形板为例，研究在自由边界条件下， (8,0)模态节线和预设阶梯位置不重合时的辐射声场指向性。将瑞利积分公式离散化，结合有限元方法计算矩形板的振动模态，提取其各有限单元上的振动位移，再利用声场迭加原理，计算研究激振源面积变化对矩形板辐射声场指向性的影响。发现面激振的矩形板振动节线变形而不再保持为直线，且接触面积越大，节线弯曲也越明显[16]。计算结果为分析面激振下阶梯形矩形板节线偏离预设阶梯位置对指向性的影响提供了参考。

1矩形板的振动特性

取材料为45#钢，尺寸为(180×120×5)mm(长×宽×厚)的矩形板,其杨氏模量E=2.16×1011N2/m，泊松比δ=0.28，密度ρ=7 800 kg/m3。空气中声速为340 m/s，对应(8,0)模态本征振动频率为20 216 Hz，振动节线基本为直线。按照此时的直节线分布将矩形板改进成阶梯形，若仍为点源激振，阶梯形矩形板的振动节线将与阶梯边缘的位置相一致，但若面激振改进后的阶梯形矩形板，则板的振动节线将弯曲变形不再与预设的阶梯边缘重合。

图1为激振源半径为r=16 mm时，矩形板弯曲振动振型图，在该振型图上，依照(8,0)本征模态直振动节线位置在图1上标注，从左至右共八条，其中第1、2条，3、4条，5、6条以及7、8条直线之间为预设的加阶梯位置，所加阶梯的高度为介质中辐射声波波长的1/2。换能器面激振矩形板，条纹振动模式时，节线扭曲变形偏离原直节线位置，阴影部分表示不加阶梯时矩形板面激振下相位为负的区域，空白部分表示相位为正的区域，阴影部分的边缘线即为扭曲后的节线。也就是说，面激振时，振动节线不再保持为直线而呈现弯曲状。从左至右共有8条，从小到大依次编号，原第1、2、7、8条节线中间部分已经断开，第3条、第6条节线弯曲程度较大，中间部分分别与第2条和第7条节线相交，第4条、第5条节线弯曲程度较大，整个矩形板振型复杂。

2声场指向性计算方法

图2为用于计算弯曲振动矩形板声场指向性的几何示意图，假设该弯曲振动矩形板嵌在无限大障板上，弯振时会向z轴正向的无限大半空间内辐射声波，其中A为声场中任意观察点，直角坐标和球坐标分别为(x0,y0,z0)和(r,θ,φ)，ds为矩形薄板上一微小面元，ds=dxdy,r为观察点A与坐标原点O之间距离，h为观察点到面元距离。

由图2可知,观察点与面元ds间距为

(1)

通过瑞利积分公式，有面元ds在观察点A处产生的声压为

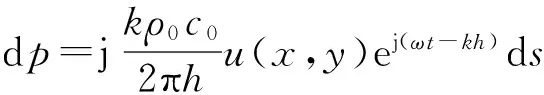
(2)

其中u(x,y)表示面元处的振速幅值。将所有点源辐射声波进行叠加可得

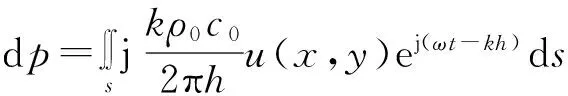
(3)

对于r≫ω和l的远场区域，不考虑矩形板自身尺寸，上式中振幅部分的h可近似用板中心到观察点距离r来替代。结合远场条件，近似表示为

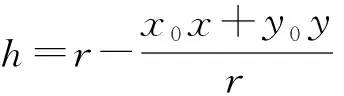
(4)

观察点A所处的方向角为

cosα=x0/r=sinθcosφ，

cosβ=y0/r=sinθsinφ。

(5)

将(4)、(5)两式代入声压表达式(3)可得

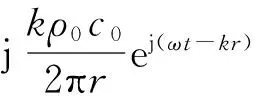
[(cos(kxsinθcosφ)cos(kysinθsinφ)-

sin(kxsinθcosφ)sin(kysinθsinφ))+

j(cos(kxsinθcosφ)sin(kysinθsinφ)+

cos(kysinθsinφ)sin(kxsinθcosφ))]dxdy。

(6)

令

(7)

离散上述两式得

A点的声压幅值表达式为

(9)

其中：N为离散后组成振动面的单元总数，Δsi为第i个单元的面积，vi表示第i个单元的中心点速度，xi、yi为第i个单元的横坐标和纵坐标，这些量可以从有限元数值计算中获取。

在有限元模态计算模块，提取板辐射表面各单元挠度Li。假设矩形板为小挠度简谐振动，则板的横向位移可表示为

η=Liejωt。

(10)

由此可得矩形板表面各单元振速为

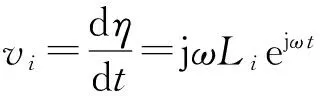
(11)

将(11)式带入(8)式计算弯曲振动矩形板辐射声场指向性表达式为

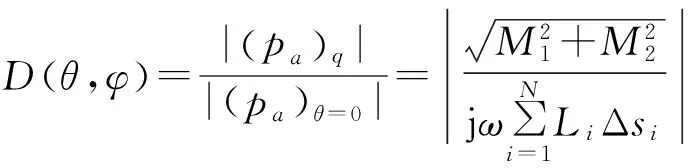
(12)

结合(8)、(12)式，提取振动位移后，对位移值进行处理，如图1中所示，将预设加阶梯部分的负相位位移值全部变为正值，正相位位移值全部变为负值，未加阶梯部分位移值相位不变，将处理后的数据汇总，编制程序计算得到面激振情况下矩形板弯曲振动辐射声场指向性。

3计算结果及分析

3.1纵振激振源点激励矩形板

利用有限元方法得到本征频率下弯曲振动矩形板(8,0)模态振型图，如图3a所示，矩形板各弯振节线基本为直线，阴影部分两侧相邻节线位置即为预设阶梯的边缘位置。提取矩形板前表面各面元位移值代入计算指向性程序中，得到观察平面垂直于矩形板表面并分别沿x轴和y轴方向的指向性如图3b、3c所示。

可以看出，不加阶梯情况下，矩形板(8,0)模态声场指向性较差，如3b所示，观察平面垂直于矩形板表面并沿x轴方向时，指向性图案中在θ=0方向上没有主瓣，即轴线方向上没有声能量辐射。3c中观察平面沿y轴时，指向性图案中在θ=0方向上出现主瓣，但在其他方向有较大副瓣，在指向性要求高的场合无法使用。若以阴影部分的边缘直线为界给矩形板增加高度为空气中声波波长1/2的阶梯成为活塞板，则图3a中矩形板阴影部分的负相位位移反相，整个辐射表面振动相位基本都为正值，本文对预设加阶梯部分的位移值进行反向处理后计算得加阶梯矩形板的指向性如图4所示。

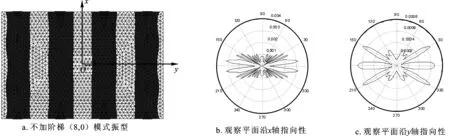
图3弯曲振动矩形板的振型和声场指向性

Fig.3The directivity diagram of a rectangular plate in flexural vibration

图4弯曲振动阶梯矩形板声场指向性

Fig.4The directivity diagram of a rectangular

plate in flexural vibration

图4a中，当观察平面沿x轴方向时，指向性图案在θ=0方向上有较尖锐的主瓣，在其他方向有较小副瓣；当观察平面垂直于矩形板表面并沿y轴方向时，指向性图案只在θ=0方向上也有尖锐的主瓣。上述方法计算得到阶梯形矩形板的辐射声场指向性。

3.2纵振激振源面激振矩形板

分别取纵振换能器激振源半径为4、8、12和16 mm，建立面激励振动模型。利用有限元计算，得到各振动模型的(8,0)模态振型图，如图5所示。

随着激振源半径的增加，(8,0)模态的共振频率逐渐增大，节线弯曲程度逐渐增大。图5a中，当激振源半径r=4 mm时，矩形薄板(8,0)模态振动节线基本呈直线，在预设阶梯位置加阶梯后图中阴影部分负相位位移基本上全都落在阶梯上而变为正值，只有小部分负相位位移落在阶梯外。当激振半径增大至r=8 mm时(图5b)，第2、3、6、7条节线弯曲程度不明显，基本为直线，第1、4、5、8条节线向外弯曲，弯曲程度较小,在预设阶梯位置加阶梯后落在阶梯外的负相位位移增多。图5c为r=12 mm时矩形板(8,0)模态振型图，可以看出，节线弯曲程度较大，第1、3、4、5、6、8条节线向外弯曲，第2、7条节线向内弯曲，负相位位移部分偏离加阶梯位置严重。图5d中，当激振半径增大到r=16 mm时，振动节线弯曲程度更加明显，第1、2、7、8条节线中间部分已经断开，第3、6条节线中间部分分别与第2、7条节线相交。随着激振源半径逐渐增大，条纹弯曲振动状态下节线偏离预设阶梯边缘位置程度增大，将处理后的位移值汇总，带入指向性程序，计算得到不同激振半径下加阶梯矩形板的指向性(如图6、图7所示)。

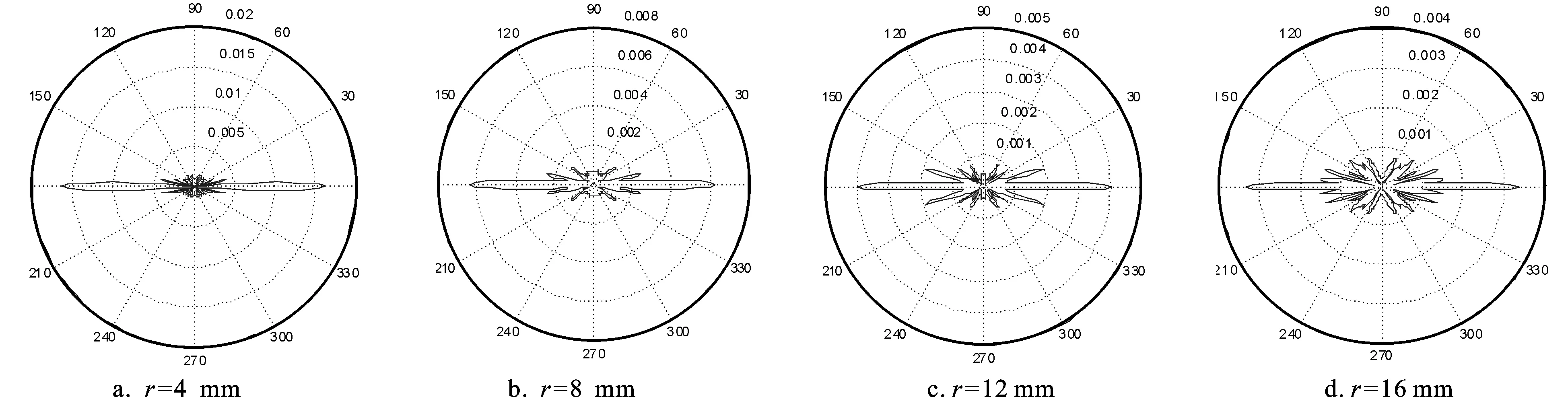
图6不同激振半径下观察平面沿x轴指向性图

Fig.6Directivity diagram with different excitation radius at observed surface along thexaxis

图6为观察平面垂直于矩形板并沿x轴，当激振源半径较小时，指向性在θ=0方向上有尖锐的主瓣，其他方向上副瓣较小，随着激振源半径逐渐增大，副瓣越来越大，声能量逐渐分散，矩形板指向性越来越差。图7为观察平面沿y轴方向，指向性尖锐程度较沿x轴时好，r≤8 mm时，观察平面沿y轴方向，指向性只有主瓣，基本没有副瓣，指向性尖锐。随着激振源半径增大，副瓣增多，指向性尖锐程度逐渐减小，当半径增大到12 mm时，副瓣已十分明显，声能量分散，指向性尖锐程度较差。对该矩形板，应选择纵振激振源半径在8 mm以内。

4结论

对于纵振换能器、变幅杆及矩形板组成的复合振动系统，本文计算了激振源变幅杆面积不同对矩形板振动特性的影响，得到如下结论：

(1)对于尺寸为(180×120×5) mm的矩形板，随着激振源面积的增加，(8,0)模态的共振频率逐渐增大。

(2)随着纵振激振源面积的逐渐增加，矩形板条纹振动节线与本征振动时的节线相比，不再为直条纹状，弯曲程度逐渐明显。激振源半径增大，节线偏离预设阶梯边缘位置程度增大，反相区域增多。

(3)面激振阶梯形矩形板，观察平面垂直于矩形板表面且沿x轴方向的指向性尖锐程度较y轴好，激振源半径增大，尖锐程度减小，当半径增大到12 mm时，副瓣较大。对该矩形板，应尽量选择激振源半径在8 mm以内。这一结果为分析面激振下阶梯形矩形板节线偏离预设阶梯位置对指向性的影响提供了参考。

参考文献:

[1] 严仁博.超声楔形换能器的体波和瑞利表面波指向性图案[J].物理学报,1974,23(6):419-428.

[2] 何正耀，马远良.水声共形阵辐射指向性计算方法及其实验验证[J].声学学报,2007,32(3):270-274.

[3] TETSURO O, BORIS A, DAVID A B. Broadband multimode baffled piezoelectric cylindrical shell transducers[J].The Journal of the Acoustical Society of America,2007,121(6):3465-3471.

[4] BORIS A,DAVID A B, COREY L B. Effects of coupledvibrations on the acoustical performance of underwater cylindrical shell transducers[J]. The Journal of the Acoustical Society of America,2007,122(6):3419-3427.

[5] 商德江，何祚镛.加肋双层圆柱壳振动声辐射数值计算分析[J].声学学报,2001,26(3):193-201.

[6] 贺西平，张频，宋旭霞．单台阶同心圆盘辐射声场的指向性计算[J].声学技术，2009，28(5):673-677．

[7] GALLEGO-JUAREZ J A, RODRIGUEZ G, ACOSTA V, et al. Power ultrasonic transducers with extensive radiators for industrial processing[J]. Ultrasonics Sonochemistry, 2010, 17: 953-964.

[8] 兰正康，贺西平，马焕培,等.阶梯圆盘节圆偏离对辐射声场指向性的影响[J].振动与冲击,2013,32(12):105-115.

[9] HE X P,YAO J,ZHANG H P,et al.Effect of excitation area of longitudinal transducer on the flexural vibration characteristics of a rectangular plate in stripe mode[J]. Ultrasonics,2015,58:104-105.

[10] CAMPOS-POZUELO C, LAVIE A, DUBUS B G.Numerical study of air-borne acoustic field of stepped-plate high-power ultrasonic transducer[J]. Acta Acustica United With Acustica,1998,84:1042-1046.

[11] 贺西平.弯曲振动阶梯圆盘辐射阻抗的计算方法[J].物理学报，2010,59(5):3290-3293.

[12] 贺西平，宋旭霞，李伟.阶梯圆盘的设计及声参数计算[J].声学学报,2010,35(5): 502-507.

[13] XIANG Y,ZHANG L.Free vibration analysis of stepped circular midline plates[J].Joural of Sound and Vibration,2005,280: 633-655.

[14] JE Y，LEE H，PARK J，et al． A stepped plate bi-frequency source for generating a difference frequency sound with aparametric array[J]．The Journal of Acoustical society of America，2010，127(6): 3494-3502．

[15] GALLEGO-JUAREZ J A，RODRIGUEZ G，RIERA-FRANCO DE S E，et al.Recent developments in vibrating-plate microsonic transducers[J]． Ultrasonics，2002，40(1/8):889-893．

[16] 姚景，贺西平.激振面积对弯振矩形板振动特性的影响[J].陕西师范大学学报(自然科学版)2014,42(2):46-49.

〔责任编辑 李博〕

Effect of longitudinal vibration excitation source area on radiated acoustic field directivity pattern of stripe vibration mode rectangular plate

LIU Doudou, HE Xiping*, LI Jiaxing

(School of Physics and Information Technology,Shaanxi Normal University, Xi′an 710119, Shaanxi, China)

Abstract:The connection between the rectangular plat and the longitudinal vibration transducer always has a certain contact area in high-power applications.Thus the deformed nodal line of stripe vibration mode don′t coincide with the expected step edge positions.Using combination of the method of numerical calculation and finite element, the influence of the excitation area on the directivity pattern in (8,0) stripe mode flexural vibration is investigated. The result shows that, for the 180×120×5 mm (length×width×thickness) rectangular plate, the nodal lines deform gradually with the increasing of excitation area.The (8,0) modal resonance frequency increases.The directivity pattern becomes less sharply and the acoustic field directivity pattern along theyaxis is sharper than that along thexaxis.When the radius of the excitation area increases to 12 mm，the side lobe is obvious.The radius of the excitation area should not be greater than 8mm for the stepped plate.Keywords: finite element method; rectangular plate; excitation area; nodal line; directivity patternPACS: 43.35.+d

文章编号：1672-4291(2016)03-0038-05

doi:10.15983/j.cnki.jsnu.2016.03.232

收稿日期：2015-03-12

基金项目：国家自然科学基金(11374201)

*通信作者：贺西平，男，教授，博士生导师。E-mail:hexiping@snnu.edu.cn

中图分类号:O426.1

文献标志码:A