广义线性模型的大样本理论及其研究进展

陈　夏， 闫　莉

(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)



广义线性模型的大样本理论及其研究进展

陈夏， 闫莉*

(陕西师范大学 数学与信息科学学院, 陕西 西安 710119)

摘要：系统介绍广义线性模型的研究概况和最新进展，主要包括广义线性模型的极大似然估计理论和拟似然估计理论、广义线性模型在复杂数据中的应用以及广义线性模型的经验似然和变量选择问题。并指出了广义线性模型将会在高维数据的理论和应用研究方面有所发展。关键词: 广义线性模型；大样本理论；拟似然方法

MR subject classification: 62J12

广义线性模型(generalized linear models, 简记为GLMs)的理论是对线性模型经典理论的重要推广，是分析不同类型数据的工具。它既适应于连续数据，也适应于离散数据，特别是后者，如计数数据和属性数据等。这在应用上，尤其是在医学、生物、经济、社会等数据的统计分析上，有重要的意义。

记Y为一维或多维的响应变量(因变量)，x为协变量(自变量)，Z=Z(x)是依赖于协变量的设计向量或设计矩阵。广义线性模型从线性回归模型的特点出发，从以下几个方面进行推广：

(1) E(Y)=μ=h(ZTβ),h为一严格单调且充分光滑的函数,β为未知的回归参数。g=h-1称为联系函数(link function)满足g(μ)=ZTβ。

(2) x,Z(x),y一般可取连续或离散值，应用上更常见的是取离散值的情形。

(3) Y的分布属于指数型，正态分布是其特例。

GLMs的起源可追溯到20世纪20年代。英国著名统计学家Fisher曾在1919年使用过它。而作为GLMs最重要特例之一的Logistic模型，Berkson、Dyke和Patterson等人在20世纪40年代就曾使用过。1972年，Nelder与Wedderburn正式引入了GLMs的概念[1]。1974年，Wedderburn研究了GLMs的拟似然方法[2]。此后，研究工作逐渐增加，GLMs成为实际数据建模的重要工具，研究成果数以万计。1983年，McCullagh和Nelder出版了系统论述GLMs的专著《Generalized linear models》并于1989年再版[3]。该书以介绍基本理论和基本方法为主，应用色彩较淡，内容广度稍显不足。1994年，Fahrmeir和Tutz出版了专著《Multivariate statistical modeling based on generalized linear models》,并于2001年再版[4]。该专著重点在于建模应用，内容面广，但较缺乏深度。两本书在理论上都着力不够，所有结果均未给出严格证明。1985年，Fahrmeir和Kaufman给出了GLMs大样本理论结果的严格证明，详细讨论了GLMs未知参数的极大似然估计的相合性和渐近正态性[5]。

笔者在武汉大学攻读博士学位期间，跟随恩师陈希孺先生系统而深入地学习了GLMs的大样本理论，并在相应的研究方向上取得了一定的进展。从2001年开始，陈先生在武汉大学主持举办了多次关于GLMs的讨论班，取得了丰富的成果。自那以后，GLMs在国内迎来了一个新的研究高潮。2002—2004年，陈希孺先生以专题讲座的形式，介绍了传统GLMs的一般理论和方法，但未给出结果的严格证明[6]。本文给出了最近30年来GLMs的研究概况和最新进展，并指出了今后可能的发展方向。

1GLMs的极大似然估计理论

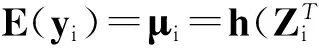
(1)

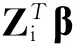
(2)

的根称为参数 的极大似然估计(maximum likelihood estimate, 简记为MLE)，这里

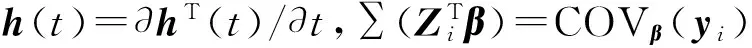
特别地，自然联系函数下的对数似然方程为

(3)

Fahrmeir和Kaufman分别在自然联系与非自然联系情形下，建立了广义线性模型参数MLE的强弱相合性和渐近正态性的一般条件,并讨论了协变量与响应变量有界的特殊情形[5]。尹长明和赵林城在去掉协变量有界的条件下，讨论了Logit模型、Probit模型和分组Cox模型等广义线性模型中MLE的相合性和渐近正态性[7]。丁洁丽和陈希孺把非自然联系和自然联系下的条件统一，研究了参数MLE的强弱相合性。另外，还研究了协变量独立但不同分布以及模型拓展的情形，对一些问题进行了理论上的完善和推广，建立了广义线性模型参数MLE大样本性质的一般理论[8-9]。Qian和Wu研究了Logistic模型下，未知参数MLE的重对数律和模型选择问题[10]。

2GLMs的极大拟似然估计理论

关于经典GLMs的统计分析,一个基本的假定是响应变量服从指数型分布。其依据是：我们的主要目的是进行离散数据的统计分析，在一些重要的情形下，这种数据的分布是二项分布、多项分布和Poisson分布等指数型分布。另外，除指数型的假定外，往往均值结构μ=h(ZTβ)的选择意味着方差有一定结构[6]。但是，在有些情况下，指数型假定不一定切合实际，且在建模时，我们往往着眼于变量的均值与方差。Wedderburn注意到在经典的GLMs中，若均值函数和方差函数已知，则很多基于似然的方法依然有效[2]。因此，拟似然方法被引入到GLMs的研究中。

注意到,一般联系函数下的似然方程(2)仅含有响应变量yi的均值函数和协方差阵(一维情形为方差函数)，而自然联系函数下的似然方程(1)仅含有yi的均值函数。这使得在不知道yi的分布是否属于指数型分布族的情形下或者总体均值和方差是否具有指数型分布族均值和方差结构的情况下，依然可以仿照标准GLMs建立拟似然方程。一般联系函数和自然联系函数下的拟似然方程分别与(2)式和(3)式有相同的形式，但不再有指数型分布的假定。基于拟似然方程(2)或(3)的解称为极大拟似然估计(maximumquasi-likelihoodestimate, 简记为MQLE)。

我们知道，与均值函数相比，有关协方差阵的确切知识更难获得。因此，Liang和Zeger为拟似然方法引入了一种更普遍的研究方法。他们提出，只要均值函数假定正确，可以预先假定响应变量的“工作分布”，进而可用“工作方差”Λ-1(·)代替真实的方差∑(·)，得到拟似然方程或广义估计方程(generalizedestimatingequation, 简记为GEE)[11]

(4)

此方法的灵活性表现在若错误地假定密度函数的形式或联系函数，还可以选择“工作分布”，且不限制响应变量的维数。而Wedderburn的拟似然方法仅适用于一维响应变量的GLMs，且选定了均值的同时也选定了“工作方差”，这可能会失去利用某些关于方差有用信息的机会。关于拟似然估计的大样本性质可参见Fahrmeir的工作[12]。

对于自然联系函数下拟似然方程(3)的研究，Chen等首次在很弱的条件下，给出了固定设计和自适应设计下，拟似然方程(3)定义的MQLE的强相合性[13]。但是，其证明的一个关键步骤有一个漏洞。据此，高启兵和吴耀华在比当前文献条件弱的情况下，利用不同的思路，分别研究了固定设计下，该MQLE的强相合性和渐近正态性[14-15]。尹长明等讨论了自适应情形下，该MQLE的渐近性质[16]。张三国和廖源以及朱春华和高启兵在较弱条件下，分别讨论了固定设计和自适应设计下MQLE的渐近存在性、弱相合性、收敛速度以及渐近正态性[17-18]。

则MQLE是强相合的，进一步加上相应的矩条件，MQLE也是渐近正态的[23]。Xiao和Liu讨论了GLMs中MQLE的重对数律问题[24]。

在估计方程(4)中，一般要指定一个函数充当协差阵或方差函数的角色，这在一定程度上扩大了应用范围，但若选择不当可能会造成效率的降低。因此，Chiou和Müller利用非参数方法对方差函数进行估计，证明所得MQLE有相合性和渐近正态性，且其极限分布的协差阵与使用正确方差函数所得估计的极限分布的协差阵相同，即可能达到了最好的情况[25]。该结果是一个实质的进展，它提供了一种方法，可以在方差函数完全未知的情形下给出参数的估计，其效果与方差函数已知时所能达到的效果相同。但是，文献[24]在定义MQLE时存在一定的问题，导致后续的证明及结论尚存可疑之处。陈夏和陈希孺对其定义的估计进行了修改，对修改后的估计量证明了上述结果[26]。另外，Chiou和Müller利用局部线性加权的方差函数估计方法，得到了GLMs中方差函数估计的收敛速度，其至多达到Op(n-1/3)[25]。陈夏利用局部多项式加权的方法以及细节上的处理，改进了收敛区间，并把收敛速度提高为可任意接近Op(n-1/2)[27]。

3基于复杂数据的GLMs研究

在实际应用中，我们经常见到诸如纵向数据和缺失数据等复杂数据类型。基于复杂数据的GLMs建模，在生物医学、经济金融等领域的应用也很广泛。例如，Liang和Zeger提出了基于纵向数据的GLMs中的广义估计方程研究方法[11]。在数据缺失时，Wang等结合逆概率加权方法研究了GLMs中的局部线性回归估计[28]。Ibrahim等研究了标准GLMs(响应变量服从指数型分布)中处理数据缺失的几种方法[29]。Chen等考虑了非参数形式下GLMs中的响应变量均值的局部拟似然借补估计[30]。闫莉和陈夏讨论了响应变量随机缺失时，GLMs拟似然估计的渐近存在性、强相合性和收敛速度[31]。赵晶晶等讨论了协变量缺失时，GLMs拟似然估计的相合性和渐近正态性[32]。肖枝洪和刘禄勤研究了不完全信息随机截尾的GLMs的极大似然估计的渐近性质[33-34]。下面我们以缺失数据为例，简单讨论一下GLMs的建模过程和研究方法。

考虑以h为联系函数的广义线性模型，即响应变量yi∈R和设计向量Zi∈Rp满足

(5)

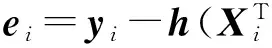
在响应变量yi有缺失的情形下，即在模型(5)中得到了不完全样本{(yi,Zi,δi):1≤i≤n}，其中Zi可以观测，若yi缺失，则δi=0，否则δi=1。这里假定yi是随机缺失(missing at random, 简记为MAR)的情形，即选择概率为

P(δi=1|yi,Zi)=P(δi=1|Zi)=p(Zi)。

(6)

仿照拟似然方程(3)，可以建立基于完全数据(complete case, 简记为CC)方法的拟似然方程

(7)

另外，还可构造基于加权方法的拟似然方程为

(8)

作为yi的完全数据集。若p(·)未知，可用其估计量代替。基于此完全数据集的拟似然方程为

(9)

4GLMs的经验似然与变量选择

基于经验似然的统计分析是近年统计学的热点研究课题。自经验似然方法由Owen提出以来[35]，因其在构造参数置信域方面有众多突出的优点，例如，无需对渐近方差进行估计、置信域的形状由数据自行决定、域保持性、Bartlett纠偏性等，被许多研究者应用到处理各种数据的问题。变量选择问题也是近年统计学的前沿和热点研究方向。在实际问题中，如在基因学中，实验者可能只有几百人，而观测到的基因位点(变量)可能有几千上万个。研究者要通过较少的样本选取与某种疾病相关的基因。因此，变量选择在高维数据分析中发挥着重要作用。

基于模型(5)和拟似然方程(3)，引入辅助随机向量

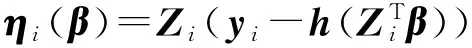
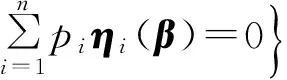
(10)

由拉格朗日乘数法，知

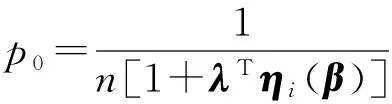
(11)

ln(β)可表示为

(12)

这里λ=λ(β)满足

(13)

在适当的条件下，可证明经验对数似然比函数ln(β0)渐近于标准卡方分布，因此该统计量可用于构造未知参数的置信区域和假设检验等问题。在GLMs的经验似然研究方面，Kolaczyk基于拟似然函数方法中的得分函数，把经验似然方法引入到广义线性模型中[36]。Chen和Cui利用广义线性模型中方差函数的结构提出了一种改进的经验似然方法[37]。闫莉和陈夏在固定和自适应设计情形下，利用拟似然方法研究了GLMs的经验似然推断问题，证明了经验对数似然比统计量ln(β0)渐近于标准卡方分布，因此可直接用于统计推断[38]。Xue等在数据缺失下，利用拟似然函数方法，研究了方差函数已知时，GLMs的经验似然推断，但未涉及方差函数未知或研究拟似然方程的情况[39]。闫莉和陈夏在响应变量随机缺失下，利用完全数据方法、加权方法和借补方法结合拟似然方程法讨论了GLMs的经验似然推断[40-41]。

基于惩罚函数的变量选择方法，是当前较为流行的可以较好处理高维模型选择的方法。它可以同时实现变量选择和参数估计，这大大提高了计算速度。该方法通过最小化惩罚目标函数来进行变量选择，目标函数由损失函数和惩罚项构成。

在GLMs的变量选择研究方面，Meier等讨论了高维Logistic回归下的Group LASSO方法[42]。van de Geer基于Lipschitz损失和LASSO惩罚，研究了GLMs中估计的预测误差[43]。Fan和Song基于极大边际似然估计提出了超高维GLMs的独立筛选方法[44]。Friedman等基于Elastic Net惩罚讨论了GLMs中估计的快速算法问题[45]。Fan和Lv在超高维情形下研究了GLMs基于非凹惩罚似然的变量选择方法[46]。Wang等利用Adaptive LASSO方法，研究了高维GLMs的变量选择和参数估计问题，并得到了估计的Oracle性质[47]。Jiang和Huang基于凹惩罚似然，讨论了高维GLMs中的MMCD算法[48]。

5结论

本文从GLMs的大样本理论出发，给出了近年来国内外关于GLMs极大似然估计理论、极大拟似然估计理论、经验似然、变量选择以及GLMs在复杂数据中的应用等问题的研究现状和研究进展。

近年来，高维数据的统计分析极大地推进了统计思想的改革与发展，成为当代统计的研究热点，出现了一大批令人瞩目的研究成果[49-50]。因此，今后GLMs的发展方向，将会集中在高维数据的理论和应用研究方面。例如，研究高维GLMs的降维、模型和变量选择、经验似然推断以及假设检验等问题。

2015年正值恩师陈希孺先生逝世十周年,先生的谆谆教诲和殷切希望犹在耳边。作者谨以此文纪念先生，表达我们深切的缅怀之情。

参考文献：

[1] NELDER J A, WEDDERBURN R W M. Generalized linear models[J]. Journal of the Royal Statistical Society: Series A, 1972, 135(3): 370-384.

[2] WEDDERBURN R W M. Quasi-likelihood functions, generalized linear models and Gauss-Newton method[J]. Biometrika, 1974, 61(3): 439-447.

[3] McCULLAGH P, NELDER J A. Generalized linear models[M].2nd ed. London:Chapman & Hall,1989.

[4] FAHRMEIR L, TUTZ G. Multivariate statistical modelling based on generalized linear models[M]. 2nd ed.New York:Springer-Verlag, 2001.

[5] FAHRMEIR L, KAUFMANN H. Consistency and asymptotic normality of the maximum likelihood estimator in generalized linear models[J]. The Annals of Statistics, 1985, 13: 342-368.

[6] 陈希孺. 广义线性模型(一)[J].数理统计与管理, 2002,21(5):54-61.

[7] 尹长明, 赵林城. 广义线性模型极大似然估计的强相合性与渐近正态性[J]. 应用概率统计, 2005, 21(3): 249-260.

[8] DING J L, CHEN X R. Asymptotic properties of the maximum likelihood estimate in generalized linear models with stochastic regressors[J]. Acta Mathematica Sinica: English Series, 2006, 22(6): 1679-1686.

[9] 丁洁丽, 陈希孺. 广义线性回归极大似然估计的强相合性[J]. 数学物理学报, 2006, 26A(2): 168-173.

[10] QIAN W, WU Y H. Strong limit theorems on model selection in generalized linear regression with binomial responses[J]. Statistica Sinica, 2006, 16: 1335-1365.

[11] LIANG K Y, ZEGER S. Longitudinal data analysis using generalized linear models[J]. Biometrika, 1986, 73: 13-22.

[12] FAHRMEIR L. Maximum likelihood estimation in misspecified generalized linear models[J]. Statistics, 1990, 21: 487-502.

[13] CHEN K, HU Y, YING Z. Strong consistency of maximum quasi-likelihood estimators in generalized linear models with fixed and adaptive designs[J]. The Annals of Statistics, 1999, 27(4): 1155-1163.

[14] 高启兵, 吴耀华. 广义线性回归拟似然估计的强相合性[J]. 数学年刊, 2004, 25A(6):705-710.

[15] 高启兵, 吴耀华. 广义线性回归拟似然估计的渐近正态性[J] . 系统科学与数学, 2005,25(6):738-745.

[16] 尹长明, 韦程东, 刘小红.自适应设计广义线性模型极大拟似然估计的渐近性[J]. 高校应用数学学报, 2008, 23(2): 207-212.

[17] ZHANG S G, LIAO Y. On some problems of weak consistency of quasi-maximum likelihood estimates in generalized linear models[J]. Science China Mathematics, 2008, 51(7): 1287-1296.

[18] ZHU C H, GAO Q B. Asymptotic properties in generalized linear models with natural link function and adaptive designs[J]. Adavances in Mathematics, 2013, 42(1): 121-127.

[19] 岳丽, 陈希孺. 广义线性模型中拟极大似然估计的强相合性及收敛速度[J]. 中国科学(A辑), 2004, 34 (2): 203-214.

[20] 赵林城, 尹长明. 广义线性模型中极大拟似然估计的强相合性[J]. 中国科学(A辑), 2005, 35 (3): 312-317.

[21] CHANG Y I. Strong consistency of maximum quasi-likelihood estimate in generalized linear models via a last time[J]. Statistics and Probability Letters, 1999, 45: 237-246.

[22] YUE L, CHEN X R. Asymptotic normality of quasi-maximum likelihood estimate in generalized linear models[J]. Chinese Annals of Mathematics, 2005, 26(3): 467-474.

[23] 尹长明, 赵林城. 广义线性模型中极大拟似然估计的渐近正态性和强相合性[J]. 中国科学(A辑), 2005, 35(11): 1236-1250.

[24] XIAO Z H, LIU L Q. Laws of iterated logarithm for quasi-maximum likelihood estimator in generalized Linear model[J]. Journal of Statistical Planning and Inference, 2008, 138(3): 611-617.

[25] CHIOU J M , MÜLLER H G. Nonparametric quasi-likelihood[J]. The Annals of Statistics, 1999, 27,36-64.

[26] 陈夏, 陈希孺. 广义线性模型参数的自适应拟似然估计[J]. 中国科学(A辑), 2005, 35(4): 463-480.

[27] 陈夏. 广义线性模型中方差函数的非参数估计[J]. 应用概率统计, 2006, 22(4): 337-346.

[28] WANG C Y, WANG S, GUTIERREZ R G, et al. Local linear regression for generalized linear models with missing data[J]. The Annals of Statistics, 1998, 26: 1028-1050.

[29] IBRAHIM J G, CHEN M H, LIPSITZ S R, et al. Missing-data methods for generalized linear models: a comparative review[J]. Journal of the American Statistical Association, 2005, 100(469): 332-346.

[30] CHEN J W, FAN J, LI K H, et al. Local quasi-likelihood estimation with data missing at random[J]. Statistica Sinica, 2006, 16: 1071-1100.

[31] 闫莉, 陈夏. 缺失数据下广义线性回归拟似然估计的强相合性[J]. 陕西师范大学学报(自然科学版), 2010, 38(2): 15-17.

[32] 赵晶晶, 张晓冉, 徐玉民.缺失数据下广义线性回归拟似然估计的相合性和渐近正态性[J]. 郑州大学学报(理学版), 2011, 43(3): 43-47.

[33] 肖枝洪, 刘禄勤. 不完全信息随机截尾广义线性模型的极大似然估计[J]. 数学物理学报, 2008, 28A(3): 553-564.

[34] XIAO Z H, LIU L Q. Laws of iterated logarithm for MLE of generalized linear model randomly censored with incomplete information[J]. Statistics and Probability Letters, 2009, 79(6): 789-796.

[35] OWEN A B. Empirical likelihood ratio confidence intervals for a single function[J]. Biometrika, 1988, 75: 237-325.

[36] KOLACZYK E D. Empirical likelihood for generalized linear models[J]. Statistica Sinica, 1994, 4: 199-218.

[37] CHEN S X, CUI H J. An extended empirical likelihood for generalized linear models[J]. Statistica Sinica, 2003, 13: 69-81.

[38] YAN L, CHEN X. Empirical likelihood for generalized linear models with fixed and adaptive designs[J]. Statistics, 2015, 49(5): 978-988.

[39] XUE D, XUE L G, CHENG W H. Empirical likelihood for generalized linear models with missing responses[J]. Journal of Statistical Planning and Inference, 2011, 141: 2007-2020.

[40] 闫莉, 陈夏. 缺失数据下广义线性模型的经验似然推断[J]. 统计与信息论坛, 2013, 28(2): 14-17.

[41] 闫莉, 陈夏. 响应变量随机缺失下广义线性模型的经验似然[J]. 陕西师范大学学报(自然科学版), 2015, 43(3): 1-5.

[42] MEIER L, van de GEER S, BÜHLMANN P. The group LASSO for logistic regression[J]. Journal of the Royal Statistical Society: Series B, 2008, 70: 53-71.

[43] van de GEER S. High-dimensional generalized linear models and the LASSO[J]. The Annals of Statistics, 2008, 36: 614-645.

[44]FANJ,SONGR.SureindependencescreeningingeneralizedlinearmodelswithNP-dimensionality[J].TheAnnalsofStatistics, 2010, 38: 3567-3604.

[45]FRIEDMANJ,HASTIET,TIBSHIRANIR.Regularizationpathsforgeneralizedlinearmodelsviacoordinatedescent[J].JournalofStatisticalSoftware, 2010, 33(1): 1-22.

[46]FANJ,LVJ.Non-concavepenalizedlikelihoodwithNPdimensionality[J].IEEETransactionsonInformationTheory, 2011, 57: 5467-5484.

[47]WANGMQ,WANGXL.AdaptiveLassoestimatorsforultrahighdimensionalgeneralizedlinearmodels[J].StatisticsandProbabilityLetters, 2014, 89: 41-50.

[48]JIANGDF,HUANGJ.Majorizationminimizationbycoordinatedescentforconcavepenalizedgeneralizedlinearmodels[J].StatisticsandComputing, 2014, 24: 871-883.

[49]FANJ,HANF,LIUH.Challengesofbigdataanalysis[J].NationalScienceReview, 2014, 1: 293-314.

[50]BÜHLMANNP,vandeGEERS.Statisticsforhigh-dimensionaldata:methods,theoryandapplications[M].Heidelberg:Springer, 2011.

〔责任编辑宋轶文〕

Progress and large sample theory of generalized linear models

CHEN Xia, YAN Li*

(School of Mathematics and Information Science, Shaanxi Normal University,Xi′an 710119, Shaanxi, China)

Keywords:generalized linear models; large sample theory; quasi-likelihood method

Abstract:A comprehensive review and the latest progress of the generalized linear models is studied, including the maximum likelihood estimate theory and the maximum quasi-likelihood estimate theory of generalized linear models, its application with complicated data, the empirical likelihood and variable selection in generalized linear models. At last, it is noted that the future possible research areas will be in the theory and application of high dimension data.

文章编号：1672-4291(2016)03-0001-06

doi:10.15983/j.cnki.jsnu.2016.03.131

收稿日期：2015-07-04

基金项目：国家自然科学基金(11201276)；陕西省自然科学基础研究计划(2014JQ1042)；中央高校基本科研业务费专项资金(GK201503012, GK201503015)

*通信作者:闫莉，女，讲师，博士。E-mail:lyan@snnu.edu.cn

中图分类号：O212.1

文献标志码：A