基于RQI分类利用毛管压力曲线计算原始含油饱和度

黄　成，张爱琴，王晓畅，宋秋强，李　权

(1.长江大学 地球物理与石油资源学院，湖北 武汉　430100；2.中国石油化工股份有限公司 石油勘探开发研究院，北京　100083；3.塔里木油田勘探开发研究院，新疆 库尔勒　841000)

基于RQI分类利用毛管压力曲线计算原始含油饱和度

黄成1，张爱琴2*，王晓畅2，宋秋强3，李权1

(1.长江大学 地球物理与石油资源学院，湖北 武汉430100；2.中国石油化工股份有限公司 石油勘探开发研究院，北京100083；3.塔里木油田勘探开发研究院，新疆 库尔勒841000)

摘要：储层原始含油饱和度是评价储层的重要参数，一般是通过压汞资料得到的毛管压力曲线来求取该参数。然而，在具有相同进驱力时，微观孔隙结构对含油饱和度的影响起到了非常大的作用；同时，通过理论分析所得，储层品质指数是定量表征储层微观孔隙结构的最佳宏观物性参数。研究基于储层品质指数对岩心分析数据进行分类，进而利用毛管压力曲线求取储层原始含油饱和度，最终应用于其它储层。

关键词：储层品质指数；毛管压力曲线；分类计算；原始含油饱和度

0引言

利用毛管压力曲线计算储层原始含油饱和度一直是求取该参数的基本方法之一，然而不同微观孔隙结构的储层在相同的进驱力的情况下其含油饱和度有很大的差别，且只能在取心处利用压汞资料获取毛管压力曲线。因此，通常测井分析利用储层品质指数、流动单元或者J函数法将有限的毛管压力曲线资料进行分类[1-3]，找出常规测井曲线与其之间的数学关系，从而应用于其它储层。

研究基于储层品质系数将岩心分析的压汞资料分为3个类别，发现声波曲线及密度曲线与储层品质系数之间存在良好的对应关系，故先利用声波曲线和密度曲线将储层进行分类；然后，对应不同的储层类别，拟合出相应的原始含油饱和度计算公式，将其应用于其它储层，取得了较好的效果。

1基于储层品质指数的分类

储层物性参数主要为孔隙度、渗透率及它们的各种不同组合，例如储层品质指数(RQI)、地层流动带指数(FZI)等。储层的物性参数能够反映储层的储集渗流能力，间接反映储层孔隙结构，用于划分岩石物理相。

方法在孔隙空间为毛管束的假设条件下，给出了渗透率的经典表达式：

(1)

(1)式中：K为渗透率，单位为10-3μm2；φe为有效孔隙度，单位为%；Fs为形状因子，无量纲；τ表示弯曲度，无量纲；Sgv为单位骨架体积的孔隙表面积，单位为μm-1；Fsτ2称为Kozeny常数。利用储层品质指数与渗透率之间的关系，得出了其定义式：

(2)

由储层品质系数的定义式不难看出，该参数能在很大程度上反应储层孔隙结构的品质[6]。

利用储层品质指数对国外某油田3口井90块岩样分析数据做统计分类如图1和图2；

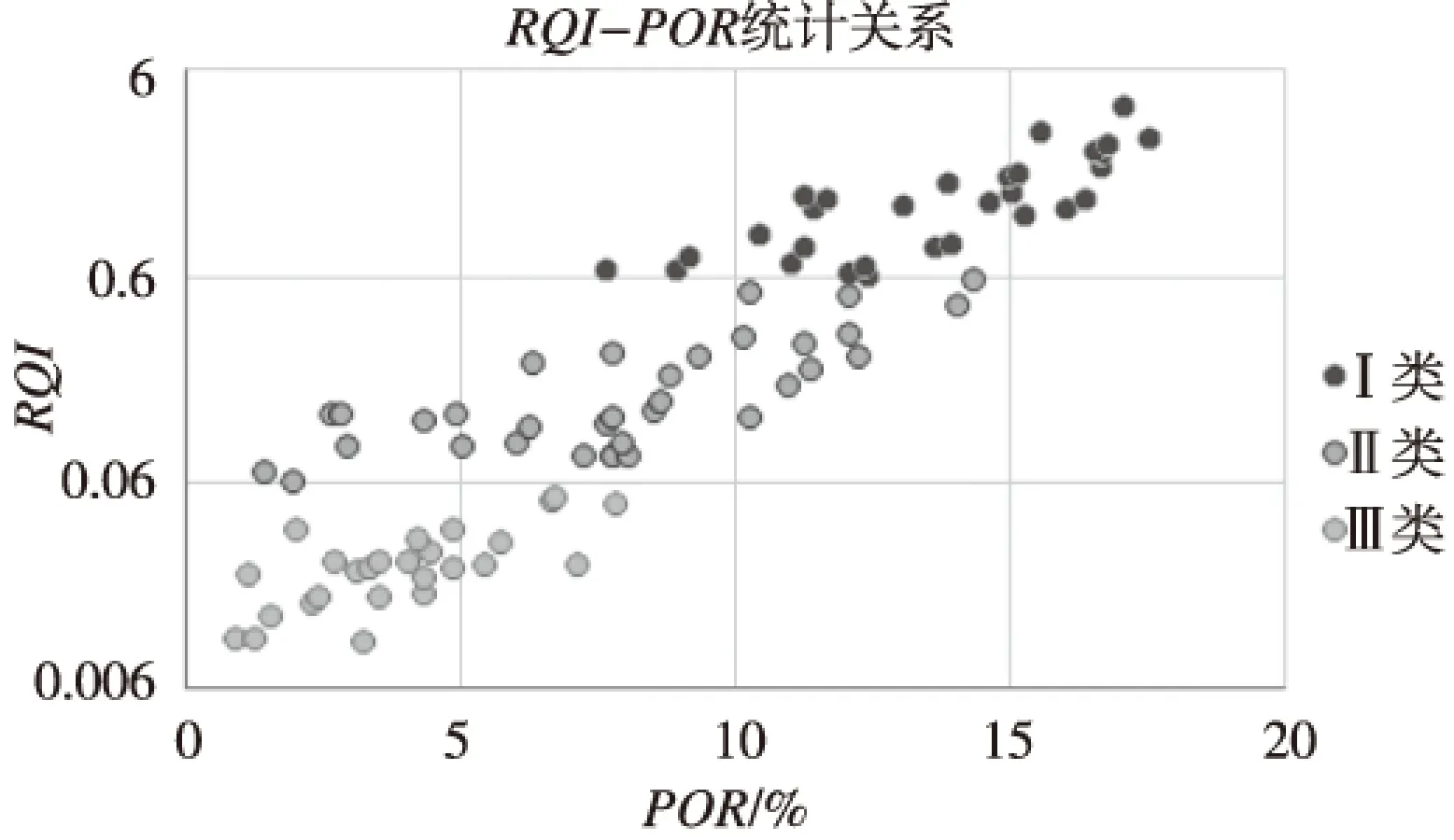
图1　储层品质指数分类Fig.1　RQI Classification

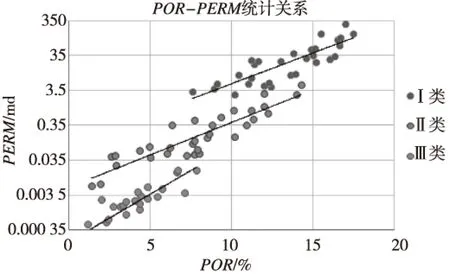
图2　岩心分类后的孔-渗关系Fig.2　Relationship of Core Por-Perm analysis

图1中储层品质指数分类标准及图2中3类孔-渗关系式如表1：

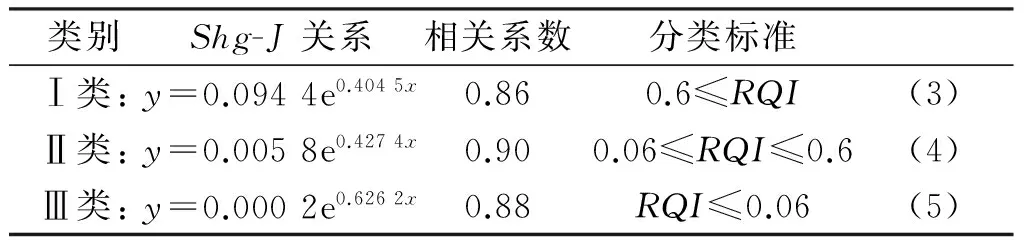
表1　RQI分类标准及孔-渗关系

当岩心不分类时，y=0.000 3e0.790 1x，相关系数R=0.80，从上述分析可知，利用储层品质指数分类后，孔-渗关系变好，同时，为了让该分类方法能够利用到其它储层，故找出常规测井曲线与储层品质指数之间的关系如下表[4，5]：

表2　RQI与常规曲线关系

表2中，PORD为密度曲线在体积模型下计算的总孔隙度，v/v；PORA为声波时差曲线在体积模型下计算的总孔隙度，v/v；CNL为中子曲线；v/v。由分析可知，RQI与密度曲线和声波曲线的二元回归关系较好，故该研究采用该方法来划分储层类型。

2分类计算原始含油饱和度

2.1J函数与进汞饱和度关系的建立

J函数数学模型的提出是为了消除渗透率和饱和度的影响，同时解决取平均值和综合对比研究的问题[4]。其表达式如下：

(6)

式中式pc为进汞压力，θL为实验室条件下的润湿角(°)，σL为实验室条件下的界面张力(mN/m)，K为渗透率(μm2)，Ф为孔隙度(%)[6,7]。

利用压汞资料计算的J函数值与实验进汞饱和度Shg建立关系如下：

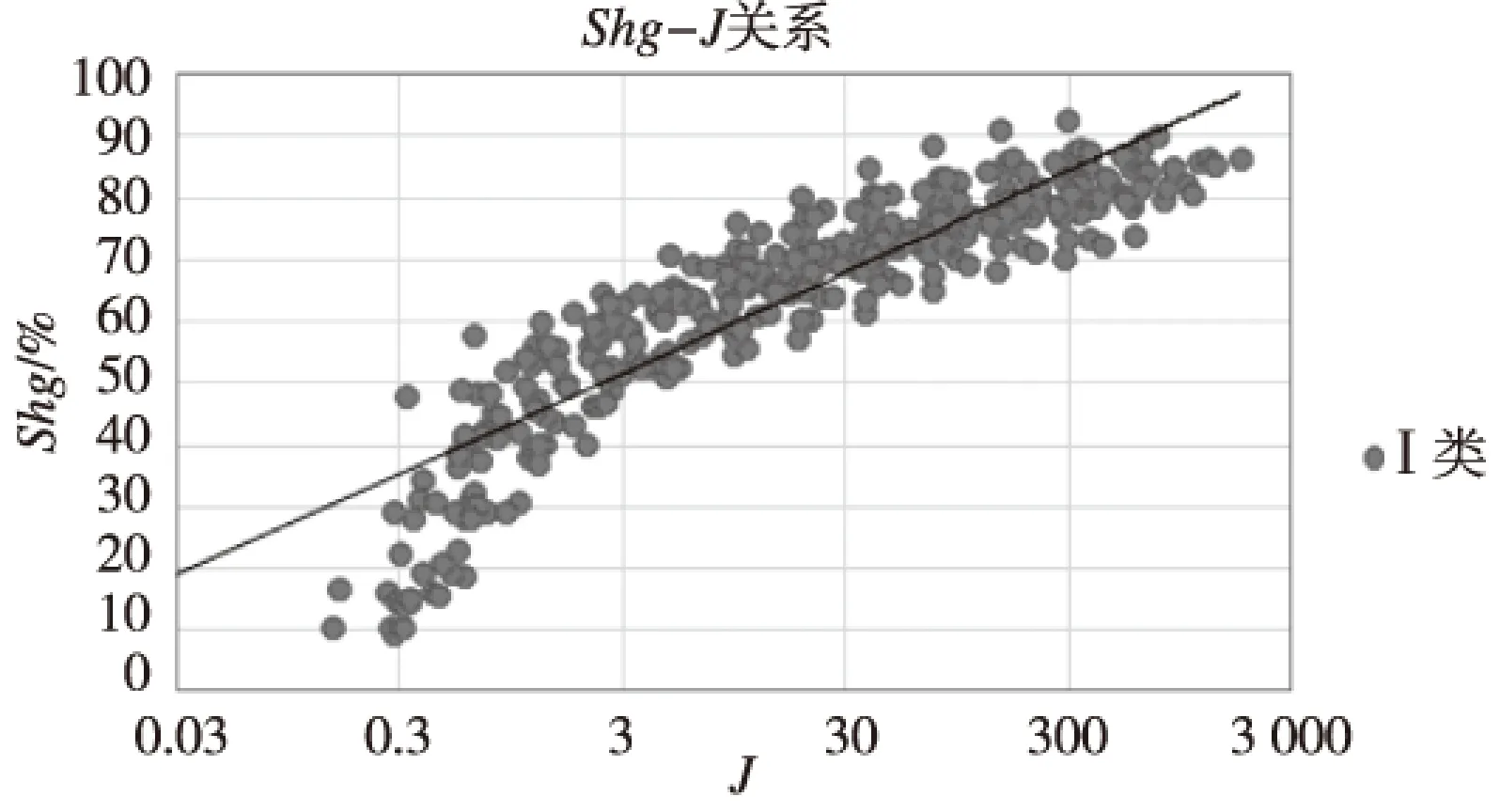
图3　Ⅰ类Shg-J关系Fig.3　Shg-J relationship of I

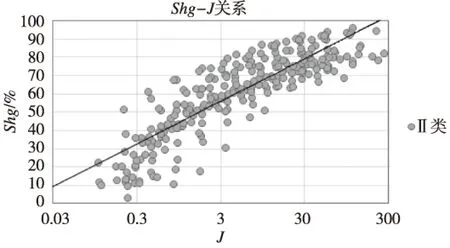
图4　Ⅱ类Shg-J关系Fig.4　Shg-J relationship of II

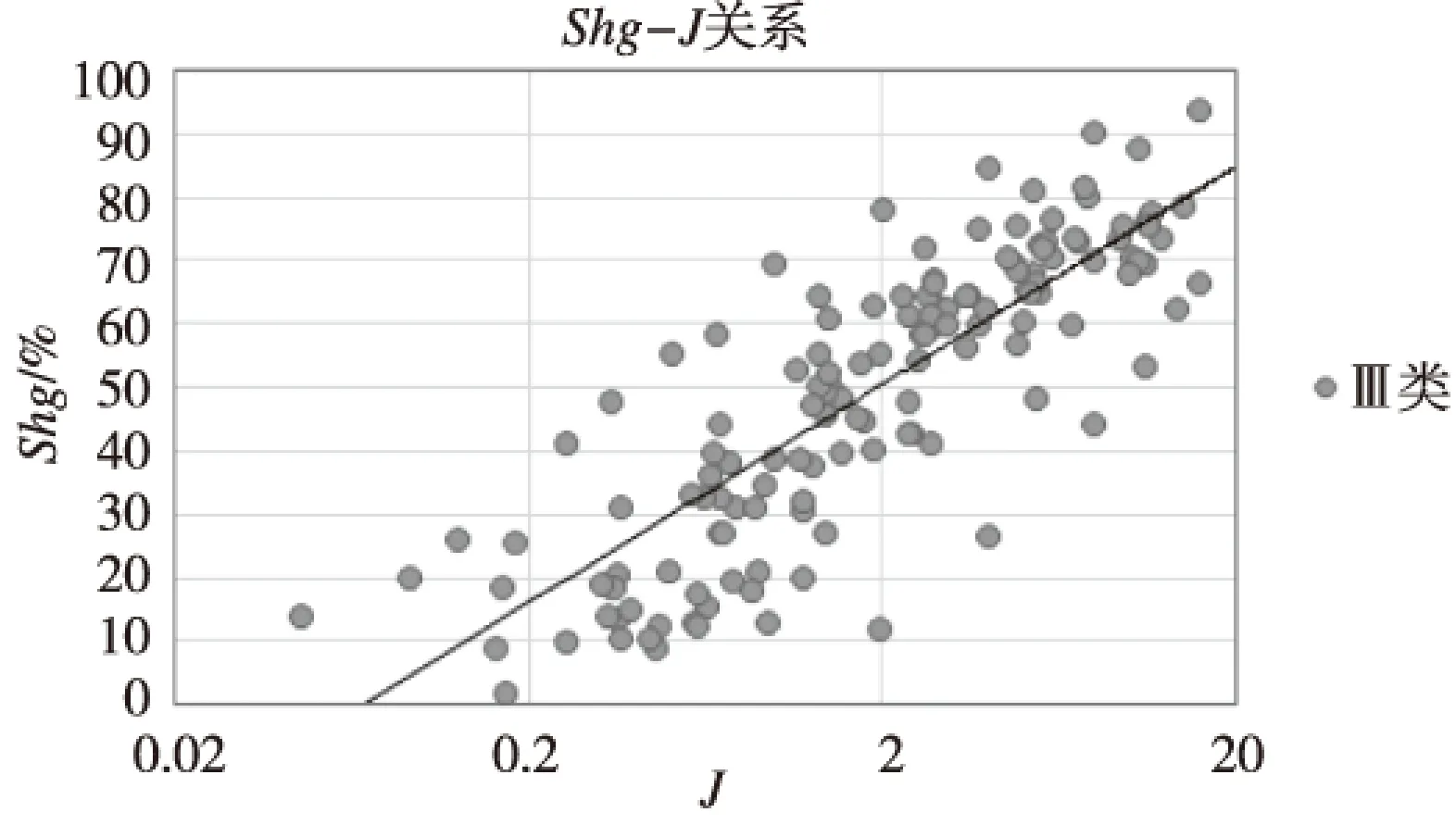
图5　Ⅲ类Shg-J关系Fig.5　Shg-J relationship of III

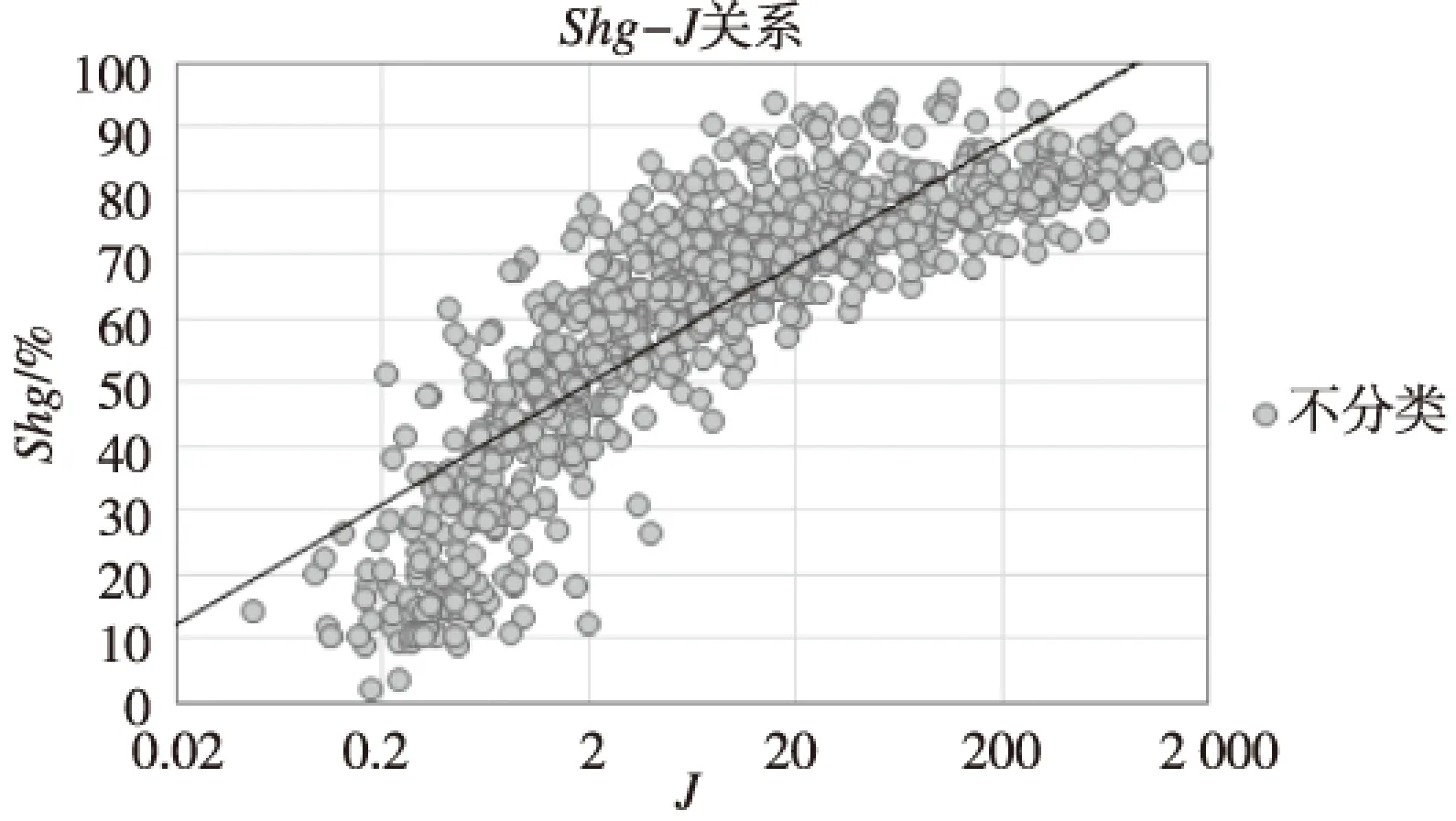
图6　不分类Shg-J关系Fig.6　Shg-J relationship of all points

类别Shg-J关系相关系数I类y=7.084ln(x)+43.9790.90II类y=10.095ln(x)+44.8410.86III类y=14.894ln(x)+40.2340.84不分类y=8.194ln(x)+44.0950.83

2.2实验室条件与地层条件之间的压力转换

式(6)中的pc为实验室条件下的毛管压力，而实际计算中用到的为地层条件下的毛管压力，故我们需要将两种毛管压力进行转换，具体转换关系如下。

实验室毛管压力与地层毛管压力可以用以下公式表示：

pCR=σRcosθR

(7)

pCL=σLcosθL

(8)

式中θL、θR分别为实验室和地层条件下的润湿角(o)，σL、σR分别为实验室和地层条件下的界面张力(mN/m)，pCR、pCL分别为实验室和地层条件下的毛管压力(MPa)。故实验室和地层条件下的毛管压力之间的关系可用下式表示：

(9)

根据美国岩心公司提供的资料，将不同系统的σ和θ值列于下表。

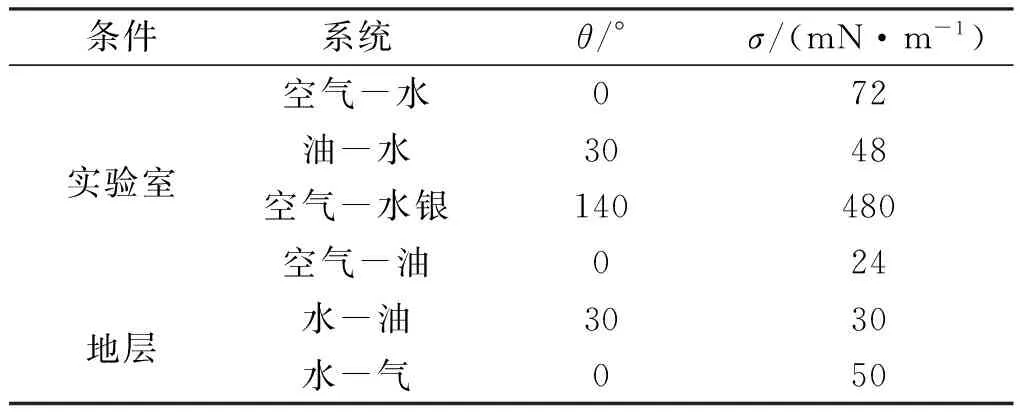
表4　不同系统中的σ和θ值

pCR与含油高度之间地层条件下油水密度的关系为：

pCR= ((ho-w-h)(ρw-ρo)g)/1 000

(10)

式中ρw、ρo分别为地层水和地层原油的密度(g/cm3)，ho-w为油水界面高度，g为重力加速度，一般取值为9.8m/s2。

故联立式(6)-(10)可知，原始含油饱和度So是关于含油高度、地层水密度、地层原油密度的函数，即So=f(ρw、ρo、ho-w)。只要知道这3个参数，即可求出原始含油饱和度[8]。利用RQI分类前后的公式计算的含油饱和度与密闭取心分析作对比，如图7所示：

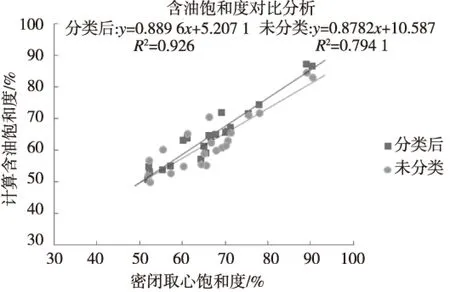
图7　计算与实验分析含油饱和度对比Fig.7　The contrast of oil saturation by computation and experimental analysis

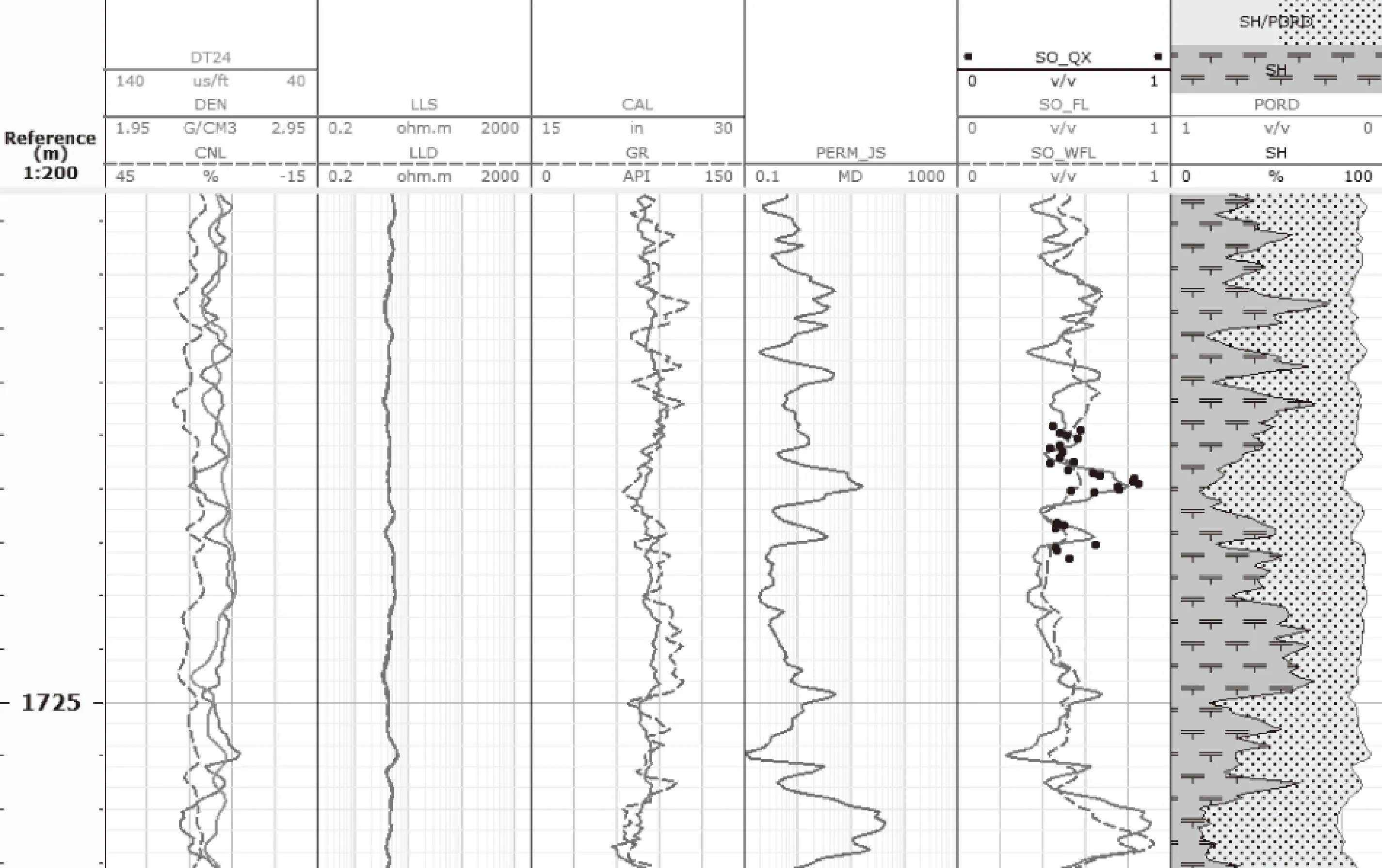
图8　 XX井RQI分类前后含油饱和度计算对比图Fig.8　The comparison figure of oil saturation by the classification of RQI

图8中，So_QX是密闭取心数据，So_FL是分类后的含油饱和度曲线，So_WFL是分类前的含油饱和度曲线，由图可知，先将储层进行分类，然后计算含油饱和度，所得结果的精度相较于未分类时有了明显的提高。

3结论

1)储层品质指数能够将不同孔喉结构的储层区分出来，通过利用储层品质指数将岩心实验数据的孔渗关系分为了3个类别，提高了渗透率的计算效果，同时与常规测井曲线结合起来，应用于全井段，取得了不错的分类效果。

2)经过储层分类后，利用毛管压力曲线计算得到的储层原始含油饱和度的精度相较分类前得到了明显的提高。

参考文献：

[1] 潘和平,樊政军.储层原始含油饱和度计算方法研究[J].现代地质,2000,14(4):451-453.

[2] 马旭鹏.储层物性参数与其微观孔隙结构的内在联系[J].勘探地球物理进展,2010,33(3):216-219.

[3] 肖亮,梁晓东,林雨静.储层原始含油饱和度评价新方法研究[J].石油地质与工程,2008,21(6):53-55.

[4] 范卫东,刘海东.塔河油田石炭系测井曲线特征和物性特征[J].工程地球物理学报,2006,3(5):350-353.

[5] 袁秀婷.新疆塔河石炭系油气储层测井最优化评价[J].工程地球物理学报,2004,1(6):513-519.

[6] 廖敬,彭彩珍,吕文均,等.毛管压力曲线平均化及J函数处理[J].特种油气藏,2008,15(6):73-75.

[7] 胡勇,于兴河,陈恭洋,等.平均毛管压力函数分类及其在流体饱和度计算中的应用[J].石油勘探与开发,2012,39(6):733-738.

[8] 张程恩,潘保芝,刘倩茹.储层品质因子RQI结合聚类算法进行储层分类评价研究[J].国外测井技术,2012(4):11-13.

Original oil saturation is calculated by capillary pressure curve which is based on the classification ofRQI

HUANG Cheng1,ZHANG Aiqin2*,WANG Xiaochang2,SONG Qiuqiang3,LI Quan1

(1.Geophysics and Petroleum Resources,Yangtze University,Wuhan,Hubei 430100,China;2.Research Institute of Petroleum Exploration and Development,SINOPEC,Beijing 100083,China;3.Exploration and Development Institute,Tarim Oilfield, Korla,Xinjiang 841000,China)

Abstract:The original reservoir oil saturation is an important parameter to evaluate reservoir. We can strike it through the use of mercury capillary pressure curve calculation. However, with the same force into the drive, the influence of microscopic pore structure on oil saturation has played a very important role; at the same time, proceeds through theoretical analysis, reservoir quality index is the best macroscopic properties parameters to quantitative characterization of reservoir microscopic pore structure. So this article based on reservoir quality index to classify routine core analysis data, and thus the use of capillary pressure curve to compute the original reservoir oil saturation, then applies to the other reservoirs.

Key words:reservoir quality; mercury capillary pressure curve; classification calculation; original reservoir oil saturation

文章编号：1004—5570(2016)02-0093-04

收稿日期：2015-11-10

作者简介：黄成(1991-)，男，硕士研究生，研究方向：测井资料解释，E-mail：353204067@qq.com. *通讯作者：张爱琴(1970-)，女，硕士，高级工程师，研究方向：测井资料处理及解释，E-mail：854928091@qq.com.

中图分类号：P618.13

文献标识码：A