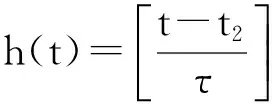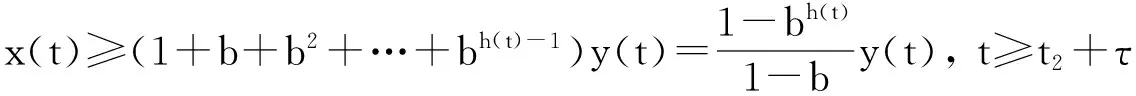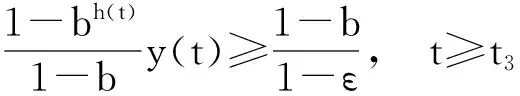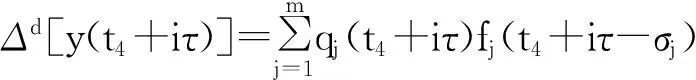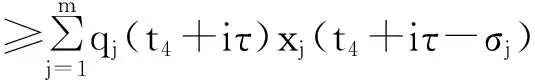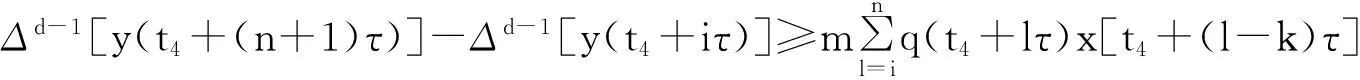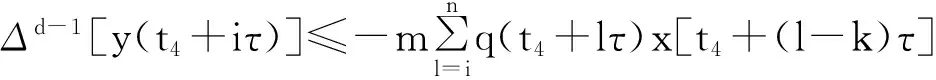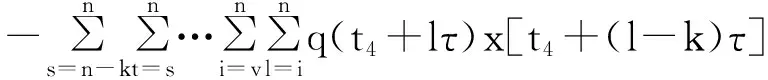具连续变量的高阶非线性差分方程的有界振动
2016-06-20杨禹慧赵良鹏
杨禹慧,赵良鹏
(1.吕梁学院 数学系,山西 吕梁 033000;2.山西大学 数学科学学院,山西 太原 030006)
具连续变量的高阶非线性差分方程的有界振动
杨禹慧1,赵良鹏2*
(1.吕梁学院 数学系,山西 吕梁033000;2.山西大学 数学科学学院,山西 太原030006)
摘要:利用一些分析技巧,研究了一类具有连续变量的高阶非线性差分方程的有界解的振动性,给出了有界解振动的充分条件。
关键词:差分方程;有界解;振动;最终正解
0引言
由于差分方程理论在自然学科和边缘学科的迅速发展,并且差分方程作为离散系统与相应的连续系统具有一些不同的特性,因此对离散系统定性理论的研究是非常有意义的。
这些年来,关于具有连续变量的高阶中立型时滞差分方程振动性的研究也有了一些结果,另外,关于具有连续变量的高阶差分方程的有界振动的研究,可见文献[1-4]; 带有强迫项的高阶差分方程解的振动性的研究可见文献[5]。
在文献[4]中,杨甲山等研究了具有连续变量的高阶中立型时滞差分方程,即
的解的振动性,其中d为奇数,本文在此基础上重新对d进行设定,用新的方法研究一类更为广泛的具有连续变量的高阶非线性差分方程即
(1)
的解的振动性。其中,d为正整数,σj≥0是给定的正数;b≤b(t)<1,(0≤b<1); 这里假设(H0):qj(t)∈([t0,+∞),+),j=1,2,…m,且qj(t)为不恒为0的有界函数, 其中fj(t)∈(,),,且函数fj(x)单调非减。τ,t0是给定的非负实数,σ=kτ,k为某个正整数;Δx(t)=x(t+τ)-x(t),Δ2x(t)=Δ(Δx(t))。 我们总假设方程(1)存在解。方程(1)的一个有界解{x(t)}称为最终正的是指当t(t>t0)充分大时,有x(t)>0,则该解为非振动的,否则是振动的。若方程(1)的每一个有界解{x(t)}都是振动的,称该方程为振动的。
1基本引理
引理1[6]假设d≥1是整数,{z(t+nτ)}是实数列,如果{Δdz(t+nτ)}最终定号(即当n充分大后恒有{Δdz(t+nτ)}>0或有{Δdz(t+nτ)}<0),则{Δiz(t+nτ)}最终严格单调且定号(i=0,1,2,…d-1)。
引理2[7]设z(n)>0(n≥a),Δpz(n)(n≥a)定号且不为0,则存在整数j(0≤j≤p),对于Δpz(n)≤0,p+j为奇数;对于Δpz(n)≥0,p+j为偶数。使对n≥a有: (a)若j≤p-1,则(-1)i+jΔiz(n)>0,j≤i≤p-1;(b)若j≥1,则Δiz(n)>0,1≤i≤j-1。
2主要结果
定理1假设d为正整数且d≥1,b≤b(t)<1,(0≤b<1);若x(t)为方程(1)的最终有界正解,令y(t)=x(t)-b(t)x(t-τ),则最终成立
Δdy(t)≥0,Δd-1y(t)<0,Δd-2y(t)>0,…,Δy(t)<0,y(t)>0。
证明设x(t)为方程(1)的最终有界正解,则存在t1≥t0满足
x(t)>0,x(t-τ)>0,x(t-σ)>0,t≥t1≥t0。
设y(t)=x(t)-b(t)x(t-τ),由方程(1)及条件(H0)可得:
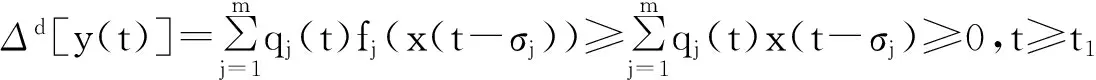
即
Δd-1y(t+τ)≥Δd-1y(t),t≥t1。
(2)
由条件可知Δdy(t)不恒为0,故Δd-1y(t)必最终为正或最终为负。进而推出Δd-2y(t),…,
Δy(t)都最终为正或最终为负。
假设Δd-1y(t)>0。则存在t2≥t1满足Δd-1y(t)>0。因此由(2)式可得
Δd-1y(t2+jτ)≥Δd-1y(t2),j≥1。
对上式将j从1到自然数m求和得
Δd-2y[t2+(m+1)τ]-Δd-2y(t2+τ)≥mΔd-1y(t2)。
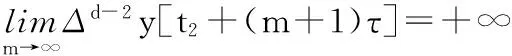
同理可得Δd-2y(t)>0,…,Δy(t)<0。由此可得y(t)>0最终成立。
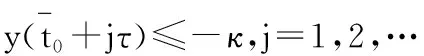
于是可得
对上式两边j从1到自然数m求和得
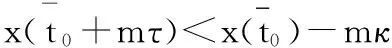
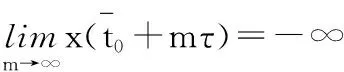
定理2方程(1)如果满足下列条件
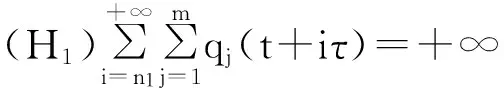
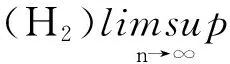
则方程(1)的有界解是振动的。
证明为了研究方程(1)的有界解的振动性,我们对d分情况进行讨论:

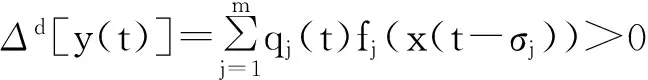
当0
所以有
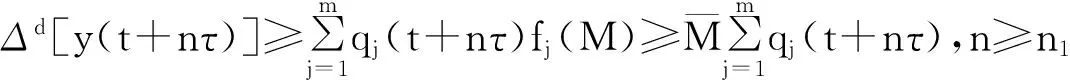
(3)
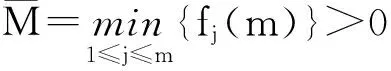
对(3)式两边的n从n1到n-1求和得
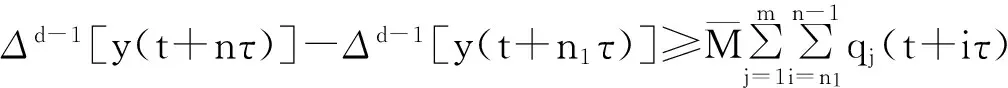
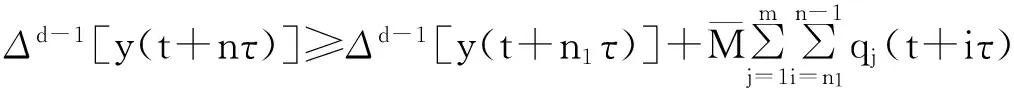
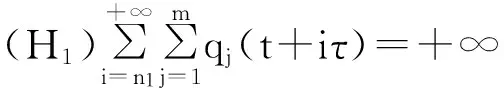

因y(t)=x(t)-b(t)x(t-τ),故y(t+τ)=x(t+τ)-b(t+τ)x(t)。
所以
y(t+τ)-y(t)
=x(t+τ)-b(t+τ)x(t)-x(t)+b(t)x(t-τ)
=x(t+τ)+b(t)x(t-τ)-(1+b(t+τ))x(t)。
又因{y(t+nτ)}有界且最终严格减少,所以y(t+τ) 从而得: x(t+τ)-x(t) 矛盾。 故当d为奇数且d≥1时,方程(1)的所有有界解振动。 (2)当d为偶数且d≥2时, 设x(t)为方程的有界正解,满足x(t)>0,x(t-τ)>0,x(t-σ)>0,t≥t1≥t0。 令y(t)=x(t)-b(t)x(t-τ),根据定理1可得,存在t2≥t1,使得 Δdy(t)≥0,Δd-1y(t)<0,…,Δy(t)<0,y(t)>0,t≥t2。 x(t)=y(t)+b(t)x(t-τ) ≥y(t)+bx(t-τ) =y(t)+b[y(t-τ)+b(t-τ)x(t-2τ)] ≥y(t)+by(t-τ)+b2y(t-2τ)+…+bh(t)-1y[t-(h(t)-1)τ]+bh(t)x(t-h(t)τ)。 (4) 由条件(H2)知存在充分小的ε(0<ε<1),使得 (5) 由于当t→∞时,h(t)→∞。且(0≤b<1)。所以对此ε存在t3≥t2+τ,使得 由(4)可得 (6) 对充分大的t4>t3,另t=t4+iτ,i是自然数。由(4)式和σ=kτ,有 由条件(H0)得 (7) 由于qj(t)∈([t0,+∞),+),j=1,2,…,m,且qj(t)为有界函数;x(t)为方程的有界正解。 所以存在q(t4+iτ)≤min{qj(t4+iτ)},x(t4+iτ-σ)≤min{xj(t4+iτ-σ)}。 由(7)式我们可得 Δd-1[y(t4+(i+1)τ)]-Δd-1[y(t4+iτ)]≥mq(t4+iτ)x(t4+iτ-σ)。 即 Δd-1[y(t4+(i+1)τ)]-Δd-1[y(t4+iτ)]≥mq(t4+iτ)x[t4+(i-k)]。 对上式从i 由定理1可得 对上式关于i从n-k到n求和可得 将上述过程做d-1次并根据定理1可得 y[t4+(n+1)τ]-y[t4+(n-k)τ]≤ 于是 y[t4+(n+1)τ]-y[t4+(n-k)τ]≤ y[t4+(n+1)τ]+y[t4+(n-k)τ] 与(7)式矛盾, 故当d为偶数且d≥2时,方程(1)的所有有界解振动。 综上所述方程(1)的有界解振动的。 参考文献: [1] LADAS G,PAKULA L,WANG Z.Necessary and sufficient conditions for the oscillation of difference equations[J].Panamer Math J,1992,2(1):17-26. [2] 张玉珠,燕居让.具有连续变量的差分方程振动性的判据[J].数学学报,1995,38(3):406-411. [3] 黄梅.具连续变量的变系数偶数阶差分方程的有界振动[J].应用泛函分析学报,2014,16(1):54-58. [4] 杨甲山,李继猛.具有连续变量的高阶非线性差分方程的振动与非振动准则[J].合肥工业大学学报(自然科学版),2010,33(6):934-938. [5] 赵良鹏,闫卫平.带有强迫项的高阶差分方程解的振动性[J].郑州大学学报(理学版),2014. [6] 唐清,干曾玲.高阶中立型差分方程的振动性及其非振动解的渐进性态[J].数学杂志,2000,20(2):207-210. [7] AGARWAL R P.Difference Equations and Inequalities[M]. New York: Marcel Dekker,1992. Bounded Oscillation for the Higher Order nonlinear difference Equation with continuous variable YANG Yuhui1,ZHAO Liangpeng2* (1.Department of Mathematics, Lvliang University, Lvliang,Shanxi 033000,China;2.School of Mathematics Science,Shanxi University, Taiyuan, Shanxi 030006, China) Abstract:Bounded Oscillation for the high-order nonlinear difference Equations was considered by using some analysis techniques.Some sufficient conditions for bounded oscillation of the solutions were obtained. Key words:difference equation ;bounded solution;oscillation;positive solution 文章编号:1004—5570(2016)02-0052-04 收稿日期:2015-07-16 作者简介:杨禹慧(1987-),女,助教,研究方向:微分差分方程及其应用,E-mail:yangyuhui20@126.com. *通讯作者:赵良鹏(1987-),男,硕士研究生,研究方向:差分方程理论及其应用,E-mail:zhaoliangpeng20@126.com. 中图分类号:O175.7 文献标识码:A