有限元反分析在隧道设计中的作用
2016-06-20邵根大编译
邵根大 编译
有限元反分析在隧道设计中的作用
在复杂的隧道施工的现代设计中,利用三维有限元分析(3D FEA)是最好的做法,其主要优点是能够了解实际施工过程的影响和十分重要的三维效果,三维效果是指在建隧道与相邻的既有结构之间的相互作用以及非均质地层的影响。
另一方面,二维有限元分析(2D FEA)可以作为简化模型进行计算,只要设计者认识到二维有限元模型的假定和局限性,计算表明,它可以用来校正、补充三维模型,甚至在某些情况下取代三维模型。
1 Farringdon地铁车站实例
下面以英国伦敦 Crossrail 的 Farringdon 地铁车站为例(图 1),讨论反分析在隧道施工设计中的作用。
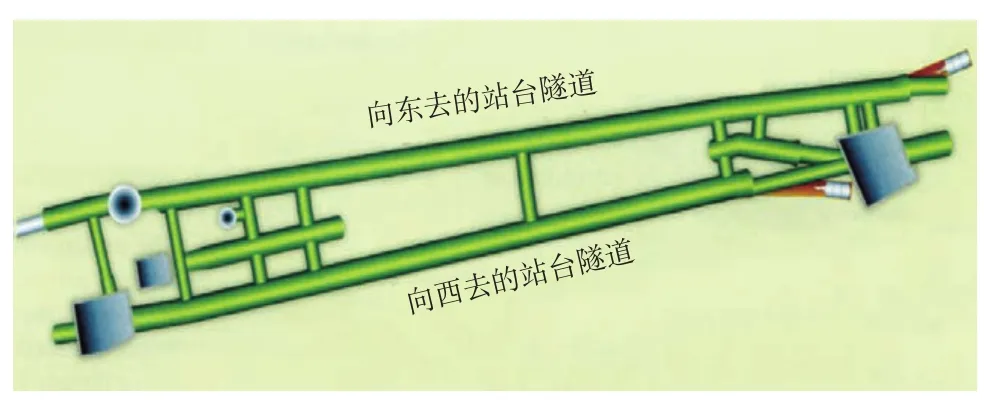
图1 Farringdon 地铁车站
这个车站是由 2 个设有站台的隧道组成。用盾构挖成的 2 个区间隧道,采用新奥法将其扩大为可设站台的车站隧道。原则上区间隧道的设计可以采用二维有限元分析,但是因为车站除站台隧道外,还包括售票厅、站厅隧道、竖井和横通道等结构,因此,有必要进行三维有限元分析。
设计的其他方面也需要考虑,诸如:几个重要参数的灵敏度评估分析;有效应力和孔隙水压力的耦合分析;固结分析;土壤本构模型;混凝土模型;开挖顺序(即新奥法施工的隧道工作面的分部开挖模拟)。然而由于时间和资源的限制,实际上这些问题不可能全部包括到三维有限元分析中。
2 有限元反分析模型
下面介绍采用三维和二维有限元分析的组合,对新奥法施工的隧道的实际性状进行反分析。在有限元模拟的计算中凸显反分析在隧道设计中的重要作用及其研究结论(图 2、图 3)。

图2 三维有限元反分析模型
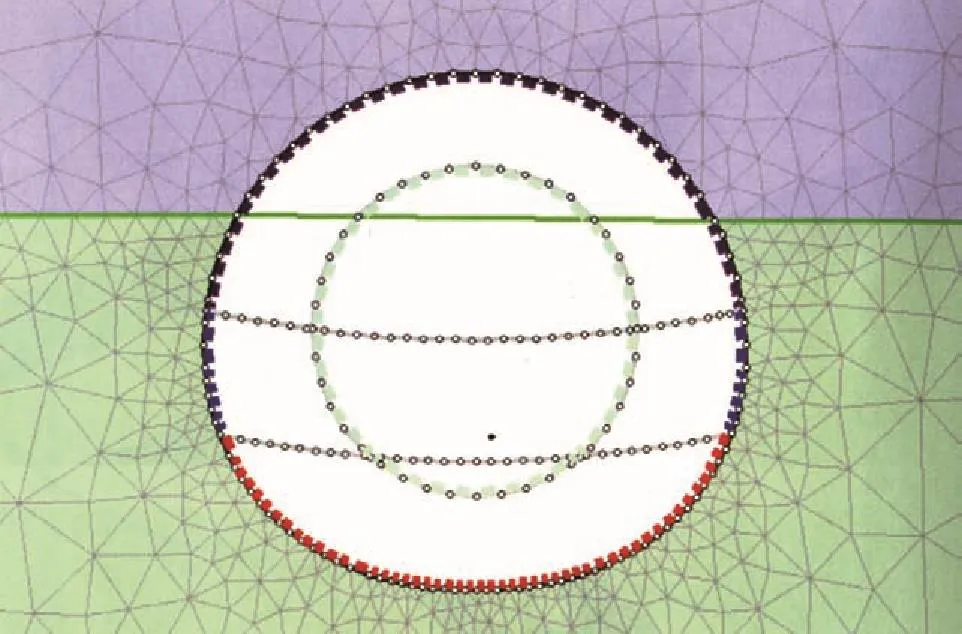
图3 二维有限元反分析模型
2.1反分析的作用
反分析通常应用于土木工程,广泛应用于边坡稳定问题。可以定义一种分析(有限元、极限平衡等),其参数和模型一直到结果出来之前都是可变的,参数和模型的变化导致答案的修正,这被称之为反分析。
一个应用反分析很好的实例是邓肯等有关边坡稳定的三维效应分析。边坡稳定问题在大多数情况下采用极限平衡分析或二维有限元分析,计算边坡稳定的安全系数。
然而,这种方法忽略了非常重要的三维效应,即边坡的长宽比几何特性和侧向剪力。在一般的分析中,由于忽略了这些因素,将会得出保守的安全系数。
然而,在反分析中,边坡垮塌了,其安全系数实际仅等于 1,问题在于未考虑三维效应,以致沿滑动面的土壤参数偏高,使计算成为非保守的结果。
类似的考虑对隧道设计来说也同样有效。为了获得隧道内和地表实际发生的变形,在隧道施工的反分析中,可以适当变化参数,有限元模型中的这些参数包括:土壤和混凝土的强度和刚度、模拟的施工步骤、有限元网格的几何形状。需要注意的是:参数的变化应在自然范围内;反分析的目的不是为了获得保守或非保守的答案,而是为了尽可能复制出计算对象的实际表现。
Farringdon 车站是 3 条线路的换乘站,施工期间向东、向西的 2 台盾构由此经过。该车站位于地下 30m,包括东、西 2 个售票厅,通过 2 部自动扶梯将站厅隧道、站台隧道连接起来。2 个站台隧道每隔 300m 设 1 个横通道和通风隧道。
2.2隧道内监测数据的采集
在 Farringdon 车站,对大约 1km 长的隧道采用高精度的全站仪进行变形量测,每隔 10m 设 1 个量测断面。典型的量测断面示于图 4 ,图 4 中 M1~M7 为测点 1~测点 7。随施工的进展每天采集测点的变形。隧道变形随时间的发展可分为 3 个阶段:初始变形阶段,连续 3~5天呈线性增长;渐趋稳定阶段,随着衬砌环的闭合隧道变形趋于稳定,持续 3~5 天;稳定阶段,附近不再有隧道开挖,读数有小的波动,但它与隧道变形无关。
在 Farringdon 车站内布置了密集的补偿注浆管网。为了排除补偿注浆的影响,在车站隧道量测范围内没有布置补偿注浆管。
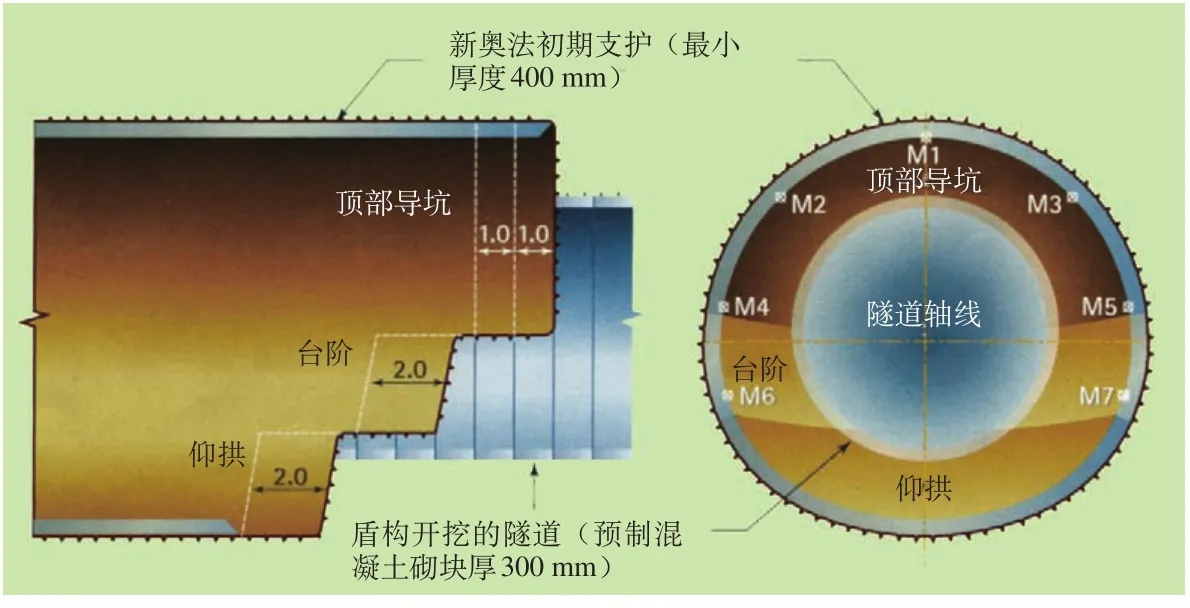
图4 车站隧道(高10.66 m,宽11.35 m)开挖、支护顺序,量测断面测点布置(单位:m)
2.3单独的三维有限元模型
出于对计算效率的考虑,把三维有限元模型分离出来,它们是西售票厅区模型、东售票厅区模型、出入井区模型以及联系西售票厅的3个连接通道模型。
这些单独的模型是为了解决特殊的设计问题,三维模型提供了考虑隧道施工中三维问题的机会,诸如地层与结构的相互作用问题,与工作面稳定掘进有关的地层损失与地层运动的信息,这些信息不带任何主观假定。
三维有限元设计分析的目的是确定复杂情况下的衬砌厚度(例如与其他隧道紧密相邻的 3 个连接通道),优化开挖程序,提供有实用意义的监控初始值。
ABAQUS,一个用于数值分析的有限元软件包。土壤材料用弹性—完全塑性摩尔—库仑模型模拟。由于初期支护不考虑防水,因此,在分析中采用不排水的土壤参数。为了考虑“快速施工”的影响,为此,与伦敦黏土的固结时间作了比较。
这种数值分析是在总应力分析的基础上进行的。黏土的不排水抗剪强度(Cu)和杨氏模量(Eu)随深度增加呈线性增长。
此外,Farringdon 的 2 个主要的地质特点——存在断层、伦敦黏土厚度变化,在模型中也进行了模拟。纤维加劲喷混凝土是作为线性弹性—完全塑性材料模拟的,考虑材料破坏后的性状,采用它的残余弯曲抗拉强度。
在所有模型中,对基于设计的开挖和支护顺序进行多步分析的模拟。1 个步长的开挖和支护分 2 步完成,第 1 步移走土壤,第 2 步安设支护。对大断面的车站和站厅隧道,根据设计模拟顶部导坑、台阶、仰拱的开挖顺序,断面小的横通道则根据设计模拟全断面开挖。

表1 隧道平均变形(不进行补偿注浆的区段)
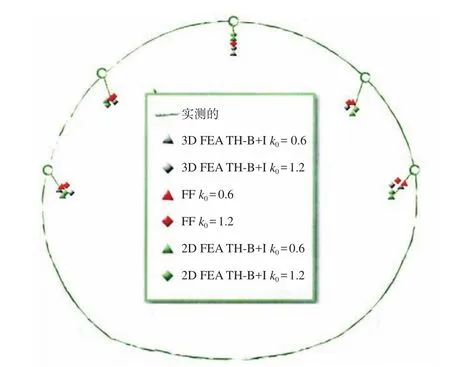
图5 隧道变形实测值与预测值的比较
2.4反分析优化
三维有限元反分析的主要目的是评估开挖类型的影响,也就是分部开挖(即顶部导坑、台阶和仰拱)和全断面开挖的影响。有以下不同的开挖类型:
(1)2 次顶部导坑、台阶、仰拱(TH-B-I);
(2)2 次顶部导坑、仰拱、台阶(TH-I-B);
(3)2 次顶部导坑,把台阶和仰拱合起来(TH-B+ I);
(4)全断面(F F),进尺 1m/1 环。
前3个类型顶部导坑步长 1m,开挖 2 次;台阶、仰拱步长 2m。
三维有限元分析的重要结论是,TH-B-I、TH-I-B、TH-B+I 模拟的差别很小,因此,可以用 TH-B+I 模拟替代。建立二维有限元模型,有助于多次反分析。
模拟的步骤如下:输入地质应力状态;把盾构开挖范围内的土壤按开挖顺序软化 50%;移走软化土壤,安设衬砌;模拟把盾构隧道扩大成车站站台隧道的分部开挖。
2.5有限元反分析结果与实测值的比较
反分析模型的校正考虑 3 个因素:尽可能准确预测隧道变形;尽可能准确预测地面沉降;避免低估衬砌应力。
为了比较隧道变形,将实测的隧道各测点的平均变形列于表 1。
图5 表示采用 2 个不同的土壤休止系数 k0的三维有限元、二维有限元反分析的结果,图 5 中:设计模型(FF k0= 0.6、k0= 1.2),三维有限元反分析模型(3D FEA TH-B+I k0= 0.6、k0= 1.2),二维有限元反分析模型(2D FEA TH-B+I k0=0.6、k0= 1.2)。
分析结果表明,三维有限元、二维有限元(k0= 1.2)拱顶的横向位移比实测的大,垂直位移比实测的小;三维有限元、二维有限元(k0= 0.6)计算的位移与实测的很好吻合。
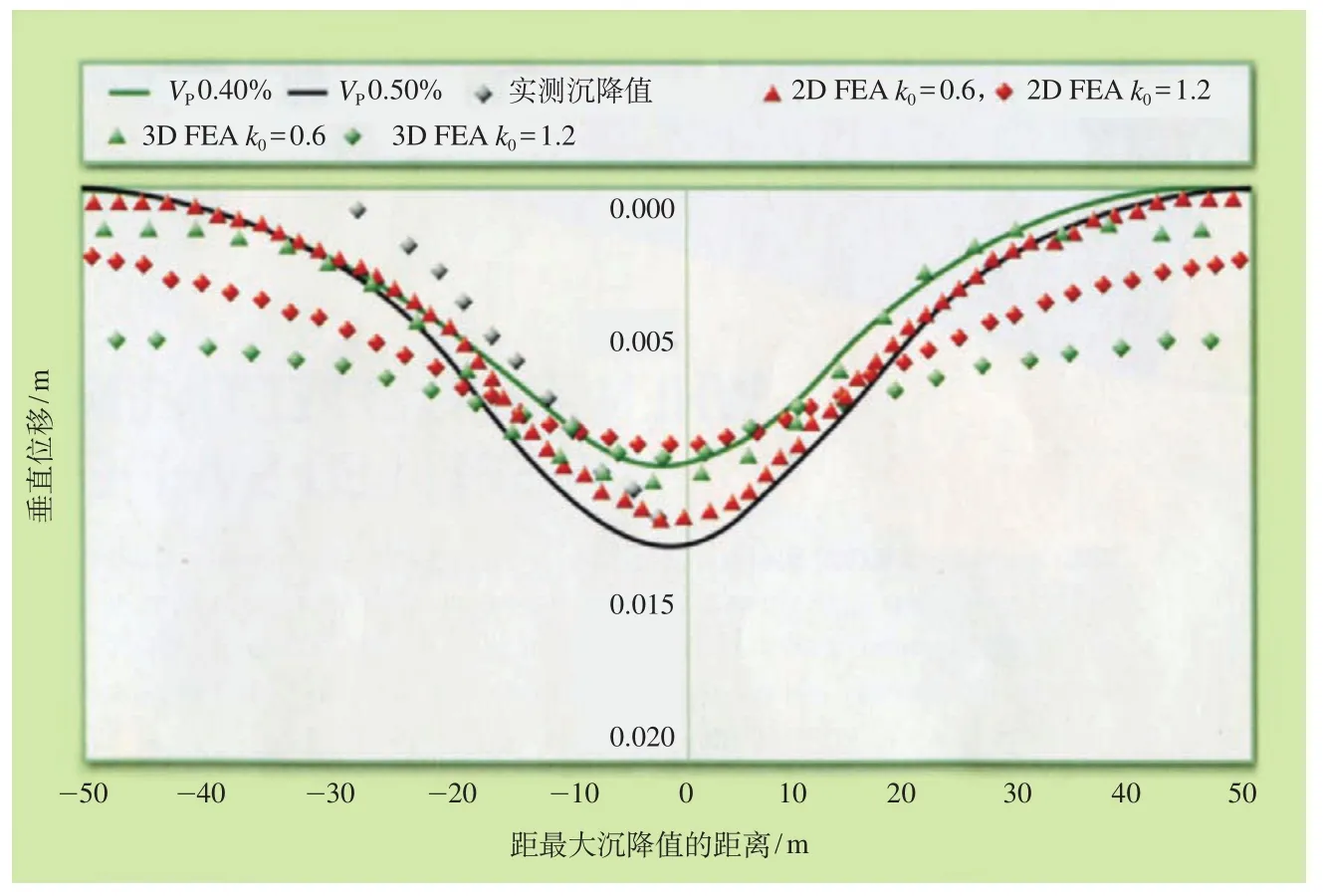
图6 实测的与预测的地面沉降槽的比较
为比较地面沉降,选择不进行补偿注浆的区段进行连续观测。采用 k0= 0.6、k0= 1.2 的模型在图 6 中进行比较,图 6 中还展示了采用不同地层损失量的地面沉降曲线。从图 6 可以看出,虽然地表土壤由于既有的建筑物基础的影响变得很硬,但三维有限元、二维有限元(k0= 0.6)分析得出了满意的地面沉降槽,其相应的地层损失量在 0.4%~0.5% 之间。这只是考虑了从盾构隧道扩大为车站站台隧道时的地层损失量,由盾构开挖引起的地层损失量未予考虑。
3 结论
(1)地面沉降预测中对土壤休止系数 k0值是非常敏感的。
(2)三维有限元分析中,把开挖步骤分成顶部导坑、台阶和仰拱,其分析结果与把台阶和仰拱合成一步完成的分析结果(隧道位移、支护应力)是相似的。
(3)三维有限元分析模拟全断面开挖(FF)与TH-B-I分部开挖产生非常相似的沉降槽,因此,简化成全断面开挖是可取的。
(4)对 Farringdon 车站的地层条件,采用 k0= 0.6 产生更实际的隧道变形和地面沉降。
(5)地层损失量只是考虑了车站隧道从盾构隧道扩大为车站站台隧道时的贡献,它在 0.4%~0.5% 之间变化。
(6)二维有限元分析得出的隧道变形和地面沉降非常可信。这是在两交叉口之间的车站隧道长度足以能产生与平面应变状态近似的计算条件,因而获得如此满意的结果。
参考文献
[1] Angelos Gakis,Stephen Flynn,Ali Nasekhian,et al. The role of inverse analysis in tunnel design[J]. Tunnels & Tunnelling International,2015(5):35-41.
邵根大 编译
责任编辑 冒一平
动态消息
伦敦黏土土壤特性:容重 20k N/m3;杨氏模量 40 + 3.7 zMPa;泊松比 0.495;不排水剪切强度85 + 6.5 zkPa;摩擦角 0°;土壤休止系数 k0为 1.2 或0.6;其中 z 为车站隧道深度。
收稿日期2015-12-14
