基于FLAC3D的加筋土填方边坡稳定性分析

段晓伟，耿少波

(1.长安大学 建筑工程学院，西安 710064；2.中北大学 土木工程系，太原 030051)



基于FLAC3D的加筋土填方边坡稳定性分析

段晓伟1，耿少波2

(1.长安大学 建筑工程学院，西安 710064；2.中北大学 土木工程系，太原 030051)

摘要：以陕西某山区高填方工程为背景，运用强度折减法和关联流动法则，对该场地某超高加筋土边坡夯后的水平位移、竖直位移、最大主应力、最小主应力等力学行为进行数值分析，研究了土工格栅对加筋高填方边坡稳定性的影响，并对土工格栅垂直间距参数设计进行比选和优化。结果表明：无筋边坡的潜在滑移面比加筋边坡更靠近坡面，加筋不仅能提高边坡安全系数，而且能降低边坡的最大剪应变与最大位移；筋材铺设存在最佳间距区域，合理的铺设间距能够有效提高加筋高边坡的稳定性。

关键词：加筋土；高填方地基；边坡稳定性；安全系数

0引言

随着城镇化进程的加快，建设用地日趋紧张，因此，越来越多的工程修建在山区。在自然错落的地形条件下，高填方、挖方边坡在工程中遇到的问题越来越棘手，由于地质条件复杂再加上一些不利的外部因素的影响，会使一些填方边坡在回填后出现较大变形，其稳定性往往得不到保证。因此山区填方边坡的变形和稳定性及其防治问题的研究引起了学者的高度重视[1-2]，有关边坡稳定性的研究也越来越多[3-4]。

加筋土技术是在土工合成材料的加筋作用下，增强边坡稳定性[5]，使填方边坡坡度增大，由此减小土方用量，节约工程占地，提高经济效益，目前被广泛应用于边坡、地基处理、公路路堤加固。对于加筋土边坡稳定性的分析是目前重要的研究课题之一。常采用的研究方法主要有：极限平衡法、极限分析法、滑移线场法、有限元法。这些建立在极限平衡理论基础上的各种稳定性分析方法一般假定土体为理想刚塑性体，滑裂面形状为折线、圆弧、对数螺旋线等[6]，沿滑裂面滑动，同时考虑加筋拉力增强了土体的稳定性，运用静力平衡的方法来分析与计算边坡的稳定性。但这些方法未全面考虑土体内部的应力应变，以及与筋材之间的相互作用等关系，也难以分析加筋土边坡发生破坏的过程；同时也没有考虑土体和支挡结构的相互作用，因而安全系数的准确程度很大一部分依赖于上述假定的合理性。而有限元法将加筋土的变形协调与应力应变关系结合起来，使得计算结果更加准确合理。FLAC3D有限差分法程序能较准确地模拟地质材料在到达强度极限或者屈服极限状态时所发生的破坏及塑性流动等力学行为，具有有限元法的优点，因此在边坡稳定性分析中被广泛运用[7-8]。

本文以陕西某山区高填方边坡工程为背景，运用加筋土挡墙的原理，采用FLAC3D程序中内置的强度折减法及流动关联法则求得加筋边坡的安全系数，并与未加筋的安全系数进行对比，建立5组不同的土工格栅垂直间距加筋土边坡模型，研究加筋土间距对边坡稳定性的影响。

1加筋土挡墙原理

经过多年来加筋土试验和加筋工程的研究，学者们提出了多种加筋机理：有摩擦加筋原理、准粘聚力原理、张力膜理论、加筋垫层的应力扩散作用理论等。其中摩擦加筋原理和准粘聚力原理得到较普遍的认同。

(1)摩擦加筋原理。土体与筋材界面之间存在摩阻力和咬合力，筋材约束了土体的侧向位移，增加了土体的刚度，进而提高了加筋土体的强度和稳定性[7]。

(2)准粘聚力原理。加筋土结构可以视为各向异性的复合材料[9-10]，拉筋与土体之间共同作用产生抗剪力、摩阻力、抗拉力，使加筋土结构稳定性大大提高。

2工程实例分析

2.1工程概况

拟建场地西区地形起伏较大，南北向长约1.4 km，东西向宽约0.7 km。均采用开挖回填方式形成场地，原始地貌为典型的V字形沟谷地形，西区的填方采用分层回填加分层强夯后，冲沟沟口形成52 m的超高填方边坡，边坡结构采用土工格栅加筋边坡，0～30 m坡度为1∶1，31～52 m坡度为1∶0.75。西区高填方现场回填与强夯示意图见图1。根据勘察资料，边坡力学参数见表1，土工格栅的物理力学指标见表2。

图1　高填方现场回填与强夯示意图

坡高/m宽高比泊松比弹性模量/MPa重度/(kN·m-3)粘聚力/kPa摩擦角/°521∶1.50.320203528

表2　土工格栅的物理力学指标

2.2基本原理

采用FLAC3D内置的强度折减法计算安全系数。强度折减技术在有限差分法中可以表述为：土体重力加速度恒为常数，逐步减小抗剪强度物理量，即将c，φ值同时除以折减系数FS，得到新的强度指标c′，φ′，通过有限差分法计算分析，反复试算至临界破坏状态，这样强度折减法的安全系数为：岩土体的实际抗剪强度与临界破坏状态时折减后的剪切强度比值[11-12]，即为此时采用的强度指标与岩土体原具有的强度指标之比。公式如下：

c′=c/FS，

(1)

(2)

式中c′为折减后的粘结力，φ′为折减后的摩擦角，FS为折减系数。

2.3计算模型的建立

计算模型采用FLAC3D中的Mohr-Coulomb非线性本构模型及相关联流动法则，初始应力场按自重应力场考虑，不考虑地下水及地震的影响，边界条件为下部固定约束，左右两边法向约束，上部为自由边界，忽略轴向变形，模型的计算简化为平面应变问题，以数值分析计算的收敛性作为失稳的判断依据。筋带及网格划分示意图如图2所示。

图2　筋带及网格划分示意图

2.4计算结果对比分析

2.4.1安全系数

为了研究加筋边坡的稳定性及筋材的铺设间距对加筋效果的影响，计算了不加筋边坡以及加筋边坡时5组不同土工格栅间距下的安全系数，统计表见表3，安全系数随间距的变化曲线见图3。

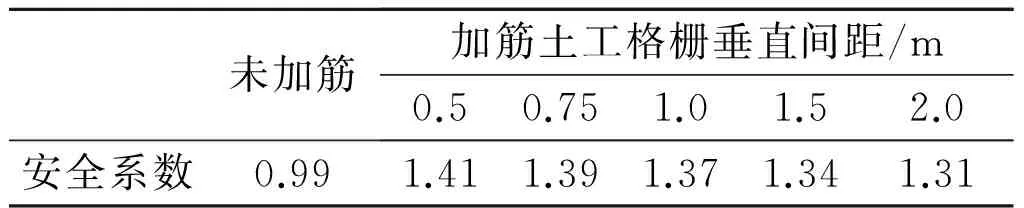
表3　边坡安全系数随格栅垂直间距的变化

由表3可知，当填方体填筑完成后，边坡不处理的安全系数为0.99(小于1.3)，不能满足一级边坡稳定性的要求；采用加筋技术处理高填方边坡，安全系数都大于1.3，稳定性能够满足要求，说明边坡加筋后，抗剪强度增加，稳定性大大提高。

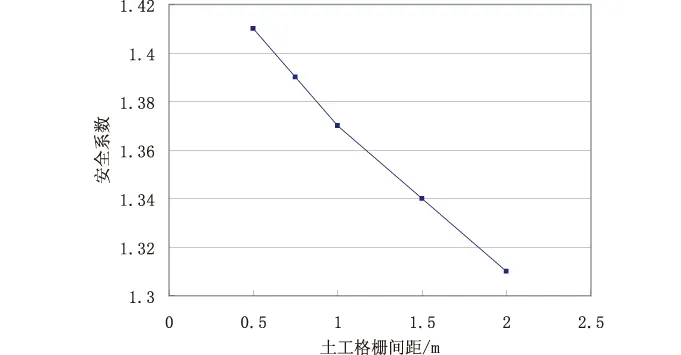
图3　安全系数随土工格栅间距的变化曲线

随着土工格栅的铺设间距增大，安全系数在减小。土工格栅间距为2 m时，安全系数为1.31，仍然大于1.3，远远大于不加筋时的0.99；间距为0.5 m时，安全系数达到1.41，安全性能大大提高，稳定性也满足要求。这也充分说明加筋处理此边坡是成功的，也说明在筋材的铺设施工过程中，筋材间距是关键，它对加筋土边坡的稳定性影响很大，合理的铺设间距不仅能够提高其稳定性，而且能够提高经济效益。实际施工过程中，筋材间距太小，影响工程进度和工期，土工材料也有剩余，造成浪费；间距太大，加筋作用不显著，不能确保安全。因此必须优化施工方案，找到一个最佳间距区域，发挥最大的加筋作用，使工程成本降低，同时也最大化地实现工程效应。2.4.2剪应变及最危险滑移面

图4为用FLAC3D内置的强度折减法计算出的不同土工格栅铺设间距下的边坡平面剪应变分布情况。

由图4可见，边坡不处理时，边坡的剪应变增量最大值为9.057×103，主要集中出现在边坡脚部，形成了贯通的剪切滑移面，表明破坏区域与剪切滑移面构成的破裂面贯通，边坡整体不稳定。经过加筋处理后的边坡剪应变增量最大值均小于不处理的情况，滑移面中部均未出现剪应变增量集中的情况；未做处理的边坡潜在滑移面比加筋边坡更靠近坡面。可见加筋土后效果显著，大大减小了剪应力较高的点，其区域也相应地减少，原因是加筋土结构通过界面的应力传递，改变了土体的应力应变关系，筋带给土体提供了侧限，从而使边坡的应力场、位移场重新分布。筋带不仅分担了一部分单独土体时应承担的剪力，使土体所受的剪力减小，而且剪切面上的正应力有所增加，土体的抗剪强度进一步增强，因而其稳定性也相应提高[5]。

2.4.3最大水平及竖向位移

表4为用强度折减法计算出的不同土工格栅间距下的边坡最大水平位移及竖向位移。由表4可见，加筋处理后均能够有效地减小边坡的最大水平位移及竖向位移，合理的土工格栅间距能够最大程度地阻止边坡体向外移动及边坡体的沉降。

(1)未加筋　　　　(2)间距为2 m

(3)间距为1.5 m　　　　(4)间距为1 m

(5)间距为0.75 m　　　　(6)间距为0.5 m图4　剪切应变增量等值线图

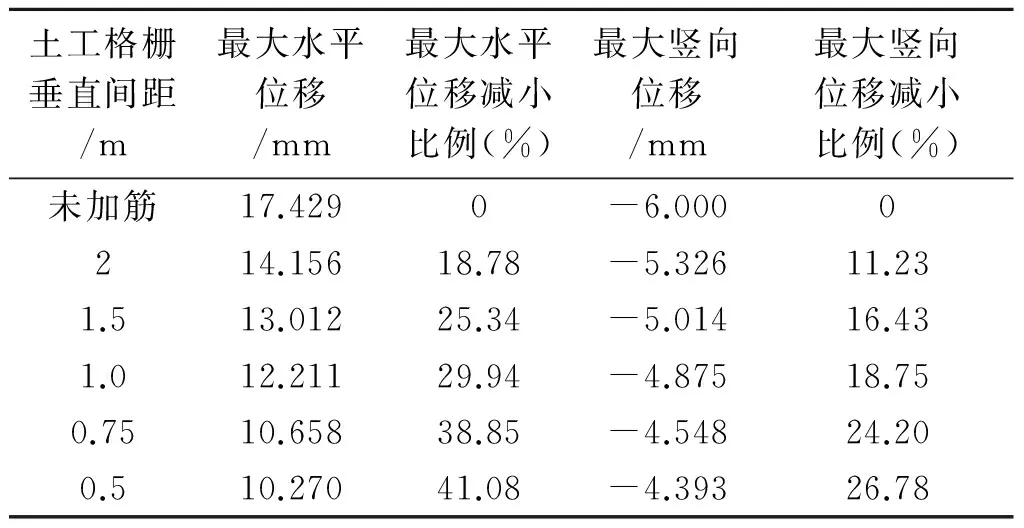
土工格栅垂直间距/m最大水平位移/mm最大水平位移减小比例(%)最大竖向位移/mm最大竖向位移减小比例(%)未加筋17.4290-6.0000214.15618.78-5.32611.231.513.01225.34-5.01416.431.012.21129.94-4.87518.750.7510.65838.85-4.54824.200.510.27041.08-4.39326.78

坡脚的水平位移与土工格栅垂直间距关系见图5。由图可知，坡脚点水平位移随土工格栅的垂直间距的增加而逐渐增大，增加速率幅值逐渐变大。垂直间距为0.5 m时，坡脚水平位移为10.158 mm；间距变为0.75 m时，坡脚水平位移为10.270 mm，增加0.112 mm，变化微小；当间距为1.0 m时，坡脚水平位移为12.211 mm，增加1.941 mm，增加速率幅值增大，可见土工格栅间距的选择至关重要。

图5　坡脚水平位移与土工格栅垂直间距的关系

2.4.4最大主应力及最小主应力

限于篇幅，仅以52 m高土工格栅垂直间距1.0 m加筋土边坡与未加筋的边坡进行对比分析。最大主应力云图如图6所示，最小主应力云图如图7所示。

(1)未加筋

(2)间距为1.0 m图6　最大主应力云图

由图6可知，边坡未做处理时，边坡压应力最大值为845.91 kPa，坡顶未出现拉应力，在坡顶所在的填筑面上出现很小的拉应力，最大值为7.63 kPa。加筋后边坡的应力集中现象不明显，表现为越靠边坡底部，压应力越大，坡面基本与最大主应力云图平行，边坡压应力最大值为841.15 kPa。只在坡顶很小区域处出现的拉应力，最大值为16.01 kPa。说明加筋后拉结作用明显。

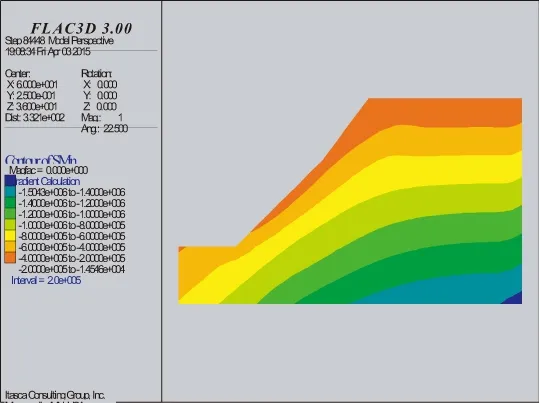
(1)未加筋

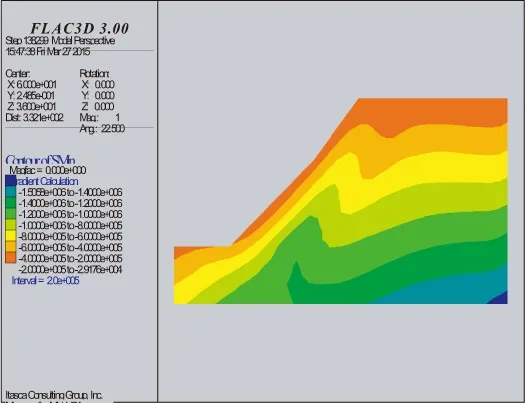
(2)间距为1.0 m图7　最小主应力云图

由图7可知，边坡的应力集中现象均不明显，两边坡的最小主应力均在坡脚处出现轻微的突变，影响不明显。

3结论

通过剪切应变增量等值云图、水平位移等值云图、垂直位移等值云图、最大主应力云图、最小主应力云图进行对比分析，得到以下结论：

(1)在山区场地高填方稳定性分析中，应用FLAC3D内置的强度折减法和相关流动法则具有一定的可行性和准确性。

(2)加筋处理后边坡的安全系数有所提高，滑移面中部均未出现剪切应变增量集中现象。无筋边坡的潜在滑移面比加筋边坡更靠近坡面，并很大程度地减小边坡的剪应变和最大位移。这充分说明加筋土挡墙是高填方地基人工边坡处理的一种有效方法。

(3)合理的铺设间距对于加筋土边坡稳定性至关重要，限于篇幅，本文仅列了5组间距，存在一定的局限性，筋材铺设必然存在一个最佳间距区域，需要进一步分析研究。

参考文献：

[1]王衍汇，倪万魁，石博溢，等.延安新区黄土高填方边坡稳定性分析[J].水利与建筑工程学报，2014，12(5)：52-56.[2]介玉新，秦晓艳，金鑫，等.加筋高边坡的稳定分析[J].岩土工程学报，2012，34(4)：660-666.

[3]建鑫龙，梁倩，张殿风.基于MARC土工格栅加筋挡土墙的有限元分析[J].路基工程，2015(4)：168-171.

[4]刘新喜，戴毅，陈向阳，等.炭质页岩软弱夹层路堑边坡稳定性分析[J].湖南文理学院学报，2015，27(4)：69-74.[5]陈金锋，宋二祥，徐明.强度折减有限元法在昆明新机场高填方边坡稳定分析中的应用[J].岩石力学，2011，32(增)：2585-2592.

[6]郑颖人，赵尚毅.岩土工程极限分析有限元法及其应用[J].土木工程学报，2005，38(1)：91-98.

[7]孙书伟，林杭，任连伟.FLAC3D在岩土工程中的应用[M].北京：中国水利水电出版社，2011.

[8]耿敏，赵文忠，王丙兴，等.基于FLAC3D的加筋土计算方法对比研究[J].河北工业大学学报，2013，42(3)：74-78.

[9]《土工合成材料工程应用手册》编委会.土工合成材料工程应用手册[M].2版.北京：中国建筑工业出版社，2000：218-232.

[10]Andrzej Sawicki.Plastic limit behavior of reinforced earth[J].Journal of Geothchnical Engineering，1983(109)：1000-1005.

[11]赵尚毅，郑颖人，时为民.用有限元强度折减法求边坡稳定安全系数[J].岩土工程学报，2002，24(3)：343-346.[12]吴世佳.边坡稳定性分析的极限平衡法FLAC3D模拟方法的对比研究[D].太原：太原理工大学，2011.

(责任编校：夏玉玲)

An FLAC3D-Based Analysis of the Stability of Reinforced-Earth-Filled Slopes

DUAN Xiao-wei1， GENG Shao-bo2

(1.School of Architecture Engineering，Chang’an University， Xi’an 710064， China；2.Department of Civil Engineering，North University of China， Taiyuan 030051， China)

Abstract：With the high filling project of a certain mountainous area in Shaanxi Province as the research subject， the authors of this paper have conducted a numerical analysis of the horizontal displacement， vertical displacement and maximum principal of the highly-reinforced-earth-filled slopes with the strength reduction method and the associated flow rules， studied the influence of geogrids on the stability of slopes filled with reinforced earth， and compared and optimized the designs of vertical spacing parameters of geogrids. The results show that the potential slip surface of non-reinforced slope is closer to the slope surface， that reinforcement can not only increase the slope safety， but also reduce the maximum shear strain and maximum displacement of slopes， that there exists an optimal spacing region for laying reinforcing material， and that the reasonable laying spacing can effectively improve the stability of reinforced slopes.

Key Words：reinforced earth； high-filling base； slope stability；coefficient of safety

基金项目：国家自然科学基金资助项目(51408558)

作者简介：段晓伟(1994-)，男，山西太原人，本科生，主要从事土木工程研究。

中图分类号：TU441+.5

文献标志码：A

文章编号：1672-349X(2016)03-0075-05

DOI：10.16160/j.cnki.tsxyxb.2016.03.021