融通，让学生学有结构的数学——“分数的意义”教学片段与反思

◇金一民

融通，让学生学有结构的数学
——“分数的意义”教学片段与反思

◇金一民

片段一：纵向融通，认识单位“1”

1.理解“1”。

（从左到右依次出示图1）

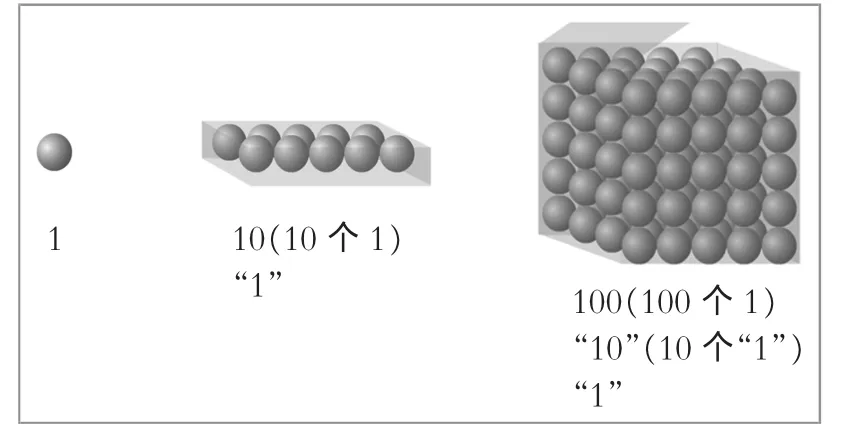
图1

师：1个乒乓球可以用1表示。10个乒乓球可以用哪个数表示？

生：可以用10表示。

师：对，这个问题一年级的小朋友都知道。问一个五年级水平的问题，10个乒乓球还可以用哪个数表示？

生：可以用“1”表示，把10个乒乓球看成一个整体。

师：那100个乒乓球可以用哪个数表示？

生：可以用100表示。

生：还可以用“10”表示，把刚才的10个乒乓球看作“1”，那就有10个“1”。

生：还可以用“1”表示，把100个乒乓球看作一个整体。

师：我们可以把1个乒乓球看作“1”，也可以把10个乒乓球甚至100个乒乓球看作“1”，还可以把什么看作“1”呢？

……

师：看来这个“1”无所不包，无所不能，这个“1”和我们一年级学的1有什么不同呢？

（不仅可以表示一个物体，还可以表示由许多物体组成的整体）

2.理解单位“1”。

师：如果把1个乒乓球看作“1”，那这些乒乓球必须看作几？

生：看作10和100。

师：这个10和100是怎么来的？

生：10个1，100个1。

师：如果把这些（10个）乒乓球看作“1”，那这些（100个）乒乓球必须看作几？

生：必须看作“10”。

师：这个“10”又是怎么来的？

生：10个“1”。

师：这些都是整数，现在你知道整数是怎么来的吗？

生：1个1个地数，就能数出2、3、4……100甚至更多。

师：这里的“1”可以表示1个，也可以表示10个、100个等。我们可以一个一个地数，也可以十个、一百个、一千个地数，这里的“1”就是一个单位，所以我们可以在“1”前面加上“单位”，数学上叫单位“1”。

反思：本课中，我基于学生对分数的初步认识和对整数、小数的认识展开教学，实现纵向融通。我把这一环节分成了理解“1”和“单位‘1’”两个层次。在理解“1”这个环节里，我借助“乒乓球计数”这一具体情境，激活学生对于分数初步认识中“一个物体”和“一个整体”的经验，通过比较理解“1”的意义：既可以表示一个物体，又可以表示由一些物体组成的整体。事实上，“数”具有相对性：把1个乒乓球看作 “1”，10个、100个乒乓球可以用10、100表示，如果把10个乒乓球看作“1”，100个乒乓球就应该用“10”表示……这就让学生理解了“1”作为一个单位的含义，对之后抽象数的本质具有重要意义。

片段二：横向融通，理解“数”的本质

1.理解“整数是数出来的”。

（出示图1）

师：这10个乒乓球的10是怎么来的？100呢？

生：是由10个1、100个1组成的。

生：是一个一个数出来的。

师：这些都是整数，想一想，整数是怎么来的？

生：整数都是用1数出来的。

2.分数是分出来的。

师：把10个乒乓球看作单位“1”，1个乒乓球看作几？为什么？

师：如果把这100个乒乓球看作“1”，那这10个乒乓球看作几？1个乒乓球呢？为什么？

生：10个乒乓球就是把 100个乒乓球看作“1”，平均分成10份，表示这样的1份，就是个乒乓球就是把100个乒乓球平均分成100份，每份就是它的

师：整数是用1数出来的，那分数又是怎么来的？分数能一个一个地数出来吗？为什么？

生：分数不满1个单位，是把“1”平均分得到的。

3.理解“分数也可以数出来”。

（概括分数意义后，教师出示图2）

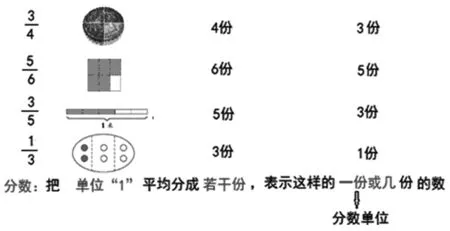
图2

师：分数是从单位“1”平均分得到的，能不能也像整数一样数出来呢？这个能不能数出来呢？拿什么来数？

（生答略）

4.整数、分数、小数都可以数出来。

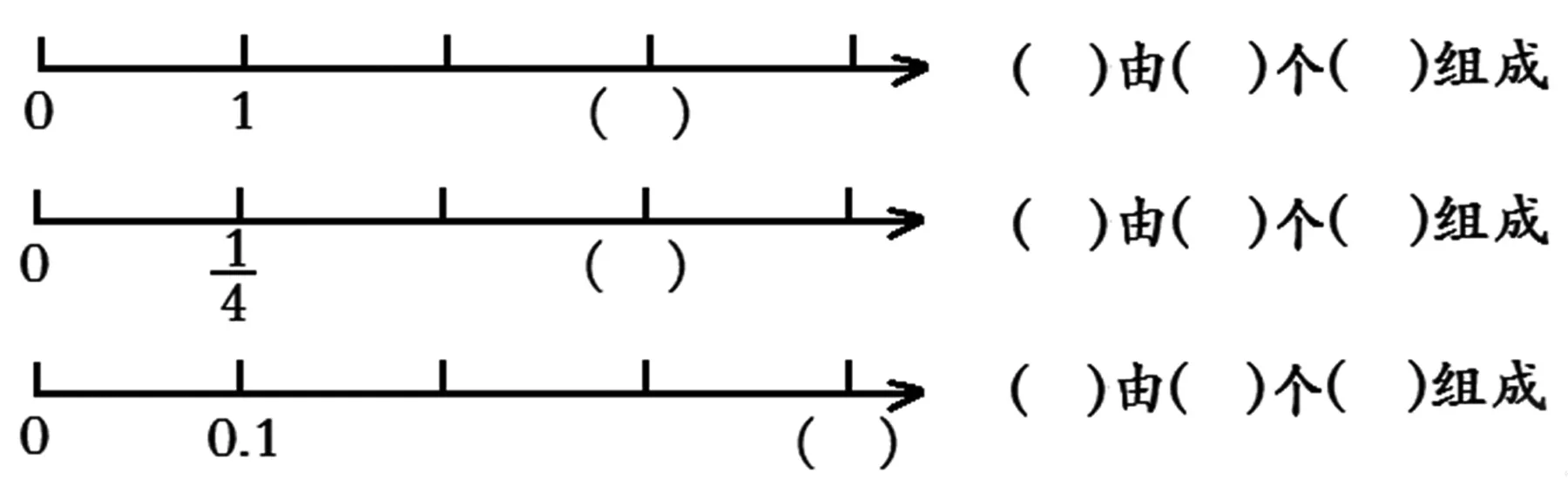
图3

（交流答案后）

师：你发现整数、分数和小数的组成有什么共同点？和同桌交流。

生：都是由计数单位累积而成，都有自己的计数单位。

师：大家看，整数、分数都与“1”有关，这是它们的相同之处；但整数是数出来的，分数是分出来的，这是它们的不同之处；最后我们发现，其实整数、分数、小数都可以数出来，这就是“大同”。数学，就是这么简单而深刻！

反思：事实上，整数、分数、小数的计数本质是“数源于数”，即数都是用它自己的计数单位数出来的，这是构成“数”结构的“大观点”。

本课中，我引导学生结合具体情境理解“整数是用‘1’数出来的”“分数是由‘1’分出来的”，再进一步理解“分数也可以数出来，是用自己的分数单位数出来的”，最后归结到“整数、分数、小数都可以数出来”，让学生体验“相同—不同—大同”的过程。

（作者单位：江苏常熟市实验小学）