站在运动的视角看图形,感受数学的神奇与美丽
——以“运动的圆”为例
2016-06-19刘克臣
◇刘克臣
站在运动的视角看图形,感受数学的神奇与美丽
——以“运动的圆”为例
◇刘克臣

谈话引发的调研
上四年级的儿子放学归来,他刚刚学完四边形的认识。我随意问:“四根小棒,分别长10厘米、10厘米、8厘米、8厘米,可以围成几个不同形状的四边形?”
儿子脱口而出:“1个长方形!哦,不对!2个,还有平行四边形!”
“到底几个? ”我追问。
“肯定是3个,还有一般四边形!”
我以为他没有理解我的意思便说道:“你画下来吧。 ”
画的结果和他说的一样,之后我也画了一个和他不一样的平行四边形,还没等我说话,他就说道:“这不也是平行四边形吗?都一样!”
“形状一样吗? ”
“一样!都是平行四边形,对边平行且相等的四边形! ”
对话被迫中断,我也冷静了下来。为什么明明形状不一样的两个图形他却坚信一样呢?其他孩子也有类似认识吗?
带着思考,我进行了类似的调研。这次我有备而来,事先准备了一个平行四边形框架。与3个学生谈话的过程和与儿子的谈话如出一辙,尽管我用框架演示推拉,他们依然坚信:形状一样,都是平行四边形!
为什么?首先看教材,小学阶段对图形的认识主要停留于边、角的特点,虽然新课程改革后教材安排了图形与运动的内容,但是这些运动都是基于全等变换,对于图形自身的变化缺乏必要的研究和关注。
再看实施过程,我们强调了图形的分类,即抽取概念的本质特征,却忽略了个性特征,自然会影响到学生的认识,从而使他们有按名称归类的想法,并认为所有平行四边形都一样。
为了进一步弄清原因,我选择圆来进一步调研:“说一说,你眼中的圆是什么样子的?”
“圆是曲线图形。”
“圆有半径和直径,半径是直径的一半。”
“圆有无数条对称轴。”
“圆,一中同长。 ”
学生的回答准确且充满理性。但是,如果我们把眼光从教室移向窗外,可以发现生活中许多圆都是以运动的状态存在的。而这种最直接的认识和体验已经随着对圆的学习“不断深入”反而淡化了。
如何引起学生对于图形运动特点的关注?圆运动起来小学生可以研究什么呢?
一则广告带来的“意外惊喜”
一天晚上,电视直播篮球比赛,其间插播了一个矿泉水的广告。我被这个广告搞得稀里糊涂,不知其意,后来查阅资料方知,广告讲述的是笛卡儿动人的爱情故事。
52岁的笛卡儿邂逅了18岁的瑞典公主克里斯汀,并当上了她的数学老师。公主的数学成绩在笛卡儿的悉心指导下突飞猛进,他们每天形影不离,彼此产生了爱慕之心。
没过多久,他们的恋情传到了国王的耳朵里。国王大怒,下令马上将笛卡儿处死。在克里斯汀的苦苦哀求下,国王将他驱逐出国,公主被软禁。
拿到信的克里斯汀找来纸和笔,把方程用图形画了出来。一颗心形图案出现在眼前,克里斯汀禁不住流下感动的泪水。这条曲线就是著名的“心形曲线”。
感动之余,进一步了解笛卡儿心形曲线。这条曲线实际上是两个大小相同的圆,在其中一个圆上选择一点,然后围绕另一个圆滚动一周后产生的,如图1:
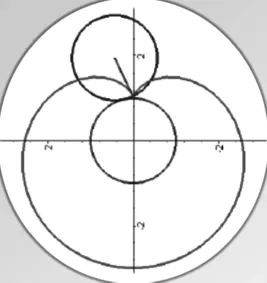
图1
圆的运动多么神奇和美丽,灵感油然而生:运动可以产生轨迹,何不从轨迹的角度入手呢?
从运动轨迹角度认识圆是否可行
有时候想法是美好的,但实施起来还要考虑学生的年龄特点和知识基础。轨迹对于学生来讲是一个陌生的概念,学生能理解吗?圆中最特殊的一个点就是圆心,圆心在运动过程中的轨迹是什么样呢?还是先进行一个小范围的学生调研吧:(1)如果用笔尖插在圆形纸片的圆心,然后圆水平滚动,笔尖画出的轨迹是什么样的图形?如果绕着一个圆滚动呢?(2)如果绕着一个正方形滚动呢?
第一个问题,学生都能很快回答出是直线和圆形。对于第二个问题,10个学生中有8人很快做出了错误回答:正方形!还有2人刚开始说是正方形,但有些犹豫,没有给出最后答案。大家提出画一画,最后经过动手实践给出了基本正确的答案。
这是一个非常有意义的调研!首先,打消了我的疑虑,这个内容的学习在小学阶段是可行的,学生对轨迹的理解并没有困难和歧义;其次,暴露了学生存在的错误认识,即认为沿什么运动,轨迹就是什么形状的;再次,发现了学生的学习路径,即动手实践。
我的设计
结合学生的认知特点,经过反复推敲与实践,本节课主要设计了以下活动:
生1:詹天佑你是总工程师,应该只需在家搞搞设计,遥控指挥就行了,为什么要亲临场地呢?真是与民同苦,率先垂范呀!
1.借助生活现象认识运动轨迹(如图2)。

图2
该环节中,车轮轨迹贴近学生生活,金星和地球运动轨迹虽然看不见但客观存在。第三幅图先让学生想象轨迹的由来,学生展开想象之后,教师揭示这是一种特殊的浇灌喷头浇灌过程中的轨迹。
2.研究圆沿直线和圆形运动时圆心的轨迹。
该环节的目的是让学生利用“一中同长”来解释轨迹,突出圆的特征。
3.猜想、验证圆沿正方形外围滚动一周后圆心的轨迹(如图3)。
图3
该环节主要让学生经历猜想验证的过程,突出动手实践的意义和价值。
4.玩万花尺(如图4),感受数学好玩。

图4
该环节主要让学生通过玩万花尺感受运动的神奇和美丽。
5.拓展延伸,感受运动的神奇与美丽。
实践后的反思
这节课我在不同地区进行了实践,每一次都能引发学生浓厚的学习兴趣,引发老师们的热议。
1.实践中深入理解“一中同长”。
教学中,老师们都会引用“一中同长”来揭示圆的本质特征,但在实际教学中,学生对此的理解往往停留在一个中心,所有的半径长度都相等。如何促进学生对“一中同长”意义的理解?我有针对性地设计了以下活动。
活动1:让学生解释为什么圆沿直线运动圆心轨迹是一条直线,沿圆运动是一个圆形。对于这两个问题,由于学生有生活中车轮的经验,都能认识到在运动过程中圆心距地面的距离保持不变。
活动2:圆沿正方形外围运动圆心轨迹是圆角矩形(如图5)。由于经验的影响很多学生开始都会认为,沿正方形外围滚动圆心轨迹是个正方形。经过动手实验之后,发现当滚动到4个顶点的时候轨迹变成了曲线。为什么是曲线呢?学生解释时需要用到“一中同长”的特点。

图5
活动3:玩万花尺,画出圆。利用万花尺怎样就能画出圆呢?学生不难想到选择圆心那个小孔。为什么?有了前面的学习经验,学生都能利用“一中同长”的特点进行解释。
2.挑战中激发问题意识。
每个人内心都有挑战自我的欲望,在这节课中,我设计了具有挑战性的问题。如在解决了圆沿正方形滚动的问题后,我话锋一转,提出“圆绕正方形滚动,圆心的轨迹真的不能是正方形吗”这一极具挑战性的问题,因为学生刚刚验证过不是正方形。
如何启发学生变换角度思考问题呢?我启发学生把圆放到正方形里面,想象圆心轨迹是什么,并动手实验。
更有意义的是,这样的挑战性问题能激发学生的问题意识,如学生提出:如果沿等边三角形旋转,圆心轨迹是什么样?再如,圆沿一个图形内侧滚动,圆心轨迹就是什么样呢?……
3.运动中感受数学的神奇和美丽。
玩万花尺是最为放松和高兴的环节,在不断尝试中,学生从开始玩得有些笨拙、毫无目的,到发现可以画出神奇的图案,被自己笔下美丽的作品所折服,不断发出惊叹。下面(如图6)是上课过程中学生的作品:

图6
运动的神奇和美丽还体现在数学文化和自然现象中。课尾,我向学生介绍了笛卡儿的心形曲线故事,并回顾课堂引入关于金星和地球的运动轨迹,演示了地球和金星8年的相对位置运动图,如图7所示:

图7
课堂中的每一个人都被震撼了!
从静到动看图形,学生看到了变化,看到了运动的神奇和美丽,看到了不一样的数学!我看到了惊喜,看到了认识图形教学的新视角!我相信,图形运动,神奇一定会延续……
(作者单位:北京市西城区教育研修学院)
