质疑、猜想、验证
2016-06-18龚宙
龚宙
【摘 要】在新课程的课堂上,动手实践、自主探究与合作交流是学习数学的有效方法。教师应当充分调动学生学习的积极主动性,关注思维发展,激发学习兴趣,鼓励学生学会质疑、合理猜想、积极验证,在探究活动中不断提升数学素养。
【关键词】质疑;猜想;验证;探索
中图分类号:G623.5 文献标识码:A 文章编号:1671-0568(2016)15-0060-02
一、教学案例
学习了几分之一后,在讨论把一个长方形平均分成四份的方法时,课堂中出现了插曲。除了常见的几种分法外,有一位同学提出了不同的想法。
生1:还可以斜着(沿着长方形的两条对角线)分,每一份也是长方形的四分之一。
师板书。(见图1)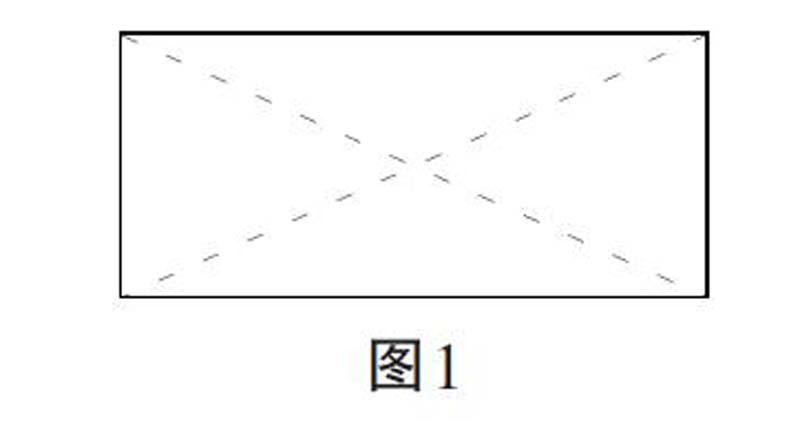
师:都同意吗?
生2:我认为这样分不是平均分,因为每份不一样。
师:其他同学的意见呢?
生3:这种分法,分成的4份形状不一样,我也觉得不是平均分。
大部分学生认同这种想法。
生1(坚持):我觉得是的,感觉是的。
少数同学同意,教室里开始出现争论。
师:有的同学直觉上认为这是一种平均分,也有同学认为分成的4份形状不同,那么大小也不同,不是平均分。到底哪种想法有道理,不能只靠直觉去判断,还是得动脑筋去——
生(齐声):验证。
师:你们打算怎么验证?
生1:老师,您告诉我三角形的面积公式,我量了以后求面积,看看是不是相等。
师:三角形的底、高、面积,我们都还没有学习,你已经知道了面积这个数学名词,真了不起!三角形的面积公式是底×高÷2。
生2:我想把4个图形剪下来,不同形状的图形实际上是两种。我就把这两个图形重叠在一起,多出来(不重合)的部分剪下来,再去拼,看看能不能重合。
师:剪、拼,这样的方法很简便,也很直观。
生3:我可以在图形里打方格,不满半格的算一格,超过一格的也算一格,最后看看方格的总数是不是差不多。
师:你们的想法都非常棒。那就按照你们的想法去试试吧!到底行不行,哪种方法更好,只有动手做,才能得出结论。
5分钟后,集体交流。
生1:我知道底是什么,高就不会量了,所以面积公式知道了也没法求。而且,量到的底也不是整厘米数,小数,分数,都还没有学呢!
生2:剪下来拼一拼的话,不太好剪还容易破碎,但是大致上还是重合的。
生3:打方格太麻烦了,每个方格都要一样大小,这个办法不够简便。
生4:老师,我有一个特别好的方法。我把长方形纸横着对折,再竖着对折.......
师:上台给大家介绍吧!
生4:在原来的基础上,再把长方形的长平均分成2份(取中点),宽也平均分成2份(取中点),这样平均分成8个小三角形,每个小三角形是一样大的。刚刚的4个三角形,每个都由一样大小的两个小三角形组成,所以这4个三角形肯定是相等的。(见图2)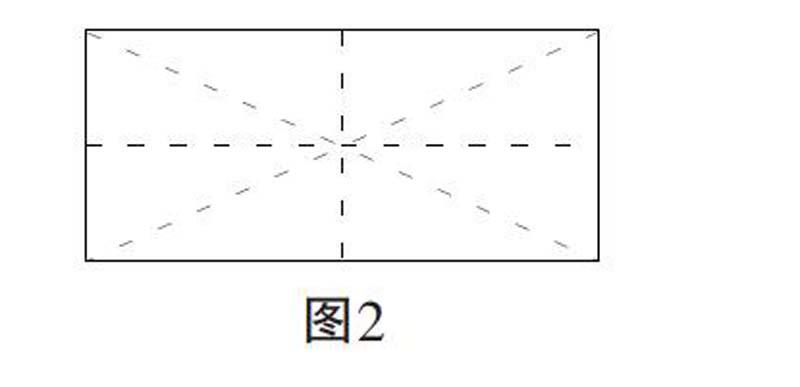
随着生4的讲述,学生频频点头。讲完,全场掌声雷动。
师:这种方法,看懂了吗?
生(齐):看懂了。
师:那么,回到开始的问题,沿着两条对角线折一折,每份是长方形的四分之一吗?
生:是的。
师:为什么?形状不一样啊!
生:形状不一样没关系,只要每份的大小一样,就是平均分。
师:是呀,每份分得同样多,叫做平均分。这里的同样多,只要大小相等就可以了。
二、课后反思
《全日制义务教育数学课程标准》指出:有效的教学活动不能单纯地依赖模仿与记忆,动手实践、自主探索与合作交流是学生学习数学的有效方法。上述教学片断,让学生收获的并不仅仅是“几分之一”的含义。面对出现的新问题,笔者充分引导学生通过自己的方式主动参与探究,旨在关注学生的思维发展,激发学生学习数学的兴趣,提升学生的数学素养。
1. 学会质疑,善于思考
学成于思,思源于疑。思维的活力,永远是从问题开始的。有效的问题牵引着积极的思考不断前行。新课改的课堂上,问题,不一定是教师提出;疑惑,也不一定由教师给出答案。善于质疑的孩子,会有无数个为什么:或对一个现象有疑问,或对一种方法有疑虑,也可能对一段结论有疑窦……在教学片断中,就有孩子主动质疑:“这样(沿着对角线)分是平均分吗?”很真实的问题。书本、练习中出现的平均分,几乎都是分得的每一份大小、形状完全一样,让人一看就能判断是平均分。所以当学生观察到这4份形状不一样时,就自然产生了“形状不一样,大小也不一样”的想法,符合三年级孩子的认知水平。质疑,是因为有思考,有不同思维的碰撞。有质疑,才有进一步的探索和思考。课堂是信息的交流场,无疑处生疑,有难而生疑,鼓励学生敢疑、善思,一定能迸发出有趣的思维火花。
2. 合理猜想,催生智慧
波亚利说:“在数学的领域里,猜想是合理的,值得尊重的。”猜想是一种能力,是一种智慧,是通向结论的必要环节,与猜不同,猜想更侧重于想,即思考,有依据地思考。教学片断中,学生提出的不同猜想,都有自己的判断依据。每一种猜想,都真实反映了学生的知识建构与思维方式。这时,如果打断学生的争辩,舍弃学生的猜想,直接告知学生结论也未尝不可,但是对学生的学习热情是一个很大的打击,也会因此失去一次很好的探究机会。通过引导,通过不同猜想之间的思维碰撞,学生不但知道了多种方法,更理解了平均分的本质:每份分得一样多。这里的“一样多”,并不一定是“形状大小完全相同”,而是“只要每一份的大小一样,就是平均分了”。正因为学生理解了平均分的本质,掌握了分数的含义,才会更加自信、自得。数学学习本应是学生主动建构知识的过程,每个学生对知识都有自己的理解、思考和解决的策略。因此,教师应当营造自由的研究氛围,鼓励学生凭借经验大胆猜想,用不一样的猜想,让问题具有深入探究的价值,催生出更多的数学智慧。
3. 灵活求证,主动探究
一位学者曾说:“一生有用的东西肯定是学生能带走的,因为能带得走,才会对学生一生的发展起作用。带得走的东西,是说它不是停留在书本上,不是停留在教室里,不是还给老师。总之,它不是外在的,而是内化在学生的素质结构里,成为学生的一种素养,是属于学生自己的。”探究,就是这样的一种素质。教学片段中,在猜想过后,学生提出了几种求证的方法:“先算面积,再比一比得数”“剪一剪,再拼一拼看是否重合”“画格子、然后数一数”,这些都是合理的验证方法、可操作的探究思路。发言的几个孩子清楚地表达了探究的意图、不同的验证方法和预期的目标,容易被同龄的小伙伴理解和认可,激起共鸣,灵活选择自己感兴趣的方法去主动探讨,积极验证。在整个验证与探究的过程中,或许还有疑问,也许遇到困难,可能还会有争执,更可能没法达到预期的设想,但是每个人都有主动参与探究的欲望,每个人对探究过程都有自己的期待、思考与见解。学生们乐在其中,弄清了知识发生、发展的全过程,体验到了探究的快乐
综观整个教学片断,最后那位孩子的解答方法无疑是亮点。方法的启迪、认知冲突时的交流、积极探究时的兴致、努力思考时的眼神、同伴介绍方法后的雷鸣掌声……这些孩子共同搭建了一条质疑、猜想、验证结论的有趣的探索之路,谱写了新课程课堂的精彩!
(编辑:赵 悦)
