一类具有结构阻尼的耦合梁方程组的初边值问题

段文梅,张建文

(太原理工大学 数学学院,太原 030024)



一类具有结构阻尼的耦合梁方程组的初边值问题

段文梅,张建文

(太原理工大学 数学学院,太原 030024)

摘要:研究了一类具有结构阻尼的耦合梁方程组的初边值问题,运用Galerkin方法证明了方程组弱解和强解存在的唯一性，以及对初值的连续依赖性。

关键词:结构阻尼；耦合;梁方程组;Galerkin法;初边值问题

对于弹性梁的研究,由于其理论意义的应用背景,受到了广泛关注。BALL[1]研究了具有内外阻尼的梁方程的横向平面运动,建立了如下模型：

运用Galerkin法证明了该方程组解存在的唯一性问题；并且分别运用半离散和全离散时间Galerkin法,给出了该方程组解的稳定性分析和误差估计。其中，ψ(w1,w2,w3)={β+γ(|w1|2+|w2|2)}w3;p,q∈L∞(0,T;L2(Ω));p(x,t)和q(x,t)分别表示y轴和z轴方向所受到的力。笔者在前人的基础上,研究了一类具有结构阻尼的耦合梁方程组,

(1)

(2)

初始条件

(3)

下的适定性问题。其中，

α1,α2,k,δ,γ,σ>0；β无限制。证明了方程组式(1)-式(3)弱解和强解的存在的唯一性，以及对初值的连续依赖性。

1预备知识和记号

首先设定一些符号,并且引入一些函数空间。

X为Banach空间,对于空间Lp(0,T;X),其范数定义如下

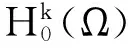
Hk(Ω)的内积和范数定义如下,

式中：|·|表示由内积

诱导的范数。

对于正整数r,函数空间Sr定义如下，

成立。

在证明本文主要结论的过程中,需要下面几个重要引理。

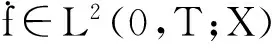
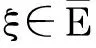
引理2的详细证明见文献[2]。

引理3[2](Gronwall不等式)假设f∈L∞(0,T),K≥0,C0为常数。如果

那么，

f(t)≤C0eKt.

2主要结论

定理1如果u0,v0∈S1(Ω)；u1,v1∈L2(Ω)；p,q∈L∞(0,T;L2(Ω)),则方程组(1)-(3)存在唯一的弱解{u,v},且u,v∈L∞(0,T;S1(Ω))；ut,vt∈L∞(0,T;L2(Ω)).

证明:下面分5步进行证明。

1) 近似解{um,vm}的构造。设，{φj}是S1(Ω)的一组规范正交基，考虑如下方程组

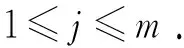
其中：

(8)

在S1(Ω)中 ，

(9)

在L2(Ω)中,

(10)

容易证得这些给定初值条件下的方程组在[0,T]的子区间[0,tm]存在唯一解。

2) 近似解{um,vm}的先验估计。为了证明tm=T独立于m,需要对u和v进行先验估计。

因为

然后在[0,t]上积分,得

因为p,q∈L∞(0,T;L2(Ω)),所以

又因为α1,α2,δ,γ,k,σ>0,所以，

(11)

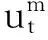
因为，可分赋范线性空间的一致有界线性，泛函序列中必存在一个弱*收敛的子序列,所以可抽取{um}和{vm}的子列{uμ}和{vμ}满足下列性质；

uμ→u,vμ→v，在L∞(0,T;S1(Ω))中弱*收敛；

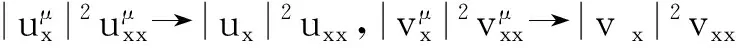
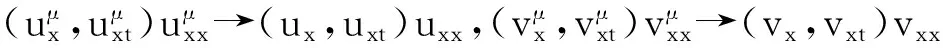
因此,对式(6)和式(7)取极限可得,对于∀φ∈S1,都有式(4)和式(5)成立。

4) {u,v}满足初始条件。因为

uμ→u,vμ→v，在L∞(0,T;L2(Ω))中弱*收敛；

由引理1可得,uμ和vμ几乎处处连续,则对∀φ∈L2(Ω),都有

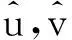
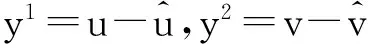
因为

以及

所以,

由引理1和引理3可知,

接下来讨论该问题解的正则性,即得到了该问题的强解。

定理2如果u0,v0∈S2(Ω);u1,v1∈S1(Ω);p,q∈L∞(0,T;L2(Ω)),则存在唯一函数对{u,v},u,v∈L∞(0,T;S2(Ω));ut,vt∈L∞(0,T;S1(Ω));utt,vtt∈L∞(0,T;L2(Ω)),且满足,

以及初始条件

证明:证明过程与定理1类似。

设，{φj}是S2(Ω)的一组规范正交基，近似解{um,vm}的构造如式(8)所示,满足

1≤j≤m .

以及初始条件,在S2(Ω)中,

(14)

在S1(Ω)中,

(15)

式(12)和式(13)中的φj分别用uxxxxt和vxxxxt代替,然后将两式相加,得

在[0,t]上积分得，

因此由式(11)可得，

(16)

如定理1的证明,同样可证得存在唯一的{u,v}，满足方程组(12)-(13)以及初始条件,并且u,v∈L∞(0,T;S2(Ω))；ut,vt∈L∞(0,T;S1(Ω))；utt,vtt∈L∞(0,T;L2(Ω)).

参考文献：

[1]BALL J M.Stability theory for an extensible beam[J].Differential Equations,1973，14(3):399-418.

[2]BALL J M.Initial-boundary value problems for an extensible beam[J].Math Anal Appl，1973，42(1)：61-90.

[3]GEVECI T,CHRISTIE I.The convergence of a Galerkin approximation scheme for an extensible beam[J].Rairo Mathematical Modelling & Numerical Analysis Modelisation Methematique Et Analyse Numerique,1989,23(4):597-613.

[4]WOINOWSKY-KRIEGER S.The effect of axial force on the vibration of hinged bars[J].Appl Mech,1950,17(1):35-36.

[5]CHOO S M,CHUNG S K.Finite element galerkin solutions for the nonplanar scillatory beam equations[J].Appl Math Comp,2000,114:279-301.

(编辑：朱倩)

On the Initial-boundary Value Problem of the Coupled Beam Equations with Structural Damping

DUAN Wenmei,ZHANG Jianwen

(CollegeofMathematics,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Abstract:This paper deals with the initial-boundary value problem of the coupled beam equations with structural damping. We prove the existence,uniqueness and continuous dependence upon data of weak solution and strong solution using Galerkin method.

Key words:coupled; structural damping; beam equation; Galerkin method; initial-boundary value problem

文章编号:1007-9432(2016)02-0270-05

*收稿日期：2015-04-27

基金项目：国家自然科学基金资助项目：基于时滞惯性流形的非线性弹性壳结构动力屈曲研究(11172194)；山西省自然科学基金资助项目(2015011006)

作者简介：段文梅(1990-)，女，山西大同人，硕士生，主要从事无穷维动力系统研究，(E-mail)duanwenmei_tyut@163.com通讯作者：张建文，教授，博士生导师，主要从事无穷维动力系统、非线性动力学研究，(E-mail)zhangjianwen@tyut.edu.com

中图分类号:O175.27

文献标识码:A

DOI：10.16355/j.cnki.issn1007-9432tyut.2016.02.028