基于多普勒信息辅助的小目标跟踪算法研究

赵中兴，司　军，栾铸征

(中国船舶重工集团公司第723研究所，扬州 225001)



基于多普勒信息辅助的小目标跟踪算法研究

赵中兴，司军，栾铸征

(中国船舶重工集团公司第723研究所，扬州 225001)

摘要：针对强杂波环境中的小目标探测问题，提出了一种基于目标多普勒信息辅助的跟踪算法，利用目标与环境杂波多普勒特性的差异来改善数据关联的权值，能够提升对小目标的跟踪性能，并通过数据仿真验证了该算法的有效性。

关键词：小目标；数据关联；多普勒特性

0引言

在现代信息化战争中，无人机、导弹等目标往往以较小的雷达截面(RCS)、较低的高度，快速或者慢速前进以规避搜索雷达的监视，并隐蔽在强杂波背景下发动突然袭击，往往达到意料之外的毁伤效果，给己方设施带来了严峻的挑战。因此，如何有效跟踪强杂波环境下的小目标已成为世界各国的棘手问题。

如何在低信噪杂比条件下稳定跟踪目标也一直是国内外各大科研院所的研究热点[1-2]，通常提升小目标跟踪性能的大多数手段方法都在前端上，例如提高辐射功率、降低接收机噪声系数、增加脉冲积累点数和提高天线增益等，这些方法在很大程度上受到硬件性能、成本、工艺等因素的约束和限制，在实际操作中的可实施性较差。

除了上述这些方法外，国内外学者也在考虑如何从后端信号和数据处理中寻求方法来提高小目标的跟踪性能，这一领域在近年来取得了一定的研究进展，主要集中在检测前跟踪(TBD)算法和知识辅助的跟踪算法[3-5]。

TBD算法在数据处理之前不作恒虚警处理，对原始回波数据平面作多帧积累，这一点与传统的检测后跟踪(DBT)算法大相径庭，其目的是在更高维度的空间内利用目标与杂波噪声的差异将二者分离，能够大大提升小目标的正确跟踪概率，但这种算法的主要缺点是计算量大、实时性差、资源耗费严重，目前世界各国很少有装备采用TBD算法。

知识辅助的跟踪算法是专门针对低信噪比条件下的小目标跟踪而展开的热门研究方向，顾名思义，就是在传统DBT算法中引入知识辅助。传统DBT算法的处理方法是：首先对原始数据平面作恒虚警检测处理，然后进行航迹起始、数据关联和滤波等处理后形成目标航迹。数据关联即点迹航迹关联，在这个过程中，仅利用了量测点迹的位置、状态等信息，忽视了其他有用信息(这些有用信息统称知识)，例如环境杂波特性、目标特性和地理信息等。在虚警概率一定的情况下，存在目标点迹遗漏、杂波点迹较多等现象，导致跟踪性能不佳。知识辅助的跟踪技术正是将知识融入到数据处理中，在一定的概率下区分目标点迹与环境杂波点迹，调整数据关联的参数与结构，达到稳定跟踪的目的。

鉴于知识辅助跟踪的优势，本文提出一种基于多普勒信息辅助的跟踪算法，用来解决强杂波环境下的小目标跟踪问题。

1算法原理与实现

1.1多普勒辅助跟踪算法原理

作为典型的知识辅助跟踪算法，多普勒辅助跟踪算法的实质是在传统的DBT算法处理中引入目标多普勒信息，增强目标数据与环境杂波数据之间的区分度。因为目标的多普勒特性和运动性质有关系，呈现出一定的规律性；但环境杂波的多普勒特性受风向、风速、时间和自身结构等因素影响，杂乱无章，无规律可循。示意图如图1所示。

图1　N帧目标与环境杂波多普勒信息示意图

从图1 中可以看到，帧间环境杂波多普勒信息相关性弱，十分凌乱，而目标多普勒信息相关性强，符合目标运动规律。跟踪的输入是恒虚警检测后的点迹，即源于小目标的正确量测和源于环境杂波的虚假量测所组成的量测集，多普勒辅助跟踪算法的思想是利用环境杂波和小目标的多普勒信息来提高正确量测与航迹关联的概率，在统计意义下解决航迹维持中由于量测来源的不确定性而形成的“估计”问题。

目标跟踪体系包含航迹起始、航迹维持、航迹确认及删除等处理环节。多普勒辅助跟踪算法应用在航迹维持环节，航迹维持包括航迹预测、数据关联和航迹滤波。多普勒辅助跟踪算法的处理方法是通过数学计算获取多普勒似然因子，进而改善数据关联的权值，提高点迹航迹关联的质量。原理框图如图2 所示。

图2　多普勒辅助跟踪算法原理框图

1.2目标运动模型

根据理论分析和工程应用经验，可假定小目标的运动模型是离散时间的线性高斯模型，状态转移方程为：

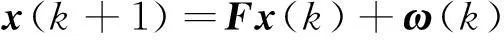
(1)

式中：x(k)为目标在k时刻的运动状态，包含位置、速度以及更多信息；F为状态转移矩阵，描述了目标运动状态从k-1时刻到k时刻的变化规律；ω(k)为状态噪声，用来描述目标运动过程中的各种随机干扰。

为了说明多普勒算法的有效性，本文仅假设一种简单的目标运动模型，即二维平面上的匀速直线运动模型，状态转移矩阵F为：

(2)

状态噪声ω(k)符合零均值高斯分布，其协方差矩阵Q1为：

Q1=E[ω(k)ωT(k)]=

(3)

式中：q为加速度噪声的功率谱密度；T为雷达的扫描周期。

1.3雷达回波测量模型

在雷达的探测过程中，通常可测量获取目标的位置信息，故雷达回波位置测量模型可由如下的观测方程表示为：

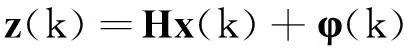
(4)

式中：z(k)为k时刻的观测向量，即包含位置信息的目标量测；φ(k)为k时刻的观测噪声，观测矩阵H为：

(5)

事实上，除了位置信息外，雷达也可获得目标的多普勒信息，故雷达回波测量模型中还包含多普勒观测方程，可表示为：

(6)

式中：r(k)为k时刻的多普勒状态；在匀速直线运动的条件下，观测矩阵Hd=1；n(k)为k时刻的观测噪声。

1.4多普勒辅助概率数据关联(PDA)算法

如1.1节所述，多普勒信息通过改善数据关联的权值来达到辅助跟踪的目的。数据关联算法分为硬关联和软关联2种类型。软关联算法适用于低信杂比条件下的小目标跟踪。PDA算法是最典型的软关联算法，故本文采用多普勒信息辅助PDA算法来实现小目标跟踪。原始PDA算法仅利用回波位置量测完成数据关联，核心思想是根据统计距离计算关联波门内每个量测源自目标的概率，利用概率值对相应的量测值进行加权，计算出一个综合的量测值作为等效回波位置量测值来完成点迹航迹关联[6]。原始PDA算法的假设条件如下：

(1) 每个时刻在跟踪波门内至多只有一个量测值源自目标；

(2) 正确量测值服从高斯分布，虚假量测值服从均匀分布。

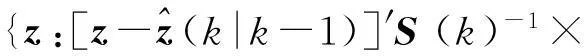
(7)

经计算，公式(7)中波门的体积为：

(8)

式中：nz为量测的维数,nz=1,2,3,…，有Cnz=1,π,4π/3,…。

在PDA算法中，虚假量测数为mk的概率密度函数μF(mk)有参数模型或非参数模型2种形式，本文采用参数模型，即落入波门内的虚警点数服从参数为λV(k)的泊松分布，数学表达式为：

(9)

每个时刻目标的检测概率表示为Pd，源于目标的量测落入跟踪波门内的概率为Pg。经计算，k时刻的mk个位置量测的关联概率为：

(10)

(11)

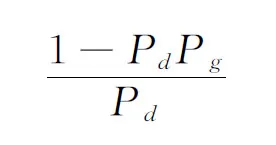
(12)

因此，采用PDA算法计算出的综合回波位置量测值为：

(13)

接下来，利用综合回波位置量测值v(k)完成点迹航迹关联，并采用卡尔曼滤波迭代算法对目标位置信息进行实时更新，进而实现对目标的连续跟踪，具体的算法处理流程如下：

(1) 目标位置状态一步预测：

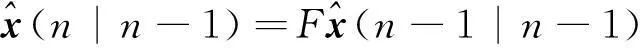
(14)

(2) 根据回波位置量测zi(k)来计算新息过程：

(15)

(3) 目标位置状态一步预测误差的自相关矩阵：

(16)

(4) 新息过程的自相关矩阵：

(17)

式中:观测噪声φ(k)的自相关矩阵为Q2(k)=E{φ(k)φ′(k)}。

(5) 卡尔曼增益：

(18)

(6) 目标位置状态估计：

(19)

(7) 目标位置状态估计误差的自相关矩阵：

P(k|k)=P(k|k-1)-

(20)

(21)

(8) 重复进行步骤(1)～(7)，进行迭代滤波计算。

多普勒辅助PDA算法的原理是计算一个多普勒似然因子(DLF)作为加权值来修正关联概率βi(k)，以增大正确量测的比重，从而提升小目标的跟踪稳定度，首先提出该算法的几个假设条件：

(1) k时刻的多普勒量测zd(k)和位置量测z(k)一一对应；

(2) 倘若k时刻的位置量测z(k)源自某一目标，则同样地，多普勒量测zd(k)也源自该目标；

(3) k时刻的位置量测z(k)与多普勒量测zd(k)相互独立。

在上述的假设条件下，同样地，也通过卡尔曼滤波迭代算法对目标多普勒信息进行更新，实时获得修正后的数据关联概率，多普勒状态噪声、观测噪声的自相关矩阵分别用σs、σd表示，具体的算法流程如下：

(1) 多普勒状态一步预测：

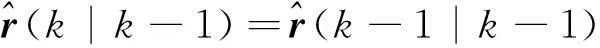
(22)

(2) 新息过程：

(23)

(3) 多普勒状态一步预测误差的自相关矩阵：

(24)

(4) 新息过程的自相关矩阵：

(25)

(5) 卡尔曼增益：

(26)

(6) 多普勒状态估计：

(27)

(7) 多普勒状态估计误差的自相关矩阵：

Pd(k|k)=Pd(k|k-1)-

(28)

(29)

(30)

(8) 重复进行步骤(1)～(7)，进行迭代滤波计算。

那么，修正后的数据关联概率为：

(31)

DLF的数学表达式如下：

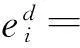
(32)

根据多普勒信息辅助PDA算法的假设条件，多普勒量测zd(k)和位置量测z(k)一一对应,相互独立且来源于同一目标，于是将修正后的数据关联概率值βi(k)应用于计算综合的位置量测值，提高了源于小目标的正确量测的概率值，获得了更加准确的目标位置状态估计。

2数据仿真分析

本节的主要内容是完成基于多普勒信息辅助的小目标跟踪算法性能验证，首先设定仿真条件，模拟强杂波背景下的小目标跟踪场景，然后给出数据仿真结果，并对比多普勒信息辅助算法与传统算法的跟踪性能。

2.1仿真条件

本次仿真中背景杂波起伏模型采用K分布，小目标采用SwerlingII起伏模型，信杂比为9dB，具体仿真参数如表1所示。从2个方面来分析小目标的航迹维持性能：(1)目标位置状态的最小均方根误差(RMSE)；(2)有效跟踪的概率。

表1　仿真参数

在M次蒙特卡洛仿真中，通过计算有效航迹的条数N来获得有效跟踪的概率N/M，航迹有效的定义为：在整个航迹维持的过程中，倘若位置估计误差始终低于门限t1，则该航迹有效；若某一时刻的位置估计误差超过门限t1，继续等待L帧，假设在L个扫描周期内误差下降到t1以下，认为该航迹有效，反之则认定该航迹失效；若某一时刻的位置估计误差超过门限值t2(t2>t1)，则可直接断定该航迹失效。

2.2仿真结果

针对X×Y监视区域内形成的回波数据平面，假定目标初始状态已知，采用传统的DBT算法进行处理，即首先进行单元平均-恒虚警率(CA-CFAR)检测，然后采用卡尔曼滤波算法实现目标跟踪。图3 为2种算法的RMSE曲线对比图，表示在总扫描周期中每一帧航迹的RMSE。图4 为第499次蒙特卡洛仿真中原始PDA算法和多普勒信息辅助PDA算法的处理结果。表2是有效跟踪概率对比表。当然，RMSE越小、有效跟踪的概率越高代表跟踪性能越好。

图3　2种算法的RMSE曲线对比图

图4　2种算法在第499次蒙特卡洛仿真中的建航结果

处理方法传统算法多普勒辅助算法有效跟踪概率0.174 0.805

从图3可以看出，原始算法中有12帧航迹的RMSE超过2.5，而多普勒信息辅助算法中仅有5帧航迹的RMSE超过2。明显地，利用了多普勒信息辅助跟踪算法后，目标航迹RMSE曲线的收敛

性能更佳，数值更小，图4 的建航结果显示在信杂比为9dB的条件下，多普勒辅助跟踪算法的航迹优于原始算法，与目标真实航迹的匹配度更高。从统计意义上看，利用了多普勒信息辅助后，有效跟踪概率大大增加(如表2所示)。

3结束语

本文研究了多普勒信息辅助DBT算法对小目标跟踪性能的影响，数据仿真结果显示这种方法具有良好的数据关联性能，能够大幅改善传统DBT算法对强杂波背景下小目标的跟踪质量。下一步需研究在目标多普勒状态估计误差较大的情况下对跟踪效果的影响，以及多普勒信息辅助跟踪算法对航迹存在交叉的多目标跟踪问题的适应性，为今后的工程化应用夯实基础。

参考文献

[1]张昌芳,杨宏文,胡卫东，等.低数据率条件下的目标跟踪[J].电光与控制,2008,15(7):7-12.

[2]李翠平,毕越凯,孙进平,等.战场监视雷达地面运动目标跟踪方法[J].中国电子科学研究院学报,2010,5(6):638-643.

[3]刘彬.微弱目标检测前跟踪算法研究[D].成都:电子科技大学,2010.

[4]CAPRAROCT,CAPRAROGT,WICKSMC.KnowledgeAidedDetectionandTracking[C]//IEEERadarConference,2007:352-356.

[5]陈振兴.基于知识辅助的弱目标跟踪算法研究[D].成都:电子科技大学,2013.

[6]KIRUBARAJANT,BARSHALOMY.Probabilisticdataassociationtechniquesfortargettrackinginclutter[J].ProceedingsofTheIEEE,2004,92(3):536-557.

Research into Small Target Tracking Algorithm Based on Doppler Information Assistant

ZHAO Zhong-xing,SI Jun,LUAN Zhu-zheng

(The 723 Institute of CSIC,Yangzhou 225001,China)

Abstract:Aiming at the problem of small targets detection in strong clutter environment,this paper puts forward a tracking algorithm based on target Doppler information assistant,improves the weights of data association by using the difference of Doppler characteristics between the targets and environment clutters,which can improve the tracking performance to small targets.The validity of the algorithm is verified through data simulation.

Key words:small target;data association;Doppler characteristic

收稿日期:2015-12-08

中图分类号：TN971

文献标识码：A

文章编号：CN32-1413(2016)02-0005-05

DOI:10.16426/j.cnki.jcdzdk.2016.02.002