负顾客造成服务速率变化的M/G/1可修排队系统研究

裴秀艳　岳德权

(1. 运城职业技术学院基础课教学部, 山西 运城 044000； 2. 燕山大学理学院， 河北 秦皇岛 066004)



负顾客造成服务速率变化的M/G/1可修排队系统研究

裴秀艳1岳德权2

(1. 运城职业技术学院基础课教学部, 山西 运城 044000； 2. 燕山大学理学院， 河北 秦皇岛 066004)

摘要：针对由负顾客到达而引起的服务速率变化情况，研究服务速率可变的MG1排队系统。服务规则假设为FCFS，负顾客的到达一方面移除了正接受服务的正顾客，另一方面使服务台服务速率产生变化。运用补充变量法、状态转移分析法得到稳态下的偏微分方程组，变换求解方程，得到系统在各个状态下的概率表达式及稳态条件下队长母函数的概率表达式。

关键词：负顾客； 可修排队； 补充变量法； 概率母函数

Gelenbe在1991年首次提出了负顾客排队模型[1]，此后关于负顾客排队的研究大量出现。此类模型在实际生活中应用较为广泛，对此类负顾客模型的研究具有实际意义。但各类相关研究的侧重点仅限于负顾客的抵消策略上，而基本没有考虑负顾客对服务台的影响。本次研究将考虑负顾客对服务台的影响，结合服务速率、服务台故障、可修等内容，进一步研究排队问题。

1模型的数学描述

1.1模型假设

(1)该系统包含正顾客和负顾客两类顾客，一个服务台，假设两类顾客分别以λ+、λ-的泊松流到达。负顾客到达后，若服务台处于繁忙期，则会有一名接受服务的正顾客被带走；若服务台处于空闲或故障期，负顾客的到达不会影响服务台工作。

(2)遵循正顾客先到先服务(FCFS)方式，假设以高速率μ1服务时，到达的负顾客带走一位正顾客，同时以概率(1-p)使服务速率由μ1降为μ2(μ1>μ2)，或以概率p导致服务台产生故障；当以低速率μ2服务时，到达的负顾客不仅带走一位正顾客，而且导致服务台产生故障。假设在高速率和低速率服务状态下，正顾客的服务时间遵循G～Gi(t)分布：

(3)服务台出现故障后可立即修理，并达到高速服务。修理故障的时间遵循一般连续型随机变量分布H～H(t)：

1.2系统的状态与概率定义

在t时刻系统中排队的正顾客数令为N(t)，t时刻服务台的状态令为I(t)，定义如下：

显然{I(t),N(t),I(t)=0,1,2,0≤N(t)≤∞}不是马尔可夫随机过程。补充变量X(t),Y(t)：其中X(t)表示t时刻负顾客到来时正顾客已用去的服务时间；Y(t)表示正在被修理的服务台已用去的修理时间。这样，随机过程{N(t)、I(t)、X(t)、Y(t)}就构成向量马尔可夫随机过程。有以下概率定义：

p0(t)=p{I(t)=1,N(t)=0,x=0}

pn(t,x)dx=p{I(t)=1,N(t)=n,

x0

k0(t)=p{I(t)=2,N(t)=0,x=0}

kn(t,x)dx=p{I(t)=2,N(t)=n,

x0

r0(t)=p{I(t)=0,N(t)=0,y=0}

rn(t,y)dy=p{I(t)=0,N(t)=n,

y0

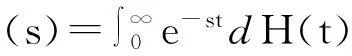
其他符号：

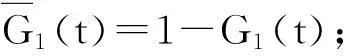
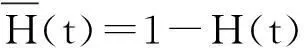
2偏微分方程组及其求解

2.1偏微分方程组

稳态条件下，令t→∞，将上述概率定义为稳态概率：

由状态转移过程，得到系统的状态转移图(图1)：

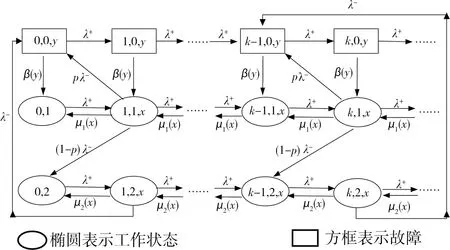
图1　状态转移图

由图1分析得到稳态系统的状态转移方程组：

(1)

(2)

(3)

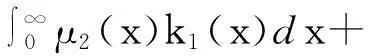
(4)

(5)

(6)

(7)

(8)

稳态下的边界条件：

(9)

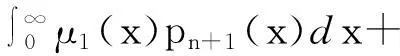
(10)

(11)

(12)

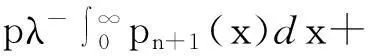
(13)

归一化条件：

(14)

2.2系统稳态方程组的求解

为了求解上述方程，定义下面的母函数：

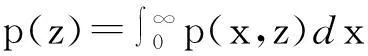
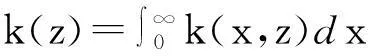
将式(3)两端乘以zn，n≥2，求和，再与式(2)乘以z相加整理可得：

(15)

同理可得：

(16)

(17)

(18)

(19)

将式(13)两端乘以zn，n≥0，求和，整理可得：

(20)

由式(15)可得：

(21)

由式(16)可得：

(22)

由式(17)可得：

(23)

将式(21)和式(23)代入式(18)整理可得：

r(0,z)+λ+p0(1-z)=0

(24)

分别将式(21)、(22)代入式(19)、(20)整理可得：

(25)

(26)

A(z)=λ+(1-z)+λ-

联立式(24)、(25)、(26)，解得：

(27)

(28)

r(0,z)=

(29)

其中：

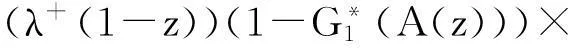
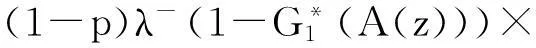
再将式(27)代入式(21)，可得：

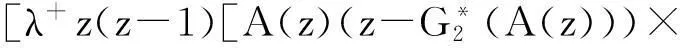
[A(z)B(z)-C(z)〗-1

(30)

同理：

k(z)=[λ+z(z-1)[(1-p)λ-

(31)

(1-H*(λ+(1-z)))]×

[C(z)-A(z)B(z)]-1

(32)

3主要排队指标

(1) 此系统处于空闲期的概率p0：

λ-E(H))][(1-p)λ-×

(33)

(2) 此系统处于稳态时的概率：

(ⅰ) 系统以服务速率μ1为顾客服务的概率：

(ⅱ)系统以服务速率μ2为顾客服务的概率：

(ⅲ)系统故障的概率：

其中：

(ⅳ)系统的稳态可用度：

A=1-pR

(ⅴ)系统的损失率：

Wf=λ-(pμ1+pμ2)

(3)系统稳态队长概率母函数：

L(z)=p0+k0+p(z)+k(z)+r(z)

(4)系统的稳态平均队长为：

此模型中E(L)的一般表达式非常复杂，实际操作时，可根据具体情况先求出p(z),k(z),r(z)的具体表达式，然后再分别求导后令z=1。

4特殊情况

当λ-=0，E(H)=1β=0，p=0时, 对模型中的假设条件进行简化处理，将λ-,μ1,μ2,p,E(H)分别代入L(z)表达式中的各部分，得：

5数值算例

利用Matlab软件作出图形，分析主要参数对该系统队长的影响，从而根据需要改变、调整系统参数，以便达到优化控制的目的。

为了便于分析，在数值计算时，假设修理时间H(t)和服务时间Gi(t)均遵循参数β、 μ1、 μ2的指数分布规律。首先，将参数固定为μ1=1η1=2.0，μ2=1η2=1.0，p=0.5，β=1γ=1.0，正顾客到达率λ+取不同值时，分析负顾客到达率λ-对平均队长产生的影响，参见图2。其次，固定参数λ+=2.0，p=0.5，β=1γ=1.0，服务率μ1、 μ2取不同值，考察不同服务率及负顾客到达率λ-对系统平均队长E(L)的影响，参见图3。

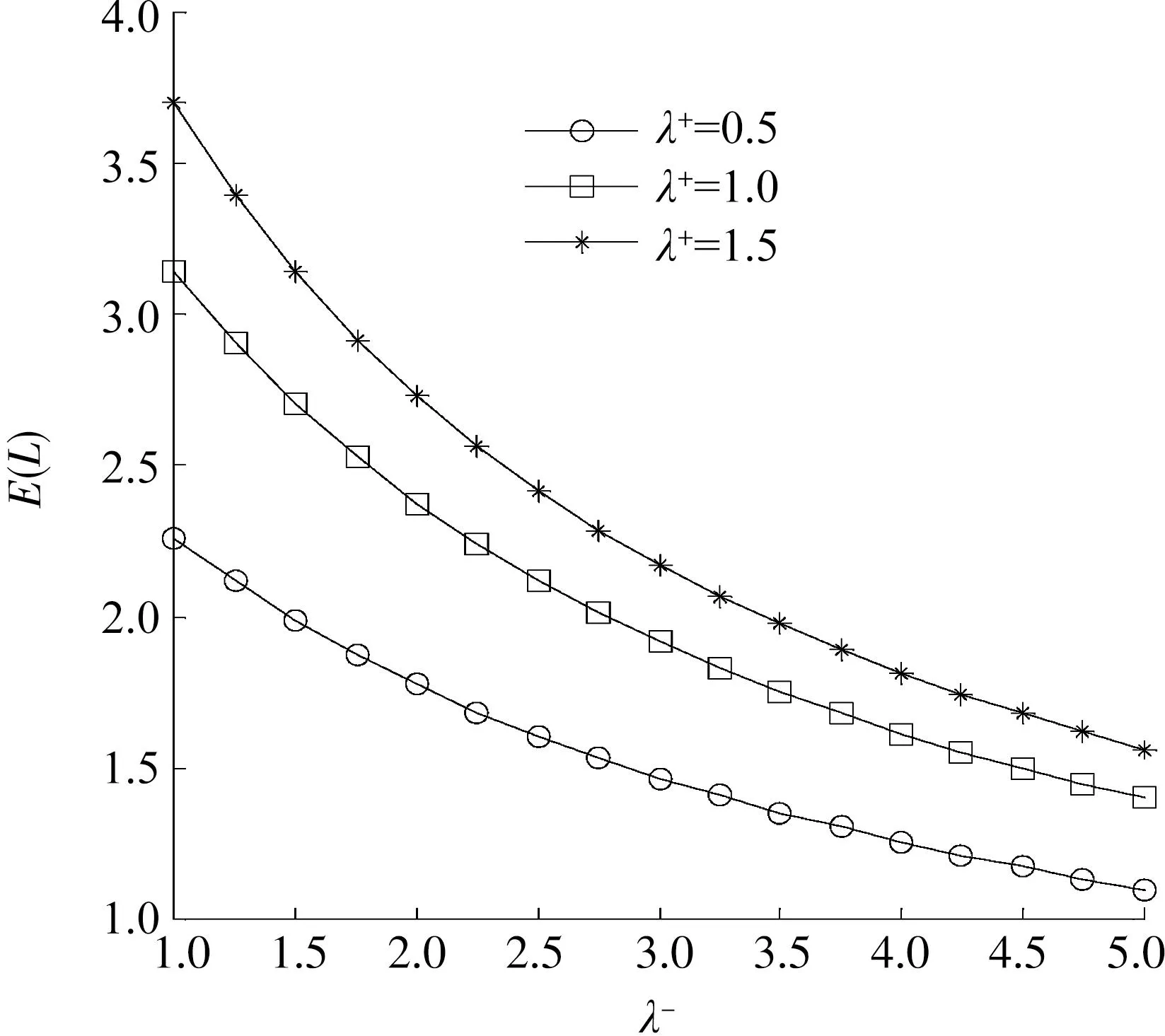
图2　顾客到达率对系统平均队长的影响

由图2、图3观察可得：

(1) 在μ1、 μ2、 β、 p、 λ+固定时，随着λ-的逐渐增大，系统平均队长E(L)逐渐递减；

(2) 在β、 p、 λ+、 λ-固定时，随着服务率μ1、 μ2值增大，系统的平均队长E(L)逐渐递减，且变化趋势相似。

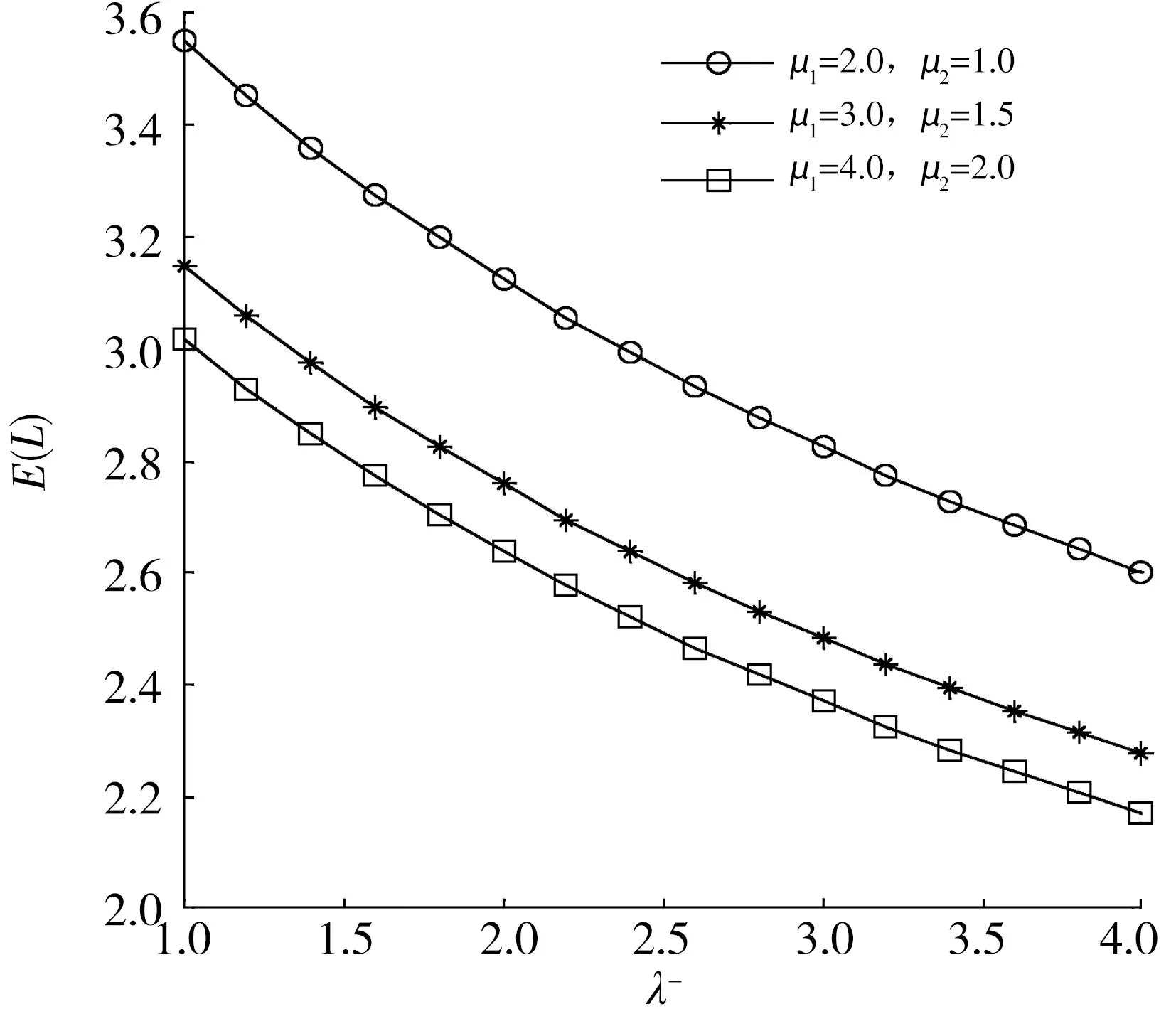
图3　负顾客到达率和服务率对系统平均队长的影响

6结语

本次研究构造了一个新的排队模型，用以研究负顾客到达对服务台产生的影响，该影响体现在服务速率的变化上。运用补充变量法分析状态转移过程，列出偏微分方程组，利用母函数法求解方程，得到了系统的主要排队指标，包括系统处于各状态的概率、队长表达式等。最后，通过数值算例直观地体现主要参数对平均队长的影响，为实际应用提供一些参考。

参考文献

[1] GELENBE E.Queues with Negative Arrivals[J].Appl Prob,1991,28:245-250.

[2] 曲子芳,朱翼隽,杜贞斌.负顾客MG1可修排队[J].江苏大学学报(自然科学版),2003,24(3):20-23.

[3] 陈燕,朱翼隽,陈洋.一类具有负顾客的MG1休假排队模型[J].兰州大学学报(自然科学版),2005, 41(1)：118-121.

[4] 高显彩,朱翼隽.一类带负顾客和反馈的MG1休假排队系统[J].运筹与管理,2010,19(2)：79-83.

[5] 王聚丰,朱翼隽,孙凤欣.服务速率有变化的可修MG(MG)1排队系统[J].兰州大学学报(自然科学版),2003,39(5)：19-24.

[6] 田乃硕.休假随机服务系统[M].北京: 科学出版社,2002：36-82.

Service Rate Changed by Negative Customers inM/G/1 Repairable Queuing System

PEIXiuyan1YUEDequan2

(1. Optometry Department of Yuncheng Polytechnic College, Yuncheng Shanxi 044000, China;2. College of Science, Yanshan University, Qinhuangdao Hebei 066004, China)

Abstract:In this paper, we studied a variable rate of an M/G/1 repairable queuing system, when the service rate changed by the arrival of the negative customer. We assumed the service rules as FCFS, the negative customers′ arrival offset a positive customer who is receiving service, and makes the service rate variable as well. By using the supplemental variable method and state transfer analysis, the partial differential equations was obtained, then solving equations by L-Z transformation; finally the probability of expression in each state and the captain of the generating function of the steady state has been obtained.

Key words:negative customer; repairable queuing system; supplemental variable method; probability generating function

收稿日期：2015-09-15

基金项目：国家自然科学基金项目“具有不耐烦行为和排号机制的排队系统性能分析”(71071133)

作者简介：裴秀艳(1987 — )，女，硕士研究生，助教， 研究方向为排队论。

中图分类号：O 224

文献标识码：A

文章编号：1673-1980(2016)02-0128-05