基于低秩空间的低复杂度干扰对齐算法研究

袁 红 梅

(江苏联合职业技术学院无锡机电分院，江苏 无锡 214028)



基于低秩空间的低复杂度干扰对齐算法研究

袁 红 梅

(江苏联合职业技术学院无锡机电分院，江苏 无锡 214028)

摘要：低秩空间的干扰对齐算法对无线通信网络的干扰抑制效果较好，但因其高复杂度而难以得到广泛应用。针对该算法高复杂度的缺点，提出对干扰系统内所有IA收发滤波并行处理的优化算法，并通过拉格朗日条件极值得到该算法的理论容量上界，最后进行算例仿真对比。结果表明，该优化算法能够在保证网络容量的条件下，降低算法的复杂度。

关键词：干扰对齐； 低复杂度； 网络容量； 低秩空间

随着通信用户数量的激增，用户之间的同道干扰已成为无线通信质量快速发展的瓶颈。干扰对齐(Interference Alignment，缩写为IA)技术为解决此瓶颈问题提供了新的途径，其在干扰信道中具有独特的优越性，可达到干扰信道系统的最高自由度，得到其最大化网络容量。干扰对齐技术的基本原理，首先是在发送端设计预编码器，并利用预编码器处理发送信号，再借助接收滤波器分离出有用信号与干扰信号，进而将有用信号限制在接收信号范围之内，而另一部分干扰信号则被限制在接收信号范围之外，由此实现干扰对齐。

大多数学者的研究对象主要为基于单小区多输入多输出MIMO系统或多小区MIMO系统。有的学者研究了多小区多用户系统的干扰对齐技术，针对该系统的用户数量、天线数目较大的工况，提出新的干扰对齐算法，计算出了系统的最大可达容量[1-4]。有的学者以MIMO系统为研究对象，提出了MIMO X信道的干扰对齐算法，该算法能达到系统的最高自由度[5-6]。有的学者以单小区MIMO系统为研究对象，给出了一种满足该系统干扰对齐技术基本条件的干扰对齐算法[7]。有的学者以基站干扰方式为研究对象，提出了一种新的分布式非线性干扰对齐算法，通过分析迭代方式求解预编码器和接收滤波器，分析小区信道对基站干扰对齐算法的影响[8]。

随着小区数量增多，当用户密集时，算法的复杂度将加大，由此带来的运算高消耗非常不利于算法的实际应用。实现非线性干扰对齐算法的低复杂度优化，是使干扰对齐算法得以广泛应用的关键技术。基于此，本次研究提出一种基于低秩空间的低复杂度干扰对齐算法，并将其应用于无线信号的干扰求解。

1干扰对齐算法的低复杂度优化

首先，为了降低干扰信道中的干扰信号，需要将干扰信号约束在一定空间内，可通过干扰信号矩阵的秩得到最小化系统：

(1)

=conv{rank[blkdiag(I[1],…,I[K])]}

(2)

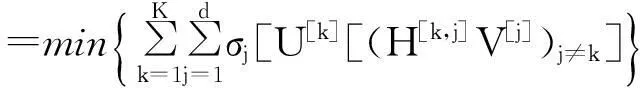
(3)

式中：H[k,j]表示用户j和发送端k之间的信道，其元素满足均值为0、方差为1的复高斯分布；U[k]表示第k个小区内的高斯白噪声，其元素分布满足U[k]～N(0,σ2I);V[j]表示小区j内基站的发送信号;d表示系统最大可用空间。

根据式(3)可以得到干扰矩阵最小的Kd个奇异值之和，进而达到最小化干扰空间的目的。通过对目标函数的优化，只需进行一次干扰对齐处理就能求得所有的预编码滤波器和接收滤波器，这大大节约了算法重复迭代耗费的时间。

为了降低约束条件的复杂度，引入干扰矩阵的凸包络函数，推导出IA约束条件的闭式表达式：

rank(S[k])=rank[U[k]H[k,k]V[k]]

(4)

其有用信号的凸包络函数可表示为：

=conv{rank[blkdiag(S[1],…,S[K])]}

=Kd

(5)

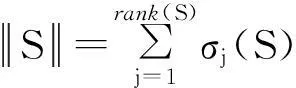
由式(4)、(5)可将干扰对齐算法的模型进一步简化为：

(6)

可见，改进算法对原低秩干扰对齐算法中的目标函数及其约束条件实现了优化。

2最优容量的求解

基于IA模型的式(6)为一个非线性最优化问题，并且满足库恩-塔克(KKT)条件，故可根据拉格朗日条件极值定理求得其最优解。式(6)的目标函数和约束条件可写为：

(7)

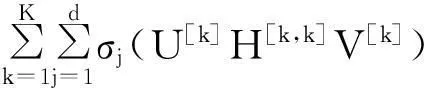
=Kd

(8)

根据拉格朗日函数定义：

L(x1,x2,λ)=f(x1,x2)+λ(g(x1,x2)-c)

(9)

式中：f(x1,x2)为目标函数；g(x1,x2)为约束函数；λ为拉格朗日乘子。

构造式(6)的拉格朗日方程为：

(10)

对式(10)的各个变量求偏导数，可得到海瑟矩阵行列式：

(11)

若|H|>0，且矩阵中各个元素都大于零，则(U[i],V[i])为极小值点，此时网络容量达到其理论上限。

3仿真结果分析

为了验证所提算法的有效性，在此以多小区通信系统为研究对象，分别仿真计算出多小区通信系统理论容量，从而对比分析出优化前、后IA算法的性能。仿真算例具体参数如下：选取7个小区，每个小区的用户数量为2，算法的迭代次数分别设置为1和100，仿真结果如图1和图2所示。

图1和图2的通信系统自由度分别为3和4，收发天线分别为4×4和8×4。其中，IA表示原干扰对齐算法的网络容量，opt-IA代表优化之后的干扰对齐算法的网络容量，up-bound of opt-IA代表优化后干扰对齐算法的理论网络容量上界。

图1　多小区网络容量仿真图(一)

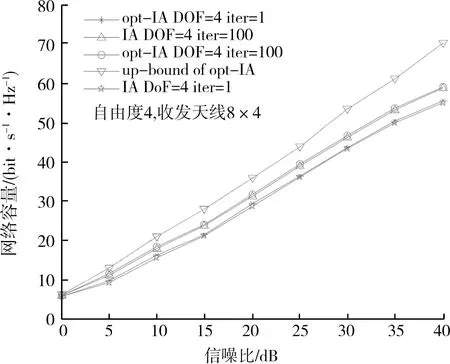
图2　多小区网络容量仿真图(二)

表1所示为优化前、后运行时间。当系统的自由度相同且算法迭代次数一致时，应用优化前、后的算法分别计算系统运行时间。

表1　系统优化前、后运行时间　s

通过以上对比可知，干扰对齐算法在经过低复杂度优化后，大大缩短了计算时间，而且优化后的算法降低干扰网络自由度。

4结语

本次研究针对干扰对齐算法特性，引入凸包络函数，对系统中所有的编码矩阵进行初始化，并计算出系统的接收滤波矩阵，实现了干扰对齐算法的低复杂度优化，解决了非线性干扰对齐算法复杂度过高的问题。通过拉格朗日非线性方程的条件极值计算方法，推导出了该干扰对齐算法的理论网络容量上界，给出了该算法的最优容量，对算法的实际应用有一定的指导作用。

参考文献

[1] CADAMBE V R, JAFAR S．A．Interference Alignment and Degrees of Freedom of the K-User Interference Channel[J].IEEE Transactions on Information Theory，2008，54(8):3425-3441.

[2] YU H, PAKR J, SUNG Y, et al. A Least Squares Approach to Joint Beam Design for Interference Alignment Inmultiuser Interference Channels[J].IEEE Trans on Signal Proc, 2010, 58：4960-4966.

[3] PETERS S W, HEATH R W. Cooperative Algorithms for MIMO Interference Channels[G].ARXIV:1002.0424V2, 2010.

[4] 朱斌，葛建华，孙垂强. 多小区干扰对齐的低复杂度发射天线选择算法[J].西安电子科技大学学报，2014，41(2):9-14.

[5] JAFAR S ， SHAMAI S. Degrees of Freedom Region for the MIMO X Channel[J].IEEE Trans on Inform Theory, 2008, 54: 151-170.

[6] 高慧，周欣瑞，吴仁铭，等. 多用户MIMO系统中一种自由度分配算法[J].计算机工程，2015，41(1):71-81.

[7] TRESCH R，GUILLAUD M，RIEGLER E． On the Achievability of Interference Alignment in the K-User Constant MIMO Interference Channel[G].IEEE Workshop on Statistical Signal Processing，2009.

[8] GUPTA P, KUMAR P R. Towards an Information Theory of Large Networks: an Achievable Rate Region[J].IEEE Transactions on Information Theory, 2003，49(8):1877-1894.

Research on Low Complex Interference Alignment Algorithm Based on the Low Rank Space

YUANHongmei

(Electromechanical Vocational and Technical School, Jiangsu Union Technical Institute, Wuxi Jiangsu 214028, China)

Abstract:Interference alignment algorithm based on the low rank space is very meaningful for heterogeneous network. However, its high complexity makes it difficult to obtain a wide range of practical applications. In order to reduce the complexity of the algorithm, this paper proposes all IA transceiver interference filtering system within parallel processing optimization algorithm, and obtains theoretical capacity of the algorithm boundaries by Lagrange Extreme conditions. Finally, it also conducted numerical simulation examples comparison. The results show that the optimization algorithm can ensure the system capacity under conditions and achieve low complexity algorithm.

Key words:Interference Alignment; low complexity; network capacity; low rank space

收稿日期：2015-11-10

基金项目：江苏省高校品牌专业建设工程资助项目“基于3G技术的高职电子技术课程移动学习策略研究”(22700)

作者简介：袁红梅(1979-)，女，淮安人，讲师，研究方向为电子与通信。

中图分类号：TN911

文献标识码：A

文章编号：1673-1980(2016)02-0117-04