生猪养殖环境监测多传感器数据融合模型研究

  钟 旭，江 文，朱幸辉（湖南农业大学信息科学技术学院，湖南 长沙 410128）



生猪养殖环境监测多传感器数据融合模型研究

钟 旭，江 文，朱幸辉
（湖南农业大学信息科学技术学院，湖南 长沙 410128）

摘 要：近年来，随着国家农业信息化进程的不断推进，在农业领域应用多传感器数据融合技术越来越受到学者们的重视。生猪养殖是湖南省的传统优势产业，研究生猪养殖环境监测多传感器数据融合技术，有利于提高我省生猪养殖的信息化、科学化水平。本文以对生猪养殖环境的监测为研究背景，对猪舍中温度、湿度、氨气浓度、二氧化碳浓度进行实时监测，利用提出的两级多传感器数据融合模型对观测数据进行融合，最终得到对实验猪舍实际情况的综合判断，并给出相应的环境调控意见，保证生猪能在适宜的环境中成长。

关键词：多传感器；数据融合；模糊集； DS证据理论；生猪养殖

将数据融合技术应用在生猪养殖环境监测中，提高了系统的稳定性，能得到比单传感器监测更为精确的结果。模糊理论中，隶属度表示论域中一个元素属于某一特定类的程度，该定义与DS证据理论中基本概率分配函数的定义颇为类似。本文探讨的两级多传感器数据融合模型考虑利用隶属度函数来计算基本概率分配函数，并提出了计算证据间融合度作为基本概率分配函数的权重。利用DS证据理论进行融合时，通过引入Jousselme距离改进冲突衡量因子，把证据间的冲突按照比例分配给辨识框架中的元素，得到最终融合结论，通过实验证明了该融合模型的有效性。

1　两级数据融合模型

针对生猪养殖环境的测检测，设计两级数据融合模型，第一级对传感器所得到的原始数据进行初步处理，并定义最优融合集，筛选出相对精准的有效数据，第二级首先利用计算模糊隶属度的方法计算基本概率分配函数，然后使用改进的DS证据理论对证据进行融合，得出最终对养殖环境状态的判定决策。生猪养殖环境多传感器数据融合两级模型如图1所示［1］。

图1　生猪养殖环境多传感器数据融合两级模型

一级融合：首先考虑到传感器可能由于本身构造及环境因素的影响而导致读取数据不准确、偏差较大，若对不精确的数据直接进行融合可能导致最终错误的决策。设计第一层数据预处理，计算传感器观测值之间的绝对距离，并通过专家经验得到绝对距离变化的正常范围，在短时间测算范围内判定读数不稳定的传感器无效，定义最优融合集，进一步缩小融合数据的范围，在减小计算量的同时提高融合精度。得出最优融合集后，对传感器之间的相容度进行计算，给各传感器分配权重，对同类观测值作数据级融合。

二级融合：由于DS证据理论有较好的处理不确定、不完整信息的能力，不需要目标先验概率，能将目标与识别框架中信息转化为数学模型进行，且能通过证据区间的支持情况描述模糊问题［2］，考虑使用DS证据理论进行融合。而DS理论本身在处理数据时存在的各种不足之处，本文针对基本概率分配函数主观性问题，利用计算模糊隶属度的方法计算基本概率分配函数；针对证据高度冲突下融合结果不合理问题，本文改进冲突因子，减小冲突对最终决策的影响。

2　第一级融合算法

利用模糊集理论进行第一层融合是为了将传感器得到的数据进行筛选并进行数据级融合，以保证第二层融合的精确度。因此，本层融合的目的是得到一个传感器读数有效值邻域，并通过判断传感器的稳定性及传感器之间的融合度来确定单个传感器的权重。

考虑到在实际生猪养殖监测中可能存在传感器失效的问题，得出的观测数据直接进行融合可能会影响结果的精度，故在文献［3］最优融合集的基础上进行改进。由于在较短的时间内传感器的观测数据不会有太大的变化，则先利用观测绝对距离对传感器观测数据进行判断。

根据专家一般经验，在T=|tp-tq|（p，q ∈［1，n］）时间段内，传感器观测值变化绝对距离Dt=|Si（tp）-Si（tq）|变化不会超过一定范围。一定间隔时间内各环境影响因子观测值绝对距离变化正常范围如表1所示。

表1　间隔5 s内各环境影响因子观测值绝对距离变化范围

若Dt不在变化正常范围内，则判定此传感器失效，将传感器的权重系数设置为0；若Dt在正常范围内，则判定该传感器有效。

对于有效的传感器，其观测值可能会因为环境噪声、传感器本身精度等因素的影响，导致数据观测偏差较大。可通过计算在t时刻各传感器观测值的绝对距离大小，进一步缩小样本范围，提高融合精度。

设所有传感器在t时间点的观测数据为Si（t）（i∈［1，n］），则传感器之间的观测绝对距离为：

t时刻传感器之间的观测绝对距离Dij（t）构成矩阵：

定义Ω为最优融合集，Ω满足公式（2）所示的条件：

得出的最优融合集即为经过数据筛选后的数据融合样本集合。

计算最优融合集内传感器的权重需要考虑传感器本身的稳定性及当前时刻各传感器之间观测值的相容性。通过计算较小时间间隔内Si（tn） （i∈［1，n］）的方差，可判断传感器本身的稳定性。

利用对数函数来进行转换，将传感器之间的相容性映射到［0，1］区间内。由于考虑到最优融合集中观测数据差距较小，利用对数函数转换后的结果可能为负数，受平面几何中求两点之间距离公式的启发，将观测数据平方扩大后相减。

定义传感器相容度为cij（t）：

根据公式（3），Si（t）与Sj（t）的差值越大，则cij（t）越小，说明相容度越小，相容性差。t时刻传感器之间相容度构成矩阵：

定义传感器的一致融合度为Ci（t），表示在t时刻单个传感器与其他传感器观测数值的融合程度：

在t∈［tp，tq］时间段内，有效传感器观测了m个在最优融合集中的数据，定义单个传感器观测值的稳定度σi：

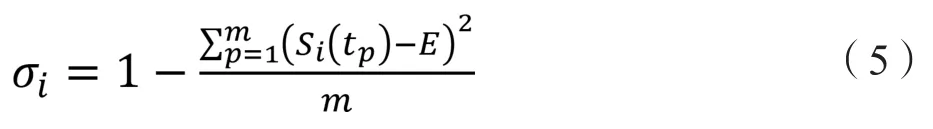
其中，E为t∈［tp，tq］时间段内，Si（tp）的平均数：

在实际情况中，若Ci（t）越大（即：传感器之间融合度高，观测数据接近），且σi越大（即：在一个较小时间段内单个传感器稳定性好，观测数据波动小），则认为该传感器观测数据越可信，应分配较大权重；若Ci（t）越小，且σi越小，则认为该传感器观测数据越不可信，应分配较小权重。

根据上述分析，定义权重wi，并进行归一化处理：

给各传感器分配权重后即可进行融合，融合公式如下：

第一层数据级融合是针对同类传感器的融合，将多个时间点采集的传感器观测数据融合成一个与实际情况最为接近的数据，为第二层决策级融合做准备。

3　第二层融合算法

应用DS证据理论的困难就在于如何将目标数据及原始数据转换为可以进行推理的基本信任分配函数值［4］。模糊集理论中，隶属度函数A（x）取值在［0，1］内，用于表示x属于A的程度，与基本概率分配函数的作用类似，根据DS证据理论中关于信任程度的区间划分，证据的拟信区间包括支持区间与不确定区间，考虑通过使用模糊隶属度函数来计算证据属于支持范围的隶属度与属于不确定区间的隶属度，将两者相加，初步得到DS理论中的基本概率分配函数。再利用证据间距离公式计算证据融合度，对初步的基本概率分配函数进行加权平均，得到新的基本概率分配函数。

根据正态型模糊分布函数的表达式，确定隶属度函数的表达式为：

其中，Six为第i组传感器组所观测到的某个环境因子的观测值（温度、湿度、氨气浓度、二氧化碳浓度），θ为辨识框架中相应环境影响因子的特征值（包括：支持的特征值、不确定的特征值），σ为第i组传感器中相应环境影响因子传感器的特征最大偏差。

分别将每组传感器组中温度、湿度、氨气浓度、二氧化碳浓度隶属于辨识框架中每一焦元的信任隶属度求出后相加，然后对这几组数据进行归一化处理，即可得到初步的基本隶属度函数。

得出初步的基本概率分配函数反映了数据级融合结果对辨识框架中各命题的支持程度，同时，还需要考虑证据之间的支持程度。对于传感器观测到的数值所代表的证据应该被赋予不同的权重，如果一个证据被其它证据所支持，则该证据比较可信，应该赋予较大的权重值，对最终融合结果的影响应该加大［5］。由于基本概率分配函数是DS证据理论考虑信任度的关键所在，故考虑将权重体现在基本概率分配函数上，通过计算证据间的融合程度来给证据分配权重。

定义证据融合度为dij，且满足公式4-10［6］：

其中，i，j=1，2，…，n，A，B∈Θ。

根据公式，mi（A）与mj（B）的差值越大，dij则越小，说明证据间融合程度越小，融合度越差。将证据间融合度全部计算出来则构成融合度矩阵：

融合度矩阵中第i行的数值之和表示第i个证据与其它证据的支持程度，定义证据的支持程度为supi，且满足公式（11）：

计算完证据的融合度后，将融合度进行归一化处理，将归一化处理后的融合度w（supi）作为权重，对基本概率分配函数进行重新分配：

由于各证据基本概率分配函数之和应为1，故应对重新分配的基本概率分配函数再次进行归一化处理，如公式（13）所示：

对于DS证据理论的改进，能准确衡量证据冲突是采用证据法合成冲突证据的前提。DS合成规则中冲突因子k将待合成证据间相交为空的焦元基本概率分配函数乘积之和来表示冲突，但当两焦元相交不为空且非完全相同时，用该方式计算的冲突因子则认为此种情况两焦元不存在冲突，这显然是不合理的［7］。因此考虑对DS合成规则中冲突因子进行改进。

研究领域普遍采用Jousselme距离和Pignistic概率函数进行改进，但实验表明［8］，当针对不同类别的证据时，即证据间完全冲突，利用这两种距离求算方式得出的距离并非为最大值，对证据体之间的距离描述不够准确。

针对Jousselme距离在表示证据距离时存在的问题，对Jousselme距离公式：

进行分析，Jousselme距离之所以不能正确衡量证据差异性的原因在于该公式中常数1/2的取值不当［9］，分母应与m1，m2的取值有关，而不是简单设置为一个常数。m1，m2均为证据所对应的基本概率分配函数，故：m1，m2∈［0，1］，经分析得到，式中分子的范围也应在［0，1］范围内，即：

最终距离d（m1，m2）∈［0，1］的条件即为：分母的结果应大于2。考虑计算证据间距离应与证据对应的基本概率分配函数m1，m2的差值及内积有关，故应在分母部分考虑基本概率分配函数的内积。

本文提出一种对Jousselme距离的改进方式，如公式（14）所示：

综合提出的Jousselme距离的改进公式，及国内外学者的研究成果，考虑到将两个因子相乘可能导致衡量片面性的问题，故采用相加的方式来作为冲突衡量方式，考虑到冲突因子范围应在［0，1］内，故将相加之后的和除2进行归一化处理。表达式如公式（15）所示：

4　实验验证

研究的实验猪舍位于湖南省岳阳市屈原管理区生猪养殖示范基地的生猪人工气候室，内设有生猪产房、保育舍及育肥舍，每间猪舍长度、宽度、高度分别为3.04、2.84和3.16 m。采用BMW-RHTA-S分体型温湿度变送器采集温度、湿度监测环境数据，利用BMG-CO2-NDIR防护型二氧化碳传感器监测二氧化碳浓度，MIC-800-NH3智能氨气检测仪监测氨气浓度。实验主要针对生猪养殖环境中温度、湿度、氨气浓度、二氧化碳浓度进行监测。在猪舍中共设置五组传感器组，分别位于猪舍的四个角及正中央。考虑到传感器本身的质量不稳定因素，将每组传感器组设置实验组、备用组。实验组和备用组中都包含有3个传感器：温湿度传感器、氨气检测仪、二氧化碳检测仪。

为验证两层数据融合模型的融合效果，在试验猪舍进行实验。观测猪舍2015年3月的环境数据，每10 min记录一次数据。从中随机选取2个时间点的数据进行融合。抽取的数据如表2、表3所示。表中Corner1～4表示位于猪舍四角的传感器组，Corner0表示位于猪舍中央的传感器组，Sensor1～4（A）表示实验组的传感器，Sensor1～4（B）表示备用组的传感器。

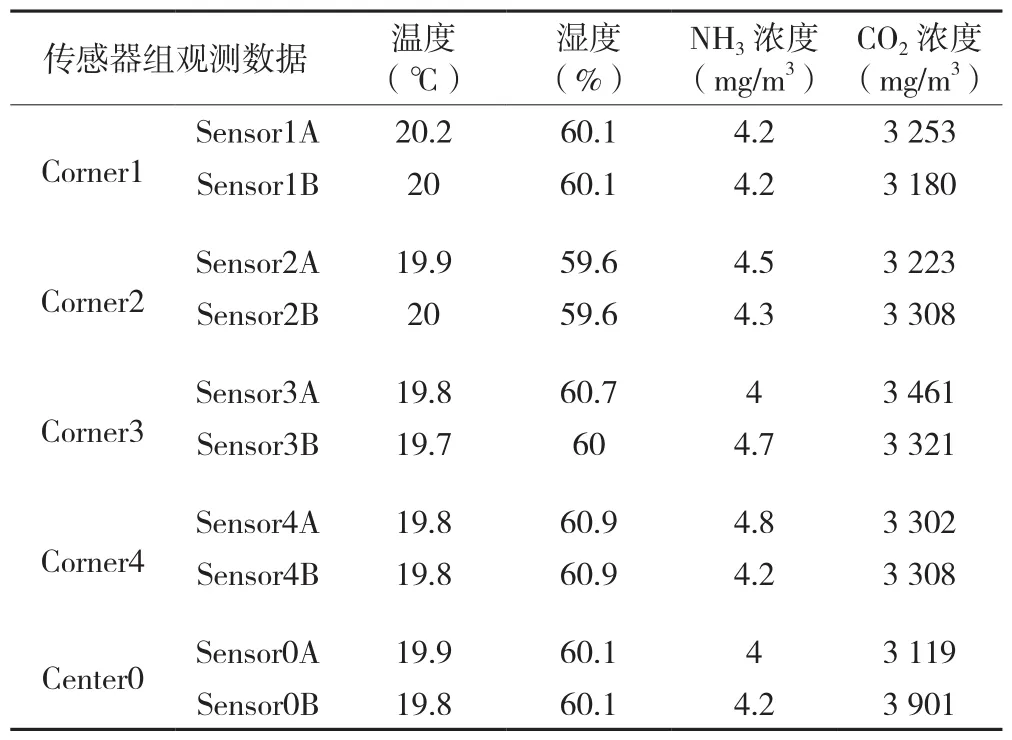
表2　2015年3月7日11： 05观测数据

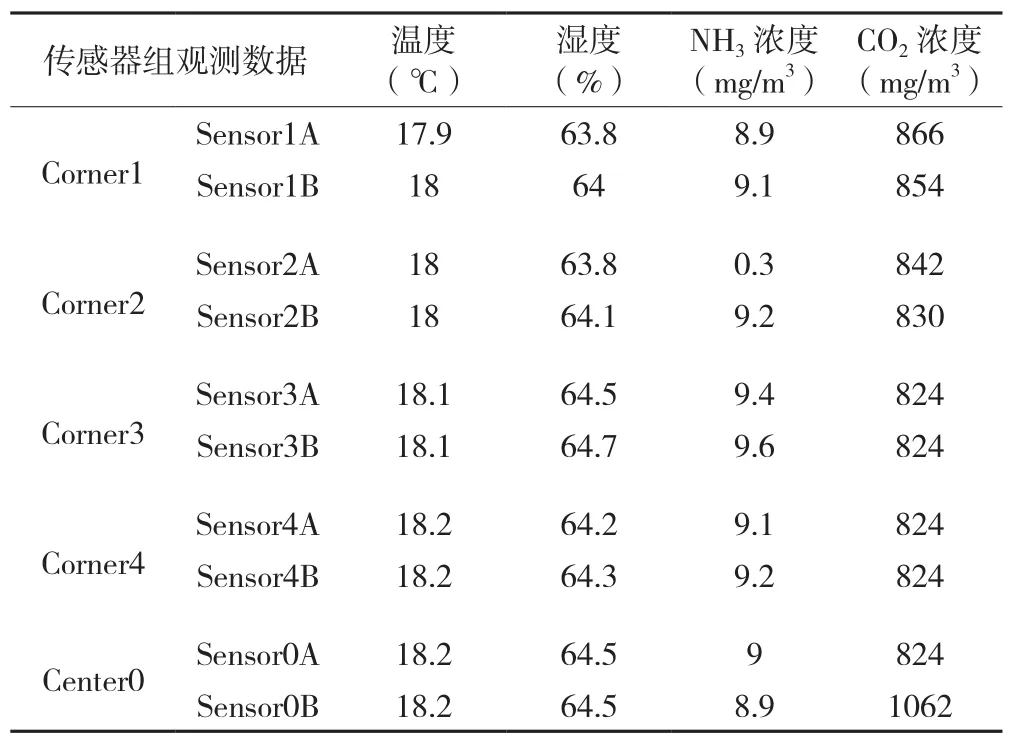
表3　2015年3月14日12： 30观测数据

为了判断传感器的有效性，按要求应观测间隔5 s的观测数据。考虑到要减少环境本身的变化对传感器有效性判断的影响，故需保证环境中各因子的稳定。生猪在夜晚睡觉一段时间后环境中各因子相对处于平稳水平，在2015年3月1日凌晨0点，对5 s间隔内的数据进行采集，结果如表4所示。其中，tq表示tp时刻的后5 s时刻。

参照表1的专家经验，可判断实验组的Sensor2A氨气传感器、备用组的Sensor0B二氧化碳传感器观测值变化剧烈，认定实验组Sensor2A氨气传感器及备用组的Sensor0B二氧化碳传感器为失效传感器。在下一步的计算中，将备用组Sensor2B的氨气传感器数值作为Corner2的观测值，其他仍然用实验组传感器观测值进行计算。

计算出最优融合集后，对集合中的传感器分配权重，最终得出第一层数据级融合的结果为：2015年3月7日11： 05融合的温度、湿度、氨气浓度、二氧化碳浓度分别为：19.8℃、60.2%、4.1 mg/m3、3 295 mg/m3；2015年3月12日12： 30融合的温度、湿度、氨气浓度和二氧化碳浓度分别为18.1℃、64.2%、9.1 mg/m3和825.1 mg/m3。

参照农业部颁布的畜禽场生态环境质量标准NY/ T 388-1999的要求，仔猪猪舍的温度需为27～32℃，相对湿度不超过80%，成猪则为11～17℃和80%；猪舍区氨气浓度不超过25 mg/m3，二氧化碳浓度不超过1 500 mg/m3［10］。

实验猪舍中的猪为成猪，参照标准中对成猪生长环境的要求及观测的数据特点，构造辨识框架为：Θ=｛δ1，δ2，δ3，δ4，δ5，δ6，δ7，δ8｝，其中：

δ1=｛温度合适，湿度合适，氨气浓度合适，二氧化碳浓度合适｝；

δ2=｛温度合适，湿度合适，氨气浓度合适，二氧化碳浓度偏高｝；

δ3=｛温度合适，湿度偏高，氨气浓度合适，二氧化碳浓度合适｝；

δ4=｛温度合适，湿度偏高，氨气浓度合适，二氧化碳浓度偏高｝；

δ5=｛温度偏高，湿度合适，氨气浓度合适，二氧化碳浓度合适｝；

δ6=｛温度偏高，湿度合适，氨气浓度合适，二氧化碳浓度偏高｝；

δ7=｛温度偏高，湿度偏高，氨气浓度合适，二氧化碳浓度合适｝；

δ8=｛温度偏高，湿度偏高，氨气浓度合适，二氧化碳浓度偏高｝；

计算基本概率分配函数及冲突因子后，利用DS合成规则进行计算，得出的第二层融合结果见表5和表6。

表4　5 s间隔内环境各因子变化情况

表5　2015年3月7日11： 05实验融合结果

表6　2015年3月12日12： 30实验融合结果

由2015年3月7日11：05时刻的实验融合结果数据表5可以看出，融合后的概率分配值重新进行了分配，并逐渐向δ6积累，表示辨识框架中δ6的描述与实际情况最相符，即：温度偏高、湿度合适、氨气浓度合适、二氧化碳浓度偏高。根据第一层融合的数据级融合结果进行判断，该结果判断是正确的，研究探讨的两级数据融合模型是可行的，此时应针对该猪舍进行降温、降二氧化碳浓度的处理。

由2015年3月12日12：30时刻的实验融合结果数据（表6）可以看出，融合后的概率分配值重新进行了分配，并逐渐向δ5积累，表示便是框架中δ5的描述与实际情况最相符，即：温度偏高、湿度合适、氨气浓度合适、二氧化碳浓度合适。根据第一层融合的数据级融合结果进行判断，该结果判断是正确的，此时应针对该猪舍进行降温处理。

5　结 论

研究以生猪养殖环境的监测为背景，利用最优融合集筛选出有效观测数据；用模糊集中模糊隶属度函数来求基本概率分配函数，并利用证据间的距离公式计算证据融合度作为证据的权重值分配给基本概率分配函数，减少冲突证据对结果判断的影响。引入Jousselme距离，改进了DS合成规则中的冲突衡量因子，将冲突证据再次进行分配，使概率进一步向最终判断结果焦元累积。对探讨的两级多传感器数据融合模型进行了实验验证，实验得出了对猪舍环境的准确判断，证明了该两级数据模型的有效性，能保证生猪能在适宜的环境中成长，对于有效降低生猪患病率有较大帮助。

参考文献：

［1］ 张河翔. 信息融合技术在煤矿安全监控中的应用研究［D］. 重庆大学，2012.

［2］ 王 力. 基于DS证据理论的多传感器数据融合算法研究与应用［D］. 太原理工大学，2015.

［3］ 杨国宁. 基于模糊集与统计理论的多传感器数据融合算法研究［D］.太原理工大学，2013.

［4］ 宋秀峰. 海洋水质检测系统中多传感器数据融合技术的研究［D］.燕山大学，2013.

［5］ 白剑林， 王 煜. 一种解决 DS 理论证据冲突的有效方法［J］. 系统工程与电子技术， 2009（9）： 2106-2109.

［6］ 陈一雷，王俊杰. 一种DS证据推理的改进方法［J］. 系统仿真学报，2004，16（1）： 28-30.

［7］ 邢晓辰，蔡远文，李 岩，等. 一种改进的证据冲突衡量因子［J］.电讯技术， 2015，55（11）： 1225-1231.

［8］ Liu Zhun-ga， Dezert J， Pan Quan， et al.. Combination of sources of evidence with different discounting factors based on a new dissimilarity measure［J］. Decision Support Systems，2011， 52（1）： 133-141.

［9］ 彭 颖，胡增辉，沈怀荣. 一种修正证据距离［J］. 电子与信息学报，2013，7：1624-1629.

［10］ 李江华. 关于畜禽场环境质量及卫生控制的标准［J］. 肉类研究，2013，5：3-4.

（责任编辑：贺 艺）

Multi-Sensor Data Fusion Models for Monitoring Pig Breeding Environment

ZHONG Xu，JIANG Wen，ZHU Xing-hui
（College of Information Science and Technology， Hunan Agricultural University， Changsha 410128， PRC）

Abstract：In recent years， with the advancement of agricultural informationization process in China， researchers have paid more and more attention to the application of multi-sensor data fusion technology in agricultural area. Pig breeding is the traditional superior industry of Hunan province， and studying the multi-sensor data fusion technology of monitoring pig breeding environment is helpful to improve the informationization and scientific level of pig breeding in Hunan province. Based on the background of monitoring pig breeding environment， the study conducted real-time monitoring of temperature， humidity， ammonia and carbon dioxide concentration in the piggery. It used the proposed two-stage multi-sensor data fusion model to process the observed data， obtained a synthetic judgment on the actual situation of the experimental piggery， and provided relevant environmental regulatory suggestions to ensure that pigs could live in an appropriate environment.

Key words：multi-sensor； data fusion； fuzzy set； DS evidence theory； pig breeding

中图分类号：TP14

文献标识码：A

文章编号：1006-060X（2016）03-0090-06

DOI：10.16498/j.cnki.hnnykx.2016.03.027

收稿日期：2016-01-28

基金项目：国家科技支撑计划（2013BAD15B02）

作者简介：钟 旭（1991-），女，湖南长沙市人，硕士研究生，主要研究方向为多传感器数据融合。

通讯作者：朱幸辉