磁约束聚变等离子体的大规模回旋动理学模拟

肖　湧

(浙江大学 聚变理论与模拟中心，浙江 杭州 310027)



磁约束聚变等离子体的大规模回旋动理学模拟

肖湧

(浙江大学 聚变理论与模拟中心，浙江 杭州 310027)

【摘要】文章介绍了磁约束核聚变能源科学及其密切相关的聚变等离子体物理，以及研究磁约束聚变等离子体非线性物理所必需的大规模回旋动理学模拟的方法及其前沿进展.

【关键词】等离子体；核聚变；磁约束；大规模数值模拟；回旋动理学

1聚变能源科学

1.1聚变能源

核聚变能源是资源取之不尽、清洁的理想能源，将彻底解决人类社会能源问题.如图1，太阳通过氢原子聚变生成氦原子释放能量，在太阳核心部位，每秒钟约有6.2亿吨的氢原子发生聚变反应. 核聚变能源具有以下几个特点.

1.1.1能量巨大

核能是能量巨大的能源，一次核反应释放的能量是MeV量级，而平时我们广泛使用的煤、石油、天然气等化石能源涉及的是化学反应，释放的能量是eV量级，只有前者的千分之一.核能有重核裂变和轻核聚变两种方式，其中核聚变比核裂变释放出更多的能量.例如，铀235的裂变反应，将千分之一的物质变成了能量；而氘的聚变反应，将近千分之四的物质变成了能量.

1.1.2资源丰富

重核裂变使用的主要原料是铀，目前探明的储量仅够使用约1 000年；而轻核聚变使用的燃料是海水中的氘，1升海水能提取30毫克氘，在聚变反应中能产生约等于300升汽油的能量，即“1升海水约等于300升汽油”，地球上海水中就有45万亿吨氘，足够人类使用百亿年.聚变所需的另外一种燃料是氚，在地球上储量并不多，但是可以通过锂转变获得，而地球上尤其是月球上都有大量的锂矿.一旦氘氚聚变实现商用，我们也可以采用其他聚变过程.总之，聚变能基本可以算是取之不尽的能源.

1.1.3成本低廉

1千克氘的价格只为1千克浓缩铀的1/40.

1.1.4安全、无污染

核聚变不会产生长半衰期的放射性污染物，万一发生事故，反应堆会自动冷却而停止反应，不会发生爆炸.

图1　太阳的聚变反应示意图Figure 1　Fusion reaction schematic of the sun

1.2磁约束聚变

1.2.1约束方式

聚变原料发生聚变反应时，最佳温度高达一千万度.在这种高温下，电子被完全剥离出原子，形成物质第四态等离子体.当没有约束时，带电粒子的热运动会使等离子体迅速扩散，无法发生核聚变反应，所以需要外界约束使高温等离子体聚在一起，保持一定的密度，从而发生可观的核聚变反应.等离子体目前有两种约束方式，磁场约束和惯性约束.

1) 磁约束

磁场可以约束粒子，使其沿磁力线运动，如图2.等离子体作为带电粒子，会受到电磁场的影响，所以可以通过外加磁场约束等离子体.磁场是目前已知最好的绝缘体，其隔热性能比航天飞机的瓦片还要强1 000倍.

图2　磁场对粒子的约束Figure 2　Constraint of magnetic field on the particles

2) 磁约束中存在的问题

磁场只能约束粒子在垂直磁场方向的运动，但并不能约束粒子在平行磁场方向的运动，如图3，带电粒子在垂直磁场的方向做回旋运动，磁场不均匀性会产生梯度漂移.为此可以将磁场弯曲成环形，首尾相接，如图4，这样就可以把粒子约束在环中运动.

图3　带电粒子在磁场中的运动图Figure 3　Movement of charged particles in magnetic field

图4　环形磁场中螺旋形状磁场线的方向Figure 4　Direction of magnetic field lines with circular spiral shape in magnetic field

但是，当把磁场弯曲成环形时，磁场中存在垂直于磁场方向的梯度，粒子会发生垂直于磁场方向的梯度漂移.同时粒子沿着环形磁力线上的运动，会受到沿磁场曲率方向的离心力作用，从而产生一个垂直于离心力和外加磁场为方向的曲率漂移.因此需要再增加一个沿极向的磁场，使得粒子在不同位置处的漂移作用相互抵消，从而保证约束的稳定.

目前国际上比较主流的磁约束聚变装置有托卡马克和仿星器等，如图5(a).其中托卡马克由于其磁场设计的相对简单和约束性能的良好成为各国进行磁约束聚变研究的首选.仿星器有在稳态运行方面有其独特的优点，但是其复杂磁场的设计和建造也极有挑战性.

3) 惯性约束

除了磁约束的方法之外，还可以使用惯性来约束等离子体.宇宙中的许多星体都是依靠自身巨大质量产生的引力作用来约束粒子的，如图5(b)所示，上面为太阳依靠其巨大的惯性引力约束等离子体，下面为星云依靠其巨大的惯性引力约束等离子体.在实验室里可以通过强激光压缩氘氚靶丸实现惯性约束，如美国的国家点火装置(NIF)和我国的神光系列装置都是采用这一原理的.

图5　等离子体的约束Figure 5　Plasma confinement

1.2.2磁约束装置

1) 托卡马克(Tokamak)磁约束聚变实验装置

托卡马克是前苏联科学家发明的一种利用磁约束来实现磁约束聚变的环性容器，依靠环形线圈和等离子体电流产生的环状螺旋形强磁场，将极高温等离子体状态的聚变物质约束在环形容器里，以此实现聚变反应.

2) 国际磁约束核聚变实验装置

自从20世纪50年代以来，人类开始研究聚变能源及其密切相关的等离子体物理，测试了很多不同的实验装置，发现到目前为止托卡马克还是表现最好的.评判聚变装置约束效果的重要参数包括聚变等离子体的温度、密度以及约束时间，理论分析表明只有当这三者的乘积超过某一临界值时，燃料才能燃烧发生聚变，这就是著名的劳逊判据.自20世纪90年代以来，欧盟的JET、美国的TFTR、DIII-D和日本的JT-60、JT-60SA这几个大型托卡马克装置在磁约束核聚变研究中获得许多重要成果.图6为不同托卡马克试验装置大半径对比图.我们现在的实验装置越来越靠近劳逊判据的临界值，如图7和图8.另外，一个经验判定是，托卡马克尺寸越大越稳定，约束时间越长，越接近劳逊判据的临界值，这就是为什么现在托卡马克越做越大的原因.

图6　不同托卡马克试验装置大半径对比Figure 6　Major radius comparison among different Tokamak experiment devices

图7　不同托卡马克实验装置约束时间对比Figure 7　Confinement time comparison among different Tokamak experiment devices

图8　不同托卡马克实验装置约束效果对比Figure 8　Confinement effect comparison among different Tokamak experiment devices

随着研究进展的深入，各国之间的学术交流愈加频繁，国际热核聚变实验反应堆(International Thermonuclear Experimental Reactor，ITER)将成为世界上最大的磁约束等离子体物理实验装置，如图9. 这是目前正在建设的世界上最大的实验性托卡马克核聚变反应堆，由七个成员实体资助和运行，包括欧盟、印度、日本、中国、俄罗斯、韩国和美国.它建立在TFTR、欧洲联合环形加速器(JET)、JT-60和T-15等装置的研究之上，并将显著的超越所有前者.ITER实验成功后将是人类历史上第一个长时间实现核聚变反应的实验装置，对整个聚变能源科学的影响是巨大的.

国际热核反应试验堆计划(ITER)是商用化核聚变能源的关键一步.作为ITER成员，中国在国家中长期科技规划中把ITER计划作为重点高技术，投入近百亿人民币进行研究.我国关于ITER采购包的研制在我国科研和工程技术人员的协同努力下进展顺利，在七方成员中排在前列，体现了我国的科学技术实力和综合国力.

图9　国际热核反应试验堆(ITER)结构示意图Figure 9　Structure of ITER

ITER计划中的等离子体的参数：

·等离子体大半径：6.2 m

·等离子体小半径：2.0 m

·等离子体容量：840 m3

·等离子体电流：15.0 MA

·轴向环形磁场强度：5.3T

·聚变功率：500 MW

·等离子体维持时间：>400s

·能量倍增因数(Q值)：>10

(3) 国内磁约束核聚变实验装置

目前，国内主要的托卡马克实验装置有中科院等离子体所的EAST(图10)和核工业部西南物理研究院的HL-2A(图11).

图10　中科院等离子体所EAST超导托卡马克Figure 10　EAST superconducting tokamak in Institute of Plasma Physics, Chinese Academy of Sciences

图11　核工业部西南物理研究院HL-2A托卡马克Figure 11　HL-2A tokamak in Southwestern Institute of Physics, Department of Nuclear Industry

先进实验超导托卡马克实验装置(Experimental Advanced Superconducting Tokamak，EAST)是一个具有非圆小截面的全超导托卡马克.它可以实现高参数和长脉冲的实验运行；科研人员在以上条件下可以开发先进运行模式，并进行热流平衡和粒子流平衡控制的实验研究.

环流器二号A(HL-2A)是我国第一个具有先进偏滤器位形的非圆截面的托卡马克核聚变实验研究装置，可以进行高参数等离子体条件下的改善约束实验，并利用其独特的大体积封闭偏滤器结构，开展核聚变领域许多前沿物理课题以及相关工程技术的研究.

1.3磁约束聚变的目标和难点

磁约束聚变的目标是使粒子在扩散之前发生聚变，并让聚变产生的alpha粒子加热燃料，从而实现自持燃烧.实现这些目标需要对磁约束聚变发生的等离子体物理有深刻的理解，主要涉及等离子体的约束、输运、加热和电流控制等复杂物理过程.同时这些聚变等离子体物理需要研究波-粒子、波-波以及粒子-粒子等多时空尺度下复杂的非线性行为，需要设计复杂的计算机模拟来辅助装置设计，物理实验设计以及实验解释和预测.从20世纪90年代开始，磁约束聚变等离子体模拟就开始使用日益兴起的超级计算技术进行大规模并行模拟，开发了针对聚变等离子体宏观微观不稳定性、湍流输运和加热物理研究的大规模数值模拟程序，并兴起了以回旋动理学模拟为主导的模拟科学.

2大规模并行数值模拟

2.1大规模并行数值模拟的起源

大规模并行数值模拟是指将一个复杂的计算问题分成若干部分，通过以网络(光纤)相互联接的大量的计算机核(几百到20万核)的超级计算机，同时计算同一个任务的不同部分.其目的是提高问题求解速度，同时扩大求解问题规模.

大规模并行数值模结合了最尖端的计算机科学、应用数学和具体科技应用领域的跨学科全新研究方法，适应于那些对科学研究和技术创新有重大革新性意义的课题，适合于团队作业.

2.2大规模并行数值模拟的发展

数值模拟已经成为除理论、实验外，支持科学探索和技术革新的第三个主要研究手段.大规模数值模拟能够帮助理解和预测那些科学技术上极其重要的系统的行为，从而加速科技创新的速度.超级计算能力已成为衡量一个国家(地区)科技实力和创新能力的重要标志.

2.3超级计算机的世界分布

大规模数值模拟从20世纪90年代中叶开始兴起，最早的超级计算机计算能力约为1G flops，其计算能力以每年2～3倍的速度增加.现在世界上最强的超级算计机的速度在1015flop量级，正在向1018flop进军.目前世界上最强的超级算计主要集中在美国、中国、欧洲和日本.其中美国的超级计算资源占到全世界一半左右.

1) 国际超级计算机

近几年，世界上排名前500的超级计算机中，较著名的有美国橡树岭国家实验室的“泰坦”，美国劳伦斯利福摩尔国家实验室的“红杉”，日本理化学研究所的“京”，美国阿贡国家实验室的“米拉”等.

2) 国内超级计算机

中国硬件发展上已经成为仅次于美国的超级计算大国，深圳星云超级计算机，曾排名世界第二；天津天河超级计算机，2011排名世界第一；广州天河-2超级计算机，2014排名世界第一.

现阶段我国超级计算机发展中的主要问题是软件发展和硬件发展不相称.超级计算平台辅助软件和大规模数值模拟应用程序的发展严重滞后于超级计算机的建造.

2.4大规模数值模拟的应用

大规模数值模拟广泛应用于新能源、新材料、物理、化工、生物、气候环境、物流、金融等领域，对国民经济和科技创新产生广泛而深刻的影响，如图12.

图12　大规模数值模拟应用举例Figure 12　Application example of large-scale numerical simulation

3回旋动理学模拟

基于磁约束聚变等离子物理的高度复杂性和多时空尺度特性，回旋动理学模拟已成为研究聚变中不稳定性和湍流输运的主要工具.近几十年来的研究表明，托卡马克中普遍存在的电磁场微扰是造成托卡马克反常输运的主要原因，一般也称之为湍流输运.这些电磁场微扰是由各种宏观和微观的电磁不稳定性激发的.聚变等离子体约束的好坏直接决定于其输运过程，其产生和控制的物理机制是目前研究的前沿课题.

3.1等离子体的输运过程

3.1.1输运过程的种类

在等离子体中，输运过程可以分为碰撞输运与湍流输运.

1) 碰撞输运

等离子体中粒子之间会存在相互作用，一般称为碰撞，可以用碰撞算符来表示.碰撞可以使粒子回旋运动的导心或者沿着磁力线运动的香蕉轨道中心产生偏移，从而导致碰撞输运，如图13.碰撞输运即使在没有电磁场扰动的情况下仍然存在，是托卡马克装置最低水平的输运过程.

图13　带有相反电荷的粒子由于导心漂移发生碰撞Figure 13　collision of particles with opposite charge due to guide heart drift

2) 湍流输运

湍流是托卡马克中粒子和热输运的主要原因.湍流输运可以分为两种，静电性和电磁性.根据其不稳定性来源又可细分为各种不同模，比如离子梯度模(ITG)、电子梯度模(ETG)、捕获电子模(TEM)、动理学气球模(KBM)，等等.每个模线性不稳定性原因不一样，同时饱和机制和输运机制也往往不一用，从而导致输运系数不一样.一种最常见湍流输运原因就是带电粒子的在静电场微扰下的EXB漂移，这种垂直于磁场的漂移由于电场的退相关过程而导致随机运动，从而导致径向的湍流输运，如图14.

图14　导心的EXB漂移导致湍流输运Figure 14　Turbulent transport because of EXB drift of guide heart

3.2回旋动理学简介

3.2.1Vlasov方程与Maxwell方程

等离子体有动理学和流体力学两种描述方式，其中流体力学描述可通过对动理学方程求矩获得，但是它忽略了朗道阻尼等重要动理学内容，因而不能准确描述聚变等离子体中一些重要的动理学不稳定性及其湍流输运.最一般的动理学方程可以从非平衡态统计力学中的BBGKY递推关系获得如下的带电磁场的玻尔兹曼方程

(1)

-▽2φ=4π(qi∫d3vfi-e∫d3vfe).

(2)

其中，f表示单粒子的相空间分布函数.第一个方程在等离子体物理被称之为含碰撞的Vlasov方程，方程右边为代表两粒子相关函数的碰撞算符.为简单起见，我们用第二个方程即泊松方程代替求解电磁场的Maxwell(麦克斯韦)方程组.这组方程可以视为静电极限下的Vlasov-Maxwell方程组.上面这组方程可以描述时间尺度从等离子体震荡到输运，空间尺度从德拜长度到系统尺寸等大范围多尺度物理.依靠现在的超级计算机的计算能力是不可能模拟这么大范围的多尺度物理.

但在托卡马克中引起湍流输运最危险的模是低频漂移波湍流，比如ITG、TEM、KBM和ETG等，在燃烧等离子体中可能会激发比较高频的Alfven波，但是仍然低于离子回旋频率，如图15.

图15　托卡马克中不稳定性的时空频率特点Figure 15　Space and time frequency characteristics of instability in Tokamak

(3)

在这种条件下，我们可以将式(3)的Vlasov方程进行坐标变换：

(x,v)→(R,μ,v||),

(4)

将方程从粒子坐标移到导心坐标，然后再回旋平均得到如下的回旋动理学(gyrokinetics)-麦克斯韦方程组[1-6]：

=C[f].

(5)

相应的回旋动理学泊松方程整理如下：

(6)

其中

代表从导心到粒子位置的反演[7].强磁场下的导心运动如图16.

图16　强磁场下的导心运动Figure 16　Movement of guide heart in strong magnetic field

3.3回旋动理学模拟

3.3.1模拟方法和算法特点

回旋动理学模拟是研究磁约束等离子体微观不稳定性中非线性物理的重要工具.它将六维相空间的动理学方程变成五维相空间，大大提高计算效率.相对流体模拟而言，它又保留了磁约束聚变等离子体物理中如朗道阻尼重要的动理学效应，可以比较真实地描述等离子体物理.等离子体物理模拟一般通过将模拟结果与理论分析进行对比来验证程序真实反映了理论模型，再用模拟与实验结果进行比较来验证物理模型的可信度，最终达到模拟的可预测性.

回旋动理学湍流模拟的理论基础起源于20世纪70年代，从90年代以来随着超级计算机和大规模数值模拟的发展而获得蓬勃发展.回旋动理学-麦克斯韦方程体系有两种主要数值方法可求解其动力学行为，一种叫粒子模拟方法，即用蒙特卡洛的方法对相空间取样；另外一种是用解多维偏微分方程的网格法，也叫Vlasov方法或者连续法.在算法上，为了去除模拟中的粒子数或网格数与物理要求相差很远而导致的噪声，我们一般采用所谓部分分布函数法，关注分布函数中偏离平衡分布的部分，从而提高信噪比.

3.3.2模拟程序

从20世纪90年代以来，涌现了很多回旋动理学程序.这些程序的发展代表了磁约束聚变模拟这二十年来最富代表性的发展历程.代表性的程序美国有GTC、GYRO、GS2、GEM、XGC等，欧洲有GENE、ORB5等，日本有GT3D等.

其中，GTC(Gyrokinetic Toroidal Code)程序[8]是美国加州大学的林志宏教授90年代从普林斯顿读研究生时开始发展的三维全域性粒子回旋动理学程序.历经二十年的发展，已成长为一个包含了微观湍流、动理学磁流体、射频加热等多功能的模拟程序或者模拟平台.近年来浙江大学、中科院物理所和北京大学也积极参与了其程序开发.

GTC程序的创新之一体现在其采用磁坐标，构造了沿着磁力线的三维电磁场网格，如图17，图18和图19.在某一个极面上GTC采用非结构化网格，保证径向和极向计算精度大致相近；在同一个磁面上，格点沿着磁力线成为一条直线.沿着磁力线的格点设置契合磁约束聚变等离子体各项异性的特点.回旋平均和导心到粒子位置的反演都采用了所谓4点平均的办法[9].这些计算算法的创新使得GTC能够进行真正三维的实空间的全域模拟，同时大大提高了计算效率.

图17　GTC磁面上的格点设置Figure 17　Lattice point set on magnetic surface of GTC

图18　GTC极面上的格点设置Figure 18　Lattice point set on polar surface of GTC

图19　GTC的3维格点设置和湍流特点Figure 19　3D point set and turbulence characteristics of GTC

3.3.3粒子推动方程

回旋动理学粒子模拟方法主要由两部分组成，导心(或者回旋中心)运动积分器和电磁场解法器.导心的运动方程可以描述如下：

(7)

(8)

假设磁场扰动可以写成如下形式：

δB=▽×αB,

(9)

ρc=ρ||+α,

(10)

D=ρc(gI′-Ig′)+I+qg,

(11)

磁坐标下的运动方程可以表述为[10]：

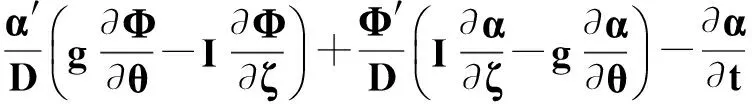
(12)

(13)

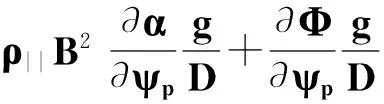
(14)

(15)

式(12)～(15)这组导心运动方程可以用来描述导心在托卡马克中运动，一般用2阶龙格库塔方法来积分导心轨道，因为它是一种显式算法，可以和描述碰撞的蒙特卡洛方法相匹配.

3.3.4泊松方程

(16)

式(16)的关键在于计算分子中的拉普拉斯算符(Laplacian).

3.3.5一般几何位型下的拉普拉斯算符

磁坐标下的拉普拉斯算符(Laplacian)展开可得

(17)

其中，协变张量gxy可以通过B样条方法计算得出.逆变张量gxy可以通过协变张量gxy计算得出.

3.4基于回旋动理学模拟的发现

回旋动理学模拟能够帮助解释实验现象和促进理论的发展，并为实验建模提供必需的参数.

3.4.1带状流对湍流的抑制

回旋动理学模拟最有影响的结果之一是模拟发现湍流会自发激发带状流(zonal flow)，从而反过来抑制湍流[7]，如图20.这一模拟上的发现极大促进人们对于湍流理论和实验的理解，比如促进了漂移波参量不稳定性理论的发展[11].我国的实验也多次发现了带状流对湍流的调制作用[12-13].

3.4.2湍流输运系数

关于磁约束聚变等离子体输运过程的集成建模迫切需要在给定等离子体径向剖面的条件下湍流输运的强度，基于第一性原理的回旋动理学模拟能够提供湍流输运的系数[15]，如图21.而对于湍流强度的径向分布目前很难用现有理论预测.

图20　GTC模拟发现捕获电子模湍流中带状流对湍流有抑制作用[14]Figure 20　GTC simulation found that capture banded in electronic mode turbulence flow has inhibitory effect on turbulence

图21　回旋动理学模拟提供的热传导系数的径向分布Figure 21　Radial distribution of heat transport coefficient by gyrokinetic simulation

4结语

本文介绍了磁约束核聚变中的基于回旋动理学的大规模数值模拟.最近20年来这个领域已经取得很大进步，但是还有很多关键性问题没有得到解决，比如聚变等离子体边界电磁模拟和长时间尺度模拟，仍需要研究人员的持续努力.同时，这个领域随着超级计算技术的进步，将会进一步促进可控磁约束聚变的实现.

(致谢：本文作者感谢袁泉准备部分初稿并仔细校对文稿，同时感谢P.J. Catto和Z. Lin博士提供部分插图.)

【参考文献】

[1]CATTO P J. Linear gyrokinetics[J]. Plasma Physics,1978,20:719.

[2]ANTONSEN T, LANE B. Kinetic equations for low frequency instabilites in inhomogeneous plasmas[J].Physics of Fluids,1980,23(6):061205.

[3]FRIEMAN E A, CHEN L. Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria[J]. Physics of Fluidsvol,1982,25(3):502-508.

[4]HAHM T S. Nonlinear gyrokinetic equations for tokamak microturbulence[J]. Physics of Fluids,1988,31(9):2670-2673.

[5]QIN H W, TANG M, REWOLDT G. Gyrokinetic theory for arbitrary wavelength electromagnetic modes in tokamaks[J]. Physics of Plasmas,1998,5(4):1035-1049.

[6]LEE W W. Nonlinear gyrokinetic equations[J]. Physics of Fluids,1983,26(12):3524.

[7]LIN Zhihong, HAHM T S, LEE W W, et al.Turbulent transport reduction by zonal flows: Massively parallel simulations[J]. Science,1998,281(5384):1835-1837.

[8]LEE W W. Gyrokinetic particle simulation model[J]. Journal of Computational Physics,1987,72(1):243-269.

[9]LIN Z, LEE W W. Method for solving the gyrokinetic Poisson equation in general geometry[J]. Phys Rev E,1995,52(5):5646-5652.

[10]WHITE R B, CHANCE M S. Hamiltonian guiding center drift orbit calculation for plasmas of arbitrary cross-section[J]. Physics of Fluids,1984,27(10):2455-2467.

[11]CHEN L, LIN Z, WHITE R B. Excitation of zonal flow by drift waves in toroidal plasmas[J].Physics of Plasmas,2000,7(8):3129.

[12]ZHAO K J, LAN T, DONG J Q, et al. Toroidal symmetry of the geodesic acoustic mode zonal flow in a tokamak plasma[J]. Physical Review Letters,2006,96(25):255004.

[13]XU G, WAN B N, SONG M, et al. Direct measurement of poloidal long-wavelength E× B flows in the HT-7 tokamak[J]. Physical Review Letters,2003,91(12):125001.

[14]XIAO Y, LIN Z. Turbulent transport of trapped-electron modes in collisionless plasmas[J]. Physical Review Letters, 2009,103(8):085004.

[15]XIAO Y, HOLOD I, WANG Z X, et al. Gyrokinetic particle simulation of microturbulence for general magnetic geometry and experimental profiles[J]. Physics of Plasmas,2015(22):022516.

Massively parallel gyrokinetic simulation for magnetic fusion plasmas

XIAO Yong

(Institute for Fusion Theory and Simulation, Zhejiang University, Hangzhou 310027, China)

Abstract:This article introduces the magnetic fusion energy science and its associated fusion plasma physics. Massively parallel gyrokinetic simulation has emerged as a major tool to study the nonlinear physics. Its research frontier is also discussed.

Key words:plasma; fusion; magnetic confinement; large scale data simulation; gyrokinetics

【文章编号】1004-1540(2016)01-0001-10

DOI:10.3969/j.issn.1004-1540.2016.01.001

【收稿日期】2016-01-18《中国计量学院学报》网址：zgjl.cbpt.cnki.net

【作者简介】肖湧(1977- )，男，湘南省湘潭人，教授，主要研究方向为磁约束核聚变等离子体中的不稳定性，输运和加热以及大规模并行回旋动理学模拟等. E-mail:yxiao@zju.edu.cn

【中图分类号】O532+.11

【文献标志码】A