一种新的鲁棒主成分分析方法及其应用

陈甲英，赵建伟，曹飞龙

(中国计量学院 理学院，浙江 杭州 310018)



一种新的鲁棒主成分分析方法及其应用

陈甲英，赵建伟，曹飞龙

(中国计量学院 理学院，浙江 杭州 310018)

【摘要】背景建模在视频运动分析中具有重要作用.视频序列背景图像通常具有低秩性，为了更好地刻画该特性，精确提取视频背景，提出了一种基于截断核范数的鲁棒主成分分析模型.同时设计了一种两步迭代算法来求解该模型，最后将该算法应用于视频背景建模.不同视频数据库实验表明，该算法对于求解背景建模问题是有效的.

【关键词】矩阵恢复；截断核范数；鲁棒主成分分析；背景建模

如何较准确地从视频流中提取运动目标是计算机视觉研究领域中的一个重要的方向.同时，也是行为理解和运动分析的重要前提.在实际应用中，常见的运动目标检测算法主要有三类：光流法[1]，相邻帧间图像差分法[2]以及背景图像差分法[3].相比于前两种方法，背景图像差分法更加精确、速度更快并且实现比较简单，是目标检测中一种常用的方法.其基本原理如下：首先估计背景图像，然后利用背景图像与当前帧图像的差进行目标检测.因此，背景图像建模是背景图像差分法进行目标检测的关键.

根据摄像机拍摄方法的不同，视频可以被分为摄像机固定拍摄的定视角视频和摄像机运动拍摄的变视角视频两类，本文主要针对前者进行背景建模问题研究.国内外对于这一问题已有很多学者进行了研究，提出了一些不同的建模方法.如：Wren等人[4]提出的单高斯分布模型，在单高斯模型的基础之上Friedman和Russell[5]提出了混合高斯背景模型.而混合高斯分布模型的缺点是参数估计较慢，模型个数难以确定.为了从根本上解决混合高斯背景模型中参数估计运算量过大的问题，编码本(Codebook)背景建模方法[6-7]及非参数背景建模[8]被提出.从本质上看，由于这些方法全部是建立在对像素点的分析上，算法虽然实现简便，但是忽视了像素点间的联系和物体的整体属性，在一些视频中，仅通过像素值出现的频率和稳定性并不能准确区分前景和背景.例如，体积较大的单色物体在运动过程中，其内部经常会判定为稳定的背景.近年来，随着压缩感知理论研究的深入，稀疏表示成为一种更加有效的数据表示方式.然而，现实世界中很多数据是以矩阵形式存储的，因此，将向量样例的稀疏表示推广到矩阵的低秩情形的低秩矩阵恢复理论应运而生.考虑到视频序列各帧之间的相关性，Candès等人[9]用矩阵恢复方法来提取摄像机固定的情况下的视频图像的背景，并且得到了理想的提取效果.已有的矩阵恢复方法虽然考虑了每帧图像像素之间的联系，但是核范数可能不是刻画各帧图像之间的低秩性的最好方法.因此，寻找一种更好的矩阵恢复方法并用其进行背景提取无疑是具有重要的理论和现实意义.

本文结构如下：第一节简单介绍基于核范数的鲁棒主成分分析方法；第二节提出一种新的基于截断核范数的鲁棒主成分分析算法并给出了相应的求解方法；第三节是实验部分，包括人工数据有效性实验和背景提取两个实验；第四节是结论.

1基于核范数的鲁棒主成分分析方法

在固定摄像机位置的情况下，可得到一段时间内的一个视频序列.由于摄像机是静止的，所以只要没有运动物体经过，视频背景是固定的.也就是说，在一段视频图像中，可将运动物体看作背景部分的噪声项，除去噪声项，各帧图像的背景部分是线性相关的，即一段视频中，所有背景图像构成的矩阵是低秩的，运动的前景可以看作是稀疏的噪声.

考虑一个视频序列中的N帧图像，分别记为{I1,I2,…,IN}，其中Ii(i=1,2,…,N)是一个m×n的图像矩阵.将每个图像矩阵Ii拉成列向量，按照原来视频序列中各帧图像的顺序重新生成一个mn×N的矩阵D.对于矩阵D，可以分解成运动目标E和固定背景Z的和，即D=Z+E.根据前面的分析，各帧图像的背景拉成的向量是线性相关的，即矩阵Z具有低秩性，而运动目标在图像中可以看作噪声，具有一定的稀疏性.因此，背景建模问题事实上就是求解以下低秩矩阵恢复问题：

s.tD=Z+E.

(1)

然而，由于秩函数以及零范数的非凸性，该模型是一个NP难问题[10-11].Fazel[12]首次在控制系统中用核范数作为秩函数的近似，之后大量理论研究说明：在满足强不相干性条件[9,13]和约束等距条件[14]的前提下，核范数可以作为秩函数的一种凸替代；同时，l1范数可以作为l0范数的凸替代[10,13].在文献[9]和[14]中，Candès等人提出了一种主成分追踪方法:

s.tD=Z+E.

(2)

我们将这种基于核范数的背景提取方法又称为基于核范数的鲁棒主成分分析方法(Robust Principal Component Analysis Method with Nuclear Norm，RPCA-NN).此外，一些研究者还考虑了有噪声存在的情况下的低秩矩阵恢复问题[15-16]，并给出了相关算法.

事实上，模型(2)可以用迭代阈值方法求解(Iterative Threshold，IT)[15,17]来求解，但是，IT迭代步长不好选择，而且需要迭代很多次才能收敛.为了克服IT收敛速度慢的局限性，Lin等人[18]提出了两种新的求解该问题的方法，分别是加速近端梯度算法(Accelerated Proximal Gradient，APG)和对偶算法(Dual Method，DM).此外，文献[19]提出了增广拉格朗日算法(Augmented Lagrange Multiplier，ALM)和非精确增广拉格朗日算法(Inexact Augmented Lagrange Multiplier, IALM)来求解(2)式，使得其迭代解能够收敛到该优化问题的精确解，并且耗时相对较少.

2基于截断核范数的鲁棒主成分分析方法

由于在提取背景时，人们期望背景部分是低秩的，Hu等人指出核范数不是秩函数的最佳近似，因为原始的秩函数只需要考虑非零奇异值的个数，且每个非零奇异值对秩函数有着同等的贡献，而核范数是所有非零奇异值的和，但不同的非零奇异值对核范数的影响不同，大的奇异值起了主要的作用.对于一个矩阵D∈Rm×n，它的秩在很大程度上是取决于最小的min(m,n)-r个奇异值的非零元素的个数，前r个奇异值在估计秩时提供的信息是非常有限的，而核范数中起决定作用的恰恰是前面的较大的奇异值.基于此Hu等人[20]提出了一种更精确的低秩性的刻画方式，即截断核范数正则化方法(Truncated Nuclear Norm，TNN).

首先，介绍截断核范数的概念：

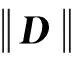
其中σi(D)是D的第i个奇异值，r为整数，且r小于矩阵的秩rank(D).

受Hu等人研究的启发，本文提出了一种基于截断核范数的鲁棒主成分分析方法(Robust Principal Component Analysis Method with Nuclear Norm，RPCA-TNN):

s.tD=Z+E.

(3)

然而，由于截断核范数是非凸的，因此模型(3)是一个NP-Hard问题[10-11]，无法用凸优化的方法来求解该模型.然而，截断核范数具有以下性质[20]:

引理1[20]对于任意的矩阵Z∈Rm×n，任意的非负整数r(r≤min(m,n))，存在秩为r的矩阵A∈Rr×m和B∈Rr×n，且有AAΤ=I，BBΤ=I，有如下的结论：

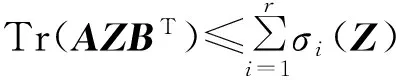
(4)

其中σi(Z)是Z的第i个奇异值.

该引理的证明已在文献[20]中给出.

根据引理1和奇异值分解的知识，我们可以得到下面的结论：

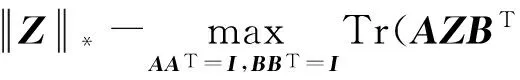
(5)

因此，在A和B确定的情况下，根据(5)式，上述优化问题(3)可以转化为求解下面的优化问题：

s.tD=Z+E.

(6)

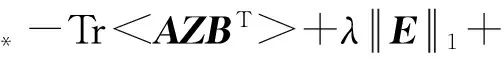
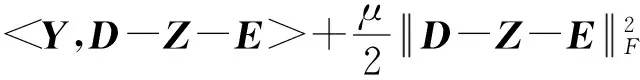
(7)

其中Y是拉格朗日乘子，μ>0是惩罚参数，<.,.>为矩阵内积.

通过交替方向法求解下面的无约束优化问题：

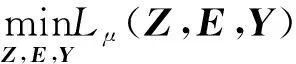
即固定其中两个变量，求解剩下的一个变量：

(8)

为了求解上面的问题，给出以下定义和引理：

定义2[21-22]矩阵D∈Rm×n的奇异值分解为：

D=USVT,S=diag({σi}1≤i≤min(m,n))，定义奇异值阈值算子：

Θτ(D)=UΘτ(Σ)VT,

其中σi是D的第i个奇异值.

引理2[21-22]对于τ>0，Y∈Rm×n，下面的结论成立：

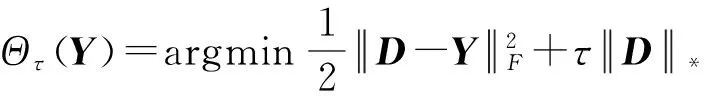
引理3[9,23]对于τ>0，Y∈Rm×n设Sτ:R→R是软阈值算子，则它是下面优化问题的解：

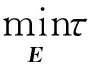
且软阈值算子

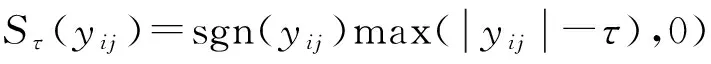
其中Y=(yij).

我们首先固定E和Y，更新Z,即求解下面的优化模型：

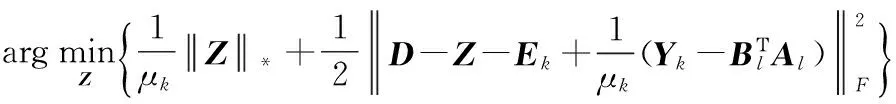
从而根据引理2和定义2，可以得到Z的解为下面的形式：

(9)

然后，我们固定Z和Y，更新E：

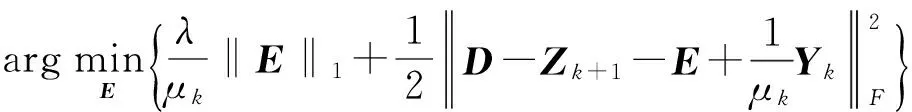
再根据引理3得到E的迭代解如下：

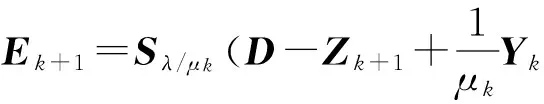
(10)

最后，计算拉格朗日乘子Y和惩罚参数μ：

Yk+1=Yk+μk(D-Zk+1-Ek+1),

(11)

μk+1=min(ρμk,μmax),

(12)

其中ρ>1是一个常数.

应用两步迭代策略交替迭代直到算法收敛.算法总结如下.

两步迭代算法：

步骤一，初始化

1)给定初值Z1=D；

2)给定第二步迭代收敛误差eps；

3)给定终止误差ε.

步骤二，计算Al和Bl

计算Zl的奇异值分解

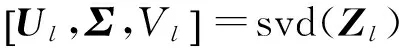
其中，

Ul=(u1,u2,…,um)∈Rm×m,

Vl=(v1,v2,…,vn)∈Rn×n，

从而，Al=(u1,u2,…,ur)Τ，

Bl=(v1,v2,…,vr)Τ.

步骤三，用交替方向法求解优化子问题(6)

1)用(9)式更新变量Z；

2)用(10)式更新变量E；

3)用(11)式更新拉格朗日乘子Y.

4)用(12)式更新惩罚参数μ.

直到算法收敛,即

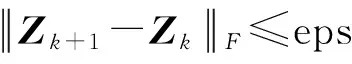
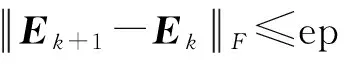
步骤四，转到步骤二重复迭代循环，更新变量，直到外部算法收敛，即

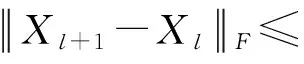
3实验结果及分析

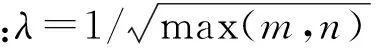
3.1人工数据实验

根据文献[24]，人工数据矩阵按如下方式生成：首先生成一个秩为r的低秩方阵Z0∈Rm×n和一个相同大小的稀疏矩阵E0，则待恢复的矩阵D0可以表示为D0=Z0+E0.

为说明提出的基于截断核范数的鲁棒主成分分析方法要优于基于核范数的鲁棒主成分分析方法,本文用RPCA-TNN和RPCA-NN分别提取人工数据D0的低秩部分Z，并用Z的秩、低秩误差以及总体误差来刻画两种方法的有效性，其中低秩误差和总体误差的定义形式如下[24]：

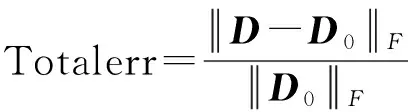
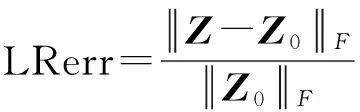
本文用到的矩阵大小分别是200、600、1 000、1 300的人工数据方阵来做实验，从表1可以发现：不论是RPCA-TNN,还是RPCA-NN都能够很好地提取人工数据矩阵的低秩部分.但是，RPCA-TNN不论是总误差还是低秩误差都要比

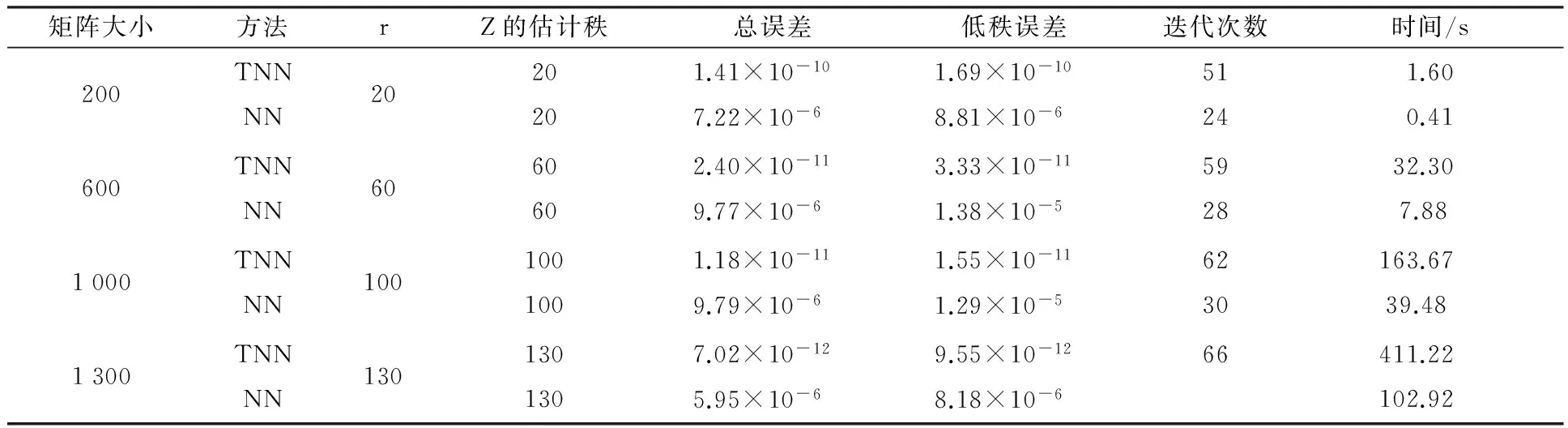
表1　RPCA-TNN和RPCA-NN在人工数据上的实验结果

图1　利用RPCA-TNN和RPCA-NN来提取背景并检测单一前景Figure 1　Background subtraction and simple foreground object detection by RPCA-TNN and RPCA_NN

RPCA-NN小至少三个数量级.这说明较之RPCA-NN，RPCA-TNN能够更好地处理低秩提取相关的问题.此外，从表1看出，RPCA-TNN耗时更多一些，但是，这是可以理解的：奇异值分解是比较耗时的运算.

3.2背景提取与前景检测

本小节中，我们用七个由静态摄像机拍摄的监控视频数据做实验，即：Labby dataset，Escalator dataset，Fountain dataset，Campus dataset，Water Surface dataset，Hall dataset和Bootstrap dataset[25].分别用RPCA-TNN和RPCA-NN提取以上视频数据的背景，并且将提取的结果进行直观的比较，实验结果显示在图1和图2中.由于实验条件的限制，在每个视频数据集上，我们分别取35帧视频图像做实验.由于所有的视频图像都是彩色的，首先需要将视频图像转成灰度图像，然后将每一帧灰度图像拉成一个长列向量，最后将这35个列向量并成矩阵D.

图2　利用RPCA-TNN和RPCA-NN来提取背景并检测复杂前景Figure 2　Background subtraction and complex foreground object detection by RPCA-TNN and RPCA-NN

图1和图2呈现了用RPCA-TNN和RPCA-NN在每个视频数据集上的背景提取结果.其中前三列是用本文提出的方法得到的结果，第一列是含有噪声或运动物体的视频图像，第二列是提取背景后剩余的运动物体或噪声，第三列是利用本文提出的方法提取的背景部分.同样的，后三列是用RPCA-NN得到的提取结果.

从图1直观观察，我们发现当视频帧数比较少，视频场景中的运动物体比较单一的情况下，RPCA-TNN和RPCA-NN都能够提取出视频的背景图像.但是，与RPCA-TNN相比，我们很容易发现：用RPCA-NN提取出的运动前景物体中还包含了很少的一部分背景，也就是说提取的背景图像有损失.所以，在处理背景建模问题时，本文提出的RPCA-TNN方法的提取效果要优于一般的RPCA-NN.

图2中的视频场景比较复杂，含有多运动物体.我们发现当视频帧数很少时，RPCA-NN已经不能够提取出视频的背景模型了，而本文提出的RPAC-TNN仍然能够比较精确的提取出视频背景.

4结语

本文提出了一种基于截断核范数的鲁棒主成分分析算法，使其能够更好地恢复低秩稀疏矩阵.由于截断核范数的非凸性，我们设计了两步迭代算法，并将该算法应用于背景建模中.实验结果表明，本文提出的方法相比一般的基于核范数的方法能更好地处理背景建模问题.

【参考文献】

[1]WEI hiqiang, JI Xiaopeng, WANG Peng. Real-time moving object detection for video monitoring systems [J]. Journal of Systems Engineering and Electronics,2006,17(4):731-736.

[2]LIPTON A J, FUJIYOSHI H, PATIL R S. Moving target classification and tracking from real-time video [C]// Proceedings of 4th IEEE Workshop on Applications of Computer Vision. New Jersey: IEEE, 1998: 8-14.

[3]CHEN Baisheng, LEI Yunqi, LI Wangwei. A novel background model for real-time vehicle detection [C]// Proceedings of 7th International Conference on Signal Processing. Beijing: IEEE, 2004, 2: 1276-1279.

[4]WREN C R, AZARBAYEJAIN A, DARRELL T. Pfinder: real-time tracking of the human body [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7): 780-785.

[5]FRIEDMAN N, RUSSELL S. Image segmentation in video sequences: a probabilistic approach [C]// Proceedings of 13th Conference on Uncertainty in Artificial Intelligence (UAI). San Francisco: Morgan Kaufmann Publishers Inc,1997：175-181.

[6]KIM K, CHALIDABHONGSE T H, HARWOOD D, et al. Real-time foreground-background segmentation using Codebook Model [J]. Real-Time Imaging, 2005, 11(3): 172-185.

[7]ILYAS A, SCUTURICI M, MIGUET S. Real time foreground-background segmentation using a modified Codebook Model [C]// Proceedings of 6th IEEE International Conference on Advanced Video and Signal Based Surveillance. Genova: IEEE, 2009: 454-459.

[8]ELGAMMAL A, DURAISWAMI R, HARWOOD D, et al. Background and foreground modeling using nonparametric kernel density estimation for visual surveillance [J]. Proceedings of the IEEE, 2002, 90(7): 1151-1163.

[10]NATARAJAN B K. Sparse approximate solutions to linear systems [J]. SIAM Journal on Computing, 1995, 24(2): 227-234.

[11]RECHT B, FAZEL M, PARRILO P A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization [J]. SIAM Review, 2010, 52(3): 471-501.

[12]FAZEL M. Matrix rank minimization with applications [D]. Stanford: Stanford University, 2002.

[15]GANESH A, WRIGHT J, LI Xiaodong, et al. Dense error correction for low-rank matrices via principal component pursuit [C]// Proceedings of 2010 IEEE International Symposium on Information Theory (ISIT). Austin: IEEE, 2010: 1513-1517.

[16]ZHOU Zihan, LI Xiaodong, WRIGHT J, et al. Stable principal component pursuit [C]// Proceedings of 2010 IEEE International Symposium on Information Theory (ISIT). Austin: IEEE, 2010: 1518-1522.

[17]WRIGHT J, GANESH A, RAO S, et al. Robust principal component analysis: exact recovery of corrupted low-rank matrices via convex optimization [C]// Advances in Neural Information Processing Systems. Granada: NIPS, 2009: 2080-2088.

[18]LIN Zhouchen, GANESH A, WRIGHT J, et al. Fast convex optimization algorithms for exact recovery of a corrupted low-rank matrix [J]. International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), 2009, 61: 213-216.

[19]LIN Zouchen, LIU Risheng, SU Zhixun. Linearized alternating direction method with adaptive penalty for low-rank representation [C]// Advances in Neural Information Processing Systems. Granada: NIPS, 2011: 612-620.

[20]HU Yao, ZHANG Debing, YE Jieping, et al. Fast and accurate matrix completion via truncated nuclear norm regularization [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(9):2117-2130.

[22]LIU Yuanyuan, JIAO Licheng, SHANG Fanhua, et al. An efficient matrix bi-factorization alternative optimization method for low-rank matrix recovery and completion [J]. Neural Networks, 2013, 48: 8-18.

[23]COMBETTES P L, WAJS V R. Signal recovery by proximal forward-backward splitting [J]. Multiscale Modeling & Simulation, 2005, 4(4): 1168-1200.

[24]YUAN Xxiaoming, YANG Junfeng. Sparse and low-rank matrix decomposition via alternating direction methods [J]. Operations Research & Management Science, 2013, 9(1): 167-180.

[25]Statistical modeling of complex background for foregrou-nd object detection [DB]. http://perception.i2r.a-star.edu.sg/bk_model/bk_index.html[2015-09-28].

A novel robust principal component analysis method and its applications

CHEN Jiaying, ZHAO Jianwei, CAO Feilong

(College of Sciences, China Jiliang University, Hangzhou 310018, China)

Abstract:Background modeling is critical in the video motion analysis. To describe the low rank property of a set of video sequences and to improve the accuracy of background modeling, a novel robust principal component analysis with the truncated nuclear norm method was proposed. A model with a two step iterative strategy was used to solve the problem. Finally, the algorithm was applied in the video background modeling. A series of experiments on different video databases demonstrated that the algorithm was effective for the solving of the background modeling problem.

Key words:matrix recovery; truncated nuclear norm; robust principal component analysis; background modeling

【文章编号】1004-1540(2015)01-0113-08

DOI:10.3969/j.issn.1004-1540.2016.01.021

【收稿日期】2015-10-06《中国计量学院学报》网址：http://zgjl.cbpt.cnki.net

【基金项目】国家自然科学基金资助项目(No.61571410,61272023).

【作者简介】陈甲英(1990- )，女，甘肃省金昌人，硕士研究生，主要研究方向为矩阵恢复.E-mail:zccyman@163.com

【中图分类号】TP399

【文献标志码】A

通信联系人：曹飞龙,男，教授.E-mail:flcao@cjlu.edu.cn