LVDT校正技术研究
2016-06-17朱兆良
阮 健,朱兆良,李 胜,刘 奎
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
LVDT校正技术研究
阮健,朱兆良,李胜,刘奎
(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室,浙江 杭州 310014)
摘要:鉴于当前LVDT校正技术研究的不足,提出了一种基于支持向量机的LVDT校正技术,该项技术在全量程的范围内,提高传感器的线性度;同时消除LVDT的激励频率、物理参数和工作温度对LVDT输出的影响.在不同位置下,将不同激励频率、不同物理参数、不同工作温度与对应的输出信号作为训练数据,并将训练得到的基于支持向量机的校正模型取代传统的校正电路以实现校正目的.结果表明:此技术实现了预定的目标,以0~10 mm为全量程范围,其最大误差为0.125%.
关键词:LVDT;校正;支持向量机
差动变压器式位移传感器( 简称为LVDT) 是把直线位移转换为模拟电压的传感器,能进行非接触式位移测量,具有结构简单、响应速度快、分辨率高和使用寿命长等优点,因此被广泛应用于工业控制场合.LVDT的体积越大其线性范围越大,通过适当的算法可以有效的改善线性范围,从而在选择LVDT的型号时可以选择体积更小的LVDT,有利于在狭小空间上的应用.为了克服非线性特性,数字信号处理算法、离散模拟电路、傅立叶变换和人工神经网络技术等方式被用来改善LVDT的线性范围[1-5],数字信号处理算法、离散模拟电路和傅立叶变换等方法没有实现全量程范围内的线性化,且精度不高.人工神经网络技术虽然具有很强的非线性逼近能力, 但是其训练速度慢、容易陷入局部最小点、存在过拟合现象以及泛化能力较差等局限性使其难以达到预期精度.此外,LVDT的输出还受到LVDT的物理参数、激励频率和工作温度等参数的影响[6-8].为了克服已有研究的局限性,提出了一种基于支持向量机的LVDT校正技术,支持向量机是一种机器学习方法[9],建立在统计学习理论的基础上,采用结构风险最小化原则,提高了泛化能力,保证全局最优解,能够较好地解决小样本、非线性的问题,能在全量程范围内实现LVDT的线性化,且能消除LVDT的物理参数、激励频率和工作温度对LVDT输出的影响.
1LVDT的工作原理
LVDT被用于测量直线位移,它的工作原理类似于变压器.如图1所示,LVDT主要由铁芯、一个初级线圈和两个次级线圈组成,初级线圈与次级线圈间的互感量随铁芯位移的改变而改变,LVDT的两个次级线圈采样反向串接的方式,输出差动电压信号[10].
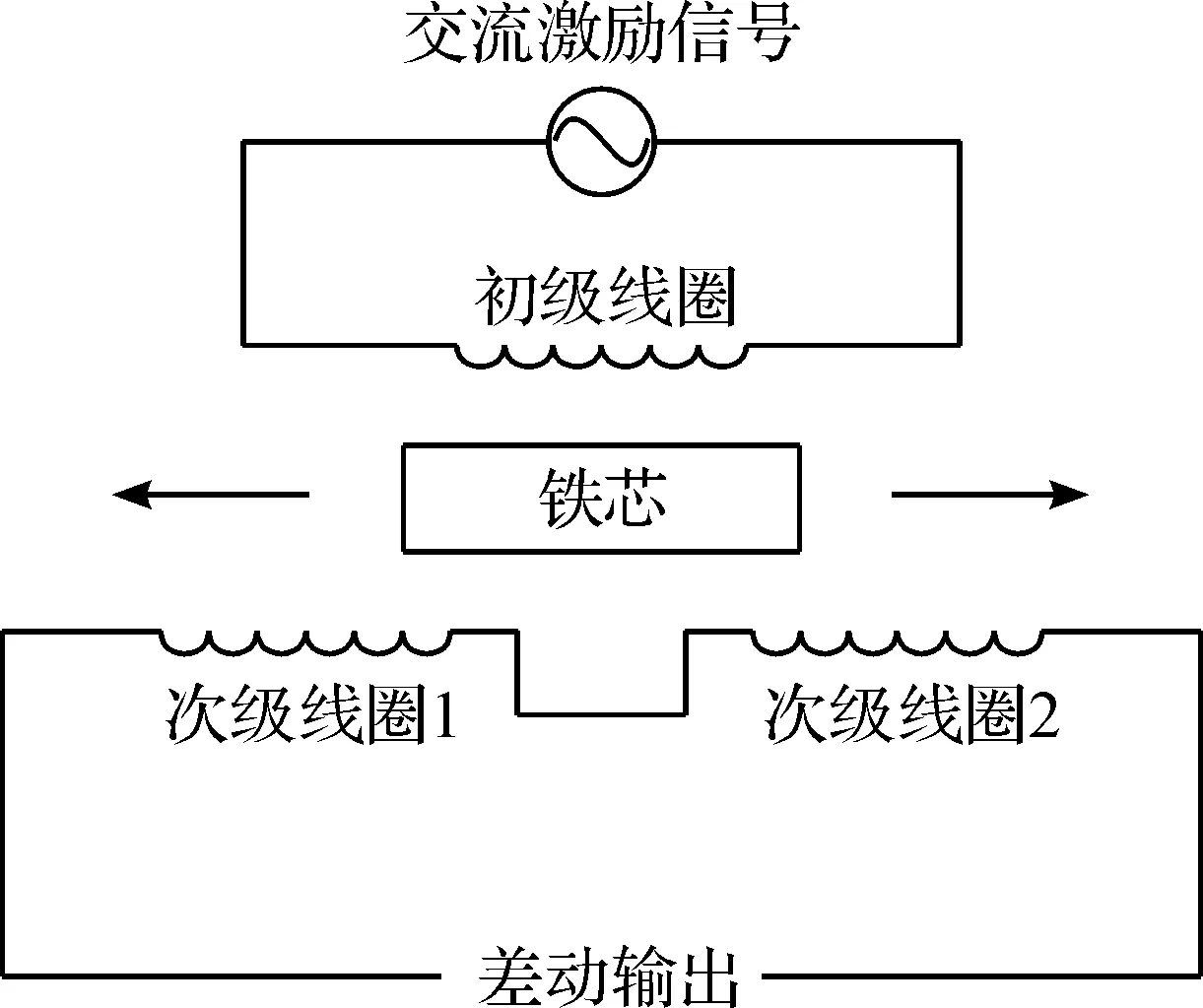
图1 LVDT的原理示意图Fig.1 Schematic diagram of LVDT
图2为LVDT的截面图,LVDT之间的关系式[9]分别为
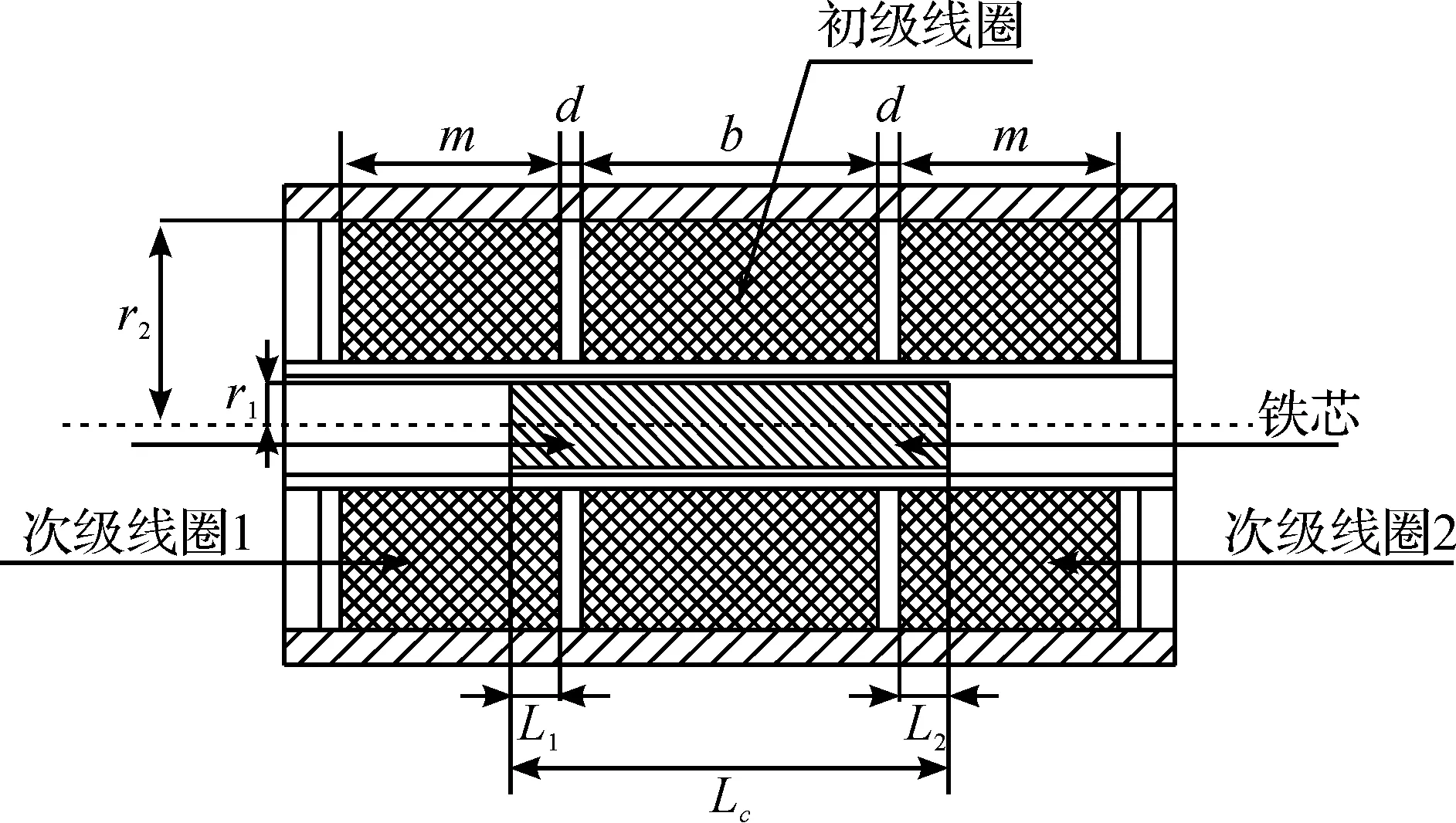
图2 LVDT的截面图Fig.2 Cross-section of LVDT
式中:Ip为初级线圈电流;np为初级线圈匝数;ns为次级线圈匝数;f为激励频率.
差分电压U为
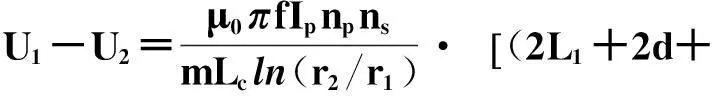
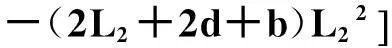
(1)
令铁芯在中位时,则
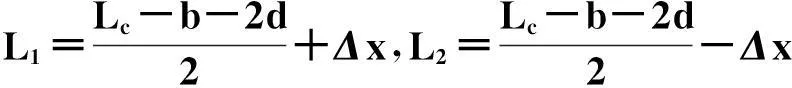
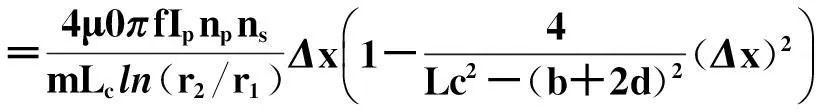
式中:μ0为真空磁导率,μ0=4π×10-7;vp为激励电压幅值;lp为初级线圈电感;Rp为初级线圈电阻.
线圈电感随环境温度的变化关系式为
Lt=Lt0(1+α(t-t0))
式中:Lt为t ℃时的电感值;Lt0为t0℃时的电感值;α为温度系数.
2LVDT测量技术所存在的问题
通过仿真说明目前LVDT测量技术所存在的问题,设3种不同的激励频率f分别为4,,5,6kHz;3种不同的r2与r1之比分别为2,3,4;3种不同的初级线圈匝数np分别为150,200,250;3种不同的次级线圈匝数ns分别150,200,250;3种不同的工作温度t分别为0,30,60 ℃,LVDT量程范围为0~10mm.借助MATLAB来仿真上述参数的变化对LVDT输出的影响,其结果分别如图3~7所示.
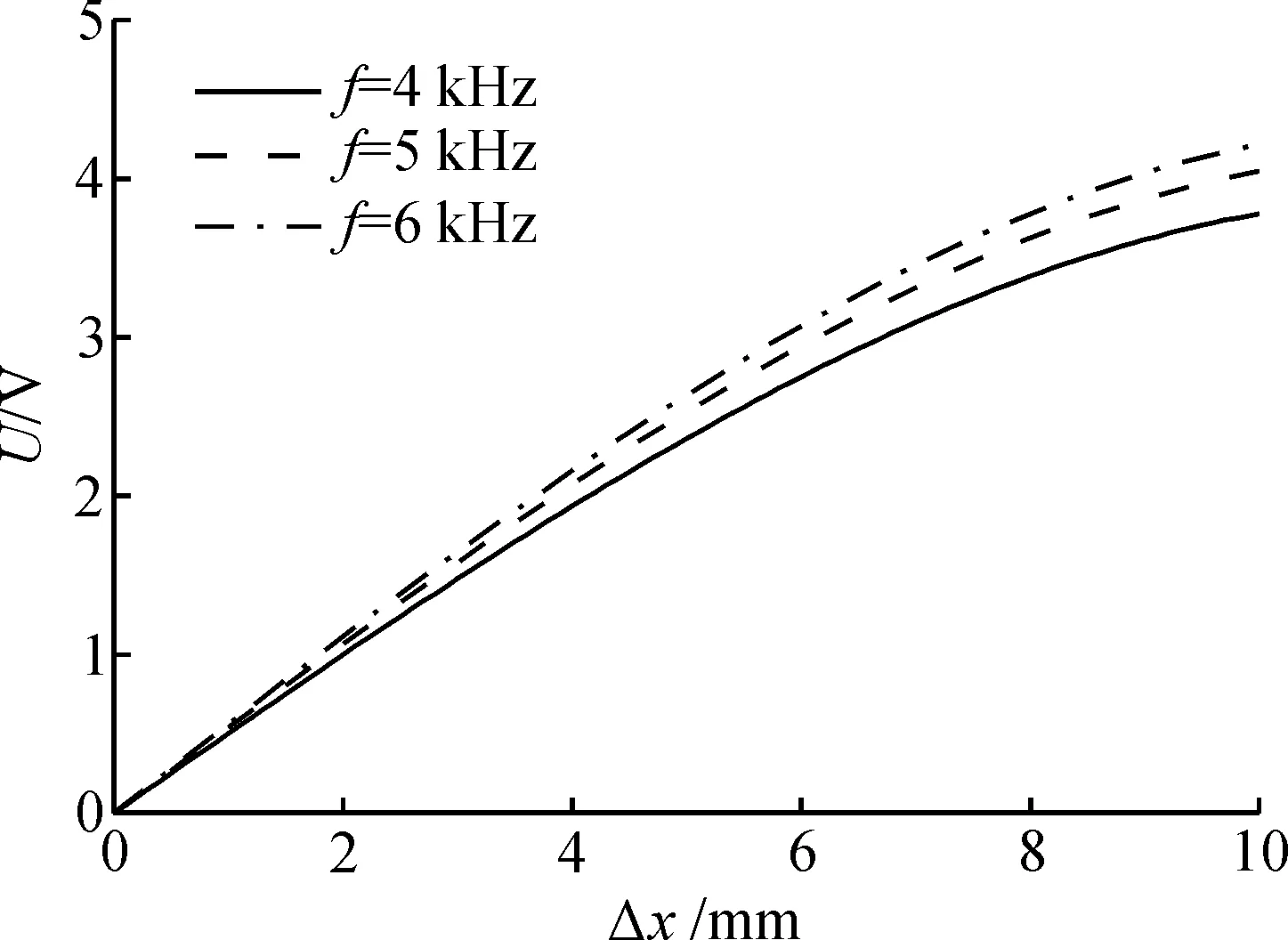
图3 激励频率f的变化对测量的影响Fig.3 Affect of frequency on measurement
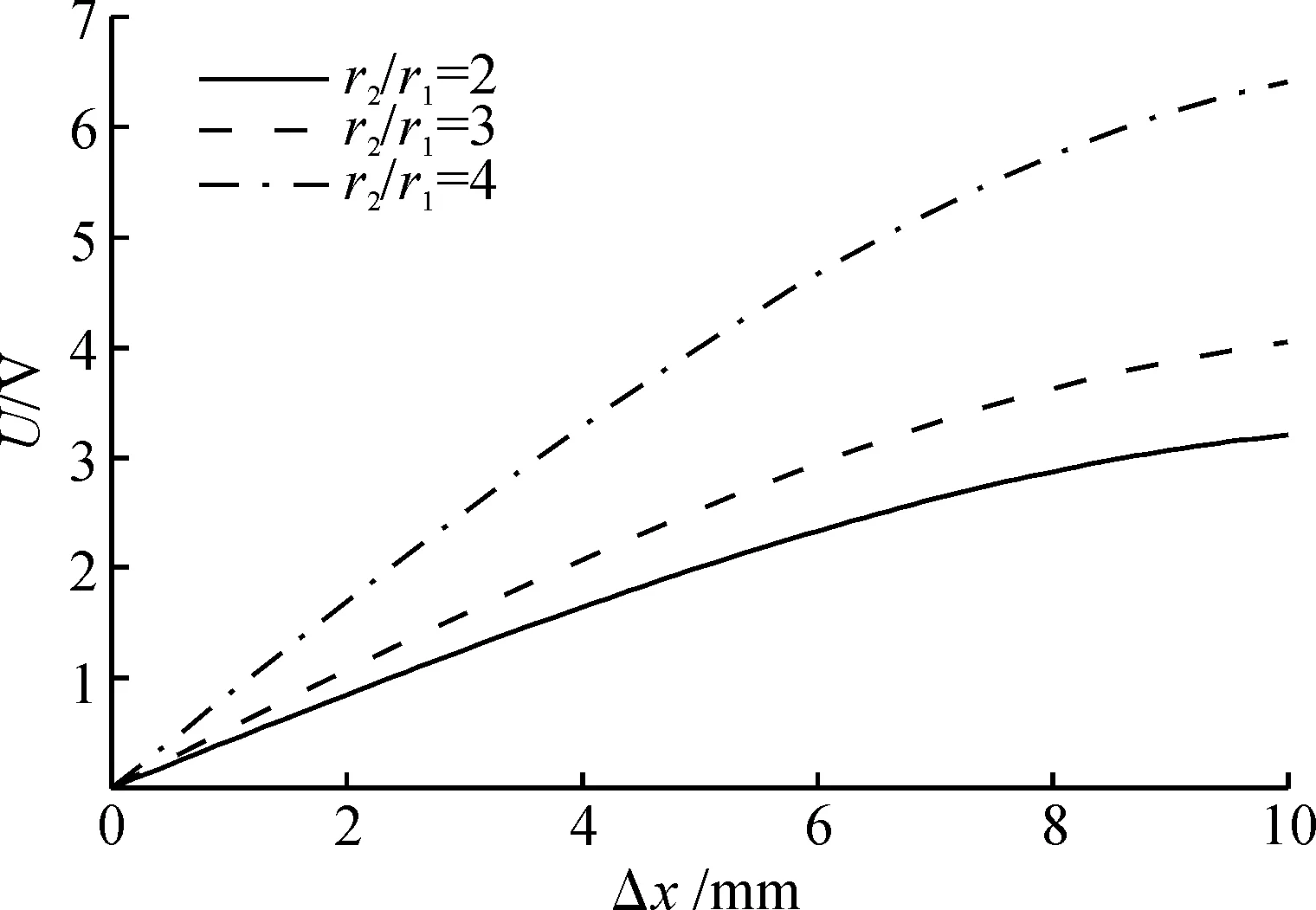
图4 r2/r1之比的变化对测量的影响Fig.4 Affect of r2/r1 on measurement
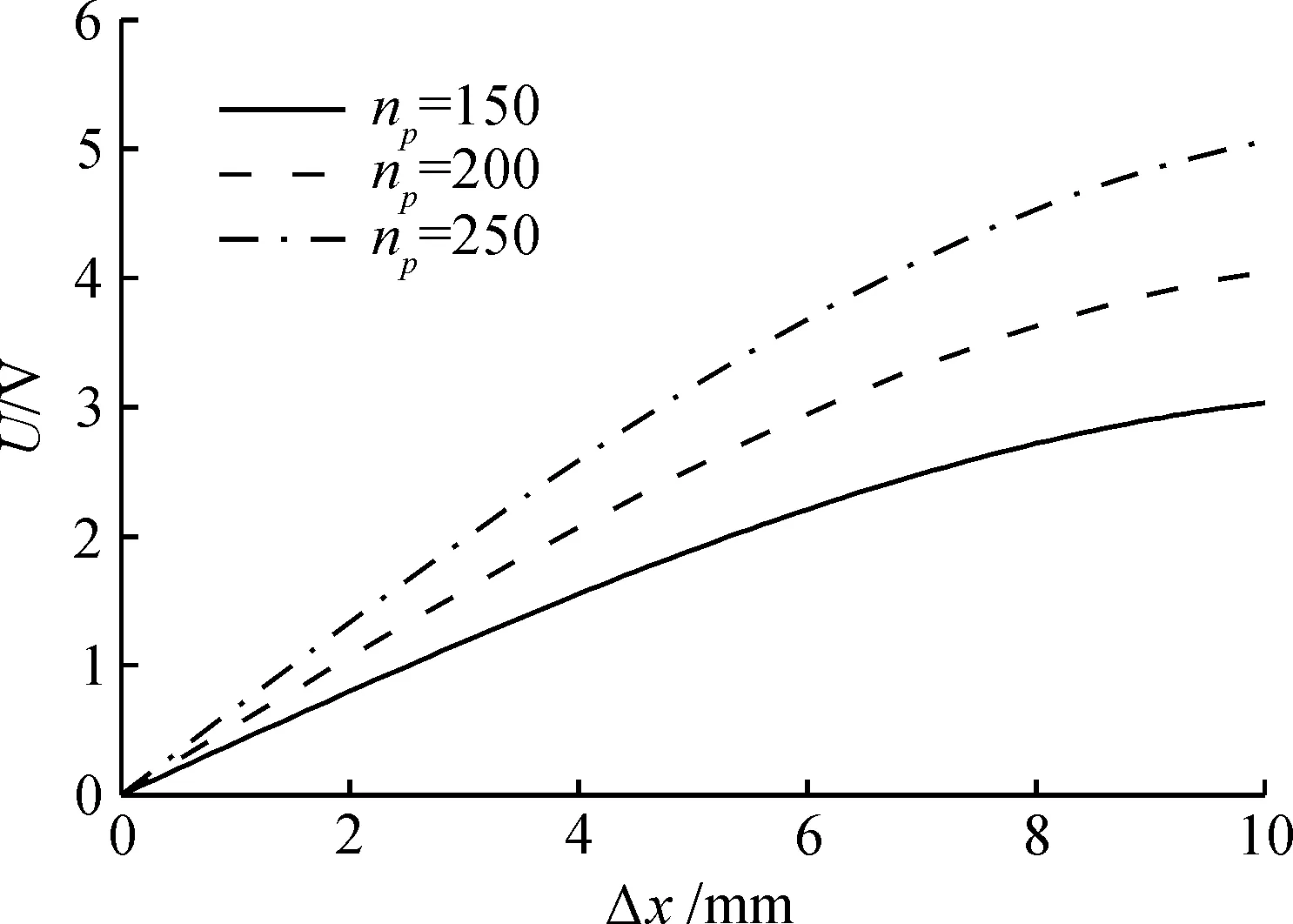
图5 np的变化对测量的影响Fig.5 Affect of np on measurement
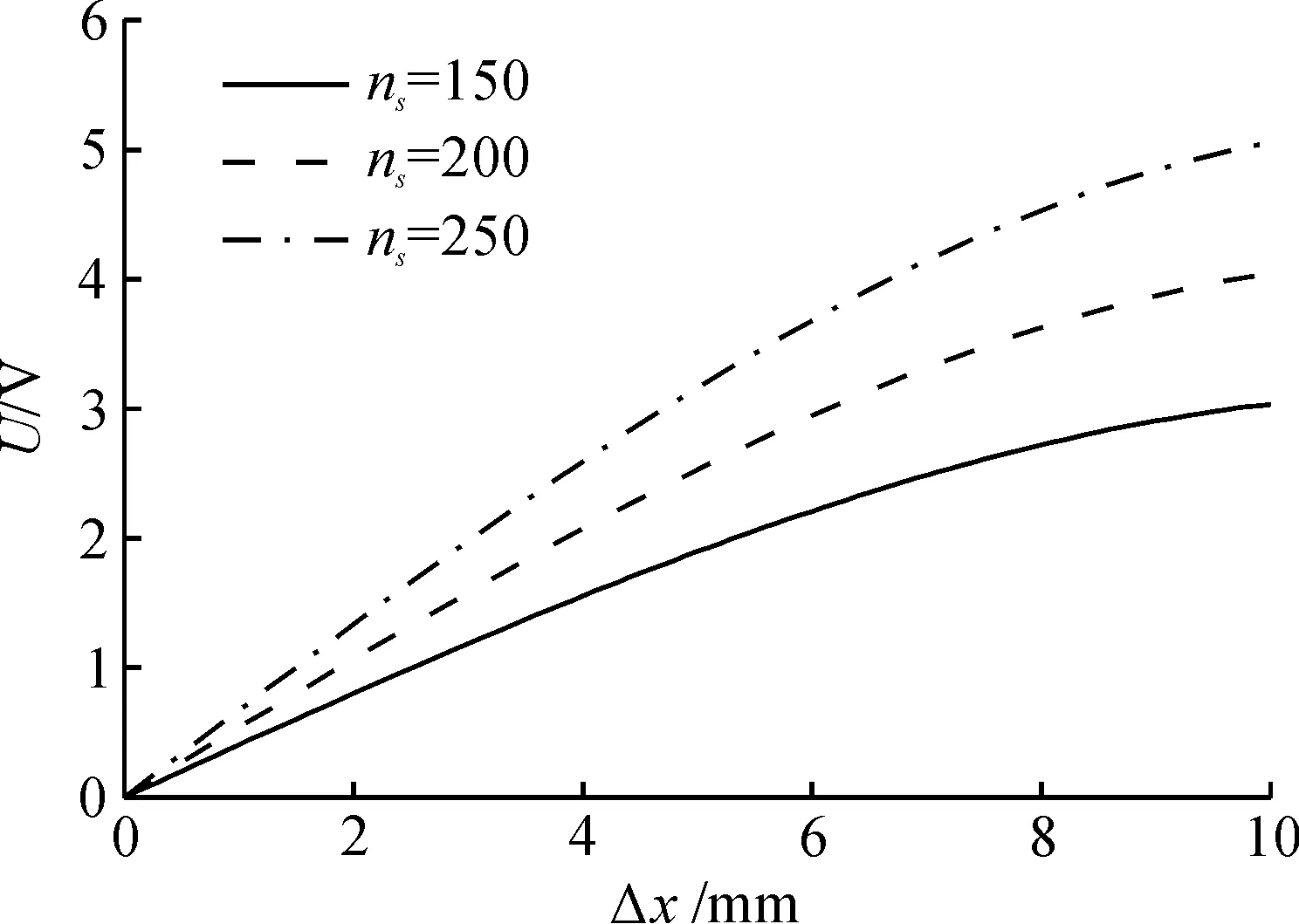
图6 ns的变化对测量的影响Fig.6 Affect of ns on measurement
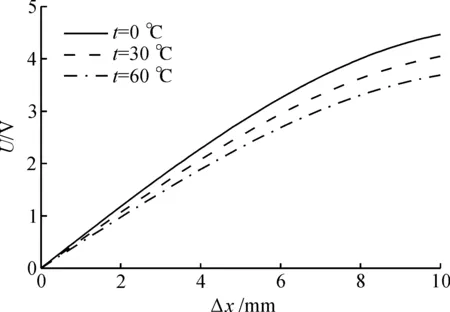
图7 t的变化对测量的影响Fig.7 Affect of t on measurement
3基于支持向量机的 LVDT校正技术
为了克服上述问题,提出了基于支持向量机的LVDT校正技术,其原理如图8所示,该技术通过添加训练得到的SVM校正模型以实现校正.
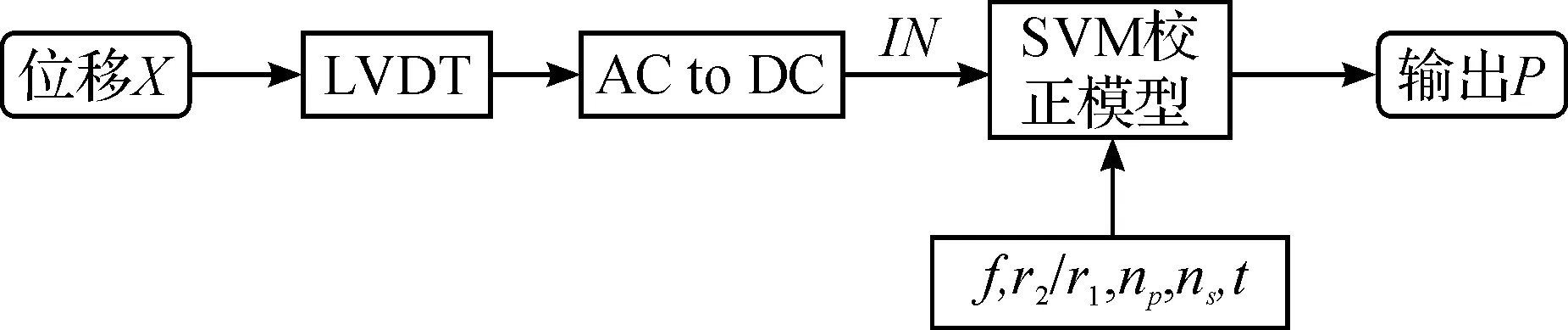
图8 基于支持向量机的LVDT校正原理示意图Fig.8 Schematic diagram of LVDT calibration technique based on support vector machine
基于支持向量机的LVDT校正技术,其实质是回归问题分析.支持向量机为回归问题的分析提供了框架,支持向量机校正模型的原理是:利用非线性映射将输入的数据映射到高维空间,在高维空间变换后进行回归分析[11-13],建立输入IN,f,r2/r1,np,ns,t和输出P的函数关系,因此LVDT校正可定义为如下的SVM回归问题.设采集的LVDT数据样本集为{xi,yi},i=1,2,…,n,其中,输入xi∈RN,需要求解的回归函数可表示为
f(x)=w·φ(x)+b
(2)
式中:w·φ(x)为w和φ(x)的内积;w为高维空间中的向量;φ(x)为SVM模型的输入函数;b∈R,为阀值.
为求解w与b,在实际应用中引入松弛变量ξ,ξ*≥0,将式(2)转换为优化问题:
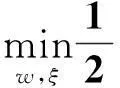
(3)
约束条件为
式中:i=1,2,…,n;C为惩罚系数,C越大表示对训练误差大于ε的数据样本的惩罚越大;ε规定了回归函数与输出的误差要求,ε越小,回归函数与输出的误差越小,估计精度越高.
在求解式(3)所述优化问题时,引入Lagrange算子α和α*,将式(3)的优化问题转换为其对偶形式进行求解[14-15],即
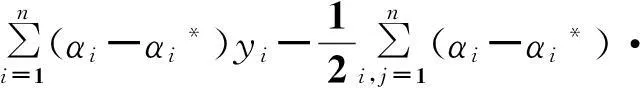
(αj-αj*)〈φ(xi)·φ(xj)〉-
约束条件为
式中〈φ(xi)·φ(xj)〉为高维空间的点积运算,函数φ是未知的高维函数.SVM只考虑高维特征空间的点积运算K(xi,xj)=〈φ(xi)·φ(xj)〉,不直接使用函数φ,从而有效地解决了这个问题.K(xi,xj)称为核函数,满足Mercer条件的对称函数均可作为核函数.笔者选用的是径向基核函数(RBF).
求得α值有
确定回归函数为
根据Karush-Kuhn-Tucker条件,计算得
式(3)中C的大小直接影响到误差的大小,而C值的选择很难用理论方法确定[16-17].笔者采用的调节参数的准则是:检查某特定加权的修正是否确实减小了误差,如果产生了超调,那么C就减小;若连续几步迭代都是降低误差,则C值就增加一个量.C参数调节自适应关系式为

式中:Δe为每次迭代的误差变化;a,b均为常数.
4仿真结果
当SVM训练结束后,用训练得到的SVM校正模型来测试模型效果,令位移实际值(输入量)范围为0~10mm,参数f,r2/r1,np,ns,t在各自范围内随机选取,其中参数f限定范围在4~6kHz,r2/r1限定范围在2~4,np限定范围在150~250, ns限定范围在150~250,t限定范围在0~60 ℃,在参数随机选取下,位移测量值(输出量)与位移实际值(输入量)之间的关系如图9所示,位移测量值(输出量)与位移实际值(输入量)的误差与位移实际值的关系如图10所示,表1为LVDT校正技术部分的仿真结果.
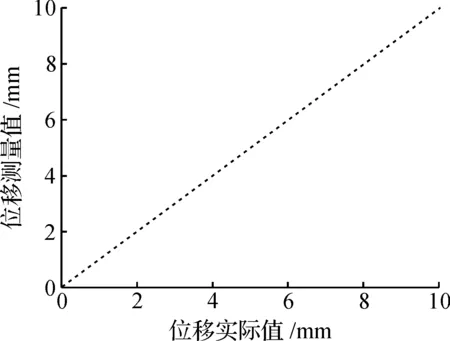
图9 位移测量值与位移实际值的关系图Fig.9 Measured vs actual displacement graph
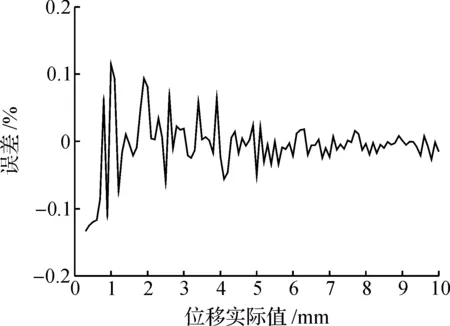
图10 误差与位移实际值的关系图Fig.10 Error vs actual displacement graph
由图10和表1可知:在以0~10 mm 为全量程范围,参数f,r2/r1,np,ns,t在各自范围内随机选取的情况下,基于支持向量机的LVDT校正技术的最大误差为0.125%,故此技术不仅能实现全量程范围内的线性化,而且能消除参数f,r2/r1,np,ns,t对LVDT输出的影响,能很好的实现目标要求.
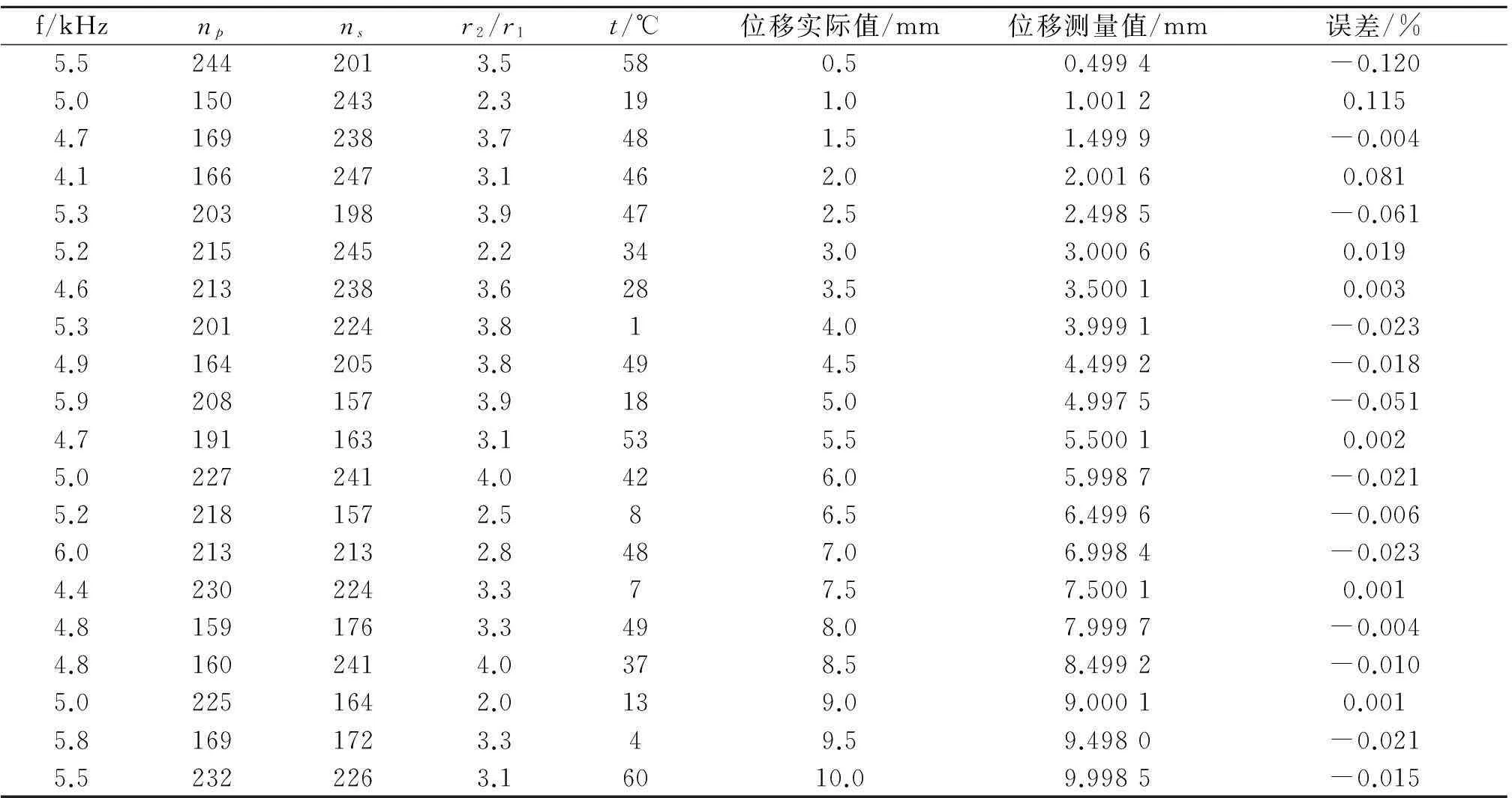
表1 LVDT校正技术的部分仿真结果
5结论
目前,研究者们所提出的校正技术的有效性仅限于部分的量程范围,另外,当LVDT的物理参数、激励频率或者工作温度发生变化时,都得进行重新校准而笔者所提出的基于支持向量机的校正技术能够在全量程的范围内,提高LVDT的线性度;另外,当LVDT的物理参数、激励频率和工作温度发生变化时,测量系统依然能保持测量的准确度,故此技术对工程应用具有重要的参考价值.
参考文献:
[1]FORD R M, WEISSBACH R S, LOKER D R. A novel DSP-based LVDT signal conditioner[J]. Instrumentation & measurement IEEE transactions on,2001,50(3):768-773.
[2]MISHRA S K, PANDA G. A novel method for designing LVDT and its comparison with conventional design[C]//Sensors Applications Symposium. Proceedings of the 2006 IEEE. Houston: IEEE,2006:129-134.
[3]DRUMEA A, VASILE A, COMES M, et al. System on chip signal conditioner for LVDT sensors[C]// Electronics Systemintegration Technology Conference. Dresden: IEEE,2006:629-634.
[4]WANG Z, DUAN Z. The research of LVDT nonlinearity data compensation based on RBF neural network[C] // World Congress on Intelligent Control & Automation.Chongqing: IEEE,2008:4591-4594.
[5]WANG L, WANG X, SUN Y. Intelligent acquisition module for differential transformer position sensor[C]//Intelligent System Design and Engineering Application:2010 International Conference on IEEE.Changsha: IEEE,2010:878-883.
[6]YUN D, HAM S, PARK J, et al. Analysis and design of LVDT[C]// Ubiquitous Robots and Ambient Intelligence (URAI):2011 8th International Conference.Incheon: IEEE,2011:836-837.
[7]MACIONE J, NESBITT S, PANDIT V, et al. Design and analysis of a novel mechanical loading machine for dynamic in vivo axial loading[J]. Review of scientific instruments,2012,83(2):225-235.
[8]GROSZKOWSKI J. The temperature coefficient of inductance[J]. Radio engineers proceedings of the institute,1937,25(4):448-464.
[9]张学工.关于统计学习理论与支持向量机[J].自动化学报,2000,26(1):32-42.
[10]刘志才.LVDT位移传感器数字信号处理算法及电路研究[D].杭州:浙江大学,2012.
[11]白鹏,张喜斌,陈长兴.基于支持向量机的压力传感器校正模型[J].空军工程大学学报(自然科学版),2007(5):37-40.
[12]CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J]. Transactions on intelligent systems & technology,2007,2(3):389-396.
[13]SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural processing letters,1999,9(3):293-300.
[14]GESTEL T V, SUYKENS J A K, BAESENS B, et al. Benchmarking least squares support vector machine classifiers[J]. Machine learning,2004,54(1):5-32.
[15]白鹏,刘君华.基于多维光谱的多组分混合气体浓度支持向量机算法[J].化工自动化及仪表,2005,32(5):43-47.
[16]阮秀凯,张志涌,尹立鹤.基于ε-支持向量回归机的信道估计[J].浙江工业大学学报,2010,38(3):263-267.
[17]郑莉莉,黄鲜萍,梁荣华.基于支持向量机的人体姿态识别[J].浙江工业大学学报,2012,40(6):670-675.
(责任编辑:陈石平)
Research on calibration technique of LVDT
RUAN Jian, ZHU Zhaoliang, LI Sheng, LIU Kui
(Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology, Ministry of Education, Zhejiang University of Technology, Hangzhou 310014, China)
Abstract:Due to the deficiency of the current research on calibration technology of LVDT, a calibration technique using Support Vector Machine (SVM) for LVDT is proposed in this paper. The aim of this technique is to improve the linearity of LVDT in the full range as well as eliminate the effect of excitation frequency, physical parameters and working temperature on the output of LVDT. The system once designed is subjected to test data with variations in excitation frequency, physical parameters and working temperature for particular displacement. The conventional calibration circuit is replaced by SVM model to achieve desired objectives. Results show the proposed technique has achieved its set objectives. The proposed calibration technique yields the maximum error of 0.125%, with linearization over the range 0 to 10 mm.
Keywords:LVDT; calibration; support vector machine
收稿日期:2015-11-11
基金项目:国家自然科学基金资助项目(51375445)
作者简介:阮健(1963—),男,福建福安人,教授,博士生导师,研究方向为电液控制技术,E-mail:yanyan333@126.com.
中图分类号:TH137
文献标志码:A
文章编号:1006-4303(2016)02-0184-05
