电磁智能车电感排布方案

陈国定,张晓峰,柳正扬

(浙江工业大学 信息工程学院，浙江 杭州 310023)



电磁智能车电感排布方案

陈国定,张晓峰,柳正扬

(浙江工业大学 信息工程学院，浙江 杭州 310023)

摘要：电磁智能车利用垂直于赛道中心线的电感感应电动势大小来判断路径，而智能车在不同的赛道元素上行驶时，电感与赛道中心线存在夹角，其感应电动势的大小并不等效于在赛道中心线垂直方向上的感应电动势，导致计算小车位置偏差时出现误差，并且在直角弯等赛道元素处易产生误判.针对这个问题，提出了一种新的电感排布方案——“双T型”电感排布方案，通过两个相互垂直的电感检测到的感应电动势计算出小车与赛道中心线的夹角，解算在出赛道中心线垂直方向上等效电感的感应电动势，很好地解决了直角弯等的识别问题.

关键词：电磁；智能车；感应电动势；电感排布方案

智能车竞赛电磁组的赛道中心敷设一根电磁线，其中通有20 kHz，100 mA的交变电，智能车利用电磁感应原理检测其产生的交变磁场来判断路径，控制小车沿赛道行驶[1].由毕奥-萨伐定理[2]可知：小车前端排布的水平电感检测到的感应电动势会随小车远离载流电磁线而减小，从而可以反映出小车与赛道中心线的偏离距离.目前的巡线算法基本都是建立在水平电感始终垂直赛道中心线的基础上，通过其感应电动势的变化来计算小车的偏离距离.而实际在大部分的赛道元素中，水平电感都不完全垂直于赛道中心线，从而导致计算得到的偏离距离与实际存在偏差，在直角弯处甚至会引起误判，严重影响比赛成绩[3].因此，电感排布方案是制约电磁智能车竞赛成绩的关键因素之一.

针对上述问题，笔者提出了一种新的电感排布方案——“双T型”电感排布方案，通过两个相互垂直的电感检测到的感应电动势，计算出小车与赛道中心线的夹角，解算在出赛道中心线垂直方向上等效电感的感应电动势，降低了在直角弯处的误判率，显著提高了智能车的速度和稳定性.

1电磁智能车信号检测模型分析

1.1信号检测原理

智能汽车竞赛电磁组赛道中心用于路径导航的20 kHz交变电流所产生的电磁波属于甚低频电磁波.甚低频频率范围处于工频和低频中间，为3～30 kHz，波长为100～10 km[4]，如图1所示.

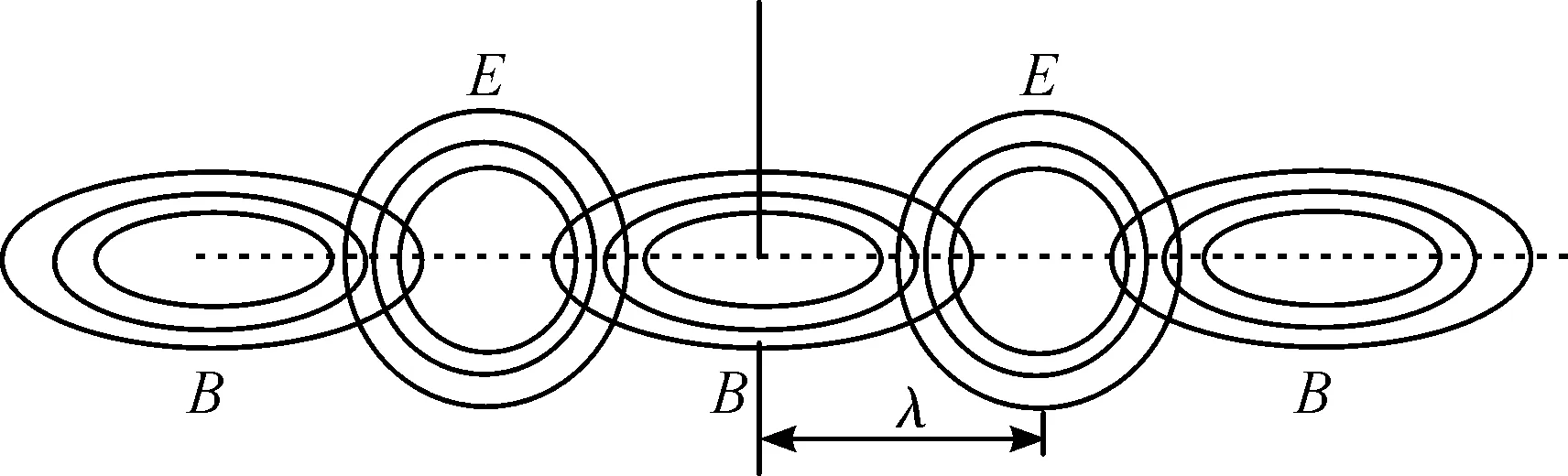
；λ—波长；c—光速；f—频率图1　载流电磁线周围的电磁场示意图Fig.1　Schematic diagram of the electromagnetic field around current

由于赛道导航电线和小车尺寸l远远小于电磁波的波长λ，电磁场辐射能量很小，所以能够感应到电磁波的能量非常小.为此，将导线周围变化的磁场近似为缓变的磁场，按照检测静态磁场的方法获取导线周围的磁场分布，从而进行位置检测[4].而感应磁场的分布是以载流电磁线为轴的一系列的同心圆.圆周上的磁场强度大小相同，并随着距离载流电磁线的半径r增加成反比下降[5].

1.2信号检测模型

为了论述方便，对智能车及所在赛道建立如图2所示的坐标系[6].假设沿着跑道前进的方向为z轴，则垂直跑道往上为y轴，在跑道所在平面内垂直于跑道中心线为x轴，xyz轴满足右手定则[7].约定文中提到的“车模与赛道中心线的距离”均表示左右两组电感的中点与赛道中心线的距离.

由于磁场分布是以z轴为中心的同心圆，所以在计算磁场强度的时候可仅仅考虑坐标(x,y).因为电感的轴线是水平的，所以感应电动势反映了磁场的水平分量，跑道中心的电磁线对于电感均可等效为无限长直导线，根据毕奥-萨伐定理易得单个电感感应电动势大小与h/(h2+x2)成正比，即感应电动势[7]为

(1)

式中K为比例系数.

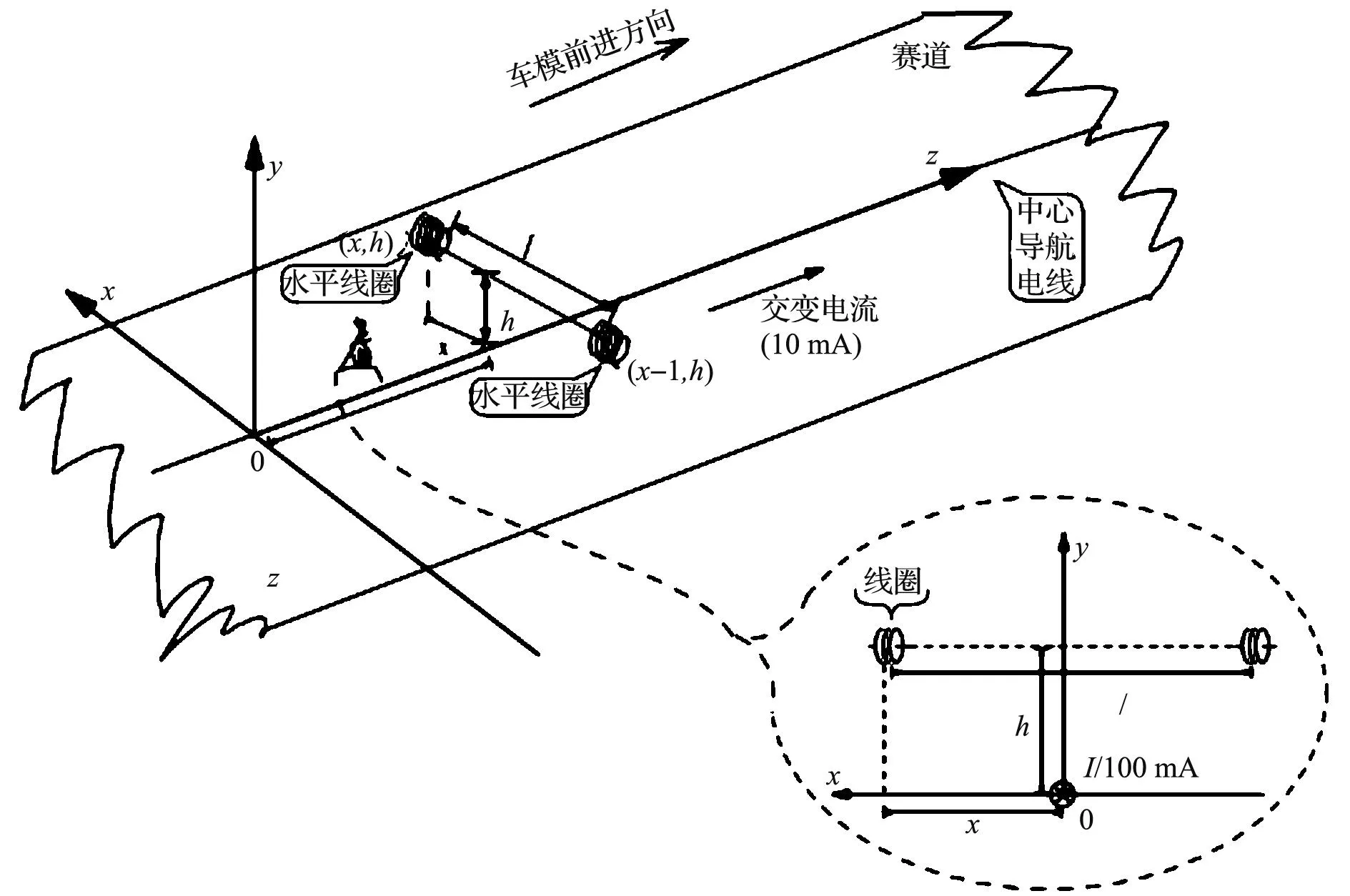
图2　赛道坐标系与电感布置初步方案Fig.2　Track coordinate system and inductance placement simple scheme

2常用电感排布方案及其局限性

2.1双水平电感排布方案及其局限性

常用的双水平电感排布方案结构如图3所示，在智能车前方，距离地面高度h处水平方向排布两个相距L的工字电感，两个电感的轴线在同一水平线上.图3中赛道中心线用灰色粗实线画出，后续图中同此.

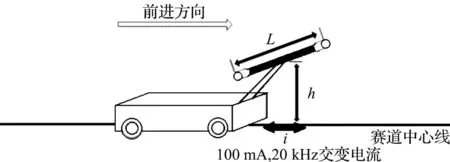
图3　双水平电感排布方案Fig.3　Double level inductance placement scheme

设两个电感之间的中点坐标为(x,y)，则左边电感的坐标为(x-L/2,h)，感应电动势为E1，右边电感的位置(x+L/2,h)，感应电动势为E2，由式(1)得

(2)

(3)

式中：E1和E2可通过电感检测得到；α为电感在赛道上的投影与赛道中心线的夹角，当电感与赛道中心线垂直时，sinα=1.

进一步可得赛道中心线垂直方向上的感应电动势为

(4)

(5)

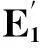
2.1.1弧形弯处无法计算小车与赛道中心线的夹角α

小车在直道上行驶时，左右电感始终与赛道中心线垂直，即sinα=1恒成立.而当小车进入弧形弯道时，夹角α的大小随着小车的行驶不断改变，通过两个水平电感无法计算出α的大小，如图4所示.这个时候，只能判断出小车当前的偏离方向，无法精确地计算出偏差量，从而不能给出准确的控制量，引起误判断，极大地影响了小车行驶的稳定性.

图4　双水平电感排布在弧形弯道处Fig.4　Double level inductance placement scheme in the curved track

2.1.2直角弯处无法识别方向

小车在直角弯处的情况如图5所示，x和y两个方向的导线对于电感均等效为射线.

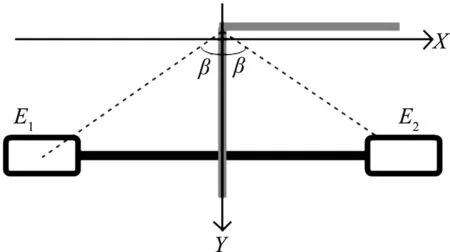
图5　双水平电感排布在直角弯处Fig.5　Double level inductance placement scheme in the orthogonal track

从图5上可以看到：水平放置的电感与x轴方向导线垂直，与y轴方向导线方向平行，即αx=90°,αy=0°,且x=0，可得

(6)

(7)

式中：E1x，E2x分别为左右电感于x方向导线的感应电动势；E1y，E2y分别为左右电感于y方向导线的感应电动势，下同.

因而，进一步可得

(8)

(9)

即

(10)

从式(8)可得：在直角弯处，左右电感的感应电动势值相等，因此无法识别方向.

2.2“八”字形电感排布方案及其局限性

“八”字形电感排布即在双水平电感排布方案的基础上，将左右两个电感分别逆时针和顺时针旋转相同的角度θ，如图6所示.

图6　“八”字形电感排布示意图Fig.6　The slant inductance placement scheme

小车在直道上行驶时，有

(11)

(12)

由于θ已知，所以和双水平电感排布方案一样，在直道上可以通过比较E1和E2的大小判断出小车与赛道中心线的偏离方向及偏差量，并做出相应的方向控制.

在直角弯处的情况如图7所示，可得

(13)

(14)

又β∈(0，π)，故

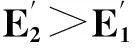
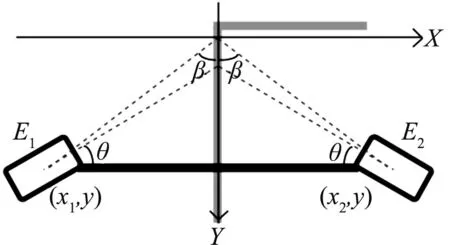
图7　“八”字形排布在直角弯道处Fig.7　The slant inductance placement scheme in the orthogonal track

在弧形弯道处的情况则如图8所示，左右两侧电感和赛道中心线切线所成夹角分别为α1，α2.

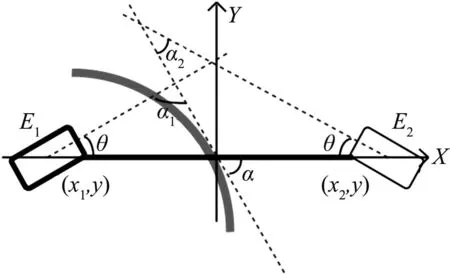
图8　“八”字形电感排布在弯道处Fig.8　The slant inductance placement scheme in the curved track

由图8可得

(15)

(16)

进一步可得赛道中心线垂直方向上的感应电动势为

(17)

(18)

虽然θ已知，但是依旧不能计算出α的大小，无法给出准确的控制量，影响了小车行驶的稳定性[7].

3“双T型”电感排布方案的实现

针对以上两种方案存在的局限性，提出了一种新的电感排布方案——“双T型”电感排布方案,即在双水平排布的基础上，两侧分别增加了一个与水平电感垂直的竖直电感，其结构如图9所示.需要说明的是，由于实际情况中互为垂直的两电感间距很小，故在计算上可以将两电感视为在同一空间位置上.

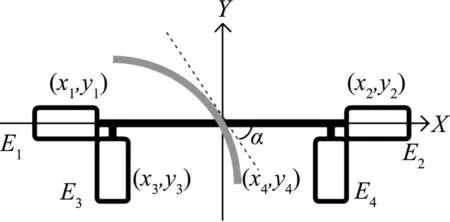
图9　“双T型”电感排布示意图Fig.9　The double-T inductance placement scheme

水平电感和竖直电感两两垂直，若以导线的交点为原点，水平方向为x轴，竖直方向为y轴建立直角坐标系.设电感的坐标为(xi,yi)(其中i=1,2,3,4,分别表示4个电感)，感应电动势的大小分别为E1,E2,E3,E4,从而可得到小车与赛道中心线夹角的正切值为

(19)

进一步可得夹角为

(20)

从而就可以准确地计算得到赛道中心线垂直方向上的感应电动势为

(21)

(22)

而在直角弯道处的情况如图10所示，同样以水平电感与赛道中心载流导线的交点为原点，水平方向为x轴，竖直方向为y轴建立直角坐标系.设电感的坐标为(xi,yi)(其中i=1,2,3,4,分别表示4个电感)，感应电动势的大小分别为E1,E2,E3,E4,则有

|x1|=|x2|

(23)

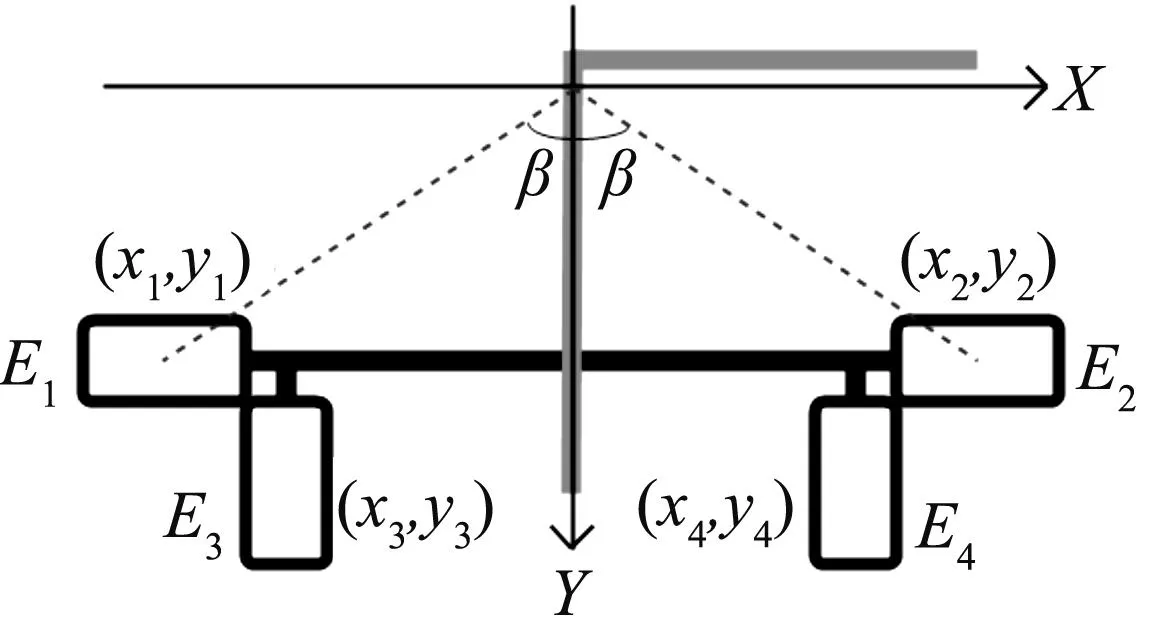
图10　“双T型”电感排布在直角弯道处Fig.10　The double-T inductance placement scheme in the orthogonal track

又两个水平电感与x轴平行，其感应电动势的大小只与y轴方向导线有关.两个竖直电感与y轴平行，其感应电动势的大小只与x轴方向导线有关.由此可得

E1=E2

(24)

(25)

(26)

显然，E4>E3，应对小车进行右转控制，从而识别了直角弯处的方向.

因此，采用“双T型”电感排布方案不仅能计算出小车与赛道中心线的夹角，解算在出赛道中心线垂直方向上等效电感的感应电动势，同时也能准确地识别直角弯，很大程度上提高了方向控制的准确性.

4实验及结果

为了验证“双T型”电感排布方案，可以通过两对相互垂直的电感检测到的感应电动势计算出小车与赛道中心线的夹角，从而解算在出赛道中心线垂直方向上等效电感的感应电动势，搭建了一台实验用的智能车[8-9]，严格按照“双T型”方案进行电感排布，并且测量出该智能车的左右两组电感间距L=0.21 m，电感距离赛道平面高度h=0.2 m，取比例系数K=40.

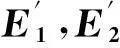
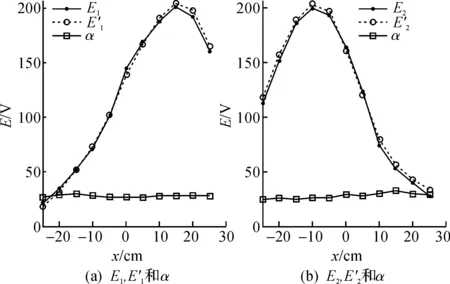
图11　α=30°时E1,E2和的比对以及计算所得的αFig.11　

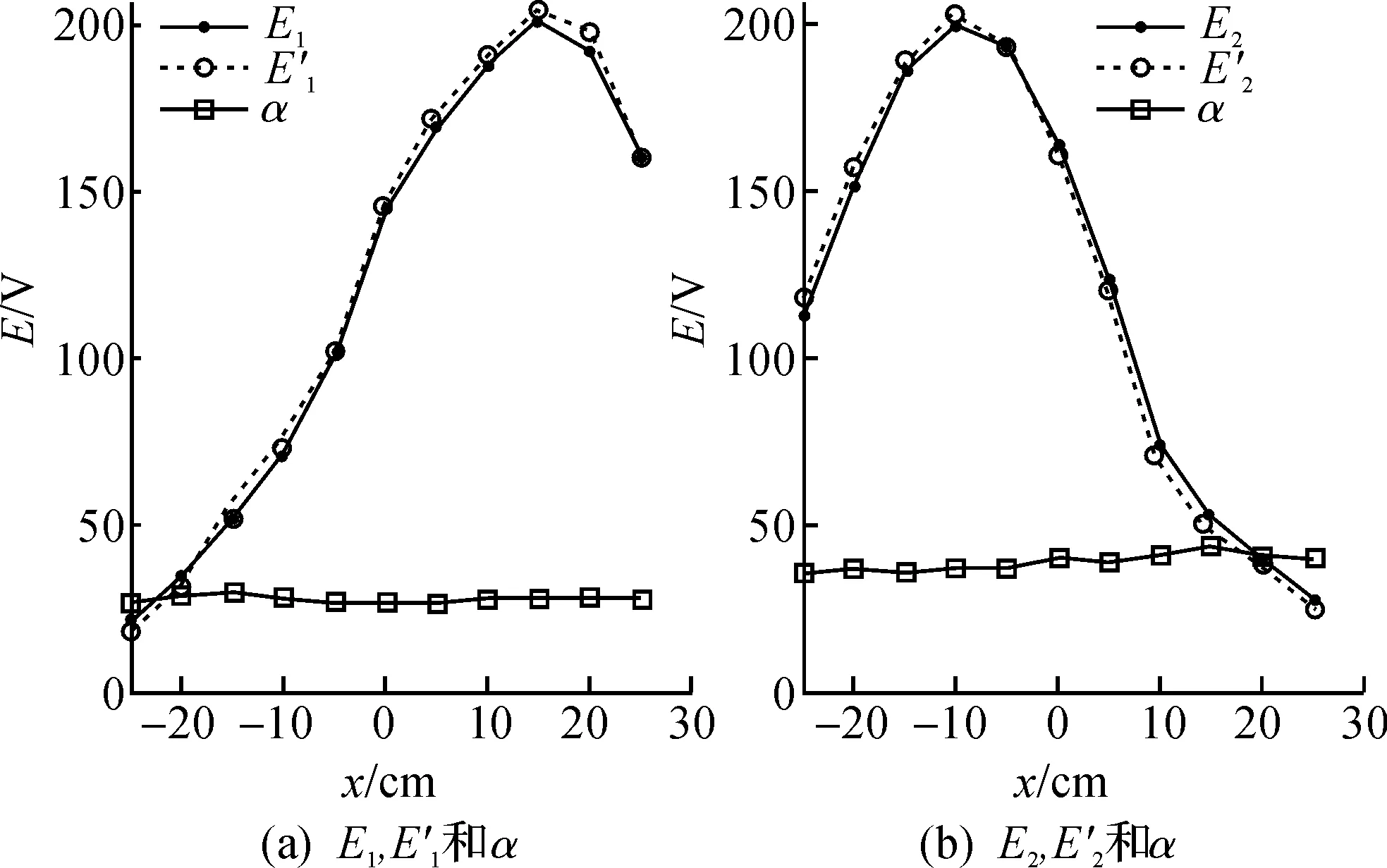
图12　α=45°时E1，E2和的比对以及计算所得的αFig.12　

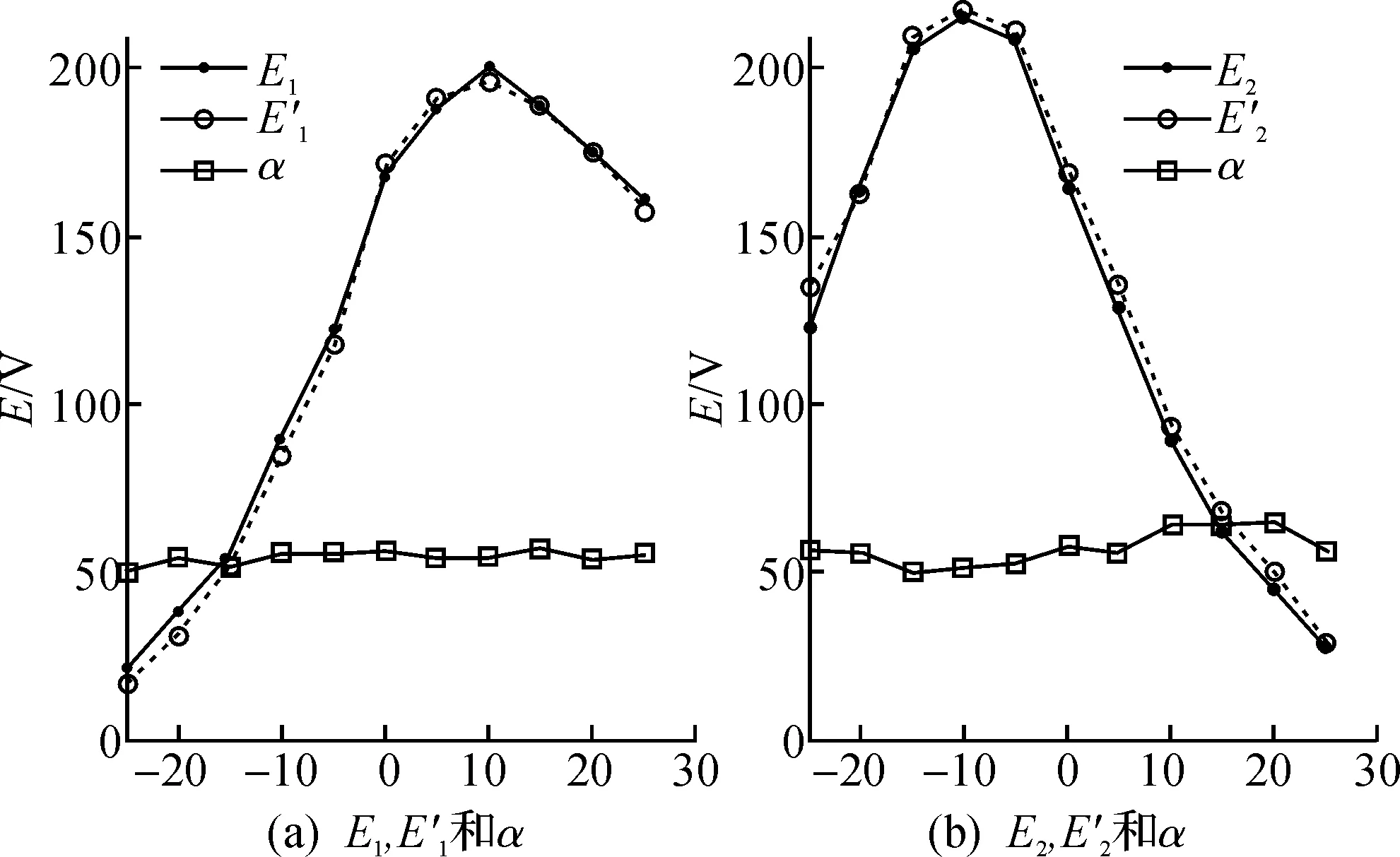
图13　α=60°时E1，E2和的比对以及计算所得的αFig.13　

5结论

对电磁智能车常用电感排布方案的局限性详细分析后进行改进，提出了“双T型”电感排布方案.实验证明，该方案可以弥补现有方案的不足，优化了电磁智能车路径检测，确保智能车能平稳、快速地运行.

参考文献：

[1]竞赛秘书处.电磁组竞赛车模路径检测设计参考方案[EB/OL].[2010-01-10].http://www.smartcar.au. tsinghua.edu.cn/.

[2]施建青.大学物理学(下册)[M].北京:高等教育出版社,2009:10-11.

[3]王能才.基于电磁导航的智能车信号检测与控制策略研究[D].兰州:兰州理工大学,2014.

[4]陈军,高雅.电磁智能车二值离散式磁场检测系统设计[J].洛阳师范学院学报,2013,32(8):21-23.

[5]王宇,董辉,徐建明，等.一种新的智能小车控制策略[J].浙江工业大学学报,2012,40(2):217-221.

[6]唐昊,刘海刚,刘群，等.电磁智能小车控制算法设计[J].实验室科学,2014,17(4):67-71.

[7]张晓峰,钟一博,李清晨，等.电磁智能车循迹算法[J].计算机系统应用,2014,23(12):187-190.

[8]陈国定,钟引帆,揭飞.非隔离光伏并网逆变器共模电流抑制研究[J].浙江工业大学学报,2015,43(6):655-659.

[9]董辉,高阳,张文安，等.基于增强微分器的永磁同步电机速度控制研究[J].浙江工业大学学报,2015,43(4):445-449.

(责任编辑：陈石平)

The inductance placement scheme of electromagnetic intelligent vehicle

CHEN Guoding, ZHANG Xiaofeng, LIU Zhengyang

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Electromagnetic intelligent vehicle determines the track by using the induced electromotive force which is perpendicular to the centerline of track. However, when intelligent car runs on different track elements, there is an angle between the axis of inductance and centerline of the track, so the induced electromotive force on the inductance is not equivalent to the vertical component. This will cause position calculation deviation and it is likely to make wrong decisions in right-angle track element. A new double T inductance placement scheme is proposed to deal with this problem. The induced electromotive force detected in two mutually perpendicular inductances is used to calculate the angle between the axis of inductance and centerline of the track, the equivalent inductance of the induced electromotive force on the vertical direction of the centerline of the track can be calculated. It can solve the identification problem at right-angle track effectively.

Keywords:electromagnetic; intelligent vehicle; induced electromotive force; inductance placement scheme

收稿日期：2015-10-15

基金项目：浙江省自然科学基金资助项目(LY15F030015)

作者简介：陈国定(1962—)，男，浙江宁波人，教授，博士，研究方向为计算机先进控制、网络控制、电力电子与电力传动及控制策略等，E-mail:gdchen@zjut.edu.cn.

中图分类号：TP273

文献标志码：A

文章编号：1006-4303(2016)02-0124-05