在小学图形与几何知识的教学中培养学生动手操作的做法

陈兰

【摘要】《数学课程标准》指出，小学数学教学活动的开展要贴近学生的实际，有利于学生体验与理解、思考与探索。在教学中教师要重视直观，处理好直观与抽象的关系；要重视直接经验，引导学生动手、动脑，参与知识的形成过程。学生创新意识的培养是现代数学教育的基本任务，应体现在数学教与学的过程之中。

【关键词】图形 观察 操作 思维

【中图分类号】G623.5 【文献标识码】A 【文章编号】2095-3089（2016）04-0124-01

《小学数学课程标准》在修订时突出了动手操作在小学数学教学活动中的地位和作用，强调要根据儿童的年龄特征和认知规律，通过实践操作，使学生更好地掌握所学内容。

几何知识发展的基本历史是从直观到论证。小学生对图形地认识还属于直观阶段。因此，在小学图形知识的教学中，就必须采用“看一看、折一折、剪一剪、拼一拼”等操作，让学生通过亲自触摸、观察和实验等，获得直接的体验，领会知识。下面谈一谈我在图形知识的教学中培养学生动手操作的做法。

一、教师示范操作，学生通过观察得出操作方法。

小学生的认知结构是由感性开始，从形象思维向抽象思维的过渡阶段，直观是过渡的桥梁，它为运用感性认识获取理性认识，从形象思维向抽象思维过渡提供条件。

在教学轴对称图形时，二年级的学生年龄小、生活阅历浅，他们对“对折”和“完全重合”理解有困难，这正是轴对称图形认知的难点。如果直接放手让学生折一折、剪一剪来理解轴对称图形，学生不易办到。学生操作前我先拿一张长方形纸示范操作，请学生观察老师是怎样对折的，再把对折后的纸展开，让学生观察折痕所在的位置，使学生明确，折痕将这张长方形纸分成了大小相等、形状相同的两部分，接着沿刚才的折痕对折，引导学生观察得出这两部份折后完全重合在一起。这样学生既学会了对折，又理解了完全重合。低年级学生通过观察老师的操作，掌握操作过程和方法，为学生的模仿操作创造了条件。

二、指导学生操作，丰富学生的感性认识。

心理学家皮亚杰指出：“活动是认识的基础，智慧从动手开始。”动手操作过程是知识学习的一种循序渐进地探究过程，尤其是小学生的思维是以具体形象思维为主，动手操作便是一种以“动”促“思”，调动多种感官参与学习活动的重要途径。这不仅可以激发学生的学习兴趣，还能帮助学生积累丰富的感性经验，获得鲜明深刻的表象，为学生的理性认识奠定基础。

在教学三角形内角和定理时，首先让学生尝试自学课本，了解操作目的、方法和步骤，再让学生思考：怎样把三角形的三个内角拼在一起？三角形按角分有几种三角形？学生思考后，再指导学生分别把锐角三角形、直角三角形、钝角三角形的三个内角剪（折）拼在一起，观察得出三角形的三个内角拼成了一个平角。学生在头脑中形成了这些三角形的内角和都是180°的鲜明表象。这样三角形的内角和就被演绎在剪与拼的动作里，学生的感性认识上升到理性认识。

三、引导学生在操作中观察、比较，发展学生思维。

观察是人类获取各种知识，养成探求科学真理所发展过程中不可缺少的一步，没有观察就难以比较，没有比较就不能进行深入思考、正确思维；没有比较就不能正确认识各部分及各个特征间的关系，也不能确定各部分知识的异同；更不能找到相关知识间的联系和发展规律。只有把观察、比较贯穿在数学教学的始终，才能让学生在学习过程中有所发现，思维得到发展。

在教学平行四边形的面积公式推导时，为了让学生理解平行四边形与拼成的长方形的各部分间关系，先让学生观察，沿平行四边形的一条高线剪开，得到一个直角三角形和一个直角梯形，即平行四边形的面积就是这两个图形的面积之和，而我们拼成的长方形面积也是这两个图形的面积之和，就得到平行四边形的面积等于拼成的长方形面积。在拼长方形的过程中，引导学生观察和思考：沿平行四边形的高线剪开时，平行四边形的底被分成了两部分，这两部分拼成了长方形的长还是宽？学生动手操作中发现：平行四边形的底就变成了长方形的长，平行四边形的高变成了长方形的宽。学生在操作中观察、比较，获得的平行四边形与拼成的长方形各部分关系的表象是鲜明的，学生的思维也得到发展。

四、在操作过程中，培养学生的创新意识。

在图形知识的教学中，教师除了培养学生动手实践，亲身经历新知识的形成过程外，还应在操作中培养学生的创新意识。教师应鼓励和启发学生对同一问题探索不同的解决方法，只要学生的思路正确，就应给予肯定，以便点燃学生创新思维的火花。

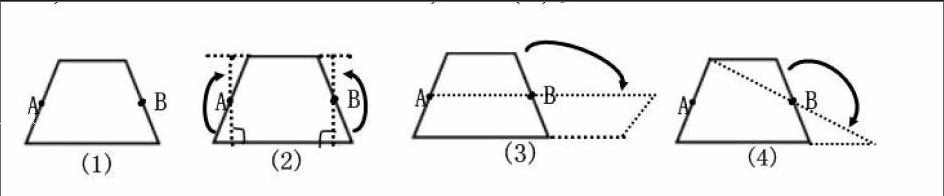
在教学梯形面积时，学生自学课本，都能用两个完全一样的梯形拼成一个平行四边形，根据平行四边形的面积公式推导出梯形的面积计算公式。学生展示自学成果后，我会问：“你们还有别的拼法吗？”我们在推导平行四边形面积公式时用“割补法”，将平行四边形剪拼成长方形。这时用多媒体导出一个梯形，并标出梯形两腰上的中点，如图（1）。过这两个点分别向下底作高，再将这两条高和梯形的上底分别延长，这两条高的延长线和梯形上底的延长线相交，如图（2）。然后让学生分组讨论：能否用“割补法”把梯形剪拼成长方形呢？学生在图（2）的提示下，小组合作探究中，通过观察、动手操作，将梯形剪拼成了长方形。接着又问：“同学们，你们还能把梯形剪拼成我们已经学过的其他图形吗？”这时，我又导入图（1），有的学生马上联想到把梯形两腰中点连接起来，再沿着这条线剪开，将原来的梯形分成了两个梯形，这两个梯形拼成了一个平行四边形，如图（3）。还有的小组将梯形上底的一个顶点和另一条腰上的中点连接，这条连线把原来的梯形分成了一个四边形和一个三角形，剪开后拼成一个大三角形，如图（4）。

通过动手、动脑，合作探究，学生运用不同的方法推导出了梯形面积的计算公式。在“连一连、剪一剪、拼一拼”的实践中，学生的逻辑思维得到了发展，求异创新思维得到了培养。前苏联教育学家苏霍姆林斯基说：“手和脑之间有着千丝万缕的联系，手使脑得到发展，使它变成思维的工具和镜子。”

教学实践证明，在小学数学图形知识的教学中，教具演示和学具操作是符合学生的心理特征和认知规律的。由具体操作思维到形象思维，再由形象思维到抽象思维的发展过程，不但可以激发学生的学习兴趣，由感性认识到理性认识，而且有利于发展学生的逻辑思维，同时还可以点燃学生求异创新思维的火花。

参考文献：

[1]教育部基础教育司组织编写，《走进新课程——与课程实施者对话》，北京师范大出版社，2002年。

[2]中华人民共和国教育部，《义务教育数学课程标准（2011版）》，北京师范大学出版社，2012年。