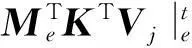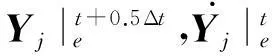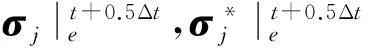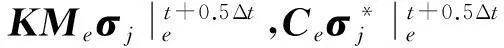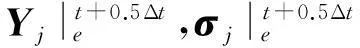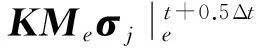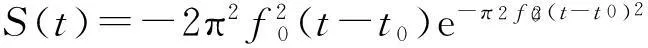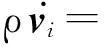一种求解地震波方程的高效并行谱元格式
2016-06-16张林波
林 灯 崔 涛 冷 伟 张林波
(中国科学院数学与系统科学研究院 北京 100190)(科学与工程计算国家重点实验室(中国科学院数学与系统科学研究院) 北京 100190)(lind@lsec.cc.ac.cn)
一种求解地震波方程的高效并行谱元格式
林灯崔涛冷伟张林波
(中国科学院数学与系统科学研究院北京100190)(科学与工程计算国家重点实验室(中国科学院数学与系统科学研究院)北京100190)(lind@lsec.cc.ac.cn)
摘要地震波数值模拟在地震学和地震勘探中扮演着非常重要角色.在已有工作的基础上,提出1种高效并行的地震波PML方程谱元格式.PML被引入地震波方程以吸收外向波进而模拟无界区域.进一步,为了适应复杂地形同时允许时间显式推进,谱元方法被用来离散地震波PML方程.由此得到地震波PML方程谱元格式.在此基础上,阐述了单元刚度矩阵分解性质,并说明了利用单元刚度矩阵分解可以大幅减少刚度矩阵存储量同时显著加速刚度矩阵与向量乘积,进而显著减少格式的计算量和存储量.此外,算法复杂性分析表明格式无论在计算量上还是在存储量上都优于几种已知的1阶地震波PML方程谱元格式.结合并行技术,给出了高效并行的地震波PML方程谱元格式.数值实验验证了格式的正确性、良好的强弱并行可扩展性以及对复杂地形的适应性.
关键词地震波方程;数值模拟;完美匹配层;谱元方法;单元刚度矩阵分解;并行计算
谱元方法(spectral element method, SEM)最初应用于计算流体力学[1-2],随后被成功引入地震波数值模拟领域.其中,Legendre谱元方法离散产生对角质量矩阵,使得时域地震波数值模拟得以显式推进,显著减少了计算开销;同时,谱元方法的高精度、低频散、优良并行性能、适应复杂地形等优势也得以充分展现[3-7].近年来,谱元方法被广泛应用于全球尺度的地震模拟[8-14]及地区尺度的地震模拟[15-18].
速度-应力(应变)格式是地震波数值模拟的常用格式.使用速度-应力(应变)格式可以便捷地结合完美匹配层(perfectly matched layer, PML)[19-20].PML是1种吸收边界层,用以在地震波数值模拟中吸收外向波,模拟无界区域.PML具有2个重要性质:1)波场振幅在PML中指数衰减;2)在离散前对任意入射角及任意频率都有反射系数为零[21].凭借着良好的吸收效果,PML得到了极大的发展和广泛的应用[22-25],也应运而生了许多变种及改进[19-20,22,26-30].
本文基于地震波方程速度-应变-应力形式,应用PML变换及谱元离散,得到地震波PML方程谱元格式.进一步,提出利用单元刚度矩阵分解策略优化刚度矩阵(转置)与向量乘积,有效减少了格式的计算量与存储量.
1地震波方程与PML方法
1.1地震波方程
地震波方程刻画了地震波在地层中传播的基本规律,是地震波数值模拟的基础,在天然地震学及地震勘探等领域扮演着重要的角色.
遵循文献[31],在线性、无粘及理想弹性假设下,地震波方程可写成一阶(时间)系统:
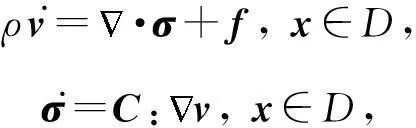
(1)
其中,v是速度,σ是应力张量(2阶对称张量),f为震源(外力),ρ为密度,C是弹性张量(4阶张量).在各向同性假设下,弹性张量可以表写为
Cijkl=λδijδkl+μ(δikδjl+δilδjk),
(2)
其中λ,μ是Lame常数,
借鉴文献[19],将一阶(时间)系统改写成分量形式:
(3)
其中,x∈D,
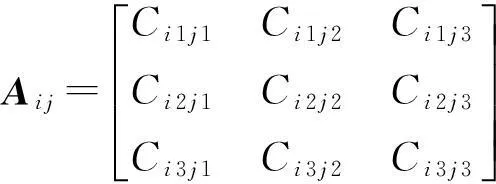
为了确保方程适定性,为1阶(时间)系统附加初值条件:
(4)
其中,x∈D,同时为其附加自由边界条件(也称零载荷边界条件):
σ(x,t)n(x)=0, x∈∂D.
(5)
1.2PML方法
PML方法是目前最为有效的吸收边界层方法.在地震波数值模拟中,PML方法常用于吸收外向波,模拟无穷远边界条件,进而将无界问题转化为有界问题求解.
PML可以解释为复坐标拉伸变换[22]:
(6)
等价微分形式为
(7)
亦即:
(8)
这里i为虚数单位,ω为频率,τk在非PML区域恒为0,在PML区域定义为[32]
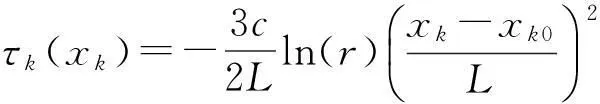
(9)
其中,L为PML厚度,c为最快波速,r为理论反射系数,xk0为沿xk正负方向PML起始坐标.计算区域D由PML区域Dm和非PML区域Dn m构成,如图1所示:

Fig. 1 Components of computational domain.图1 计算区域组成
1.3地震波PML方程
我们把PML方法应用于地震波方程,导出地震波PML方程.
遵循文献[19],对式(3)进行Fourier变换及复坐标拉伸变换,有:
(10)
其中,x∈Dm.引入辅助变量:
(11)
其中:
T≡diag{τ1,τ2,τ3},
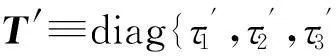
从而有:

(12)
这里e=(1,1,1)T,进而有:
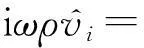
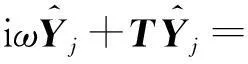
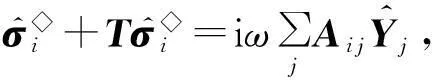
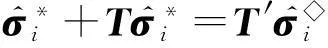
(13)
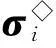
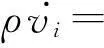
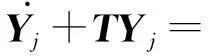
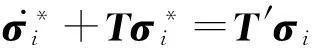
(14)
其中,x∈Dm.值得注意的是,式(14)在非PML区域退化为式(3).
2地震波PML方程谱元格式
2.1谱元离散
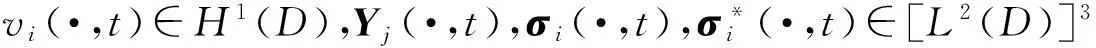
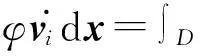
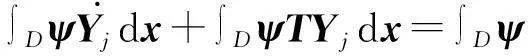
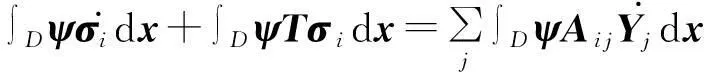
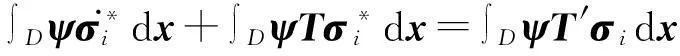
(15)
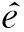
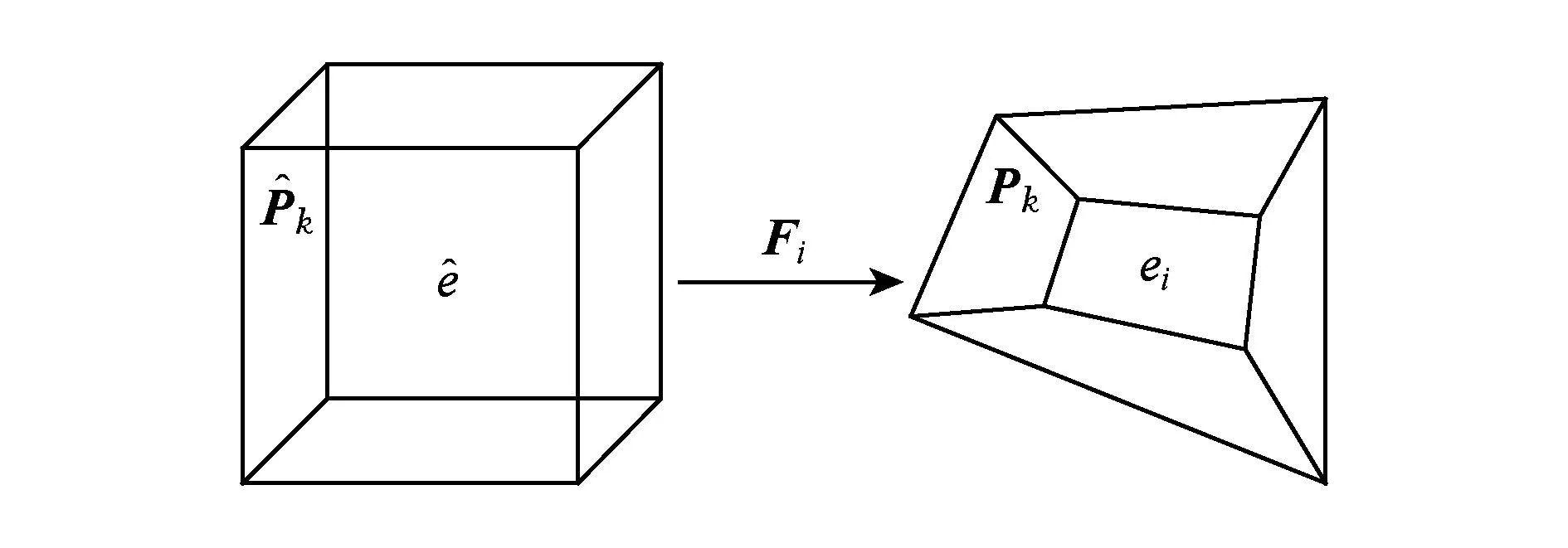
Fig. 2 Invertible map Fi.图2 可逆映射Fi
定义Ji为Fi的Jacobian矩阵,Ji为Ji的行列式,速度场有限元空间Vr定义为
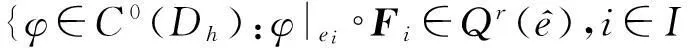
(16)
应力场有限元空间Σr定义为[20]
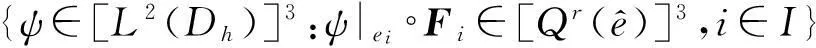
(17)
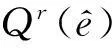
(18)
进一步,通过张量积定义:
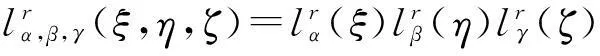
(19)
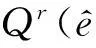
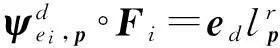
其中,p=(p1,p2,p3),pi=0,1,…,r;ed为第d个分量为1的单位向量.Vr的基函数满足:
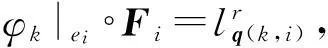
其中,q(k,i)表示q依赖于k及i.在此基础上,对变分形式进行有限元离散,有:
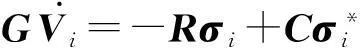
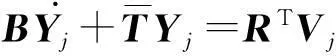
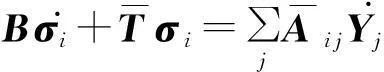
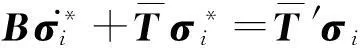
(20)
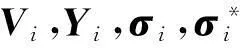
注意到一方面自由度定义在Gauss-Lobatto点,另一方面采用Gauss-Lobatto数值积分公式近似积分,我们有结论:
1) G是对角矩阵.
2) B是对角矩阵,且满足:
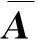
其中,X=Aij,T,T′.
4) Rσi与RTVj可以写为
Rσi=(Reσi|e)e→g,
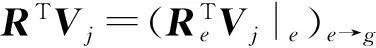

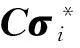
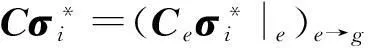
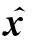
综上所述,我们得到地震波PML方程谱元格式(自由度形式):
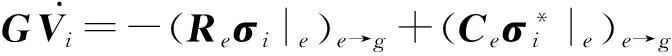
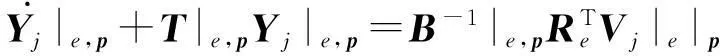
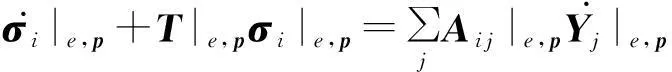
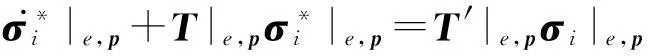
(21)
2.2格式优化
式(21)的计算量高度集中于矩阵(转置)乘向量Rσi与RTVj,存储量主要集中于矩阵R.也就是说,如果格式该部分的计算量和存储量大幅减少,格式整体的计算量和存储量就会显著减少.通过单元刚度矩阵分解优化式(21),注意到单元刚度矩阵具有矩阵分解:
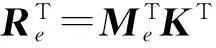
(22)
其中:
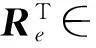
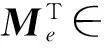
KT∈3n×n,


利用单元刚度矩阵分解计算刚度矩阵(转置)与向量乘积可以简洁表达为
(23)
以下我们说明,利用单元刚度矩阵分解计算刚度矩阵(转置)与向量乘积,无论在存储量上还是在计算量上,都显著优于直接计算刚度矩阵(转置)与向量乘积.


基于地震波PML方程谱元格式,结合单元刚度矩阵分解优化策略,我们得到:
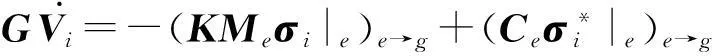
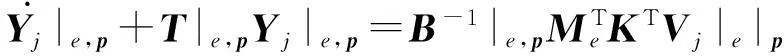
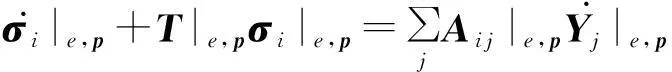

(24)
需要指出的是,我们可以通过变量替换进一步消去质量矩阵B,使得计算量和存储量进一步略微减少.
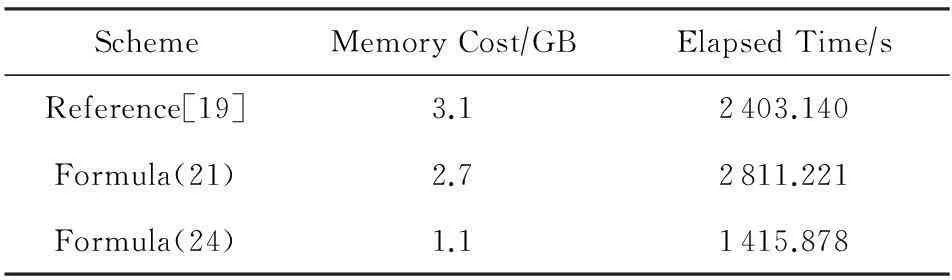
以下是3种地震波PML方程谱元格式在3维非结构网格下内存开销和单个时间步计算量比较.可以看到,无论在计算量还是存储量上,式(24)都显著优于其他2种格式.

Table 1 Storage and Calculation of Spectral Element Schemes for 3D Seismic Wave Equation with PML
Notes:nais the number of PML cells;nogives the amount of non-PML cells;ncis the size of Vi, which satisfiesnc<(r+1)3(na+no).
2.3格式并行化
基于区域分解及消息传递技术[33],我们给出式(24)并行算法.
算法1. 式(24)并行算法.
将网格划分成若干子网格分发到各进程上;将震源及接收点分发给所在进程;计算K,遍历单元计算Me、组装计算G、计算Ce,T,T′等(仅限PML单元).
t=0;
Whilet For All Elements If (PML elements) Else End If End For All Elements 将非本地自由度数据发送给邻居进程; 计算Vj; 从邻居进程获取非本地自由度数据; t=t+Δt; End While 由于该并行算法的计算量与自由度个数成线性关系且MPI通信仅涉及邻居进程,因此该并行算法具有良好的并行可扩展性. 3数值实验 本节算例均在中国科学院数学与系统科学研究院科学和工程计算国家重点实验室LSSC-Ⅲ机群上测试.LSSC-Ⅲ机群拥有282个计算刀片,每个刀片包含2颗Intel X5550处理器和24 GB内存,单核双精度浮点峰值性能为10.68GFLOPS,282个计算结点的总浮点峰值性能为24.09GFLOPS.所有结点通过DDR Infiniband网络互联.程序部分依赖于3维并行自适应有限元平台PHG[34]. 在地震波数值模拟中,必须约束时空采样以抑制时空频散.遵循文献[35],程序采用8阶谱元作空间离散并让空间采样不低于每个最短波长5个采样点,同时采用2阶leapfrog格式作时间离散并让时间采样不低于每个最短周期12个采样点.注意到式(24)是显格式,空间步长与时间步长还受CFL条件约束[36]. 3.1验证格式正确性 本节通过解析解与数值解的比较验证式(24)的正确性.考虑2维算例如图3所示.每个方向64个单元,共4 096个单元.时间步长为0.4×10-3,推进步数为5 000.采用P波震源如下: 其中,δ是delta函数,I为单位矩阵, Fig. 3 Specification of the 2D benchmark.图3 2维算例设定 震源主频f0=10 Hz,震源时移t0=0.12 s,震源位于(0,0.375),比例因子m=1.接收点位于(0.61,-0.61).PML厚度为0.25,理论反射系数为0.000 1.计算结果如图4、图5所示.图4给出了0.6 s时刻速度场垂直分量快照. 其中,透射P波(a)、透射P-to-S波(b)、反射P-to-S波(c)、反射P波(d)及直达P波(e)清晰可见.图5给出了速度场垂直分量在接收点(0.61,-0.61)处的解析解及数值解.解析解由Gar6more2D[37]计算得到,可以看到,解析解与数值解吻合得很好. Fig. 4 Snapshot of vertical component of velocity field at 0.6 s.图4 0.6 s时刻速度场垂直分量快照 Fig. 5 Comparison between the analytic and numerical solutions of vertical component of velocity field at the receiver.图5 速度场竖直分量在接收点处解析解与数值解比较 3.2验证格式性能优势 本节通过比较在同一数值算例下3种地震波PML方程谱元格式的内存开销和计算时间验证式(24)的性能优势.考虑模型问题如下:计算区域为[-0.5,0.5]3,每个方向16个单元,共4 096个单元.时间步长为0.75×10-3,推进步数为1 000.采用速度震源如下: 其中,δ及S的定义见3.1节.震源主频f0=10 Hz,震源时移t0=0.12 s,震源位于区域中心,比例因子m为1.区域为单一均匀介质,介质密度为1,P波速度为1.732,S波速度为1.PML厚度为0.25,理论反射系数为0.000 1.表2比较了3种地震波PML方程谱元格式的内存开销和计算时间.从表2可以看出,式(24)确实在计算量和存储量上显著优于其他2种格式. Table 2 Performance of Spectral Element Schemes for 3.3格式弱可扩展性测试 本节对式(24)进行弱可扩展性测试.考虑模型问题如下:网格单元均为边长为0.062 5的立方体,时间步长为0.000 75,推进步数为1 000.震源形式与3.2节相同,震源主频f0=10 Hz,震源时移t0=0.12 s,震源位于区域中心,比例因子为1.区域为单一均匀介质,介质密度为1,P波速度为1.732,S波速度为1,不设置PML,网格规模随进程数变化而变化,确保每个进程所拥有的网格单元个数近似相等,从而,每个进程所拥有的自由度个数大体相同.计算结果如表3所示.从表3可以看出,式(24)具有良好的弱可扩展性. Table 3 Weak Scalability Test of Formula(24) 3.4格式强可扩展性测试 本节对式(24)进行强可扩展性测试.考虑模型问题如下:计算区域为[-2,2]3,每个方向加密6次,共有262 144个单元,谱元阶数为8,时间步长为0.000 75,推进步数为1 000.震源设定及介质设定均与3.2节相同.速度分量自由度个数为135 005 697,应力分量自由度个数为573 308 928.表4给出了采用不同进程数进行计算的推进用时及并行效率.这里,并行效率定义为 其中,s是参与计算的进程数.之所以与16个进程的计算结果比较是由于算例内存开销较大.从表4可以看出,式(24)具有良好的强可扩展性. Table 4 Strong Scalability Test of Formula(24) Fig. 6 Computational domain and its unstructured hexahedral mesh图6 计算区域及其非结构六面体网格 3.5起伏地表 式(24)能够有效模拟地震波在实际地形中传播.考虑计算问题如下:计算区域为30.91°N~31.11°N,103.32°E~103.52°E,地下深度12.5 km.Digital Elevation Model数据来源于Shuttle Radar Topographic Mission,如图6所示.时间步长Δt=0.002 s,时间步数为4 000.震源形式与3.2节相同.震源主频f0=2 Hz,震源时移t0=0.6 s,震源位于31.01°N,103.42°E,震源深度为8 km,比例因子m=108.区域为单一均匀介质,密度ρ=3.0 gcm3,P波速度为3.5 kms,S波速度为2.02 kms.PML厚度L=2.5 km,理论反射系数r=0.000 1.速度分量自由度个数为26 651 025,应力分量自由度个数为37 558 080.图7显示了4.8 s时刻速度竖直分量波场图. Fig. 7 Snapshot of vertical component of velocity field at 4.8 s.图7 4.8 s时刻速度场竖直分量快照 4结束语 本文从地震波方程速度-应变-应力形式出发,应用PML方法导出地震波PML方程.进一步,应用谱元方法得到地震波PML方程谱元格式.在此基础上,提出利用单元刚度矩阵分解优化刚度矩阵(转置)与向量乘积,避免了刚度矩阵存储,有效减少了格式的计算量与存储量.数值实验验证了该格式的正确性、性能优势及良好的并行强弱可扩展性,并把该格式应用于实际地形中.下一步我们将结合Local Time Stepping技术把该格式应用于真实的大规模的地震波数值模拟. 参考文献 [1]Patera A T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion[J]. Journal of Computational Physics, 1984, 54(3): 468-488 [2]Maday Y, Patera A T. Spectral element methods for the incompressible Navier-Stokes equations[C]Proc of State-of-the-Art Surveys on Computational Mechanics. New York: ASME, 1989: 71-143 [3]Cohen G, Joly P, Tordjman N. Construction and analysis of higher-order finite elements with mass lumping for the wave equation[C]Proc of the 2nd Int Conf on Mathematical and Numerical Aspects of Wave Propagation. Philadelphia, PA: SIAM, 1993: 152-160 [4]Faccioli E, Maggio F, Paolucci R, et al. 2D and 3D elastic wave propagation by a pseudo- spectral domain decomposition method[J]. Journal of Seismology, 1997, 1(3): 237-251 [5]Komatitsch D. Spectral and spectral element methods for the 2D and 3D elastodynamics equations in heterogeneous media[D]. Paris: The Institute of Earth Physics of Paris, 1997 [6]Komatitsch D, Vilotte J P. The spectral element method: An efficient tool to simulate the seismic response of 2D and 3D geological structures[J]. Bulletin of the Seismological Society of America, 1998, 88(2): 368-392 [7]Komatitsch D, Tromp J. Introduction to the spectral-element method for 3-D seismic wave propagation[J]. Geophysical Journal International, 1999, 139(3): 806-822 [8]Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation-I: Validation[J]. Geophysical Journal International, 2002, 149(2): 390-412 [9]Komatitsch D, Tromp J. Spectral-element simulations of global seismic wave propagation-Ⅱ: Three-dimensional models, oceans, rotation and self-gravitation[J]. Geophysical Journal International, 2002, 150(1): 303-318 [10]Komatitsch D, Ritsema J, Tromp J. The spectral-element method, Beowulf computing, and global seismology[J]. Science, 2002, 298(5599): 1737-1742 [11]Komatitsch D, Tsuboi S, Ji C, et al. A 14.6 billion degrees of freedom, 5 teraflops, 2.5 terabyte earthquake simulation on the Earth Simulator[C]Proc of the 2003 ACMIEEE Conf on Supercomputing. New York: ACM, 2003 [12]Chaljub E. Numerical modeling of the propagation of seismic waves in spherical geometry: Applications to global seismology[D]. Paris: University of Paris Ⅶ Denis Diderot, 2000 [13]Chaljub E, Capdeville Y, Vilotte J P. Solving elastodynamics in a fluid-solid heterogeneous sphere: A parallel spectral element approximation on non-conforming grids[J]. Journal of Computational Physics, 2003, 187(2): 457-491 [14]Chaljub E, Valette B. Spectral element modelling of three-dimensional wave propagation in a self-gravitating earth with an arbitrarily stratified outer core[J]. Geophysical Journal International, 2004, 158(1): 131-141 [15]Komatitsch D, Liu Q, Tromp J, et al. Simulations of ground motion in the Los Angeles basin based upon the spectral-element method[J]. Bulletin of the Seismological Society of America, 2004, 94(1): 187-206 [16]Liu Q, Polet J, Komatitsch D, et al. Spectral-element moment tensor inversions for earthquakes in southern California[J]. Bulletin of the Seismological Society of America, 2004, 94(5): 1748-1761 [17]Lee S J, Chen H W, Liu Q, et al. Three-dimensional simulations of seismic-wave propagation in the Taipei basin with realistic topography based upon the spectral-element method[J]. Bulletin of the Seismological Society of America, 2008, 98(1): 253-264 [18]Chaljub E, Moczo P, Tsuno S, et al. Quantitative comparison of four numerical predictions of 3D ground motion in the Grenoble Valley, France[J]. Bulletin of the Seismological Society of America, 2010, 100(4): 1427-1455 [19]Cohen G, Fauqueux S. Mixed spectral finite elements for the linear elasticity system in unbounded domains[J]. SIAM Journal on Scientific Computing, 2005, 26(3): 864-884 [20]Festa G, Vilotte J P. The Newmark scheme as velocity-stress time-staggering: An efficient PML implementation for spectral element simulations of elastodynamics[J]. Geophysical Journal International, 2005, 161(3): 789-812 [21]Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200 [22]Chew W C, Weedon W H. A 3D perfectly matched medium from modified Maxwell’s equations with stretched coordinates[J]. Microwave and Optical Technology Letters, 1994, 7(13): 599-604 [23]Chew W C, Liu Q H. Perfectly matched layers for elastodynamics: A new absorbing boundary condition[J]. Journal of Computational Acoustics, 1996, 4(4): 341-359 [24]Liu Q H, Tao J. The perfectly matched layer for acoustic waves in absorptive media[J]. The Journal of the Acoustical Society of America, 1997, 102(4): 2072-2082 [25]Zeng Y Q, He J Q, Liu Q H. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media[J]. Geophysics, 2001, 66(4): 1258-1266 [26]Komatitsch D, Tromp J. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation[J]. Geophysical Journal International, 2003, 154(1): 146-153 [27]Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 2007, 72(5): 155-167 [28]Meza-Fajardo K C, Papageorgiou A S. A nonconvolutional, split-field, perfectly matched layer for wave propagation in isotropic and anisotropic elastic media: Stability analysis[J]. Bulletin of the Seismological Society of America, 2008, 98(4): 1811-1836 [29]Martin R, Komatitsch D, Gedney S D, et al. A high-order time and space formulation of the unsplit perfectly matched layer for the seismic wave equation using auxiliary differential equations (ADE-PML)[J]. Computer Modeling in Engineering and Sciences, 2010, 56(1): 17-42 [30]Chen Z, Cui T, Zhang L. An adaptive anisotropic perfectly matched layer method for 3-D time harmonic electromagnetic scattering problems[J]. Numerische Mathematik, 2013, 125(4): 639-677 [31]Fichtner A. Full Seismic Waveform Modelling and Inversion[M]. Berlin: Spinger, 2010 [32]Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307 [33]Zhang Linbo, Chi Xuebin, Mo Zeyao, et al. An Introduction to Parallel Computing[M]. Beijing: Tsinghua University Press, 2006 (in Chinese)(张林波, 迟学斌, 莫则尧, 等. 并行计算导论[M]. 北京: 清华大学出版社, 2006) [34]Zhang Linbo. Parallel hierarchical grid (PHG)[CPOL]. [2014-07-03]. http:lsec.cc.ac.cnphg [35]Seriani G, Oliveira S P. Dispersion analysis of spectral element methods for elastic wave propagation[J]. Wave Motion, 2008, 45(6): 729-744 [36]Courant R, Friedrichs K, Lewy H. On the partial difference equations of mathematical physics[J]. IBM Journal of Research and Development, 1967, 11(2): 215-234 [37]Diaz J, Ezziani A. Gar6more2D[CPOL]. [2014-05-20]. http:gar6more2d.gforge.inria.fr Lin Deng, born in 1989. PhD candidate in Academy of Mathematics and Systems Science, Chinese Academy of Sciences. His main research interests include parallel computing and seismic exploration. Cui Tao, born in 1979. PhD and associate professor in Academy of Mathematics and Systems Science, Chinese Academy of Sciences. His main research interests include parallel computing and electromagnetic computing. Leng Wei, born in 1984. PhD and assistant professor in Academy of Mathematics and Systems Science, Chinese Academy of Sciences. His main research interests include parallel computing and seismic exploration. Zhang Linbo, born in 1962. Professor and PhD supervisor in Academy of Mathematics and Systems Science, Chinese Academy of Sciences. His main research interests include parallel computing especially 3D parallel (adaptive) finite element computing. An Efficient Parallel Spectral Element Scheme for Solving Seismic Wave Equation Lin Deng, Cui Tao, Leng Wei, and Zhang Linbo (AcademyofMathematicsandSystemSciences,ChineseAcademyofSciences,Beijing100190)(StateKeyLaboratoryofScientificandEngineeringComputing(AcademyofMathematicsandSystemSciences,ChineseAcademyofSciences),Beijing100190) AbstractNumerical simulation of seismic waves plays an essential role in seismology and seismic exploration. We propose here an efficient parallel spectral element scheme for seismic wave equation with perfectly matched layer (PML). PML is integrated into the seismic wave equation to absorb out-going waves and mimic unbounded domain. Ulteriorly, to enable adapting complex topography and explicit time stepping, the spectral element method (SEM) is used to discretize seismic wave equation with PML, which results in a spectral element scheme. In addition, we demonstrate that element stiffness matrices can be decomposed, which can be used to greatly reduce the storage of stiffness matrix and accelerate stiffness matrix-vector multiplication and thus remarkably speed up the scheme and cut down memory cost. Furthermore, we study several spectral element schemes known and show that our scheme is superior to others in both calculation and storage. Combined with parallel technique, an efficient parallel spectral element solver for seismic wave equation with PML is present. Numerical experiments show that our scheme is correct, well strongly�weakly scalable and of good adaptation to complex topography. Key wordsseismic wave equation; numerical simulation; perfectly matched layer (PML); spectral element method (SEM); element stiffness matrices decomposition; parallel computing 收稿日期:2014-12-30;修回日期:2015-04-03 基金项目:国家“九七三”重点基础研究发展计划基金项目(2011CB309703);国家“八六三”高技术研究发展计划基金项目(2012AA01A309);国家自然科学基金项目(11171334,11321061,11101417);中国科学院国家数学与交叉科学中心资助课题 中图法分类号TP391 This work was supported by the National Basic Research Program of China (973 Program) (2011CB309703), the National High Technology Research and Development Program of China (863 Program) (2012AA01A309), the National Natural Science Foundation of China (11171334, 11321061, 11101417), and the Foundation of the National Center for Mathematics and Interdisciplinary Sciences, Chinese Academy of Sciences.