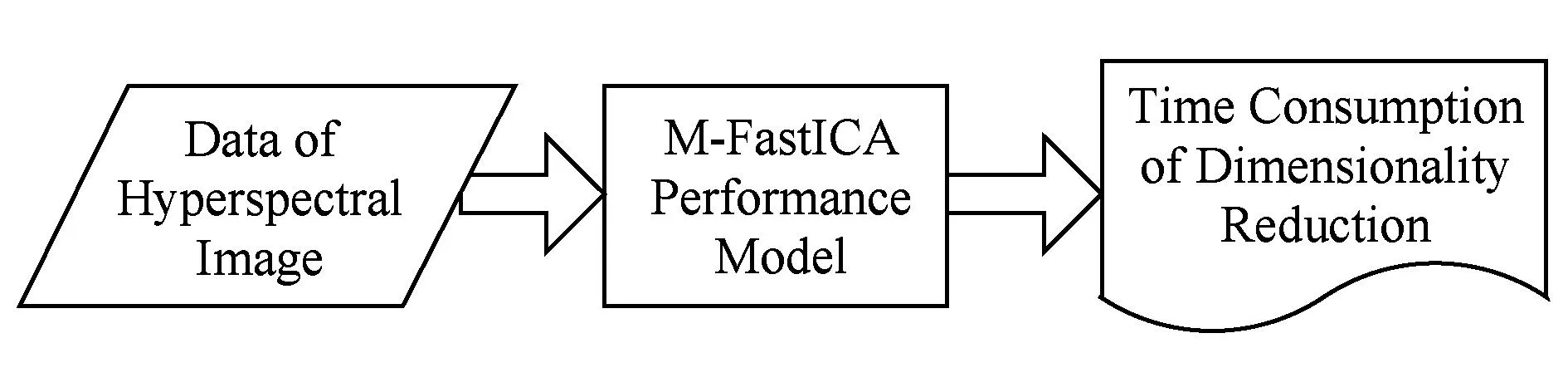
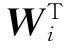集成众核上快速独立成分分析降维并行算法
2016-06-16方民权张卫民周海芳
方民权 张卫民 周海芳
(国防科学技术大学计算机学院 长沙 410073)(fmq@hpc6.com)
集成众核上快速独立成分分析降维并行算法
方民权张卫民周海芳
(国防科学技术大学计算机学院长沙410073)(fmq@hpc6.com)
摘要高光谱遥感影像快速独立成分分析(fast independent component analysis, FastICA)降维过程包含大规模矩阵计算及大量迭代计算.通过热点分析,面向集成众核(many integrated core, MIC)架构设计了协方差矩阵计算、白化处理和ICA迭代等热点并行方案,提出和实现一种M-FastICA并行降维算法,并构建算法性能模型;基于集成众核研究并行程序优化策略,针对各热点并行方案提出一系列优化策略,特别是创新性地提出一种下三角阵负载均衡方法,并量化测试其优化效果.实验结果显示M-FastICA算法最高可加速42倍,比24核CPU多线程并行快2.2倍;探讨了波段数与并行程序性能的关系;实验数据验证了算法性能模型的准确性.
关键词集成众核;独立成分分析;高光谱影像降维;性能模型;下三角阵负载均衡
高光谱遥感技术广泛应用于军事、农业、环境科学、地质、海洋学等领域,这些领域大都要求及时处理[1].但高光谱影像数据有波段多、数据量大、相关性强、冗余多等特点,直接处理将导致样本类别训练困难、维数灾难、空空间现象等严重的计算问题[2-4].因此,国内外专家学者处理高光谱影像数据过程常常包括降维步骤.降维是通过特定的映射,将高维影像数据转换成低维影像数据,并保持信息量基本不变.
高光谱影像降维方法可分为线性和非线性2类,线性降维有主成分分析(principal component analysis, PCA)[5]、独立成分分析(independent component analysis, ICA)[6]等方法;非线性降维包括基于核的方法和基于流行学习的方法,如等距映射法(isometric feature mapping, Isomap)[7]、局部线性嵌入(locally linear embedding, LLE)[8]等.由于高光谱影像波段多、数据量大等特征,降维处理过程复杂且耗时.提高降维速度是重要研究热点,王和勇等人[9]研究基于聚类和改进距离的LLE方法以提高5.5倍降维速度;而并行降维是加快降维过程的另一个重要研究方向.
自Intel公司2012年推出集成众核(many integ-rated core, MIC)产品Phi[10],集成众核已成为目前高性能计算领域的研究热点,搭载MIC的天河2号超级计算机已连续6届登临TOP500榜首[11].
高光谱影像并行处理在传统并行系统已有成熟的应用:Valencia等人[12]基于异构MPI在网络机群系统研究了高光谱影像处理的技术;Plaza等人[13]提出基于神经网络的高光谱影像并行分类算法.基于CPUGPU异构系统,高光谱影像并行处理也有部分研究:Sánchez等人[14]对高光谱解混进行了GPU移植;Platoš等人[15]和Ramalho等人[16]分别用GPU加速了非负矩阵分解和独立成分分析等降维方法.但基于CPU+MIC这一新型高性能体系结构还没有相关研究.本文将面向集成众核架构探讨加速高光谱影像降维的可行性.
本文以基于负熵最大的快速独立成分分析(fast independent component analysis, FastICA)算法[17-18]为对象,面向集成众核架构展开并行算法研究,本文贡献包括:1)分析算法加速热点并设计相应的并行方案;2)针对各热点并行方案提出并验证了多种建设性的优化策略,特别是创新性地提出一种下三角阵负载均衡策略;3)提出并实现了一种并行降维算法M-FastICA;4)设计了该并行算法的性能预测模型,并验证了其有效性.
1集成众核体系结构与优化策略
1.1集成众核体系结构
英特尔集成众核MIC架构集成了超过50个x86核心,由片上高速环形互联总线联接如图1所示.MIC共有8个基于GDDR5的存储控制器、16个通道,峰值带宽可达350 GBps[10].
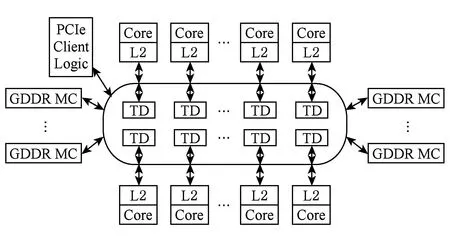
Fig. 1 Many integrated core architecture.图1 MIC架构
MIC的每个计算核心拥有1个512 b的向量处理单元(vector processing unit, VPU)、1个x86架构标量处理单元、32 KB的L1 cache(指令和数据各1个)和512 KB的L2 cache.MIC支持硬件多线程技术,每个核心有4个硬件线程,但发射1条指令需要2个时钟[10].
MIC搭载的嵌入式Linux uOS使其具有5种不同的工作模式:CPU原生模式、CPU为主MIC为辅模式、对等模式、MIC为主CPU为辅模式和MIC原生模式[10].本文使用CPU为主MIC为辅模式.
1.2集成众核优化策略
MIC是众核协处理器,要获得最优性能,可以采取的一般优化策略包括并行度、内存空间、数据通信、Cache访问、向量化、负载均衡、线程扩展性等方面优化.对于CPUMIC异构系统,如何合理分配CPU和MIC的计算任务、如何设计host端和device端的通信这些都是异构系统优化过程中所必须考虑的重要因素.
2独立成分分析算法与加速热点
2.1基于负熵最大的快速独立成分分析
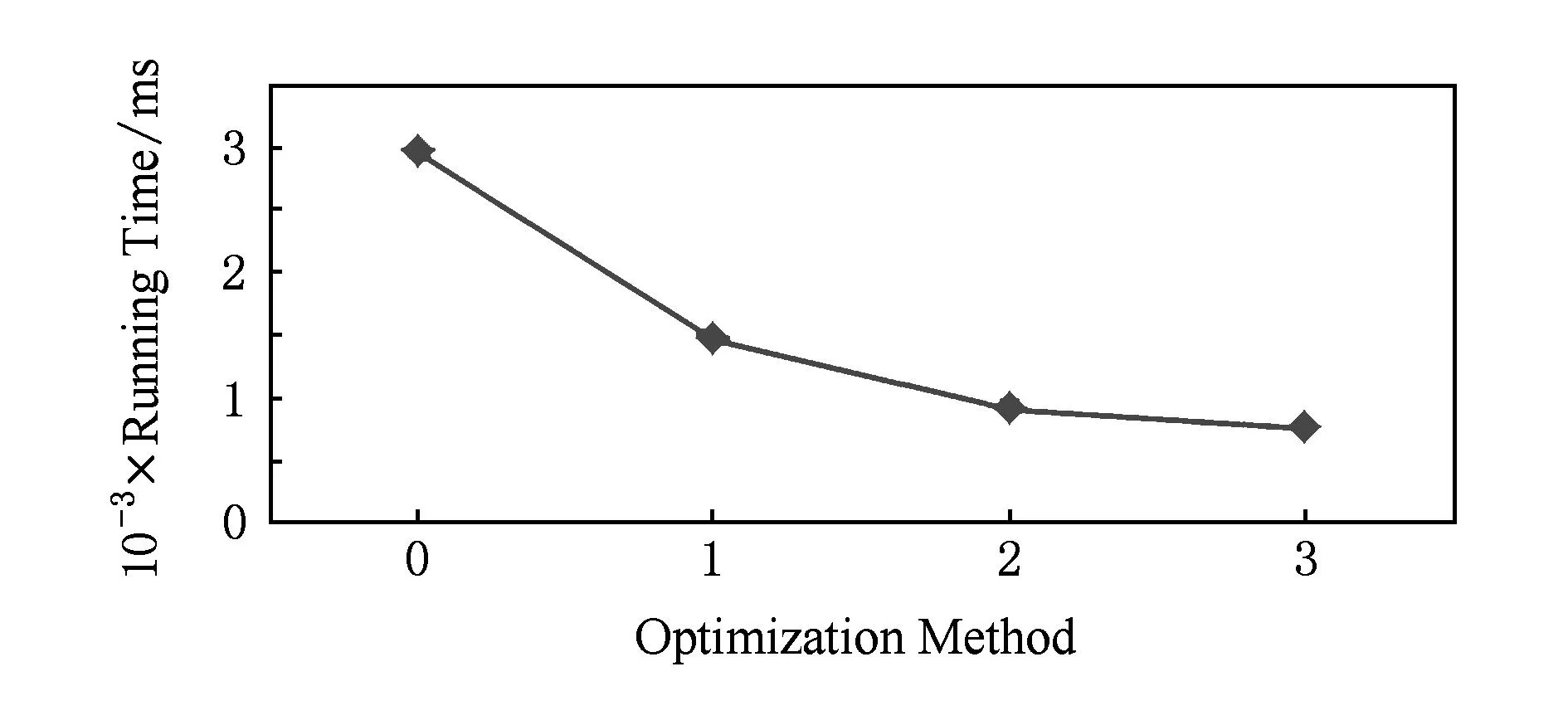
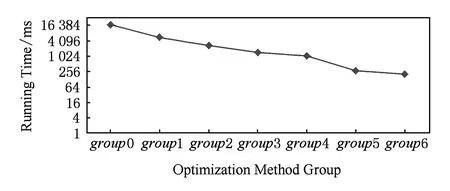
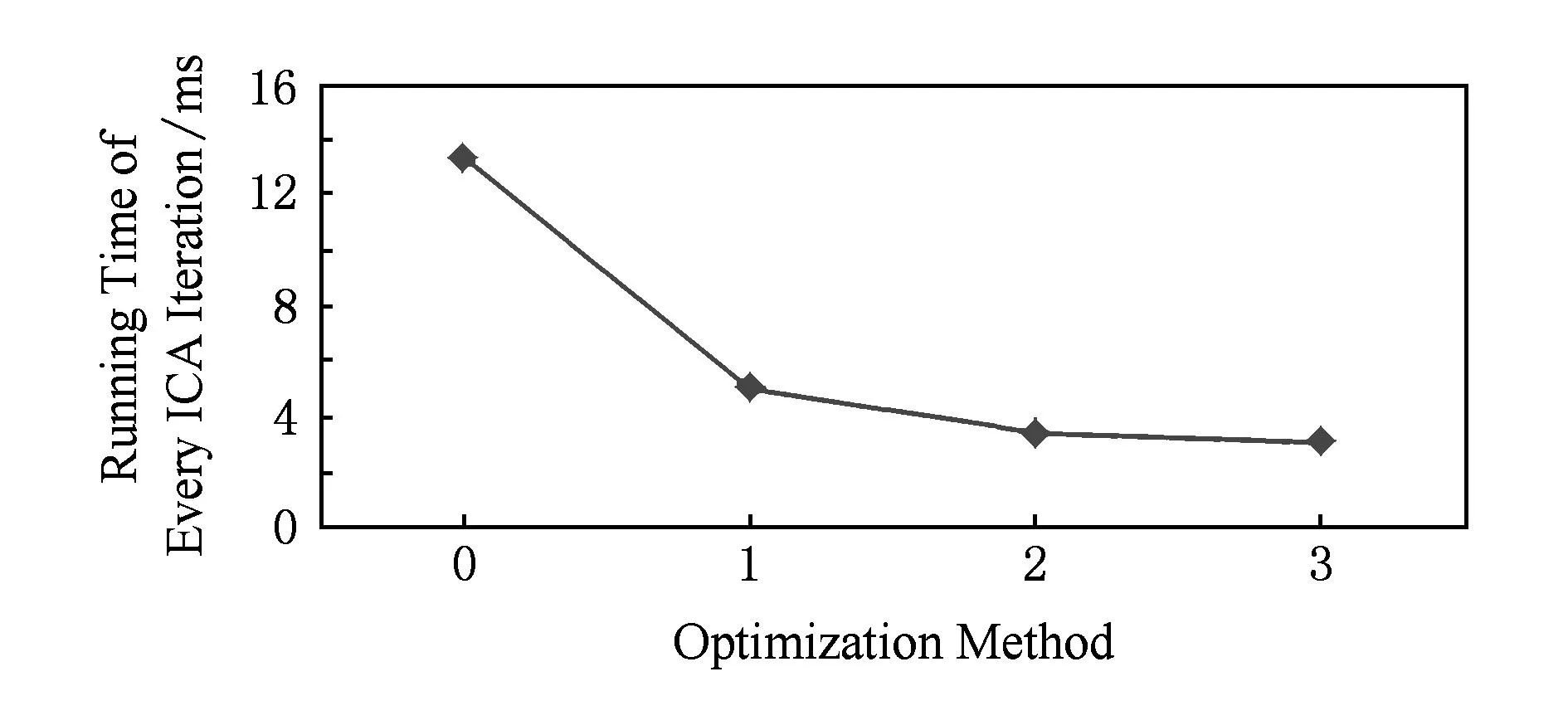
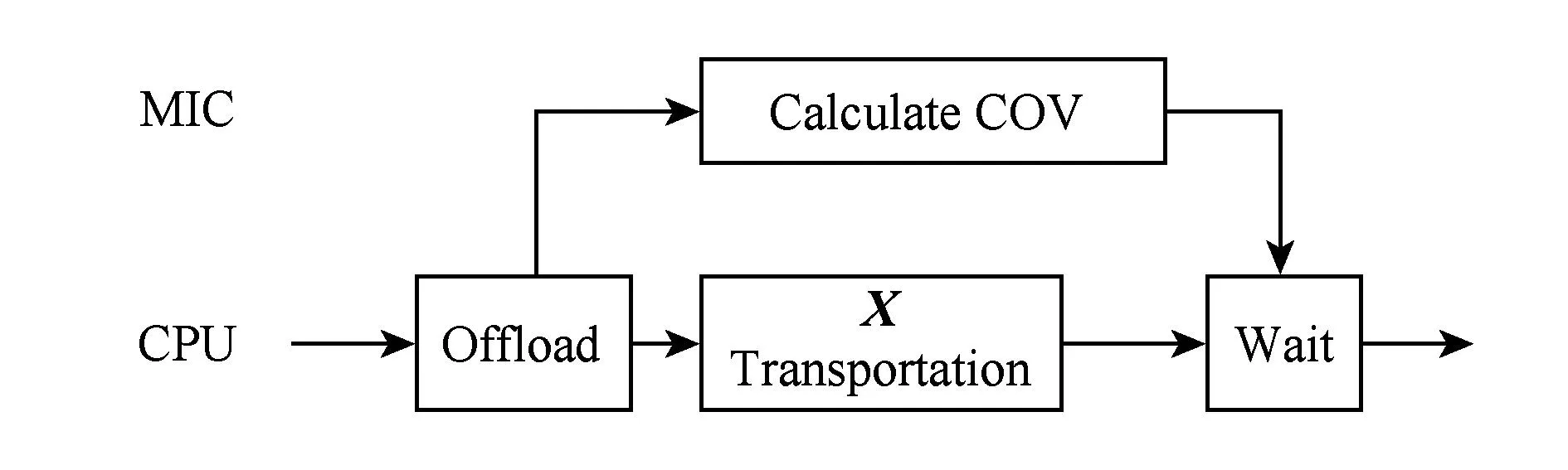
FastICA算法有基于负熵最大、基于似然最大、基于峭度3种形式,本文研究基于负熵最大的FastICA算法.该算法以负熵最大为搜寻方向,实现独立源的顺序提取,充分体现传统线性变换中的投影追踪思想,该算法还采用定点迭代的优化算法,使收敛更加快速、稳健[17-18].
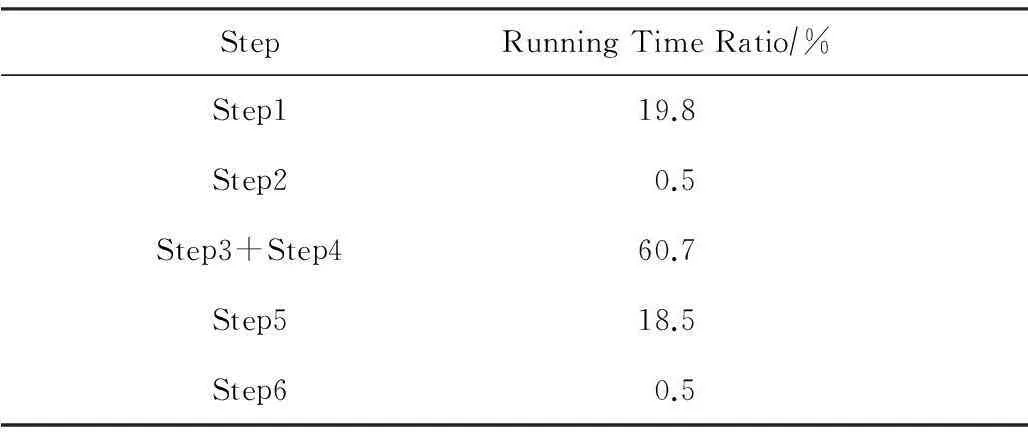
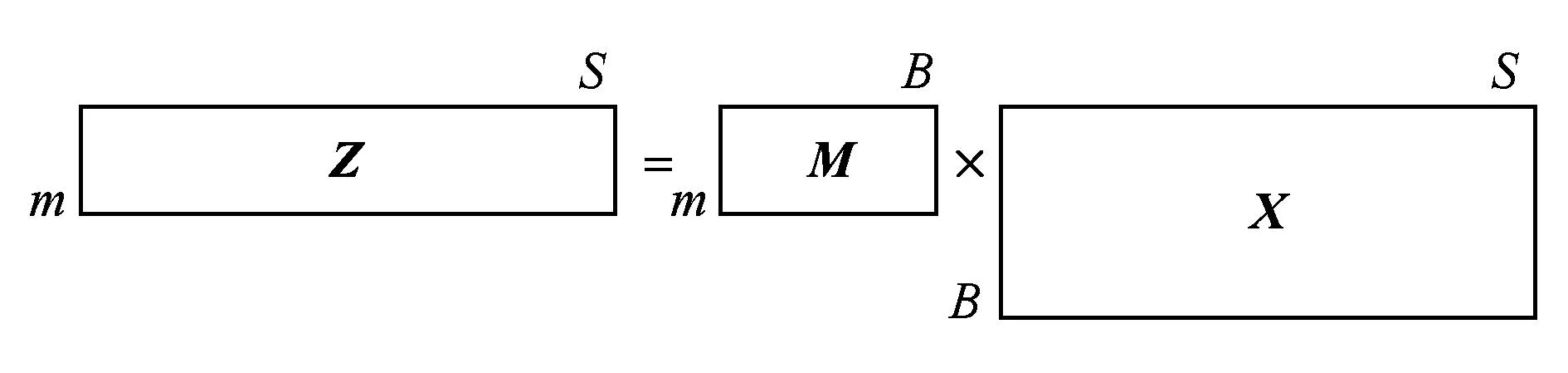
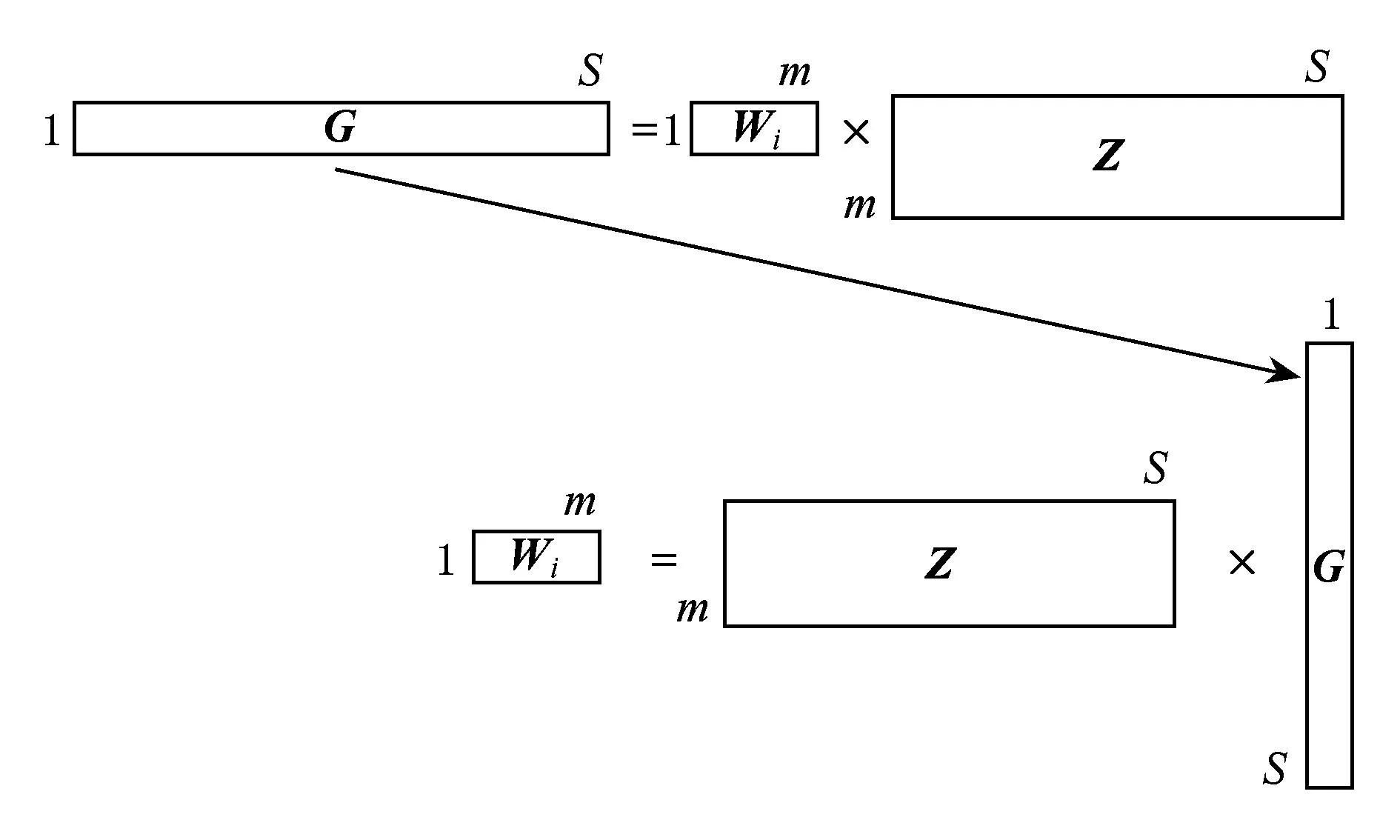
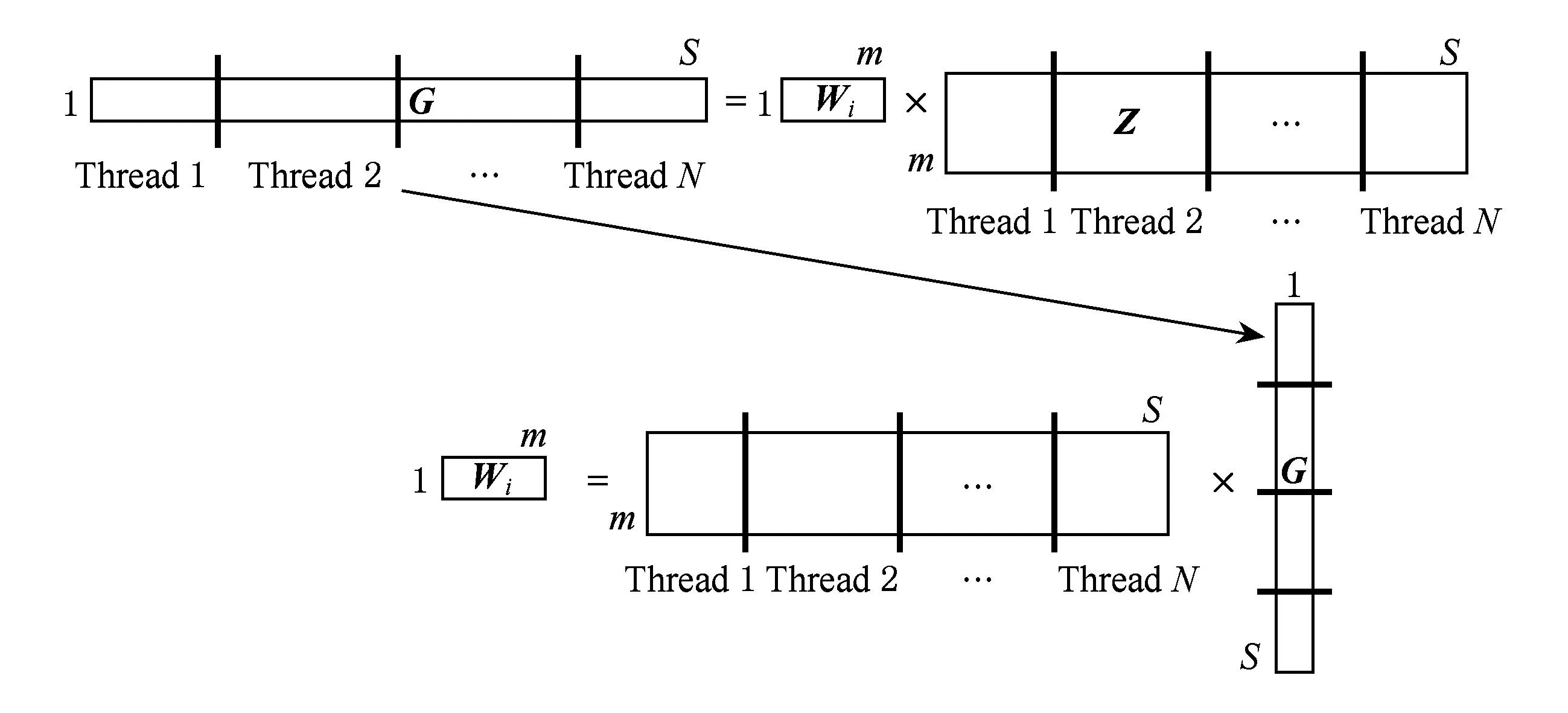
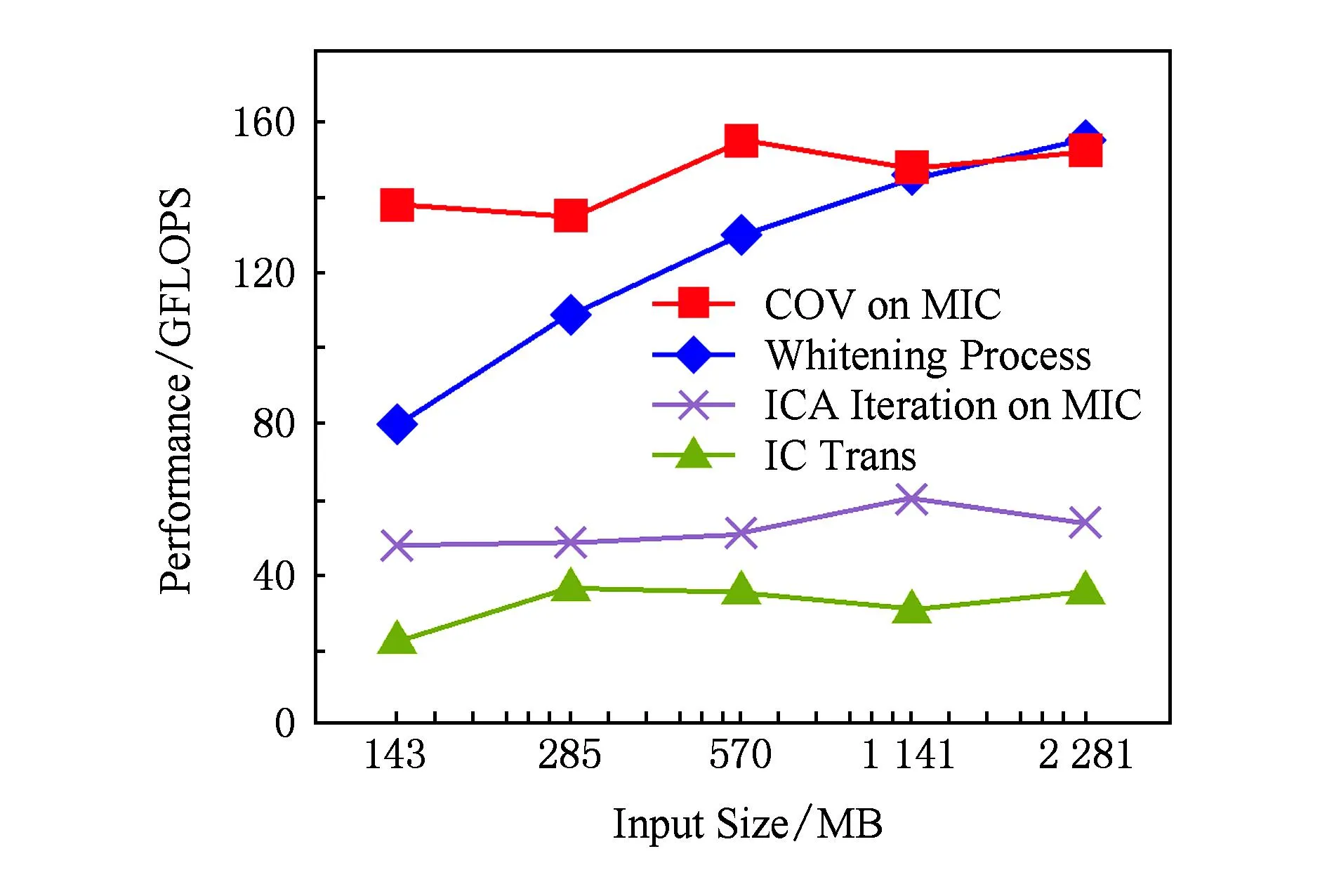
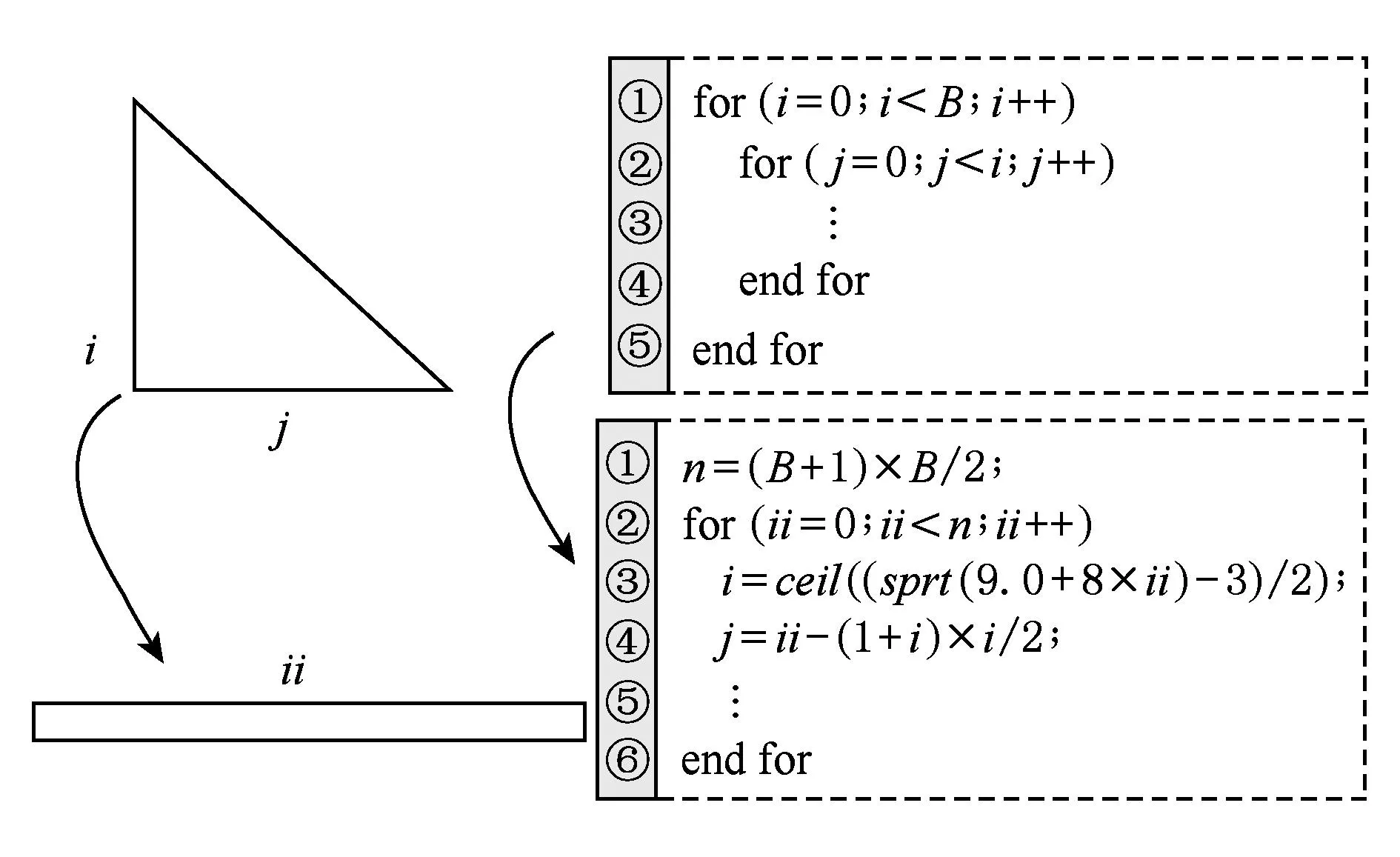
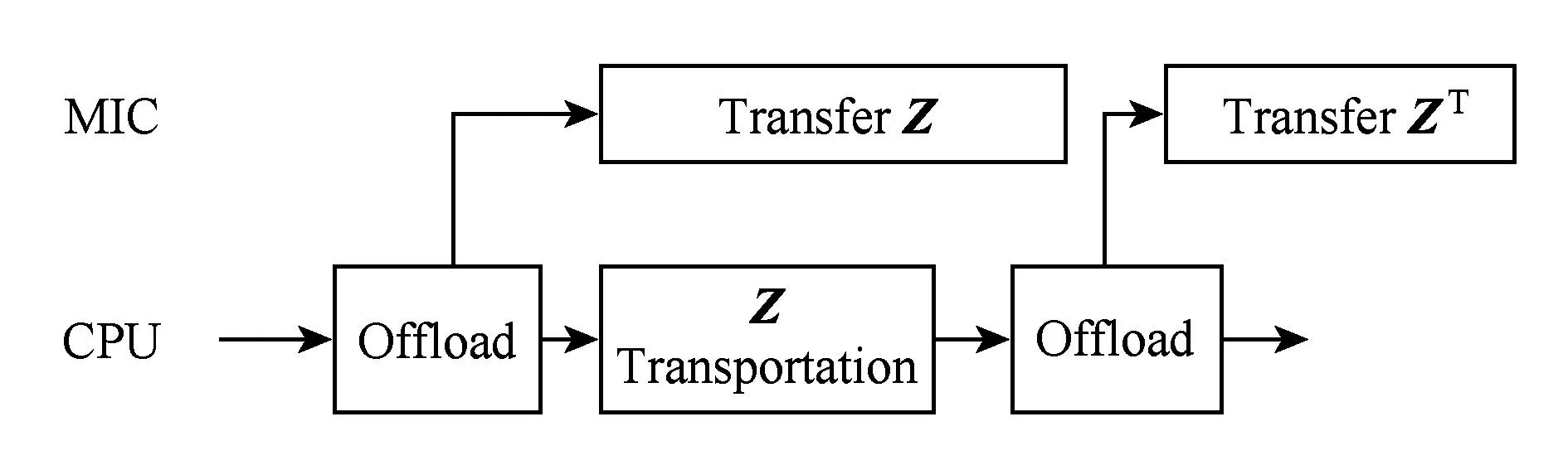
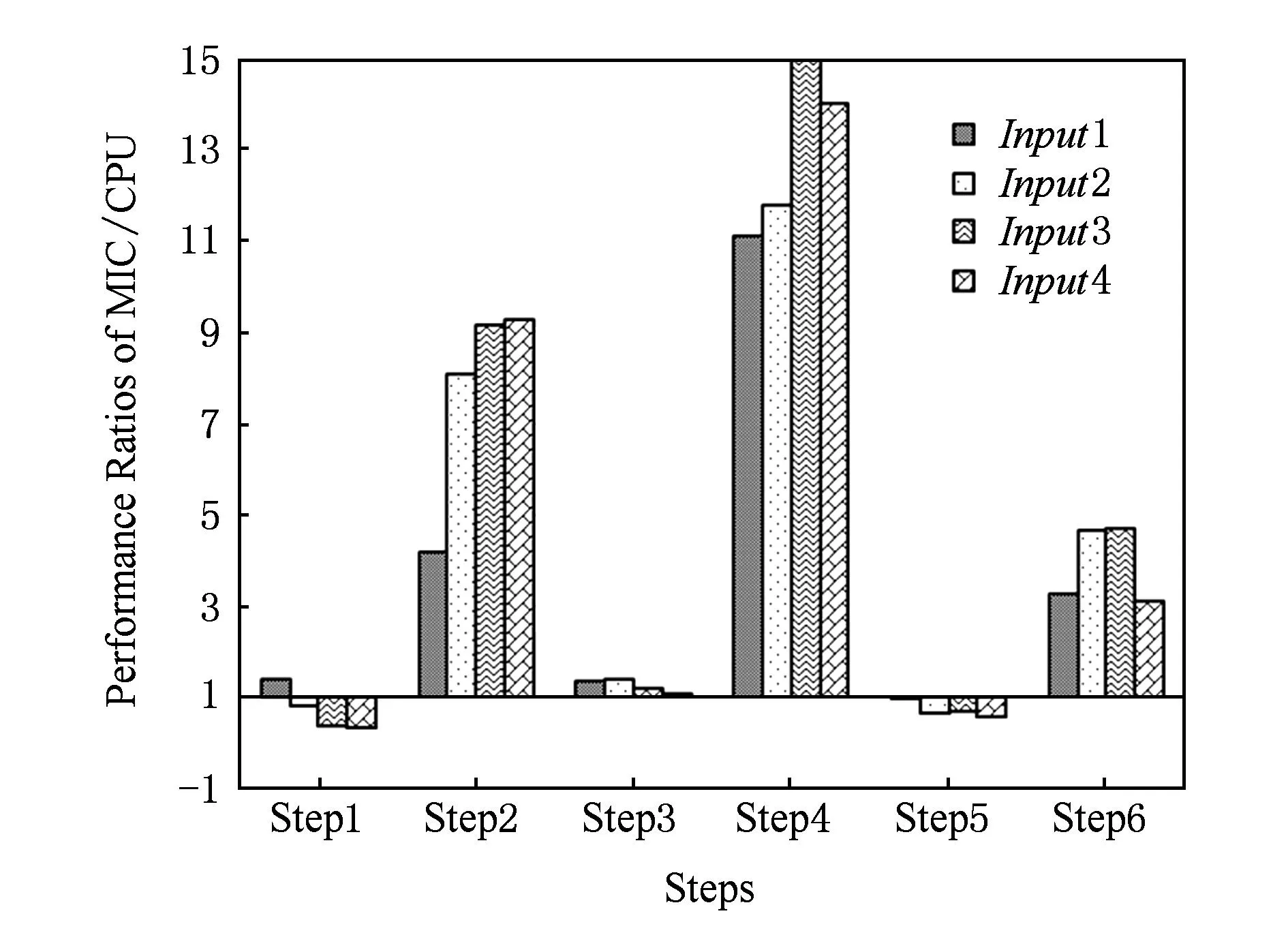
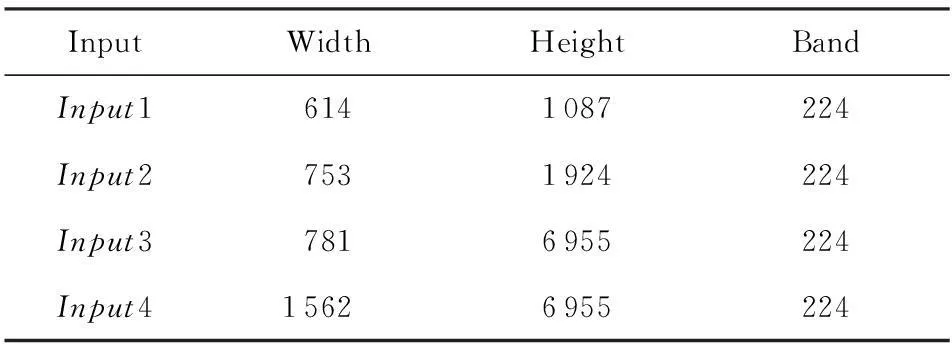
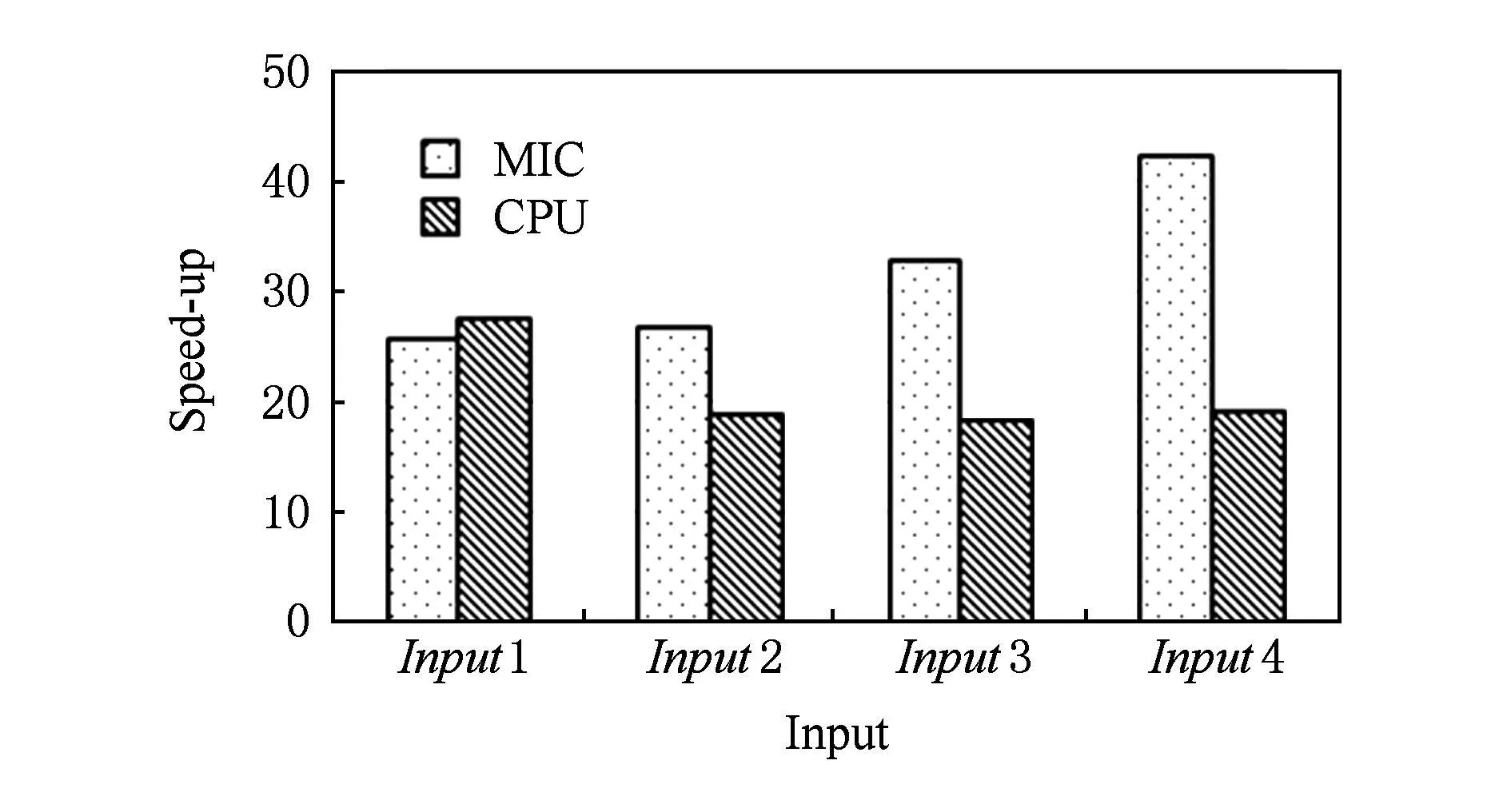
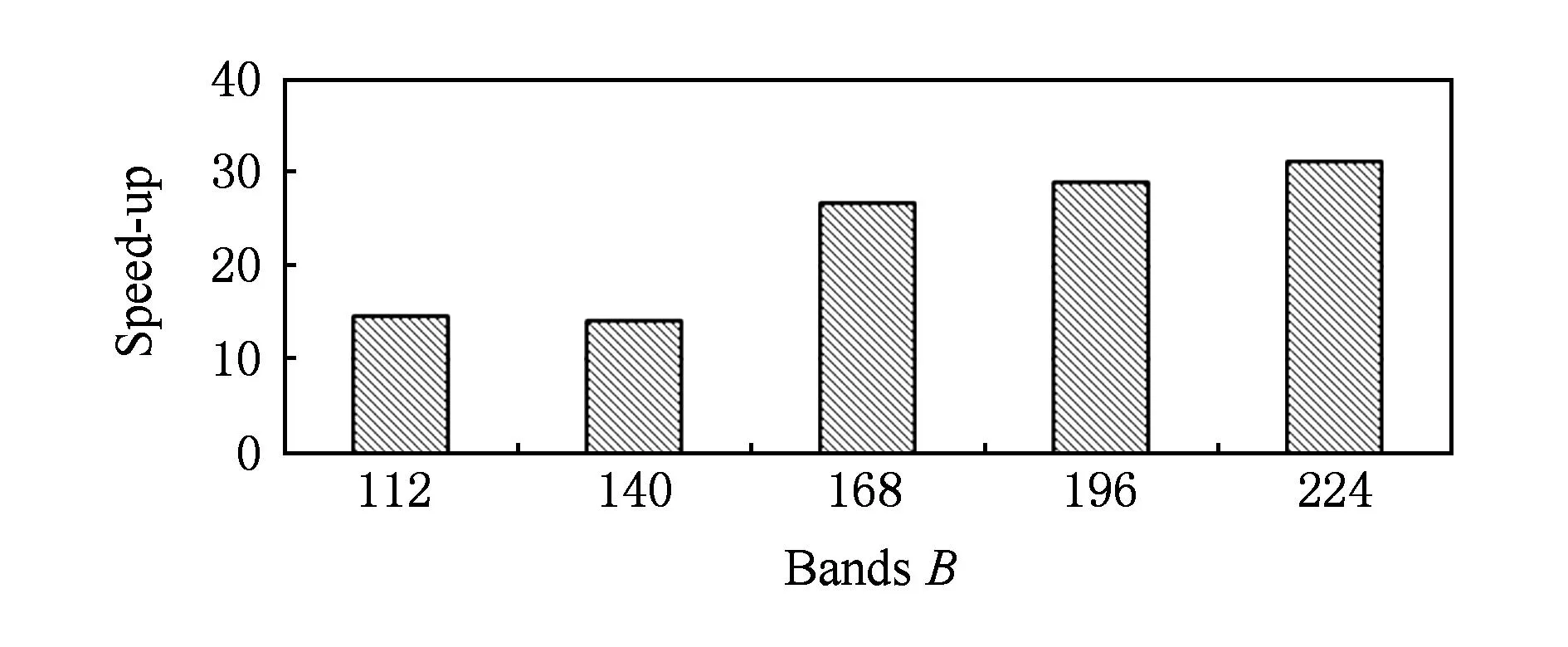
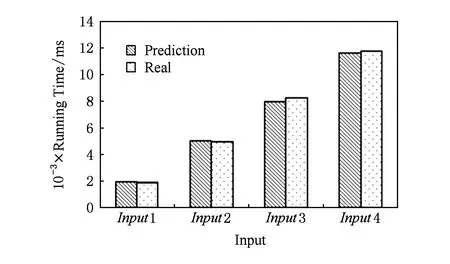
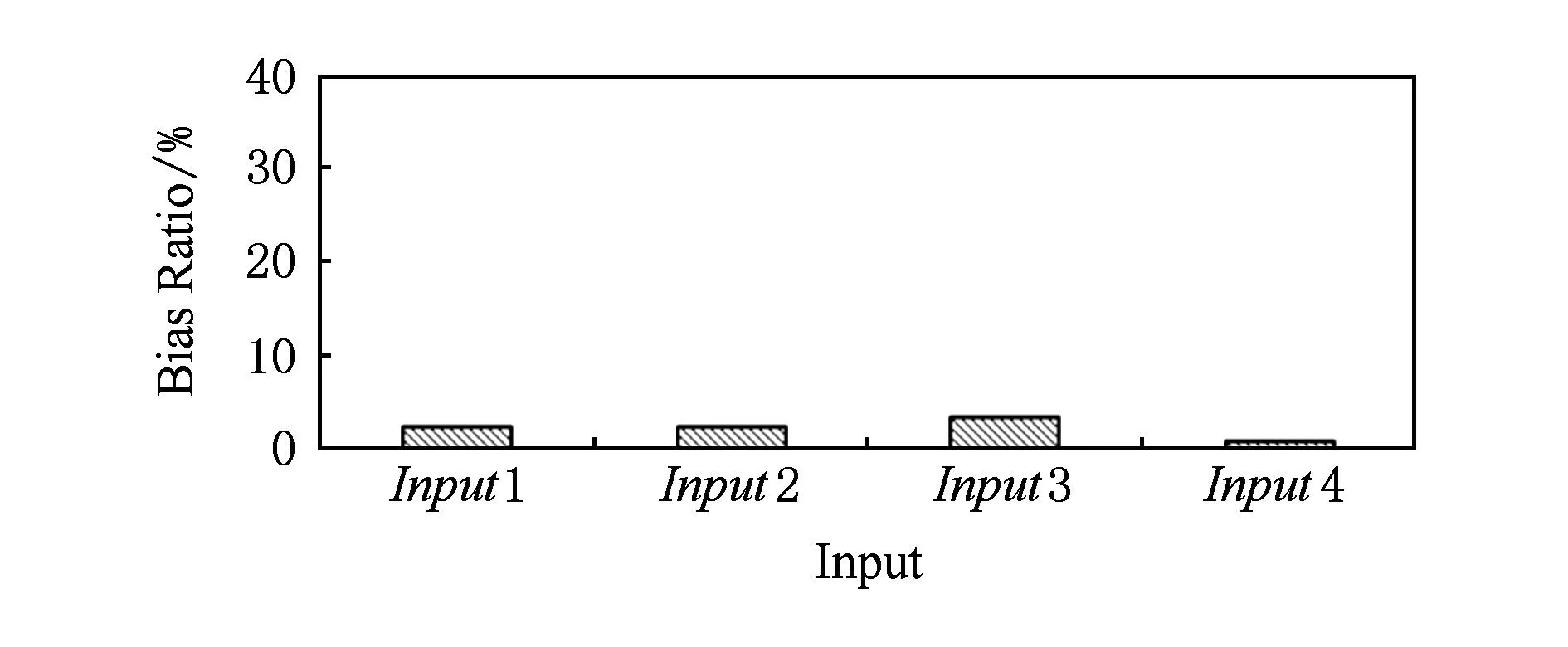
对于高光谱影像数据X(W×H×B,宽W、高H、波段(band,B)),X可看成是B行S列(S=W×H)的2维矩阵,矩阵的1行表示1个波段的高光谱影像数据.通过独立成分分析方法降维,可以获得m个IC图像,其中m 算法1. FastICA高光谱影像降维方法[17-18]. 输入:高光谱影像数据X; 输出:独立成分Y. Step1. 计算X的协方差矩阵; Step2. 计算协方差矩阵的特征值及特征向量,并根据阈值T选取最终IC图像数量m; Step3. 计算白化矩阵M=DVT,其中D为X的特征值矩阵,V为对应的特征向量矩阵; Step4. 高光谱影像数据白化处理Z=MX,这里的X为减去均值之后的X(即零均值处理); Step5. 迭代开始: Step5.1. 初始化Wi; Step5.4. 归一化Wi=Wi; Step5.5. 判断是否收敛,不收敛则转Step5.2,若收敛,如果所有的Wi已经计算结束(即i=m),则退出,否则令i=i+1,转到Step5.1计算新的Wi; Step6. 计算独立成分Y=WZ. 2.2加速热点分析 实现串行高光谱影像FastICA降维算法,对W=614,H=1087,B=224的高光谱影像降维,测试并统计计算部分(不含IO)各步骤占总计算时间的比率如表1所示.表1数据显示,Step1,Step3,Step4,Step5比重较大,共占总计算时间的99%,是本文并行研究的关键热点.分析算法过程,计算量主要集中在Step1中协方差矩阵计算、Step4中白化处理时的矩阵运算和Step5.2中Wi计算中的大量向量运算.此外Step2中特征值计算取决于B,变化不大可不考虑并行;Step3白化矩阵很小,计算量有限,不必做并行考虑;而Step6中的IC变换与W,H,m正相关,作为次要热点考虑其并行化. Table 1 Time Distribution of FastICA 3FastICA集成众核并行算法 3.1协方差矩阵任务划分 协方差矩阵是对称矩阵,仅需计算下三角阵的协方差,然后在对称的上三角阵填入对应的值.传统的并行方案是对最外层循环进行任务划分,由于是三角矩阵,将任务调度过程设定为动态调度,当线程数远小于B时,能获得较好的并行度和负载均衡;当线程数与B相当或比B大时,这种方案就会导致负载不均衡问题.本文采用的高光谱影像数据的B=224,与集成众核的硬件并发线程总数228相当,即采用传统方案并行计算协方差矩阵可能存在负载不均衡问题.为解决这一问题,本文提出一种下三角阵负载均衡方法,在本文第5节性能优化部分详细描述. 3.2白化处理与IC变换任务分配 白化处理包括白化矩阵计算和白化处理过程,其中白化矩阵维度较小、计算量也较小、无需并行,主要考虑白化处理Z=MX.针对白化处理过程,首先抽象并构建白化处理宏观模型(对算法核心计算的宏观描述),如图2所示,其中X需要进行零均值处理,构建宏观模型时暂不考虑. Fig. 2 Macroscopic model for whitening processing.图2 白化处理宏观模型 上述宏观模型可视为矩阵乘法,传统的并行矩阵乘法策略是在最外层循环做并行.但针对高光谱影像降维过程,降维后取得的波段数目m较小,而使用了硬件多线程并发技术的集成众核并行度远大于m,将导致严重的负载不均衡.因此,本文对像元素S进行任务划分,由于S=W×H足够大,可满足大量线程的并行均衡负载要求;也可采用循环合并策略进一步扩大并行度,具体优化策略参见本文第5节性能优化部分. IC变换(Y=WZ)的模型与白化处理(Z=MX)模型基本一致,因此采用与白化处理相同的并行任务划分方案和优化策略. 3.3集成众核上的ICA迭代 ICA迭代的5个步骤中,计算量主要集中在Step5.2中.该运算比较复杂,首先对其抽象,得到如图3所示的宏观模型,然后针对该模型进行并行任务分割研究. Fig. 3 Model of key step for ICA iteration.图3 ICA迭代关键步骤模型 Fig. 4 Parallel model of ICA iteration.图4 ICA迭代并行模型 3.4M-FastICA算法 基于上述热点并行任务划分策略,结合串行算法,对白化处理和ICA迭代并行宏观模型进行演绎,获得热点详细并行方案.通过第5节对比各热点并行方法在CPU与MIC上执行性能和CPU+MIC协同工作策略,提出M-FastICA并行降维算法,如图5所示,其中由于Wi正交化、归一化及判断等运算量较小,ICA迭代过程可完全Offload到MIC.算法将协方差矩阵计算、ICA迭代Offload到MIC上进行并行计算;白化处理、IC变换、转置等CPU计算占优势的步骤仍在CPU上并行处理;另外充分利用了MIC与CPU协同计算、传输计算重叠等关键异构优化策略,图5中纵向可视为时间轴,横向重叠部分可同时执行.其原理将在第5节详细讨论. Fig. 5 Flow chart of M-FastICA.图5 M-FastICA流程图 4算法性能模型 Fig. 6 Performance model of M-FastICA.图6 M-FastICA算法性能模型 本节旨在构建M-FastICA算法性能模型,通过输入高光谱影像数据参数(W,H,B,m等),经性能模型分析,预测出M-FastICA并行算法的降维时间,如图6所示: 研究M-FastICA降维算法,建立性能模型: T=TCOV+Teigen+Twhiteprocess+TICAiter+TICtrans; (1) TCOV=TCOVc+TCOVt=(BWH+ B(B+1)WH)vCOVc+(BWH+4BB)vPCI-e; (2) Twhiteprocess=(2mBWH)vwhiteprocess; (3) TICAiter=TZT×2+TeveryICA×niter≈ 2(4mWH)vPCI-e+(4mWH)vICAiter×niter; (4) TICtrans=(2mmWH)vICtrans. (5) TCOV: 协方差矩阵计算时间; TCOVc: MIC并行计算协方差矩阵时间; TCOVt: 高光谱影像数据和协方差矩阵通信时间; vCOVc: MIC计算协方差矩阵速率(图7); vPCI-e: PCI-e总线传输速率,v1版本取3 GBps; Teigen: 特征值和波段选择时间,为0.28±0.05 s; Twhiteprocess: 白化处理时间; vwhiteprocess: CPU白化处理速率,如图7所示; TICAiter: ICA迭代时间; TZT: 白化结果矩阵Z及其转置矩阵的传输时间; TeveryICA: 每次ICA迭代时间; niter: 迭代次数; vICAiter: MIC上并行ICA迭代性能,如图7所示; TICtrans: IC变换时间; vICtrans: CPU处理IC变换的速率,如图7所示: Fig. 7 Performance of different steps.图7 各步骤计算性能 MIC是高度并行计算协处理器,对并行度非常敏感,且在运算规模较大时能获得较好的吞吐率;问题规模影响并行度,对MIC性能发挥有着较大的影响.本文通过高光谱影像数据缩放,获得成比例的数据规模,测试并统计计算单元(CPU,MIC)性能.在利用该模型预测性能时,根据高光谱影像数据规模,从统计曲线中获得估计速率,再根据算法模型公式预测并行降维时间. 5面向集成众核的性能优化 本节首先对协方差矩阵计算、白化处理、ICA迭代等展开研究集成众核性能优化,然后研究了并行算法在CPU+MIC异构系统中的协同计算. 5.1协方差矩阵计算优化 针对协方差矩阵计算过程,面向集成众核架构进行优化研究,下列优化方法可加速协方差矩阵计算: 1) 数据类型选择. 高光谱影像属于图像数据,由0~255等像素信息组成,可以采用unsigned char类型(替代原始的float类型)数据存储信息,由于单位数据的存储减少,可降低协处理器访存开销和主机端设备端间通信开销. 2) 计算分解. 相对于CPU强大的事务处理能力,作为协处理器的MIC更擅长于较简单的计算.将复杂的计算任务分解为数个简单的计算,使其适用于MIC轻量级协处理器.协方差矩阵中每个元素的计算: (6) 通过式(6)的协方差计算公式变形,将协方差的计算变形为累加和点乘运算;在此基础上还能将所有协方差矩阵元素的累加提取出来单独计算,即将累加和矩阵乘运算分开进行.该计算分解过程还可减少计算量,使计算量从2B(B+1)WH降为BWH+B(B+1)WH,减少了近半.算法2和算法3分别描述了计算分解前后协方差矩阵计算的详细过程. 算法2. 计算分解前的协方差矩阵计算. 输入:高光谱影像数据X; 输出:协方差矩阵cov. parallel fori=0 to (B-1)*B为波段数* forj=0 toi*下三角* fork=0 toS*S=W×H像元数* x=X[i][k]; y=X[j][k]; m+=x;n+=y; r+=x×y; end for cov[i][j]=(r-m×nS)(S-1);*计算协方差* cov[j][i]=cov[i][j];*上三角阵赋值* end for end parallel for 算法3. 计算分解后的协方差矩阵计算. 输入:高光谱影像数据X; 输出:协方差矩阵cov. parallel fori=0 to (B-1) fork=0 toS m[i]+=X[i][k];*计算累加* end for end parallel for parallel fori=0 to (B-1) forj=0 toi fork=0 toS r+=X[i][k]×X[j][k];*计算矩阵乘* end for cov[i][j]=(r-m[i]×m[j]S)(S-1);*计算协方差* cov[j][i]=cov[i][j];*上三角阵赋值* end for end parallel for Fig. 8 Load balancing for lower triangular matrix.图8 下三角阵负载均衡 3) 下三角阵负载均衡. 协方差矩阵是对称阵,仅需计算下三角阵,由于MIC核心较多,2.2节的并行方案无法合理地做到下三角阵的负载均衡,如线程0执行1个协方差计算,而线程223需要执行224个协方差计算.为实现下三角阵的负载均衡,本文设计了一种新的负载均衡方法,如图8所示.其基本思想是将三角形状的2维计算任务映射为1维计算任务,然后对得到的1维计算任务进行并行划分,最终实现均衡负载的目的.本文通过图8中行③和行④的公式,将1维索引映射到1维数组中,把2层循环合并为1层循环,不仅可以实现负载均衡,还可增大并行度.算法4采用了下三角阵负载均衡策略. 算法4. 下三角负载均衡后的协方差矩阵计算. 输入:高光谱影像数据X; 输出:协方差矩阵cov. parallel fori=0 to (B-1) fork=0 toS m[i]+=X[i][k];*计算累加* end for end parallel for parallel forii=0 to (n-1) i=ceil((sqrt(9.0+8×ii)-3)2); j=ii-(1+i)×i2; fork=0 toS r+=X[i][k]×X[j][k];*计算矩阵乘* end for cov[i][j]=(r-m[i]×m[j]S)(S-1);*计算协方差* cov[j][i]=cov[i][j];*上三角阵赋值* end parallel for 程序经上述优化方法优化后进行实验测试,其效果如图9所示,图9中0表示未采取优化手段,1~3分别表示相继采用优化手段1~3后的时间消耗. Fig. 9 Optimization effect of COV calculation.图9 COV计算优化效果 5.2白化处理集成众核优化 针对白化处理过程,本文采取的优化方法包括: 1) 并行循环选择.高光谱影像白化处理过程有其独特的特点,最外层循环量是根据贡献率所取得的波段数目m,该值往往为十几到几十不等,该层循环并行度较小,不适合在众核处理器(MIC上有50多个核,每个核可并发4个线程)上并行.选择适合众核架构核数的并行度的循环开发并行至关重要.本文选择第2层循环开发并行,其并行度(S=W×H)巨大. 2) 数据类型选择.同协方差矩阵计算过程. 3) 循环交换.当存储访问不连续时,cache命中率低,将导致大量的内存访问开销;最内层循环无法向量化时,MIC的重要部件向量处理单元(vector process unit, VPU)得不到有效利用,将大大影响性能.若程序存在上述2方面情况,需要循环交换.白化处理由于存储访问不连续而采取循环交换措施,通过交换内2层循环使数据连续访问. 4) 除最内层的嵌套循环展开.白化处理共3层循环,最外层取值m(降维后取得的波段数)较小而不适合MIC并行,通过将外2层嵌套循环展开,增加最外层循环次数,使其适用于MIC等众核架构,还能减少并行区域fork-join开销.在嵌套循环展开的同时保持最内层循环不变,以此来保证向量化和连续存储访问. 5) 高光谱影像矩阵转置.白化处理对高光谱影像矩阵的访问是按列的,为了使访问存储连续,可以采用矩阵转置的策略.通过转置,原始矩阵行列交换,实现存储连续访问.该方案将引入转置开销,若转置开销大于性能收益,则不可取(效果统计时已包含转置开销). 优化方法3和优化方法5无法重复使用,因其目的是一致的,即连续访存.图10所示6种不同优化方法组合效果,其中组0没有优化,组1用了方法1,组2用了方法1和方法2,组3采取方法1至方法3,方法1~4组成组4,组5用了方法1、方法2、方法5优化方法,组6采用方法1、方法2、方法4、方法5.通过一系列的优化,组6获得最佳性能. Fig. 10 Optimization effect of whitening process.图10 白化处理优化效果 5.3ICA迭代优化 ICA迭代部分包含大量的小规模迭代计算,本文对单次迭代展开优化研究,主要采取3种优化策略: 2) ICA迭代过程中,参与计算的Wi是W矩阵的1列,迭代过程中Wi参与大量计算,因此本文采用中间数组存储Wi中元素参与计算.C语言中矩阵是按行存储的,列访问导致Cache命中率下降.利用中间数组tmp[]存储Wi的元素,那么运算时访存是顺序的,Cache命中率高,从而提升程序性能. 3) 使用较底层的intrinsics函数,显式地指定数据向量化处理过程,以充分发挥MIC中向量处理单元的性能.intrinsics函数是类汇编函数,指定程序中的向量运算,比如向量内积(c=A·B)运算时,普通C程序代码和intrinsics代码如下所示: C版向量内积: for(i=0;i c+=a[i]+b[i]; endfor intrinsics版向量内积: _m512_a,_b,_c; for(i=0;i _a=_mm512_load_ps(&a[i]); _b=_mm512_load_ps(&b[i]); _c=_mm512_add_ps(_c,_mm512_mul_ps(_a,_b)); endfor c=_mm512_reduce_add_ps(_c); 其中intrinsics代码中,1条指令完成16个浮点数的运算. 在程序中分别实现上述优化方法,测试出各优化方法使用前后ICA迭代步骤的时间消耗,获得图11所示的优化效果,其中横坐标0表示未采取优化措施,1~3分别表示相继采用优化方法1~3后的时间. Fig. 11 Optimization effect of ICA iteration.图11 ICA迭代优化效果 1) 异构协同计算优化.CPU+MIC架构是典型的异构系统,CPU和MIC可同时进行计算或通信,通过协同计算可掩盖部分步骤处理时间.本文算法中,协方差矩阵计算(COV)和高光谱影像数据X转置的过程可同时执行,如图12所示;白化结果矩阵Z的传输可与矩阵Z转置同时执行,如图13所示.通过上述CPU与MIC协同工作,可以掩盖X和Z的转置开销. Fig. 12 Cooperative computing between COV and X transposition.图12 COV与X转置协同计算 Fig. 13 Transpose Z and transfer Z at the same time.图13 Z转置与通信重叠 Fig. 14 Performance ratios of MICCPU for different steps.图14 各步骤MICCPU性能对比 2) CPU与MIC计算的权衡.CPU和MIC都是异构系统中重要的计算资源,由于体系结构的不同,其擅长领域也不同.本文通过实验统计,获得各步骤MIC与CPU上执行时间比值(图14中横轴1~6分别表示COV、X转置、白化处理、Z转置、ICA迭代和IC变换).比值大于1时CPU计算有优势,小于1则Offload到MIC能获得更好的性能.观察图14,当数据较大时,COV过程Offload到MIC合适,ICA迭代过程Offload到MIC可获得更好的性能,其他过程在CPU端处理更划算. 6实验结果与分析 6.1实验准备 本文测试平台是天河2号超级计算机.天河2号单个节点搭载2个12核Xeon E5-2692v2 CPU和57核Intel Phi 31S1P协处理器.根据热点并行方案和优化策略,采用OpenMP和LEO(language extensions for offload)的C语言扩展来实现M-FastICA并行算法,采用Intel C Compiler 2013 sp1.1.106编译器、O3编译选项,最后在天河2号单节点上测试性能. 表2罗列了本文采用的AVIRIS高光谱影像数据的详细信息,共4组. Table 2 Information of Hyperspectral Image Data 由于高光谱影像数据和ICA迭代过程中取得的随机数不同,导致ICA迭代次数不同,不同的迭代次数将导致消耗的时间也不同.为了获得准确的性能对比数据,本文约定:同一数据取固定的迭代次数.通过多次实验求平均值的方法,确定各组数据的迭代次数,如表3所示: Table 3 Iteration Number of Hyperspectral Image Data 6.2并行算法加速比 本实验分别在MIC和CPU上测试并行程序计算时间,与打开最佳优化开关(O3)的串行程序对比,获得加速比绘制成图15.其中MIC启动时间和MIC上存储分配时间是一次性开销,不计入本文时间统计范畴.图15中处理高光谱影像数据1时,CPU上的加速比高于MIC,可知CPU比MIC更擅长于处理小规模运算;高光谱影像数据2~4中,MIC获得了比CPU并行更高的性能,说明MIC适合规模较大的计算;在处理高光谱影像数据4时,M-FastICA算法可获得42倍加速比,比24核CPU并行快2.2倍. Fig. 15 Speed-up of MIC and CPU.图15 MIC与CPU加速比 6.3波段数与性能的探讨 本文选用的AVIRIS高光谱影像数据中B=224,刚好与Intel Phi 31S1P协处理器的硬件线程数量228接近,因此会提出疑问,如果B变化时是否会影响并行程序性能? 当B发生变化时,各热点的计算量也会产生变化,因此并行程序性能会有所变化,但总体稳定.究其原因,本文对各热点的并行程序进行了大量深入优化,比如下三角矩阵均衡负载、循环合并等,已经将受B限制的并行度进行了扩展,并行粒度不会受B变化而发生较大变化. Fig. 16 Speed-ups with different bands.图16 波段数与加速比的关系 本文通过控制变量法验证B与性能的关系.选取输入高光谱影像数据3,取其中前112,140,168,196,224波段的影像数据作为输入数据,通过实验统计并行算法对最优串行的加速比,如图16所示.图16中B=112和B=140时,其加速比较小,原因是这2组输入降维时最终IC图像数量为5,6,而其他几组输入降维时最终IC图像数量为13,14,这会影响白化处理、ICA迭代和IC变化等过程的计算量及性能.而当IC图像数量不变时,程序性能基本稳定,不会因B的变化而影像程序性能. 6.4算法性能模型验证 将高光谱影像数据的参数(B,W,H,m)输入M-FastICA算法性能模型,通过式(1)~(5)计算可得到预测时间;执行优化后的并行程序,获得实际运行时间,如图17所示.对比预测时间和执行时间的误差,图18所示为误差百分比.图17显示预测时间与真实运行时间基本一致,图18显示预测性能和实测性能最大误差小于5%,说明本文提出的M-FastICA算法性能模型能较准确地预测算法性能. Fig. 17 Time of real and perdiction for M-FastICA model.图17 M-FastICA模型预测与实测时间 Fig. 18 Bias ratio of the M-FastICA model.图18 M-FastICA性能模型预测误差 6.5并行算法瓶颈分析 Fig. 19 Time distribution of M-FastICA.图19 M-FastICA时间分布 统计独立成分分析降维算法各个步骤消耗时间占总时间的百分比,绘制成图19(横轴1~5分别表示独立成分分析的5个关键步骤:协方差矩阵计算、特征值特征向量计算、白化处理、ICA迭代、IC变换).对比图19和表1,我们发现并行后各步骤耗时比重有所改变,但协方差矩阵计算和ICA变换依旧是算法性能瓶颈.要解决这一瓶颈,可以通过扩展计算资源来解决,比如使用MIC集群,这也是下一步工作的重点. 7结论 本文基于集成众核MIC研究高光谱影像FastICA降维方法,设计了协方差矩阵计算、白化处理、ICA迭代、IC变换等热点并行方案和优化策略;提出和实现了基于MIC的M-FastICA算法,给出算法性能模型并验证其准确性.实验结果显示M-FastICA算法获得了良好的性能提升,对比最优串行程序最高可加速42倍,比24核CPU多线程快2.2倍. 本文研究显示,高光谱影像FastICA降维算法可在集成众核架构上获得良好的性能,但仍存在性能瓶颈,可考虑进一步将算法扩展到MIC集群以突破性能瓶颈. 参考文献 [1]Green R O, Eastwood M L, Sarture C M, et al. Imaging spectroscopy and the airborne visibleinfrared imaging spectrometer(AVIRIS)[J]. Remote Sensing of Environment, 1998, 65(3): 227-248 [2]Green A A, Berman M, Switzer P, et al. A transformation for ordering multispectral data in terms of image quality with implications for noise removal[J]. IEEE Trans on Geoscience and Remote Sensing, 2000, 26(1): 65-74 [3]Kaarna A, Zemcik P, Kalviainen H, et al. Compression of multispectral remote sensing images using clustering and spectral reduction[J]. IEEE Trans on Geoscience and Remote Sensing, 2000, 38(2): 1073-1082 [4]Scott D W, Thompson J R. Probability density estimation in higher dimensions[C]Proc of the 15th Symp on the Interface of Computer Science and Statistics. Amsterdam: North-Holland, 1983: 173-179 [5]Jolliffe I T. Principal Component Analysis[M]. Berlin: Springer, 2002 [6]Hyvärinen A, Oja E. Independent component analysis: Algorithm and applications[J]. Neural Networks, 2000, 13(45): 411-430 [7]Tenenbaum J, De Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323 [8]Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500): 2323-2326 [9]Wang Heyong, Zheng Jie, Yao Zheng’an, et al. Application of dimension reduction on using improved LLE based on clustering[J]. Journal of Computer Research and Development, 2006, 43(8): 1485-1490 (in Chinese)(王和勇, 郑杰, 姚正安, 等. 基于聚类和改进距离的LLE方法在数据降维中的应用[J]. 计算机研究与发展, 2006, 43(8): 1485-1490) [10]Jeffers J, Reinders J. Intel Xeon Phi Coprocessor High Performance Programming[M]. Amsterdam: Elsevier, 2013(in Chinese)(James J, James R. Intel Xeon Phi协处理器高性能编程指南[M]. 陈健, 等译. 北京: 人民邮电出版社, 2013) [11]Meuer H, Strohmaier E, Dongarra J, et al. TOP500 supercomputer sites[EBOL]. 2014 [2014-09-26]. http:www.top500.orglists201406 [12]Valencia D, Lastovetsky A, O’Flynn M, et al. Parallel processing of remotely sensed hyperspectral images on heterogeneous networks of workstations using HeteroMPI[J]. International Journal of High Performance Computing Applications, 2008, 22(4): 386-407 [13]Plaza J, Plaza A, Pérez R, et al. Parallel classification of hyperspectral images using neural networks[J]. Computational Intelligence for Remote Sensing Studies in Computational Intelligence, 2008, 133: 193-216 [14]Sánchez S, Ramalho R, Sousa L, et al. Real-time implementation of remotely sensed hyperspectral image unmixing on GPUs[JOL]. Journal of Real-Time Image Processing, 2012 [2014-09-26]. http:link.springer.comarticle10.1007s11554-012-0269-2 [15]Platoš J, Gajdoš P, Krömer P, et al. Non-negative matrix factorization on GPU[C]Proc of the 2nd Int Conf on Networked Digital Technologies. Berlin: Springer, 2010: 21-30 [16]Ramalho R, Tomas P, Sousa L. Efficient independent component analysis on a GPU[C]Proc of the 10th IEEE Int Conf on Computer and Information Technology. Piscataway, NJ: IEEE, 2010: 1128-1133 [17]Hyvrinen A. Fast and robust fixed-point algorithms for independent component analysis[J]. IEEE Trans on Neural Networks, 1999, 10(3): 626-634 [18]Hyvrinen A. The fixed-point algorithm and maximum likelihood estimation for independent component analysis[J]. Neural Processing Letters, 1999, 10(1): 1-5 Fang Minquan, born in 1989. PhD candidate. Student member of China Computer Federation. His main research interests include parallel computing and data assimilation. Zhang Weimin, born in 1966. Professor and PhD supervisor. His main research interests include parallel computing and data assimilation. Zhou Haifang, born in 1975. Professor. Member of China Computer Federation. Her main research interests include parallel computing and image processing. Parallel Algorithm of Fast Independent Component Analysis for Dimensionality Reduction on Many Integrated Core Fang Minquan, Zhang Weimin, and Zhou Haifang (CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073) AbstractThere are massive matrix and iterative calculations in fast independent component analysis (FastICA) for hyperspectral image dimensionality reduction. By analyzing hotspots of FastICA algorithm, we design the parallel schemes of covariance matrix calculating, whitening processing and ICA iteration on many integrated core (MIC), implement and validate an M-FastICA algorithm. Further, we present a performance model for M-FastICA. We present a series of optimization methods for the parallel schemes of different hotspots: reforming the arithmetic operations, interchanging and unrolling loops, transposing matrix, using intrinsics and so on. In particular, we propose a novel method to balance the loads when dealing with the lower triangular matrix. Then we measure the performance effects of such optimization methods. Our experiments show that the M-FastICA algorithm can reach a maximum speed-up of 42X times in our test, and it runs 2.2X times faster than the CPU parallel version on 24 cores. We also investigate how the speed-ups change with the bands. The experiment results validate our performance model with an acceptable accuracy and thus can provide a roofline for our optimization effort. Key wordsmany integrated core (MIC); independent component analysis (ICA); dimensionality reduction of hyperspectral image; performance model; load balancing of lower triangular matrix 收稿日期:2014-09-29;修回日期:2015-04-16 基金项目:国家自然科学基金项目(61272146,41375113); 湖南省研究生创新资助项目(CX2015B030) 中图法分类号TP391.4 This work was supported by the National Natural Science Foundation of China (61272146,41375113) and the Graduate Innovative Foundation of Hunan Province of China (CX2015B030).