基于分支相关性分析的不可达路径检测方法
2016-06-16姜淑娟史娇娇张艳梅鞠小林钱俊彦
姜淑娟 韩 寒 史娇娇 张艳梅,2 鞠小林,3 钱俊彦
1(中国矿业大学计算机科学与技术学院 江苏徐州 221116)2(计算机软件新技术国家重点实验室(南京大学) 南京 210023)3(南通大学计算机科学与技术学院 江苏南通 226019)4(广西可信软件重点实验室(桂林电子科技大学) 广西桂林 541004)(shjjiang@cumt.edu.cn)
基于分支相关性分析的不可达路径检测方法
姜淑娟1,4韩寒1史娇娇1张艳梅1,2鞠小林1,3钱俊彦4
1(中国矿业大学计算机科学与技术学院江苏徐州221116)2(计算机软件新技术国家重点实验室(南京大学)南京210023)3(南通大学计算机科学与技术学院江苏南通226019)4(广西可信软件重点实验室(桂林电子科技大学)广西桂林541004)(shjjiang@cumt.edu.cn)
摘要软件测试中,不可达路径的存在会导致测试资源浪费,有效地检测程序中的不可达路径有助于节约测试资源、提高测试效率.分支相关性的存在是不可达路径产生的主要起因.因此,确定分支的相关性在不可达路径的检测中占据十分重要的地位.提出了一种利用关联分析和数据流分析确定分支相关性的方法,进而实现不可达路径的自动检测.首先,结合静态分析和动态分析,构建反映程序中各分支判断语句静态依赖关系和动态执行信息的数据集;然后,利用关联分析和数据流分析技术确定分支的相关性;最后,根据分支相关性信息检测不可达路径.基于一组基准程序和开源程序,开展不可达路径检测实验.实验结果表明,该方法能够准确地检测出程序中的不可达路径,可以有效地提高软件测试的效率.
关键词软件测试;不可达路径;分支相关性;关联分析;数据流分析
许多软件测试问题都可以归结为面向路径的测试数据生成问题[1],而不可达路径的存在是路径测试中的一个难题,因为没有输入数据能经过这些不可达路径,从而导致测试数据生成阶段大量人力和资源的浪费.因此,路径的可达性直接影响着路径测试的效率和充分性,有效地检测出这些不可达路径不仅能够降低测试成本,而且能提高测试效率.然而,不可达路径的检测是一个不可判定的问题[2].目前,不可达路径检测方法主要分为静态检测方法[3-14]和动态检测方法[15-17]2类.其中静态检测方法可划分为基于路径条件可满足性的检测方法[3-9]和基于分支相关性分析的检测方法[10-14],前者针对每条路径,通过对满足路径条件的谓词组合进行求解来判定路径的可达性,复杂度较高;后者通过分析分支语句间是否存在相关性来检测不可达路径.Bodik等人[10]指出分支相关性的存在是不可达路径产生的主要起因.在一段复杂程序中,有9%~40%的分支语句具有相关性,但是该类方法无法分析具有复杂结构的条件谓词,因此其分支节点覆盖率较低[18].而动态检测方法通常在面向目标路径生成测试数据阶段完成对路径可达性的判断,其计算代价较大,并且检测结果具有较强的不确定性.
关联分析是一项较为成熟的技术,其目的是在海量数据集中发现数据间的关联信息.在程序分析时采用关联分析技术,有助于以较低的时间和空间代价更快、更准确地从大量的分支判断语句执行信息中获取程序分支的相关信息.在关联分析的基础上对程序进行数据流分析,并开展不可达路径的检测,可以有效提高检测精度.因此本文提出一种结合关联分析和数据流分析2种技术确定分支相关性的策略,进而自动检测程序中的不可达路径.本文的方法结合了静态分析方法和动态分析方法的优势,既可以避免单纯使用静态分析方法带来的分支节点覆盖率较低的缺陷,又可以降低动态分析方法导致的高昂代价.实验表明:本文的方法能够准确地检测出程序中的不可达路径,可以有效地提高软件测试的效率.
本文的主要贡献如下:
1) 提出了一种动静态结合的不可达路径检测方法,有效结合了静态分析和动态分析的优势;
2) 提出了一种分支相关性确定方法,将分支相关性分为B-B相关性和A-B相关性,首先利用关联分析的方法获取B-B相关性信息,并在此基础上利用静态数据流分析技术获取纯A-B相关性信息,提高了不可达路径的检测精度;
3) 实验验证了本文方法的有效性.
1预备知识
在介绍不可达路径的检测方法之前,本节首先给出不可达路径及关联分析相关的一些基本概念.
定义1.控制流图.控制流图(control flow graph, CFG)是程序中语句逻辑执行的一种图形化表示,可由四元组(N,E,s,f)表示.其中,N为节点的集合,表示程序中的语句;E⊆N×N为边的集合,表示程序中语句间的控制关系;s为程序的入口节点;f为程序的出口节点.
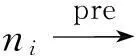
定义3.控制树[19](predominator tree,PRT).在CFG中,除s外,其他任何节点都有一个直接控制.根据该控制关系,可构成一棵以s为根节点的控制树.控制树可由三元组(N,E,s)表示,其中E={(idom(ni),ni)|ni∈N-{s}}.
定义4.控制树主干(main trunk of predominator tree,MTPRT).在控制树中,由出口节点及其在控制树中的所有祖先节点构成的节点序列为控制树主干.
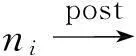
定义6. 蕴含树[19](postdominator tree, POT).在CFG中,除f外,其他任何节点都有一个直接蕴含.根据该蕴含关系,可构成一棵以f为根节点的蕴含树.蕴含树可由三元组(N,E,f)表示,其中,E={(iimp(ni),ni)|ni∈N-{f}}.
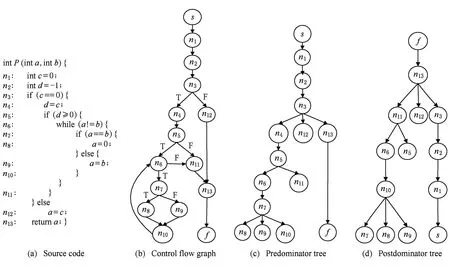
Fig. 1 An example P.图1 函数P的示例
定义7. 循环节点.对于控制流图CFG中的节点ni,若存在节点nj(i≠j),使得nj在CFG对应的蕴含树和控制树中皆是ni的子节点,则节点ni为循环节点.
定义8. 路径.路径为CFG中的一个执行序列path=(n1,n2,…,nm),其中m为路径的长度,(ni,ni+1)∈E(i=1,2,…,m-1),若n1=s,nm=f,则path为一条完整路径,本文中所指的路径均为完整路径.若存在一组输入数据,使得程序能沿路径path执行,则path为可达路径,否则path为不可达路径.
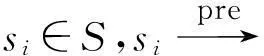
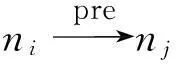
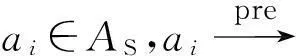
定义10. 冲突子路径.由程序中存在冲突的语句构成的语句序列称为冲突子路径.根据产生冲突的语句类型,可分为B-B冲突子路径和A-B冲突子路径.
1) B-B冲突子路径.设ni和nj是2个分支判断语句,如果(ni,nj)有T→T(或T→F)的B-B相关性,则ni(T)→nj(F)(或ni(T)→nj(T))构成B-B冲突子路径;同样,如果(ni,nj)有F→T(或F→F)的B-B相关性,则ni(F)→nj(F)(或ni(F)→nj(T))构成B-B冲突子路径.
2) A-B冲突子路径.设n为分支判断语句,AS为赋值语句集,如果(AS,n)具有&→T(或&→F)的A-B相关性,则AS→n(F)(或AS→n(T))构成A-B冲突子路径.
为了更加清晰地理解上述概念,下面通过图1所示的例子进行具体的说明.
例1. 图1(a)为一段由Java语言编写的程序P,图1(b)为其相应的控制流图,s,f分别为其入口节点和出口节点.
根据控制流图中的控制关系和蕴含关系,可以分别得到图1(c)所示的控制树和图1(d)所示的蕴含树,其中,控制树主干MTPRT={s,n1,n2,n3,n13,f}.对于节点n6,由于节点n7,n8,n9,n10在控制树和蕴含树中皆是节点n6的子节点,因此节点n6为循环节点.对于节点n6和n7,因为当节点n6的取值为真时,节点n7的取值必为假,因此(n6,n7)有T→F的B-B相关性.对于路径path=(s,n1,n2,n3,n4,n5,n6,n7,n8,n10,n6,n11,n13,f),由于path经过n6(T)和n7(T),不会有任何一组输入数据能使得程序沿该路径执行,因此路径path为1条不可达路径,而n6(T)→n7(T)则构成1条B-B冲突子路径.对于语句n5,由于赋值语句n1,n2,n4使得语句n5中d≥0取固定值T,因此,({n1,n2,n4},n5)具有&→T的A-B相关性,然而由于n4∉MTPRT,因此({n1,n2,n4},n5)之间&→T的A-B相关性可转化为(n3,n5)之间T→T的伪B-B相关性.对于语句n3,由于赋值语句n1使得语句n3中谓词c==0取固定值T,因此,(n1,n3)具有&→T的A-B相关性,该A-B相关性不能转化为B-B相关性,因此(n1,n3)具有&→T的纯A-B相关性,而n1→n3(F)则构成1条A-B冲突子路径.
定义11. 关联规则[21].给定:
① 项的集合(itemset):I={i1,i2,…,in};
② 任务相关的事务数据集D,其中,每个事务TS是I的非空子集,即满足TS⊆I;
③ 每个事务对应唯一的事务标识符TID;
④X,Y为2个项集,若X⊂I,Y⊂I,并且X∩Y=∅,则关联规则的蕴涵式为
X⟹Y[support,confidence],
其中,规则X⟹Y在事务数据集D中成立,X为规则的前项集,Y为规则的后项集,support和confidence分别表示X⟹Y的支持度和置信度.其中,支持度为D中事务包含X∪Y的概率;置信度为D中包含X的事务中同时又包含Y的概率,即条件概率.
满足最小支持度(min_support)和最小置信度(min_confidence)的关联规则称为强关联规则.最小支持度和最小置信度按需设定.此外,支持度不小于最小支持度的项集称为频繁项集.
2不可达路径检测方法
本节提出了一种不可达路径的自动检测方法.1)结合静态分析和动态分析,构建反映各分支判断语句静态依赖关系和动态执行信息的数据集;2)通过关联分析方法确定B-B相关性信息,在此基础上利用数据流分析技术确定纯A-B相关性信息;3)根据分支相关性检测不可达路径.
2.1系统模型
不可达路径检测方法分为3个阶段:①构建数据集;②确定分支相关性;③检测不可达路径.系统模型如图2所示:
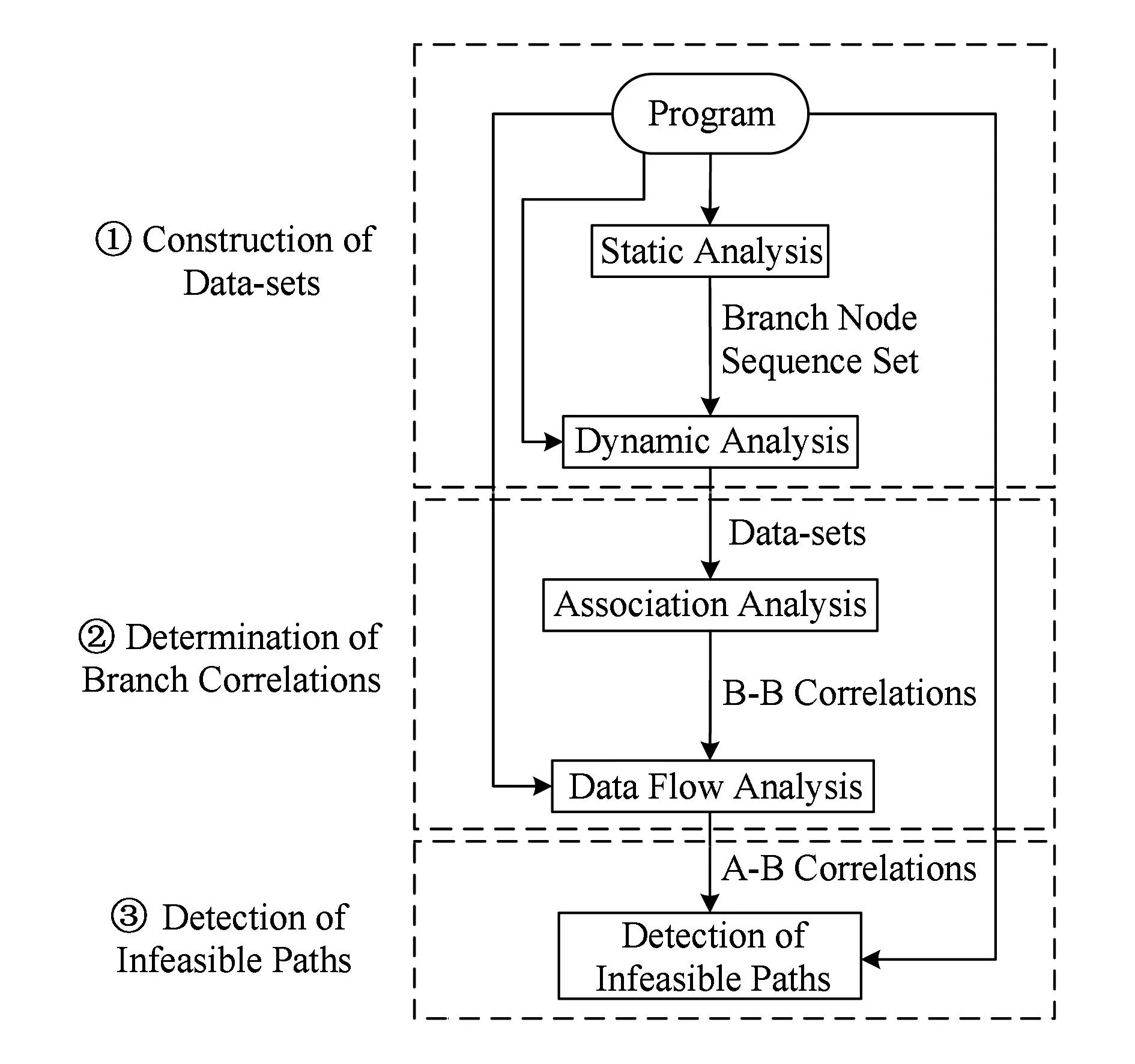
Fig. 2 Framework of our method.图2 系统模型
阶段1. 构建数据集.采用静动态结合的方法,构建反映各分支判断语句静态依赖关系和动态执行信息的数据集.首先对程序进行静态分析,获取分支节点序列集;然后采用动态分析方法,收集程序执行时分支判断语句的动态信息,以得到关联分析所需的数据集.
阶段2. 确定分支相关性.首先利用关联分析技术对数据集进行分析,确定包含伪B-B相关性在内的B-B相关性;然后利用数据流分析方法,并结合B-B相关性信息,确定纯A-B相关性信息.
阶段3. 检测不可达路径.根据分支相关性信息确定冲突子路径,进而检测程序中的不可达路径.将不可达路径的检测运用到软件测试中,从而节约测试资源、提高测试效率.
2.2数据集的构建
在本节中,我们利用动静态相结合的方法对源程序进行分析,构建反映各分支判断语句静态依赖关系和动态执行信息的数据集.
首先,利用Soot①对程序进行静态分析,构建程序的控制流图、控制树及蕴含树,然后通过搜索控制树获取具有控制关系的分支节点序列集U,U满足4个条件:
1)U覆盖控制流图中的全部分支节点;
2) ∀ui∈U,ui包含了控制树主干中的每一个分支节点;
3) ∀ui∈U,存在一条路径pathi,使得pathi包含了ui中的每一个节点;
4) ∀ui∈U,∀uj∈U,ui≠uj,其中i≠j.
∀ui∈U,采用动态分析技术,通过JDI(Java debug interface)②监听序列ui中各个分支节点ni 1,ni 2,…,ni k的执行情况,在输入域内随机获取M个抽样输入数据,要求当程序输入每个抽样数据时ni 1,ni 2,…,ni k全部执行,若存在某节点nix不执行,则换取其他抽样值,直到所有的分支节点都执行.在随机抽样时,我们会使各抽样值均匀分布在输入域内.如果∃ui∈U,利用随机抽样不能使ui中的所有分支节点都执行,本文将不会对ui构建相应数据集.因为经过前期的多次实验,对于不同的ui,随机抽样并执行程序,如果出现不能使得ui中的所有分支节点都执行的情况,则会改进抽样方法,适时调整抽样的子区域,若仍有上述情况发生,则对ui进行手动分析.
M值的设定对于实验结果存在着一定的影响,该值增大时可能但不一定会提高不可达路径的检测精度,但会增加检测的复杂度,值太小时则会降低检测精度,增加漏报和误报情况的发生,本文中M值主要根据分支节点序列中节点的个数和输入参数的个数进行设定,设序列中分支节点的个数为n,输入参数的个数为k,则统计数据量设为k×2n+1.
为了提高算法的效率,我们仅记录并分析各分支节点的信息.∀ui∈U,分析当程序输入抽样值Ii j时ui中各分支节点的取向(TF),从而得到抽样值Ii j对应的分支节点取值序列pi j,依此类推,获取M个抽样值的分支节点取值序列集vi.为了避免路径数目过于庞大,对于循环次数较多的循环语句,我们限制其执行次数不超过3,并记录其每次执行时的取值情况.最终分支节点序列集U将得到一个分支节点取值序列集的集合V,即
V={v1,v2,…,vi}={{p11,p12,…,p1 M},
{p21,p22,…,p2 M},…,{pi 1,pi 2,…,pi M}},
其中,pi j是当程序输入抽样值Ii j时ui中各分支节点的取值序列,pi j中的每个元素取值为TF.

算法1.分支节点取值序列集的获取算法.
Function:GetCSValue(TP,PRT)
输入:待测程序TP、待测程序的控制树PRT;
输出:分支节点取值序列V.
①V=∅;
②U=∅;
③c=f;
④ do
⑤l=c;
⑥c=c.PRTParentNode;
⑦Analyze(c,l);
⑧ while (c.PRTParentNode!=NULL);
⑨ for (eachui∈U) do
⑩ for (intj=1;j≤M;j++) do




procedureAnalyze(PRTNodec,PRTNodel)

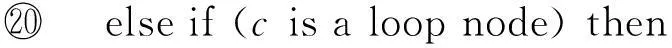




获取分支节点取值序列集的集合V之后,对其进行关联分析之前,∀vi∈V,需要将vi转换为关联分析所需的数据集.∀vi∈V,按如下方式将vi转化为数据集Di,即:

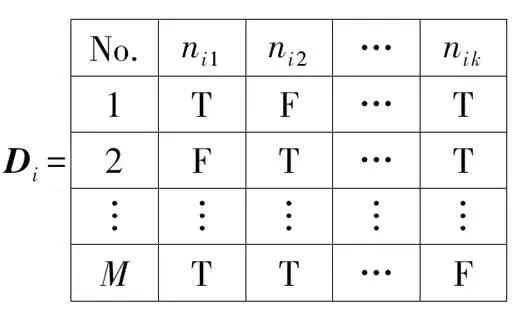
No.ni1ni2…nik1TF…T2FT…T︙︙︙︙︙MTT…F
其中:
2.3分支相关性的确定
本节首先利用关联分析技术对数据集进行分析,确定包含伪B-B相关性在内的B-B相关性,然后利用数据流分析方法,并结合B-B相关性信息,确定纯A-B相关性信息.
2.3.1基于关联分析的B-B相关性的确定
本节对数据集进行关联分析,从而确定包含伪B-B相关性在内的B-B相关性信息.∀Di∈D,首先从数据集Di中找出所有的频繁项集,然后再由频繁项集产生强关联规则.我们对传统的强关联规则生成算法[21]进行了改进,避免生成无用的强关联规则,使其更适用于B-B相关性的确定,从而提高算法的效率和精度.
对Di进行关联分析之前,需要设定min_support和min_confidence,2值的设定直接影响得到B-B相关性信息的可靠性和正确率,结合B-B相关性的定义和特点,令:
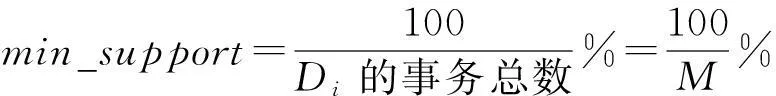
min_confidence=100%.
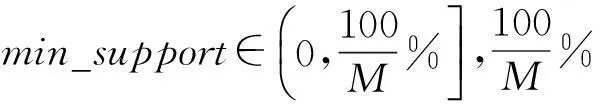
1) 从Di中找出所有的频繁项集
从数据集Di中,找出所有满足支持度大于等于min_support的频繁项集.以2-项集{ni=T,nj=F}为例,其支持度为
support({ni=T,nj=F})=

(1)
我们采用FP-Growth[22]算法对数据集进行分析.FP-Growth算法采用分治的方法,首先读取数据集Di,构造频繁1-项集及FP-Tree;然后将FP-Tree分解成一些条件模式基(conditional pattern base, CPB)(频繁项在FP-Tree中的所有节点祖先路径的集合),每个CPB和1个频繁1-项集相关联,根据CPB构造其相应的条件FP-tree;最后采用递归算法分别对这些条件FP-tree进行挖掘,从而得到所有的频繁项集F(Di,min_support).
2) 由频繁项集产生强关联规则
利用上一步得到的频繁项集F(Di,min_support)产生置信度大于等于min_confidence的规则.以频繁项集{ni=T,nj=F}为例,它产生的规则ni=T⟹nj=F,其置信度为
confidence({ni=T}⟹{nj=F})=
(2)
在传统的算法中,如果某一规则的置信度大于等于min_confidence,则该规则为强关联规则.本文改进了传统的算法,将程序中各分支判断语句的静态依赖信息与算法相结合,避免生成无用的强关联规则,使其更适用于B-B相关性的确定,改进后的算法步骤如下:
1) ∀f∈F(Di,min_support),产生f的所有非空子集;
2) 对于f的每一个非空子集g,若规则g⟹(f-g)满足3个条件:
① (f-g)中的元素个数card(f-g)=1;
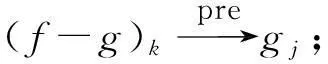
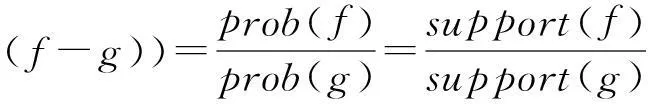
则规则g⟹(f-g)为 “有用的强关联规则”.
下面通过一个例子说明基于关联分析的B-B相关性的确定过程.
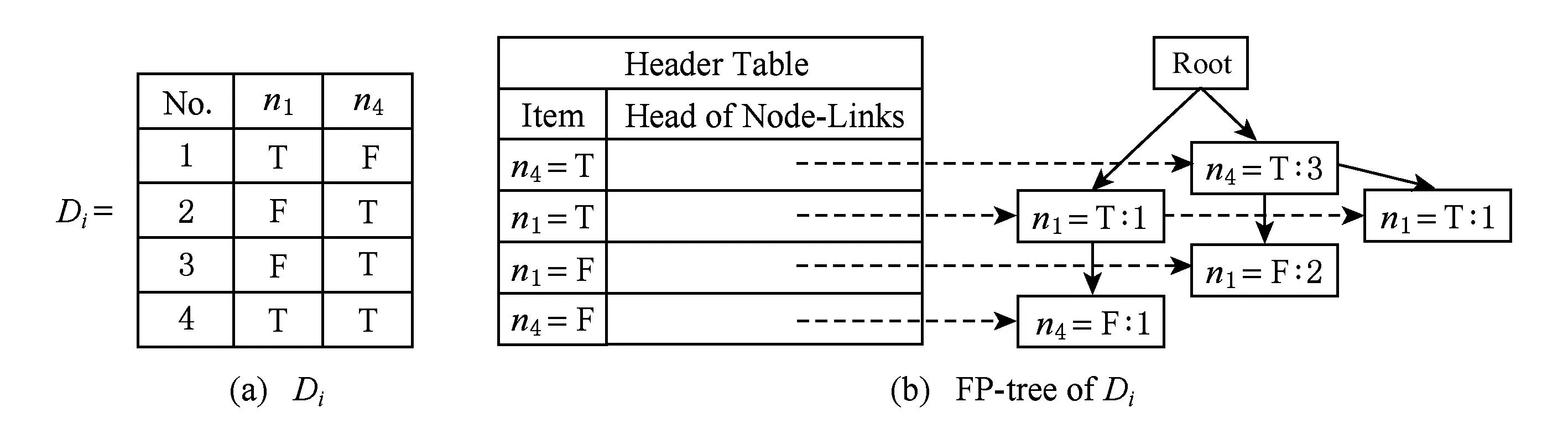
Fig. 3 Diand FP-Tree of Di.图3 Di及其FP-Tree
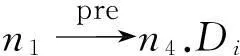
对FP-Tree进行关联分析,可得到支持度大于等于25%的所有频繁项集F(Di,25%),如表1所示:

Table 1 Frequent Itemsets F(Di,25%)
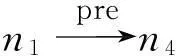
2.3.2基于数据流分析的纯A-B相关性的确定
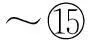
算法2.纯A-B相关性获取算法.
FunctionGetABCorrelation(TP,MTPRT,ARList)
输入:待测程序TP、TP的控制树主干MTPRT、有效强关联规则集ARList;
输出:纯A-B相关性集A-BcorrelationsList.
①A-BcorrelationsList=∅;
②CSList=TP中的所有分支判断语句集合;
③NCSList=ARList中各后项集出现过的分支判断语句集合;
④ for (eachci∈CSList) do
⑤ if (ci∉NCSList) then
⑥referencelocalList=ci引用变量;
⑦ancestorList=MTPRT中ci的祖先;
⑧ intflag=1;
⑨ for (eachrj∈referencelocalList) do
⑩DataFlowAnalysis(rj,ancestorList);


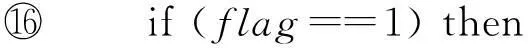

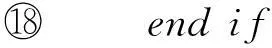
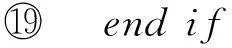


2.4不可达路径的检测
本节根据得到的分支相关性信息确定冲突子路径,从而检测程序中的不可达路径.其中,根据B-B相关性信息确定B-B冲突子路径,根据纯A-B相关性信息确定A-B冲突子路径.
1)B-B冲突子路径的确定.设ni和nj是程序中的2个分支判断语句,如果经过关联分析后得到(ni,nj)有T→T(或T→F)的相关性,则ni(T)→nj(F)(或ni(T)→nj(T))构成B-B冲突子路径;同样,如果(ni,nj)有F→T(或F→F)的相关性,则ni(F)→nj(F)(或ni(F)→nj(T))构成B-B冲突子路径.
2)A-B冲突子路径的确定.设n为分支判断语句,AS为赋值语句集,如果经过数据流分析后得到(AS,n)具有&→T或&→F的相关性,则AS→n(F)或AS→n(T)构成A-B冲突子路径.
在得到的各条B-B冲突子路径中,可能存在着矛盾、冗余或是无用冲突子路径,可根据3个规则进行删减:
规则1. 矛盾冲突子路径删减规则.若ni(T)→nj(T)与ni(T)→nj(F)为2条B-B冲突子路径,且ni与nj同时存在于多个分支节点序列中,则称这2条子路径为矛盾的冲突子路径,并将这2条子路径全部删除;同理,若ni(F)→nj(T)与ni(F)→nj(F)为2条B-B冲突子路径,并且ni与nj同时存在于多个分支节点序列中,应全部删除.
规则2. 冗余冲突子路径删减规则.若ni(F)→nk(F)与ni(F),nj(T)→nk(F)为2条B-B冲突子路径,由于任何可以被后者检测出来的不可达路径同样也可以被前者检测出来,因此称ni(F),nj(T)→nj(F)这类子路径为冗余的冲突子路径,并将其删除.
规则3. 无用冲突子路径删减规则.设ni和nj是2个分支节点,且ni与nj同时存在于多个分支节点序列中,我们将这些序列的集合记为BNS.若在BNS中存在2条分支节点序列a,b,若存在1条B-B冲突子路径ni(T)→nj(T),该冲突子路径可通过分析a得到,并且不能由b得到,则称ni(T)→nj(T)这类子路径为无用的冲突子路径,并将其删除.
确定冲突子路径后,根据不可达路径检测规则检测程序中的不可达路径.
不可达路径检测规则:对于任何一条路径,若该路径包含冲突子路径,则它为不可达路径.
在不可达路径的检测过程中,分支相关性的确定主要依赖于程序中分支节点的执行情况.输入的数据是随机抽取的,因此分支节点的执行情况也带有一定的随机性质.然而,随机数据的抽样规模会影响本文方法的检测效果与效率.如果抽样数据过多,此时采集数据比较全面,因此检测效果较好,但耗时较多;反之如果随机抽取的输入数据过少,此时采集数据不够全面,因此可能产生误报和漏报的情况,检测效果较差,但耗时较少.为了达到较好的平衡点,我们在随机抽样阶段,根据输入数据的可选值域范围,使抽样值的数量足够大,并令采样分布在输入域的各个区域.针对可能会造成抽样不完善的情况,如当一个分支涉及的值域较大而另一个分支涉及的值域较小时,本文采取如下措施进行处理,即针对各个分支判断语句中的条件表达式,通过区间算术方法并结合输入域的边界信息获取分支取值域,尽可能降低因抽样不均衡导致误报、漏报的可能性.
3实验
为了评估本文的方法,首先用一个实例进行了验证,然后选取了5个基准程序和5个开源项目作为测试对象,检测程序中的不可达路径.
3.1实例分析
以程序P′为例来验证本文方法的有效性,图4(a)~4(d)分别为P′的源代码、控制流图及其控制树、蕴含树.
步骤1. 确定B-B相关性.对P′的控制流图、控制树及蕴含树进行搜索,可得到分支节点序列集U={{n3,n4,n5,n14,n17},{ n3,n4,n10,n14,n17}},P′的输入向量为(a,check),在输入域[-350,350]×[T,F]内随机抽样,在此例中,设置抽样值的数目M=128.在抽样值的输入下执行程序,分别得到u1,u2对应的数据集D1,D2,然后分别对D1,D2进行关联分析,可得到表2和表3所示的分析结果.
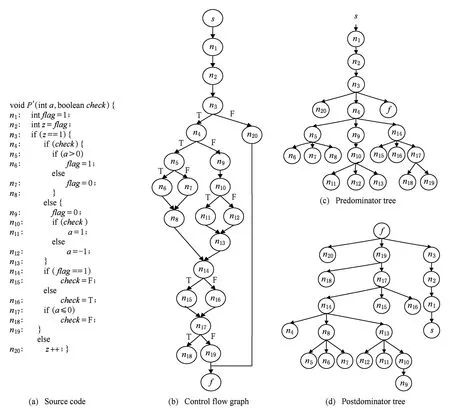
Fig. 4 An example P′.图4 示例P′
步骤2. 确定纯A-B相关性.对未在后项集中出现的分支判断语句n3进行分析,语句n3中的引用变量为z,利用数据流技术分析s→n3间z的定值信息,可得到赋值语句n1和n2使得语句n3中z恒等于1.因此,({n1,n2},n3)具有&→T的A-B相关性.
步骤3. 确定冲突子路径.根据表2及表3中的B-B相关性信息,可得到程序P′中的B-B冲突子路径信息,然后根据冲突子路径的删减规则对B-B冲突子路径进行删减,最终得到如表4所示的B-B冲突子路径.以n5(n6)→n14(n16)为例,其n5和n14是2个分支判断语句,n6为n5的真分支,n16为n14的假分支,因为(n5,n14)有T→T的相关性,所以n5(T)→n14(F)是1条B-B冲突子路径.冲突子路径的删减过程如下:
1) 删除矛盾冲突子路径.因为在u1中(n3,n4)有T→T的相关性,且在u2中(n3,n4)有T→F的相关性,所以n3(T)→n4(F)和n3(T)→n4(T)是2条B-B冲突子路径.由于n3和n4同时存在于u1和u2中,因此这2条子路径为矛盾的冲突子路径,全部删除,其他此类型冲突子路径删除方法相同.
2) 删除冗余冲突子路径.因为在u2中(n3,n10)有T→F的相关性,(n3,n4,n10)有TF→F的相关性,所以n3(T)→n10(T)与n3(T),n4(F)→n10(T)为2条B-B冲突子路径.由于任何可以被n3(T),n4(F)→n10(T)检测出来的不可达路径同样也可以被n3(T)→n10(T)检测出来,因此n3(T),n4(F)→n10(T)为冗余的冲突子路径,将其删除,其他此类型冲突子路径删除方法相同.
3) 删除无用冲突子路径.n14与n17同时存在于u1和u2中,因为在u1中(n14,n17)有T→F的相关性,所以n14(T)→n17(T)是1条B-B冲突子路径.但该冲突子路径不能通过u2得到,因此n14(T)→n17(T)为无用的冲突子路径,将其删除.根据A-B相关性n1,n2→n3(T)可得到n1,n2→n3(n20)是1条A-B冲突子路径,如表5所示.

Table 2 B-B Correlations in u1

Continued (Table 2)

Table 3 B-B Correlations in u2

Table 4 B-B Conflicting Subpaths of P′

Table 5 A-B Conflicting Subpaths of P′
步骤4. 检测不可达路径.根据表4和表5来检测P′中不可达路径,在P′的17条路径中共有14条不可达路径(用pi表示).分别如下:
p1=(s,n1,n2,n3,n4,n5,n6,n8,n14,n15,n17,n18,n19,f);
p2=(s,n1,n2,n3,n4,n5,n6,n8,n14,n16,n17,n18,n19,f);
p3=(s,n1,n2,n3,n4,n5,n6,n8,n14,n16,n17,n19,f);
p4=(s,n1,n2,n3,n4,n5,n7,n8,n14,n15,n17,n18,n19,f);
p5=(s,n1,n2,n3,n4,n5,n7,n8,n14,n15,n17,n19,f);
p6=(s,n1,n2,n3,n4,n5,n7,n8,n14,n16,n17,n19,f);
p7=(s,n1,n2,n3,n4,n9,n10,n11,n13,n14,n15,n17,n18,n19,f);
p8=(s,n1,n2,n3,n4,n9,n10,n11,n13,n14,n15,n17,n19,f);
p9=(s,n1,n2,n3,n4,n9,n10,n11,n13,n14,n16,n17,n18,n19,f);
p10=(s,n1,n2,n3,n4,n9,n10,n11,n13,n14,n16,n17,n19,f);
p11=(s,n1,n2,n3,n4,n9,n10,n12,n13,n14,n15,n17,n18,n19,f);
p12=(s,n1,n2,n3,n4,n9,n10,n12,n13,n14,n15,n17,n19,f);
p13=(s,n1,n2,n3,n4,n9,n10,n12,n13,n14,n16,n17,n19,f).
p14=(s,n1,n2,n3,n20,f).
3.2基准程序实验数据及分析
为了进一步验证本文方法的有效性,实验部分对一组基准程序进行了分析,在保证分支结点被100%覆盖的前提下,最终得到的实验数据如表6所示.表6列出了被测基准程序的信息(1~3列)和不可达路径检测结果(4列).从表6可以看到,本文方法可以检测出各程序中所有的不可达路径.我们通过手动分析来验证实验结果的正确性,经核对,本文方法所检测到的不可达路径均为不可达路径,未发生误报和漏报情况.

Table 6 Experimental Results of Benchmark Programs
3.3开源项目实验数据及分析
利用一组开源程序进行检测,进一步评估本文的方法在复杂程序中检测不可达路径的准确性和性能,这些开源程序可以从SIR(software-artifact infrastructure repository)①下载.这些程序都不是以数值计算为主的程序.其中,NanoXML是一个小型的XML解析器,XML-security为XML数字签名工具,具有较高的代码量和复杂的程序结构.此外,本节将本文的方法与Gong的方法[23]和Suhendra的方法[11]进行了对比.Gong方法利用最大似然估计法获取分支相关性(B-B相关性)信息,进而实现不可达路径的检测;Suhendra方法使用静态分支相关性分析方法,通过检查赋值语句和分支判断语句之间、不同分支判断语句之间是否存在冲突来检测程序中的不可达路径.表7中列出了被测程序的信息,表8为对开源程序的不可达路径检测结果.其中,表8的第2列为总路径数.基于程序控制流图分析,先计算普通分支或嵌套分支结构对应的路径数,然后根据各部分间的连接方式(如串接等)计算程序的总路径数;第3列为不可达路径数.通过本文方法检测到的不可达路径数与人工分析得到的不可达路径数进行对比.本文的一位作者与 2名大学四年级学生花费近2个月时间,手动分析来评估试验结果的正确性,借助Soot,GraphViz②等工具对程序的数据依赖、调用依赖关系等信息进行可视化处理,一定程度上降低了手动分析的工作量.图5和图6分别从分支节点覆盖率和检测精度2个方面将本文的方法与其他 2种方法进行了比较.
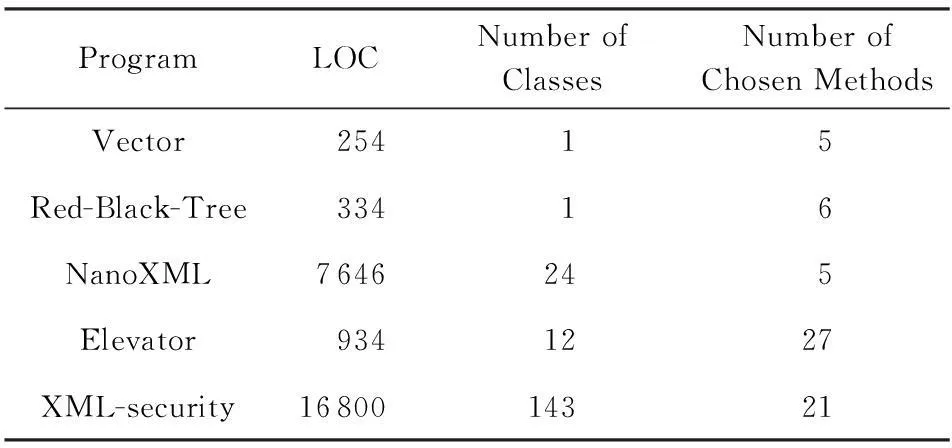
Table 7 Descriptions of Industry Programs
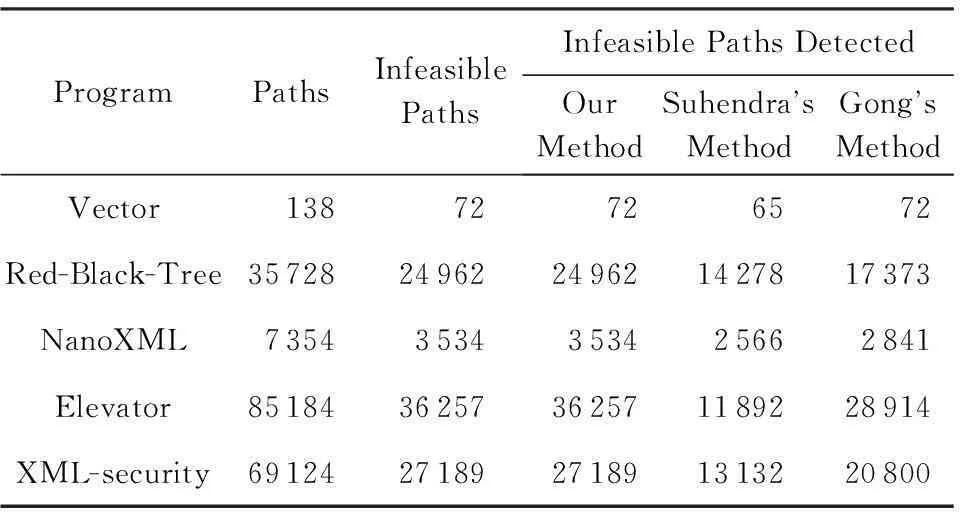
Table 8 Comparison of Results of SIR’s Programs
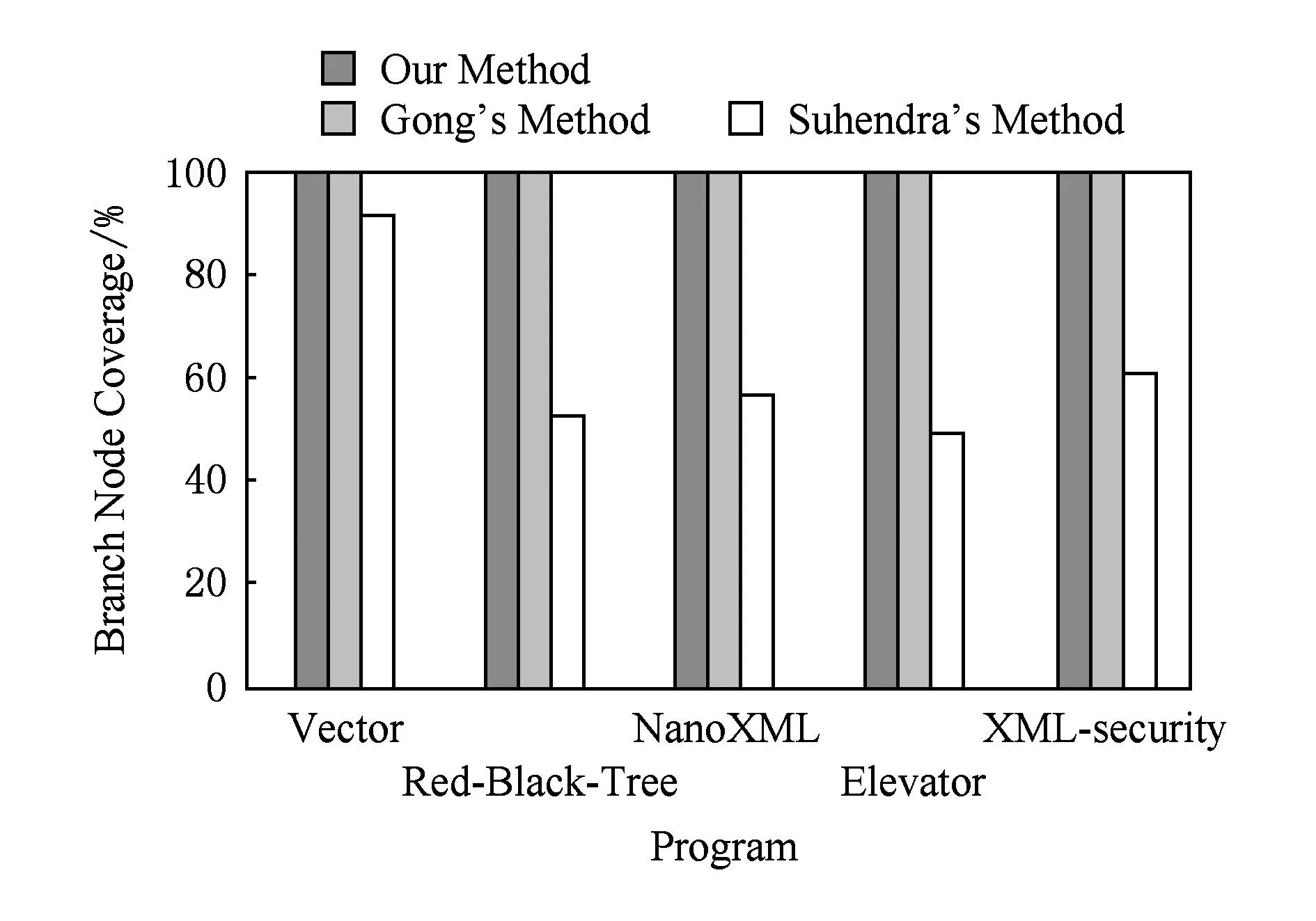
Fig. 5 Comparison of branch node coverage of three methods.图5 分支节点覆盖率比较
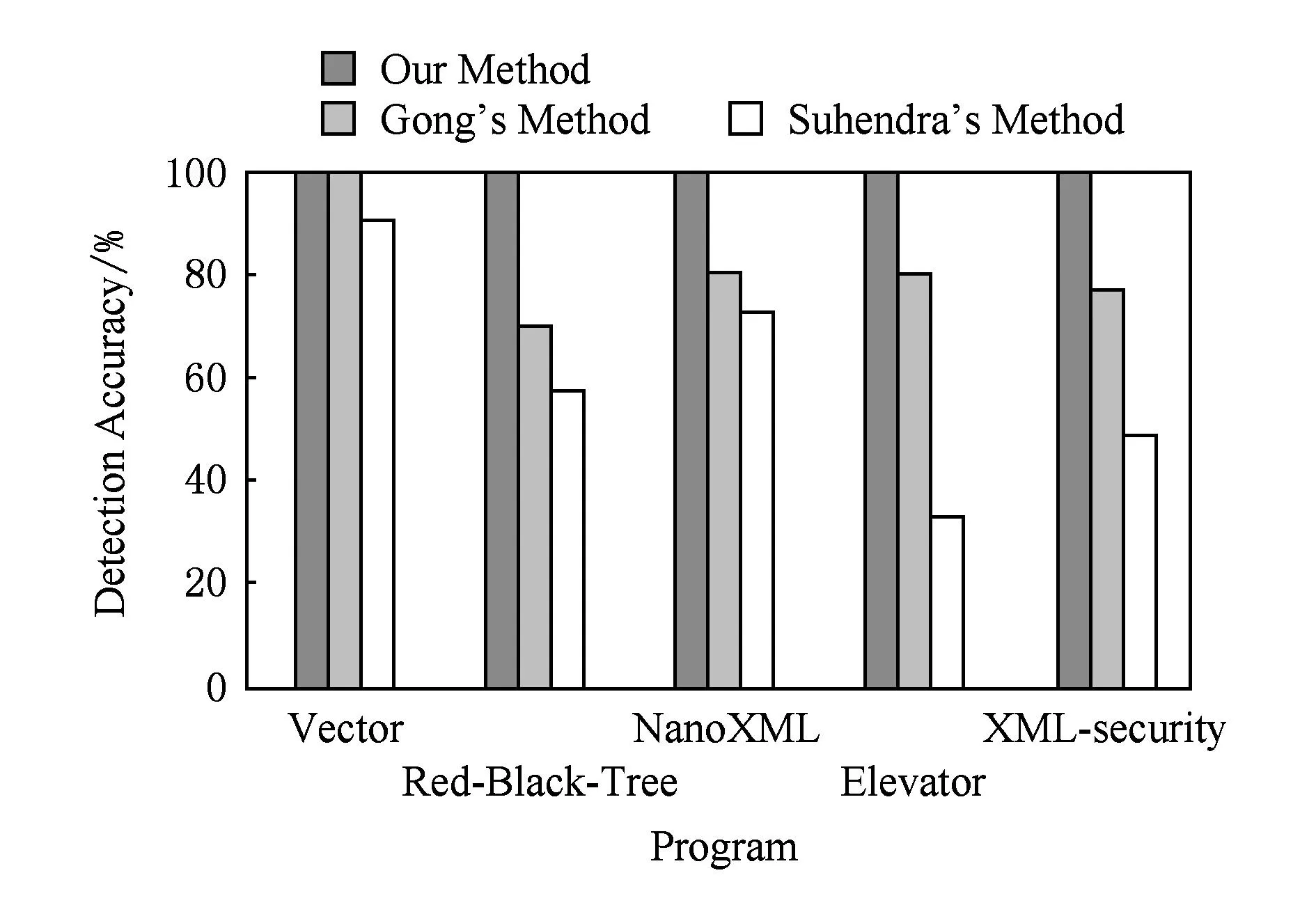
Fig. 6 Comparison of detection accuracy of three methods.图6 检测精度比较
从表8、图5和图6可以看到,本文方法可以检测出程序中所有不可达路径.而Suhendra方法由于在分析赋值语句对分支判断语句的影响时,仅能分析对变量直接进行常量赋值的赋值语句,且该方法不能很好地处理带有循环等结构的程序.因此该方法只能检测出程序中的部分不可达路径,分支节点覆盖率和检测精度较低.特别是在分析程序Elevator时,Suhendra方法检测精度仅有32.8%.Gong方法分支节点覆盖率较高,但是由于该方法没有对A-B相关性进行分析,且在分析B-B相关性时,该方法需要对具有B-B相关性的分支判断语句的个数的最大值进行限定,无法检测到由多于限定值的分支判断语句间B-B相关性而引起的不可达路径.因此,在检测精度方面,Gong方法相对于本文方法较低.
综上所述,不管是对基准程序还是开源项目,本文方法在不可达路径检测方面都有较好效果,可以准确地检测出被测程序中的不可达路径.当分支节点覆盖率小于100%时,本文方法可能产生误报和漏报.我们在随机抽样阶段已采取措施将此可能性降到最低.在2组实验中,本文方法均未出现误报和漏报情况.在时间复杂度方面,假设待测程序的语句条数为N,本文方法的时间复杂度为O(4N2),Gong方法的复杂度为O(3N2),Suhendra方法的时间复杂度为O(2N2),本文的方法在时间复杂度方面较其他2种方法稍有增加,但总体上仍属于同一个数量级.可见,本文方法是一种有效的检测程序中不可达路径的方法,可有效地提高软件测试的效率.
4相关工作
目前,很多学者针对不可达路径检测开展广泛研究,提出了若干解决方法.常见的方法主要有静态检测方法和动态检测方法2类:
1) 静态检测方法可分为基于路径条件可满足性的检测方法和基于分支相关性检测方法.在路径条件可满足性分析方面,文献[3-5]使用方程组来表示各条路径,通过判断方程组是否有解来判定路径的可达性.然而,这类方法的复杂度较高,而且在处理带有数组、指针等结构的程序时,不能很好地工作;文献[6-7]将区间算术用于判断路径的可达性,但是该类方法不能很好地解决条件谓词中包含非线性表达式的情况;Ding等人[8]使用符号执行技术对符合代码模式的分支进行分析,进而实现不可达路径的检测;肖庆等人[9]使用变量的抽象取值范围来表示属性状态条件,通过判断属性状态条件中的变量取值范围是否为空来判断路径的可达性.在分支相关性的分析方面,Bodik等人[10]在传统的数据流分析中加入了分支相关性分析,从而提高传统数据流分析的精度;Suhendra等人[11]通过检查赋值语句和分支语句之间、不同分支语句之间是否存在冲突来检测不可达路径.然而,该方法在分析赋值语句对分支语句的影响时,仅能分析对变量直接进行常量赋值的赋值语句,且该方法不能很好地处理带有循环等结构的程序;Burhan等人[12]使用静态分析技术对程序的控制流和数据流进行分析,确定存在相关性的语句,进而检测不可达路径;Frank[13]对传统的数据流分析算法进行了改进,并将其用于面向对象程序的不可达路径检测;Mu等人[14]提出了一种面向函数调用关系的不可达路径检测算法,通过分析程序的控制流和数据流信息获取条件分支相关性信息,从而实现面向函数的不可达路径的检测.在静态检测方法中,基于路径条件可满足性的检测方法复杂度较高,而基于分支相关性的检测方法分支节点覆盖率较低.本文提出了一种基于分支相关性分析、动静态结合的不可达路径检测方法,通过关联分析和数据流分析获取分支相关性信息,提高了不可达路径的检测精度,并有效克服了使用纯静态分支相关性分析方法分支节点覆盖率低的问题,能有效处理带有复杂谓词表达式的程序.
2) 动态检测方法通常是在对目标路径生成测试数据阶段来判定路径的可达性.Balakrishnan等人[15]提出了一种语义更新技术,它能从语义上自动排除程序中的不可达路径.文献[16-17]利用遗传算法来检测不可达路径,为了更好地引导搜索,该类方法通过结合控制流图进行适应度函数的设计.然而,该类方法的计算代价较大.本文方法利用JDI获取分支判断语句的执行信息,并在此基础上采用关联分析技术确定分支的相关性信息,降低了计算代价.
除以上2类主要方法外,研究人员还提出一些动静态结合的不可达路径检测方法.Yang等人[24]首先使用静态数据流分析方法评估路径的可达性,路径中定义使用对惩罚值之和越低表示路径的可达性越高,然后根据评估值移除路径集中的不可达路径,最后针对静态方法未检测到的不可达路径,在测试数据生成阶段利用基于元启发式动态分析技术进行检测.Gong等人[23]首先通过最大似然估计法计算分支判断语句不同输出结果的条件分布概率值,确定分支相关性(B-B相关性),然后根据分支相关性检测不可达路径.与本文方法不同的是:1)Gong方法没有分析A-B相关性信息,无法检测到仅由纯A-B相关性引起(不是由B-B相关性引起)的不可达路径;2)在对开源项目进行不可达路径检测时,该方法对具有B-B相关性的分支判断语句数的最大值进行了限定,无法检测到由多于限定值的分支判断语句间的B-B相关性而引起的不可达路径,而本文的方法无需此约束即可检测由任意分支判断语句间B-B相关性引起的不可达路径,从而具备更强的适用性.
本文方法利用关联分析和数据流分析技术对引起分支相关性的情况进行全面的分析,具有较强的不可达路径检测能力和较高的检测精度,可以准确地检测出被测程序中的不可达路径.综上所述,本文方法是一种有效的不可达路径检测方法,可以有效地提高软件测试的效率.
5结论与进一步工作
本文提出了一种新的不可达路径检测方法,首先构建反映各分支判断语句静态依赖关系和动态执行信息数据集;然后利用关联分析方法获取B-B相关性信息,在此基础上利用静态数据流分析技术获取纯A-B相关性信息,提高了不可达路径的检测精度;最后根据分支相关性检测不可达路径.通过实验与分析,本文方法能够准确地检测出程序中的不可达路径,进而可以有效地提高软件测试的效率.
未来还有几个方面的问题需要深入研究:如针对本文的方法还需要进行大量的实验进行验证;进一步完善我们的原型工具,为后续的路径测试提供有价值的信息.此外,对关联分析方法进一步的改进和优化,使其更适用于B-B分支相关性的确定;如何缩减冗余的强关联规则也是我们未来研究方向之一.
参考文献
[1]Shan Jinhui, Jiang Ying, Sun Ping. The progress of testing research[J]. Journal of Beijing University, 2005, 41(1): 134-145 (in Chinese)(单锦辉, 姜瑛, 孙萍. 软件测试研究进展[J]. 北京大学学报, 2005, 41(1): 134-145)
[2]Hedley D, Hennell M A. The causes and effects of infeasible paths in computer programs[C]Proc of the 8th Int Conf on Software Engineering. New York: ACM, 1985: 259-266
[3]Coward P D. Symbolic execution and testing[J]. Information and Software Technology, 1991, 33(1): 53-64
[4]Goldberg A, Wang T C, Zimmerman D. Applications of feasible path analysis to program testing[C]Proc of the 1994 Int Symp on Software Testing and Analysis. New York: ACM, 1994: 80-94
[5]Cadar C, Dunbar D, Engler D. KLEE: Unassisted and automatic generation of high-coverage tests for complex systems programs[C]Proc of the 8th USENIX Conf on Operating Systems Design and Implementation. Berkeley: USENIX Association, 2008: 209-224
[6]Wang Silan, Wang Yawen, Gong Yunzhan. Path chooses based on interval arithmetic for unit coverage testing[J]. Journal of Tsinghua University, 2011, 51(S1): 1402-1406 (in Chinese)(王思岚, 王雅文, 宫云战. 单元覆盖测试中基于区间运算的路径选择[J]. 清华大学学报, 2011, 51(S1): 1402-1406)
[7]Wang Zhiyan, Liu Chunnian. Applications of interval arithmetic to software testing[J]. Journal of Software, 1998, 9(6): 438-443 (in Chinese)(王志言, 刘椿年. 区间算术在软件测试中的应用[J]. 软件学报, 1998, 9(6): 438-443)
[8]Ding S, Zhang H Y, Tan H B K. Detecting infeasible branches based on code patterns[C]Proc of the CSMR-WCRE Conf on Software Maintenance, Reengineering and Reverse Engineering. Piscataway, NJ: IEEE, 2014: 74-83
[9]Xiao Qing, Gong Yunzhan, Yang Zhaohong, et al. Path sensitive static defect detecting method[J]. Journal of Software, 2010, 21(2): 209-217 (in Chinese)(肖庆, 宫云战, 杨朝红, 等. 一种路径敏感的静态缺陷检测方法[J]. 软件学报, 2010, 21(2): 209-217)
[10]Bodik R, Gupta R, Soffa M L. Refining data flow information using infeasible paths[C]Proc of the 6th European Software Engineering Conf and the 5th ACM SIGSOFT Symp on the Foundations of Software Engineering. New York: ACM, 1997: 361-377
[11]Suhendra V, Mitra T, Roychoudhury A, et al. Efficient detection and exploitation of infeasible paths for software timing analysis[C]Proc of the IEEEACM Design Automation Conf. New York: ACM, 2006: 358-363
[12]Burhan B, Izzat A. Infeasible paths detection using static analysis[J]. The Research Bulletin of Jordan ACM, 2013, 2(3): 120-126
[13]Frank T. Infeasible paths in object-oriented programs[J]. Science of Computer Programming, 2015, 97(P1): 91-97
[14]Mu Yongmin, Zheng Yuhui, Zhang Zhihua, et al. The algorithm of infeasible paths extraction oriented the function calling relationship[J]. Chinese Journal of Electronics, 2012, 21(2): 236-240
[16]Bueno P M S, Jino M. Identification of potentially infeasible program paths by monitoring the search for test data[C]Proc of the 15th IEEE Int Automated Software Engineering Conf. Piscataway, NJ: IEEE, 2000: 209-218
[17]Goldberg D E. Genetic Algorithms in Search, Optimization and Machine Learning[M]. New York: Addison-Wesley, 1989
[18]Chen Rui. Infeasible path identification and its application in structural test[D]. Beijing: Institute of Computing Technology, Chinese Academy of Sciences, 2006 (in Chinese)(陈蕊. 程序中不可达路径的识别及其在结构测试中的应用[D]. 北京: 中国科学院计算技术研究所, 2006)
[19]Agrawal H. Dominators, super blocks, and program coverage[C]Proc of the 21st Annual ACM SIGPLAN-SIGACT Symp on Principles of Programming Languages. New York: ACM, 1994: 25-34
[20]Mao Chengying, Lu Yansheng. A simplified method for generating test path cases in branch testing[J]. Journal of Computer Research and Development, 2006, 43(2): 321-328 (in Chinese)(毛澄映, 卢炎生. 分支测试中测试路径用例的简化生成方法[J]. 计算机研究与发展, 2006, 43(2): 321-328)
[21]Shen Bin. Research on the technologies of association rules[D]. Hangzhou: Zhejiang University, 2007 (in Chinese)(沈斌. 关联规则相关技术研究[D]. 杭州: 浙江大学, 2007)
[22]Han Jiawei, Pei Jian, Yin Yiwen. Mining frequent patterns without candidate generation[C]Proc of the 2000 ACM SIGMOD Int Conf on Management of Data. New York: ACM, 2000: 1-12
[23]Gong Dunwei, Yao Xiangjuan. Automatic detection of infeasible paths in software testing[J]. IET Software, 2010, 4(5): 361-370
[24]Yang Rui, Chen Zhenyu, Xu Baowen, et al. Improve the effectiveness of test case generation on EFSM via automatic path feasibility analysis[C]Proc of the 13th IEEE Int High Assurance Systems Engineering Symp. Piscataway, NJ: IEEE, 2011: 17-24

Jiang Shujuan, born in 1966. Professor and PhD supervisor. Member of China Computer Federation. Her research interests include compilation techniques and software engineering.

Han Han, born in 1989. Master. Her research interests include program analysis and software testing (hhan@cumt.edu.cn).

Shi Jiaojiao, born in 1988. Master. Her research interests include program analysis and software testing (sjiao888@126.com).

Zhang Yanmei, born in 1982. PhD and lecturer. Her research interests include program analysis and software testing (ymzhang@cumt.edu.cn).

Ju Xiaolin, born in 1976. PhD and associate professor. His research interests include program analysis and software testing (XiaolinJu@gmail.edu.cn).

Qian Junyan, born in 1973. PhD and professor. Member of China Computer Federation. His research interests include software engineering, model checking and program verification (qjy2000@guet.edu.cn).
Detecting Infeasible Paths Based on Branch Correlations Analysis
Jiang Shujuan1,4, Han Han1, Shi Jiaojiao1, Zhang Yanmei1,2, Ju Xiaolin1,3, and Qian Junyan4
1(SchoolofComputerScienceandTechnology,ChinaUniversityofMiningandTechnology,Xuzhou,Jiangsu221116)2(StateKeyLaboratoryforNovelSoftwareTechnology(NanjingUniversity),Nanjing210023)3(SchoolofComputerScienceandTechnology,NantongUniversity,Nantong,Jiangsu226019)4(GuangxiKeyLaboratoryofTrustedSoftware(GuilinUniversityofElectronicTechnology),Guilin,Guangxi541004)
AbstractThe existence of infeasible paths causes a waste of test resources in software testing. Detecting these infeasible paths effectively can save test resources and improve test efficiency. Since the correlation of different conditional statements is the main reason of causing infeasible paths of a program and it costs effort for attempting to cover these paths which are never executed during software testing, the determination of branch correlations plays an important role in detecting infeasible paths. The paper proposes a new approach for detecting the infeasible paths based on association analysis and data flow analysis. Firstly, it builds the data-sets that reflect the static dependencies and the dynamic execution information of conditional statements by combining static analysis with dynamic analysis; then, with two types of branch correlations (called A-B correlation and B-B correlation) defined, it determines the branch correlations respectively with two introduced algorithms which are based on association analysis and data flow analysis; finally, it detects the infeasible paths in accordance with the obtained and refined branch correlations. The paper applies the proposed approach to some benchmarks programs and industry programs to validate its efficiency and effectiveness. The experimental results indicate that our approach can detect infeasible paths accurately and improve the efficiency of software testing.
Key wordssoftware testing; infeasible paths; branch correlations; association analysis; data flow analysis
收稿日期:2014-09-15;修回日期:2015-10-09
基金项目:国家自然科学基金项目(61502497,61562015);计算机软件新技术国家重点实验室(南京大学)基金项目(KFKT2014B19);广西可信软件重点实验室(桂林电子科技大学)研究课题(kx201530);南通市应用研究计划基金项目(BK2014055)
中图法分类号TP311
This work was supported by the National Natural Science Foundation of China (61502497,61562015), the Foundation of State Key Laboratory for Novel Software Technology (Nanjing University) (KFKT2014B19), the Foundation of Guangxi Key Laboratory of Trusted Software (Guilin University of Electronic Technology) (kx201530), and the Nantong Application Research Plan Foundation (BK2014055).
