基于求解开销预测的符号执行搜索策略研究
2016-06-16刘经德陈振邦
刘经德 陈振邦 王 戟,2
1(国防科学技术大学计算机学院 长沙 410073)2(并行与分布处理国防科技重点实验室(国防科学技术大学计算机学院) 长沙 410073)3(95835部队 新疆巴音郭楞 841700)(liujingde@nudt.edu.cn)
基于求解开销预测的符号执行搜索策略研究
刘经德1,3陈振邦1王戟1,2
1(国防科学技术大学计算机学院长沙410073)2(并行与分布处理国防科技重点实验室(国防科学技术大学计算机学院)长沙410073)3(95835部队新疆巴音郭楞841700)(liujingde@nudt.edu.cn)
摘要符号执行中约束求解所占的时间比例非常高.同时,不同复杂度约束的求解时间开销差距悬殊,这一现象在对包含复杂数值计算的程序进行符号执行时尤为明显.在指定时间内求解更多约束有利于覆盖更多语句和探索更多路径.为此,提出了基于求解开销预测的符号执行搜索策略.基于实验总结出了度量约束复杂度的经验公式,并结合约束的历史求解开销来预测当前的求解开销,从而在符号执行过程中优先探索求解开销较小的路径.在KLEE中实现了上述搜索策略,并对GNU科学计算库(GSL)中的12个模块进行了实验.实验结果表明,相比现有搜索策略,提出的搜索策略在保证语句覆盖率的同时,可以探索更多的路径(平均24.34%提高);而且,在相同时间内,可以查找出更多的软件缺陷,同时查找出相同缺陷的时间开销平均降低了44.43%.
关键词符号执行;约束求解;加权随机搜索;缺陷查找;语句覆盖
符号执行是一种相对精确的程序分析技术[1],由King[2]于1976年提出.符号执行可以系统地遍历程序的路径空间;现阶段符号执行技术主要用于软件测试[3]、查找程序缺陷[4]和程序验证[5].
在程序符号执行过程中,路径空间随着程序中分支语句的数量增加呈指数级增长;同时,某些程序的路径空间还可能是无穷的.因此,符号执行面临根本性的路径爆炸问题,如何在有限时间内更加高效地探索程序路径空间成为了研究的热点.1)符号执行中的通用搜索策略希望在有限资源内覆盖更多的程序语句或路径,包括深度优先搜索(depth-first search, DFS)、随机状态搜索(random state search, RSS)、随机路径搜索(random path search, RPS)以及覆盖率优化搜索(coverage-optimized search, COS)等;2)也有一些工作针对某个具体目标研究高效的路径空间搜索策略,包括提高程序语句覆盖率[6]、面向可达性的搜索策略[7]、面向程序不同版本差异的搜索策略[8]等.
然而,符号执行中现有搜索策略在约束求解方面的考虑不够,而符号执行中很大一部分时间开销花在约束求解上.例如使用符号执行工具KLEE[4]对Coreutils中的89个程序进行符号执行,其中求解时间占总时间的41%[4].同时,由于程序中不同路径的路径条件(path condition, PC)复杂度的差别可能很大,从而导致其求解开销相差悬殊,使得小部分路径的求解可能在符号执行中占用了大部分的求解时间.对于包含复杂数值运算的程序,比如科学计算程序,由于涉及不同规模的线性及非线性运算,其中的约束求解开销相差非常悬殊,从而造成的上述特征更为明显.现有的符号执行搜索策略在进行路径选择时都没有考虑到这一点,导致符号执行在分析复杂运算程序时无法在有限的时间内探索更多的程序路径,从而制约了符号执行探索路径空间的能力.
针对这个问题,本文提出了一种基于求解开销预测的符号执行搜索(solving cost predication based search, SCPS)策略,通过对符号执行中的求解开销进行经验预测,在兼顾程序语句覆盖率的前提下,优先选择求解开销小的路径进行探索,从而可在有限时间内提高探索路径的数量.本文在开源符号执行器KLEE上实现了SCPS,并在开源程序上开展了实验,实验结果表明:在指定时间内,和已有搜索策略相比,本文提出的SCPS可在保持语句覆盖率的同时探索更多路径,查找出更多缺陷,并能够在查找相同缺陷时需要更少的时间.
1背景介绍及示例
1.1符号执行简介
在符号执行中,用符号值作为被分析程序的输入,程序状态中包含3个信息:1)变量的符号值或实际值;2)当前的路径条件;3)程序计数器.
图1是一个简单的示例程序.函数foo()含有2个整型变量参数x和y.对foo()函数进行符号执行过程如图2所示.程序的初始状态为state0,其中X和Y表示变量x和y的符号值,其路径条件为true,表示没有任何约束.当符号执行到行②if (x>0)时,由于为分支语句,这时会对路径进行分叉生成2条路径,分别对应if (x>0)的真分支和假分支.在这2条不同的路径上,相应的分支条件会加到所对应路径的路径条件中,然后调用求解器来判断新的分支条件是否可满足,以判断路径的可行性.图2中左边路径的当前状态用state1表示,其路径条件为X>0;右边路径的当前状态用state2表示,其路径条件为X≤0.这2条路径都存在使相应路径条件为真的X和Y的取值,所以这2条路径都可行.在接下来的执行中,2条路径分别执行if语句对应的then块和else块,然后进行符号运算,变量y的取值最后分别为Y-X和Y+X.

Fig. 1The first program.
图1示例程序1
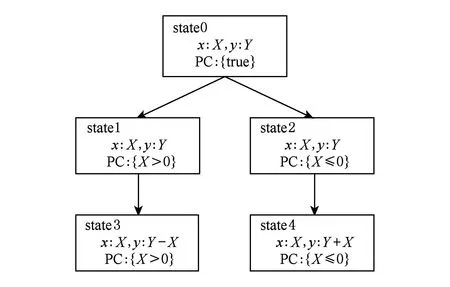
Fig. 2 The execution tree of the first program.图2 示例程序1的执行树
从上述介绍可知,符号执行会生成被分析程序的路径树,树中每个结点表示一个状态,每个叶结点都对应程序一条抽象路径,表示满足此路径相应路径约束的输入会使程序执行这条路径.因此,符号执行的过程也是对程序路径树的探索过程.一般而言,符号执行的核心过程是一个由状态选择、指令执行、状态更新3部分构成的循环,其基本过程如下:1)从初始状态开始,所有未探索的状态构成一个候选状态集合;2)循环首先根据指定的搜索策略从候选状态集合中选择一个状态;3)执行这个状态中程序计数器所指向的指令,在执行指令过程中如果需要判断路径可行性则对该路径的路径条件进行求解,在执行分支指令时可能会加入新的状态;4)更新状态信息,有时根据需要其他状态的信息也将被更新.状态选择决定了符号执行探索路径空间的方式,通常的探索方式有DFS,RSS,RPS,COS等.同时,也可采用不同策略的组合,以同时发挥不同策略的特点.例如,符号执行工具KLEE实现了10种搜索策略,并默认使用RPS+COS的策略组合.
1.2基于求解开销预测的搜索策略示例
下面用1个例子介绍本文提出的SCPS搜索策略.
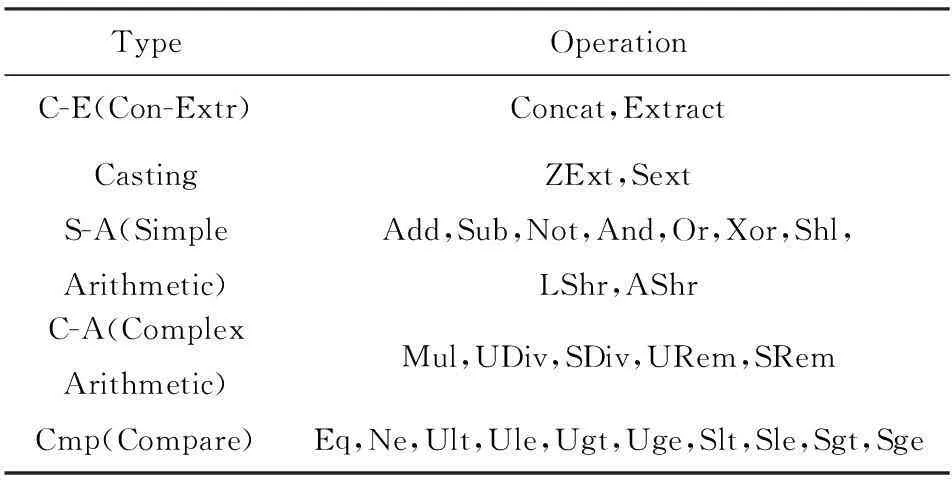
图3中的程序,target的初始值为0,在每次执行断言“assert(target<2)”前都会执行一次“target++”操作,可以发现在第2次执行“assert(target<2)”时出现断言违例错误.该程序的执行树如图4所示,图4中有5个状态执行了“assert(target<2)”语句,分别为:state4,state5,state7,state9和state11.为突出比较就本示例而言不同搜索策略在缺陷查找方面的能力,现忽略和触发断言违例无关的状态,仅考虑选择上述5个状态中的哪2个去触发断言违例开销最小,即耗时最短.通过实验我们统计了使用STP[9]对上述5个状态的PC进行求解的求解时间(solving time, ST),求解时间按大小排序如下:

Fig. 3The second program.
图3示例程序2
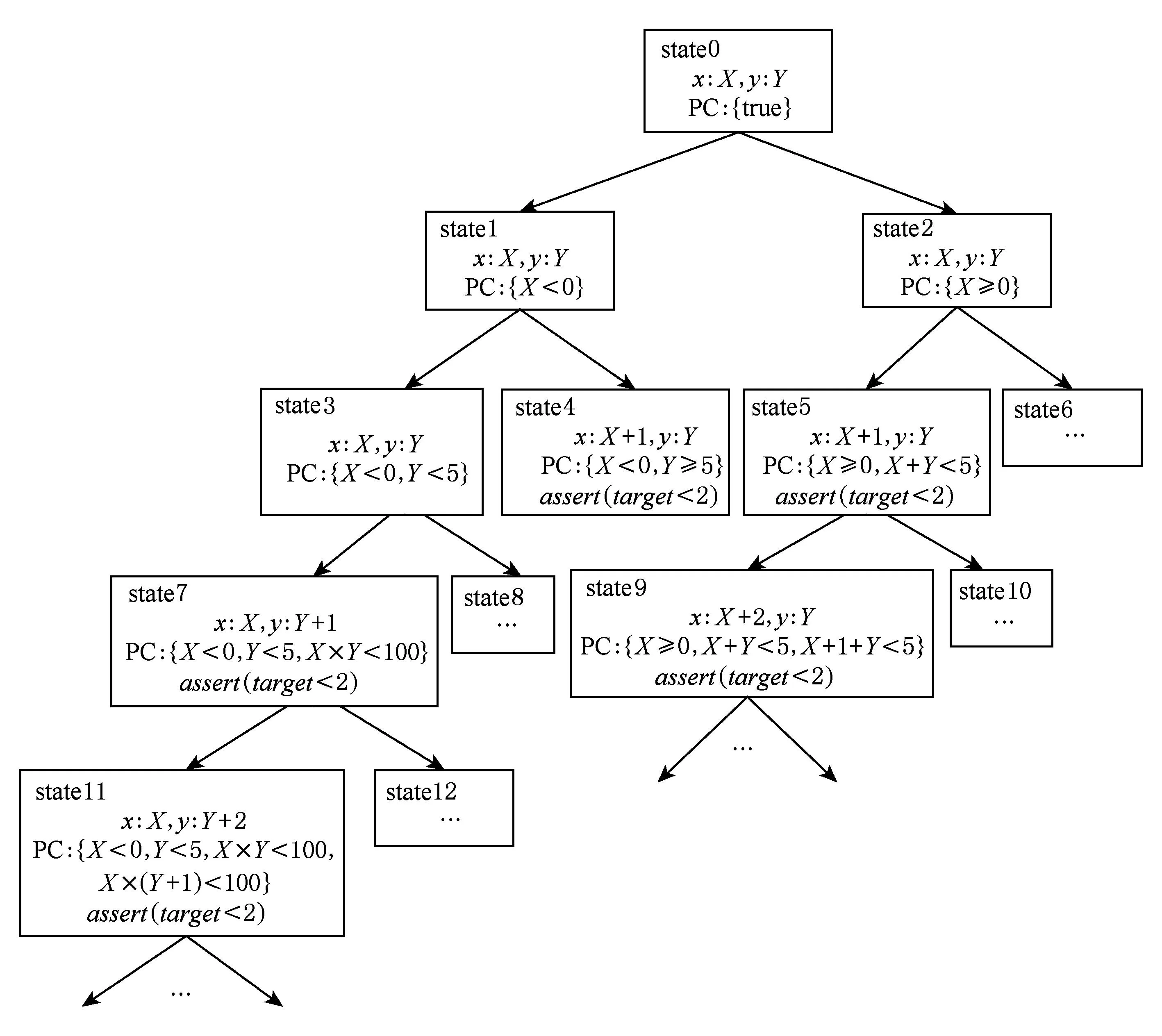
Fig. 4 The execution tree of the second program.图4 示例程序2的执行树
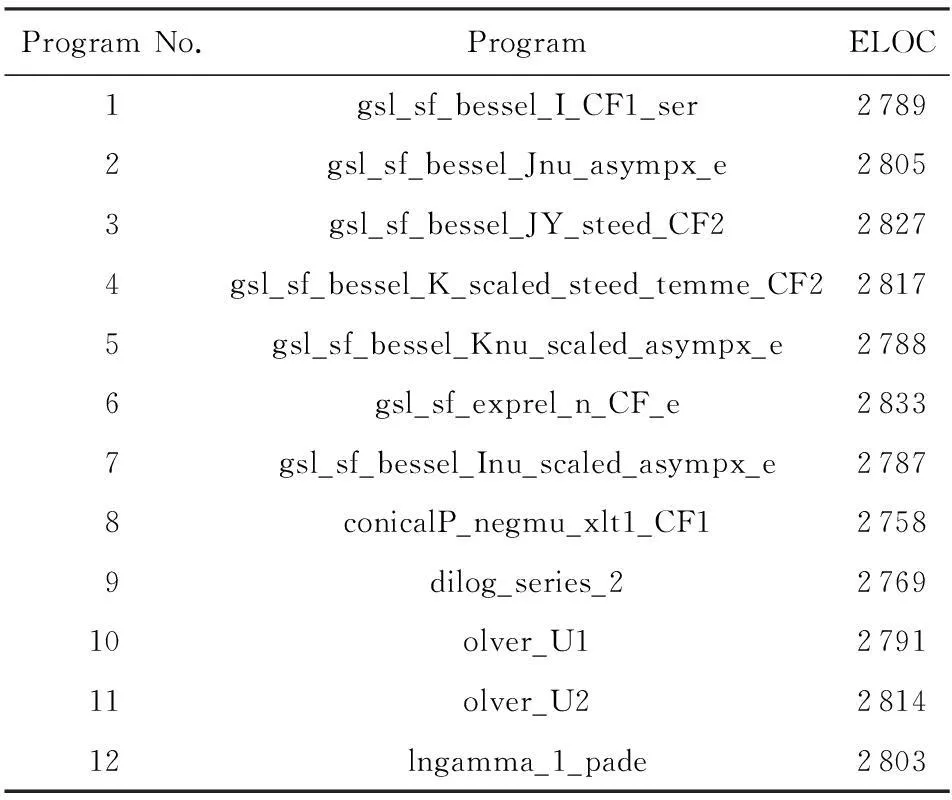
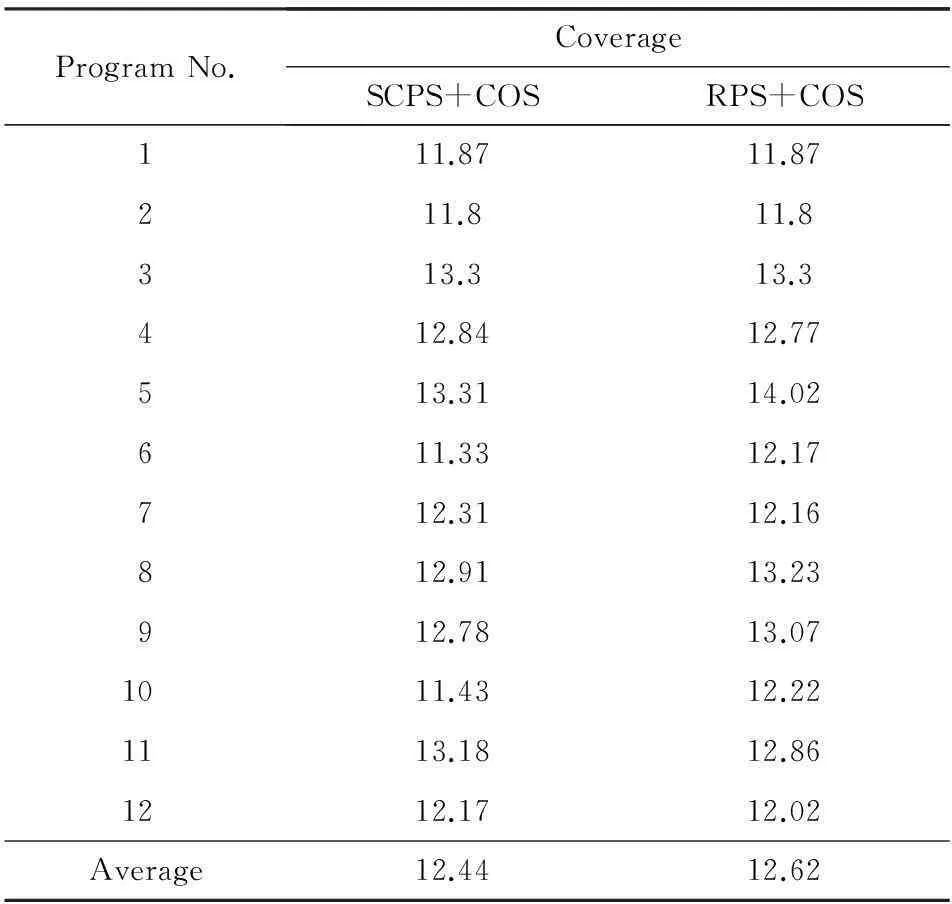
ST{X<0,Y≥5} ST{X<0,Y<5,X×Y<100,X×(Y+1)<100}. 触发断言违例的状态组合有5种: ①〈state4,state7〉;②〈state4,state5〉;③〈state5,state7〉;④〈state5,state9〉;⑤〈state7,state11〉.理想情况下这5种组合的求解时间开销按大小排序为:ST2 2基于求解开销预测的加权随机搜索策略 2.1基于约束复杂度的求解开销预测 在符号执行中,每条路径的PC形如C1∧C2∧…∧Ci∧…∧Cn,其中Ci(1≤i≤n)表示一个分支条件.分支条件是一些常量和变量的表达式,其中的运算和操作主要包括:位操作、字符串操作、数值运算和比较操作等.PC的复杂度和其表达式长度、包含运算类型以及运算中所涉及的变量和常量中的数据个数等因素有关. 针对同一约束条件进行求解,不同求解器的求解开销不一样.对于同一个求解器,不同约束的求解开销也可能相差悬殊;同时,由于求解器的能力有限,有些复杂的约束(比如包含复杂的高阶运算)甚至求解器无法及时地得到结果.虽然对约束进行求解前我们无法预知其准确的求解开销,但约束的求解开销与约束复杂度具有直接的联系;因此,通过评估约束的复杂度,可以对约束的求解开销进行预测.为了评估约束的复杂度,根据不同操作的复杂性,我们将PC中涉及的操作进行了分类,如表1所示.其中,C-E是字符串操作类,Casting是位扩展操作类,S-A是简单的算术运算、逻辑运算及位操作类,C-A是复杂的算术运算类,Cmp是比较操作类. 另外,PC中常量和变量的个数分别用NCon和NVar表示,PC中操作类型A中所包含的操作出现的次数为NA.例如C-E类型中所包含的操作个数记为NC-E.为通过收集实验数据总结约束求解开销的经验公式,我们使用KLEE对GNU Scientific Library (GSL)[10]中的gsl_sf_bessel_I_CF1_ser和conicalP_negmu_xlt1_CF1这2个模块进行了符号执行,并在执行时记录了所有约束的逻辑表达式及对其求解的时间开销,然后从这2个模块的求解记录中各随机选取15条未被KLEE中的求解优化方法命中的约束,对每条约束的逻辑表达式进行解析,统计出各表达式中不同操作类型的操作出现次数、不同操作数出现次数以及变量和常量的个数,最后使用多元线性回归分析方法对30组数据进行分析,最终得到约束求解复杂度的经验公式: Table 1 The Operation Type in Logical Expressions (1) 另一方面,因为当前路径的历史求解开销总和比上历史PC复杂度总和反映了在该路径上单位复杂度所对应的求解开销均值,为了提高求解开销预测的准确性,可以用历史单位复杂度的求解开销均值乘以当前的求解复杂度来预测其求解开销. 假设当前状态对应所在路径的第n+1个结点,其路径条件PCn+1的逻辑表达式为C1∧C2∧…∧Ci∧…∧Cn∧Cn+1,(1≤i≤n).在当前路径的第i个结点处的路径条件PCi的约束复杂度记为Si,求解实际开销记为Ti,则PCn+1的求解开销预测值PTn+1可表示为 (2) 2.2加权随机搜索 在进行状态选择时,如果严格选择所有候选状态中PC求解开销预测值最小的进行执行,将可能使符号执行局限于某些简单的循环中,并且在每次进行状态选择时都会带来较大的选择开销.为了在优先选择求解开销更小的状态的同时,提高符号执行对程序的覆盖率,我们参考KLEE中实现的加权随机搜索(weighted random search)算法,对基于求解开销预测的搜索策略进行优化.通过优化降低了状态选择开销,并提高了语句覆盖率. 根据PC的求解开销预测值PT对相应状态赋予一个权值weight(记为W),PT越大,W越小,即在状态选择中被选择的概率越小.对于求解开销预测值在1 s内的我们将其权值统一设为1,对于预测值超过最大求解时间TMST(max solving time, MST),我们也将它们的权值设为相同,这样有助于避免某些状态“饿死”.W与PT的对应关系如下: (3) 加权随机搜索算法该使用一棵二叉执行树维护当前所有候选状态的信息,叶结点就是候选状态,内部结点就是路径分叉点,路径分叉点处的W值为0,它还记录了以该结点为根结点的二叉树的所有叶结点的权值之和Wsum,算法1描述了加权随机搜索算法.该算法的核心思想是首先产生一个(0,1]的随机数p,从左往右累加二叉树各叶结点的W值,直到加上某个叶结点的W值之前累加之和小于p×Wsum,而加上该叶结点的W值之后累加之和大于或等于p×Wsum时,则结束搜索,选择该叶结点对应的state. 算法1. 加权随机搜索算法. 输入:记录所有当前候选状态信息的二叉树,(0,1]内的随机数p; 输出:接下来执行的state. ① 置随机权值Wrandom为二叉树根结点的Wsum值乘以p; ② 令当前结点为二叉树的根结点; ③ 如果当前结点存在左子结点,转步骤④;否则,转步骤⑦; ④ 如果Wrandom小于当前结点的左子结点的Wsum值,转步骤⑤;否则,转步骤⑥; ⑤ 令当前结点为它的左子结点,返回步骤③; ⑥ 置Wrandom为其原值减去当前结点的左子结点的Wsum值; ⑦ 如果Wrandom小于当前结点的W值,则转步骤⑩;否则,转步骤⑧; ⑧ 置Wrandom为其原值减去当前结点的W值. ⑨ 令当前结点为它的右子结点,返回步骤③. ⑩ 输出当前结点对应的state. 3实验与分析 我们基于符号执行工具KLEE实现了SCPS策略.KLEE是基于LLVM平台的C程序符号执行工具,使用STP作为约束求解器.基于实现的搜索策略和KLEE已有搜索策略,我们开展了一系列的实验,实验想回答3个问题:1)和RPS+COS策略组合相比,SCPS+COS能否提高语句覆盖率;2)和RPS+COS策略组合相比,SCPS+COS能否探索更多路径;3)和RPS+COS策略组合相比,SCPS+COS是否具有更强的缺陷查找能力. 在实验对象上,我们随机选择了GSL(version 1.16)中的12个模块.GSL是一个应用广泛的数值计算C和C++程序库,提供如随机数产生器、特殊函数和最小二乘拟合等功能.经过长期的维护和深度测试,GSL目前已相当成熟.另外,由于目前KLEE无法直接对浮点程序进行符号执行[11],我们引入SoftFloat把12个GSL模块中的浮点运算手工替换成了SoftFloat中提供的操作.SoftFloat是一个高质量的符合IECIEEE标准的整数实现浮点库,支持4种最常见的浮点精度的运算:单精度(32 b)、双精度(64 b)、扩展双精度(80 b)以及4倍精度(128 b)[12].使用SoftFloat中的函数替换GSL程序中的基本运算后我们把这12个模块改编成了12个独立程序,这12个程序及其规模如表2所示,ELOC表示经优化后可在KLEE上执行的测试集程序的可执行代码行数,所有程序的规模在2 700~2 900行之间. 在实验中我们比较了SCPS+COS(我们的方法)和RPS+COS(KLEE已有的效果较好策略)2种策略组合在语句覆盖、探索路径数量以及缺陷查找上的能力.所有实验都是在处理器为Intel®Xeon®X5675 CPU(24 cores,3.07 GHz)、内存为94 GB的服务器上进行的,操作系统是64位的Ubuntu 12.04.1 LTS.使用KLEE对每个程序进行分析时主要设置了以下3个参数∶--max-time=1 800(最大执行时间为1 800 s,即30 min),--max-solver-time=50(最大求解时间为50 s),--search(设置搜索策略).由于对每个搜索策略组合来说都有部分程序无法在到达指定时间时及时终止,且它们超时时长大小不一,为公平起见,我们忽略超时后探索的路径,仅仅比较在指定最大执行时间30 min内生成的路径[13]. Table 2 Executable Line of Code (ELOC) of Test Benchmarks 3.1语句覆盖 语句覆盖就是度量被分析代码中每个可执行语句是否被执行到了.虽然语句覆盖常常被指责为“最弱的覆盖”,但它仍然是最常用也是最常见的一种代码覆盖准则,实验中我们使用gcov统计语句覆盖率信息.统计语句覆盖率时我们只考虑程序自身的可执行代码行数,而不考虑各程序调用的库中的代码.使用不同策略组合分析每个程序时的语句覆盖率如表3所示: Table 3The Statement Coverage of Test Benchmarks Using Different Strategies 表3 使用不同策略组合时的语句覆盖率 % 由于被分析程序中包含大量SoftFloat中的代码,且有的路径约束条件中包含大量复杂运算,在指定最大求解时间内无法对这些约束进行求解,导致语句覆盖率较低.使用SCPS+COS搜索策略时的语句覆盖率均值为12.44%,使用RPS+COS时的语句覆盖率均值为12.62%.虽然SCPS+COS策略组合无法提高语句覆盖率,但我们可以认为SCPS+COS和RPS+COS的语句覆盖能力相当. 3.2路径数 我们统计了使用不同策略组合分析每个程序所探索的路径数(记为N).实验中发现不同被分析的程序所产生的路径数相差特别大,为公平起见,采用路径数提高率(记为I)来统计实验结果,提高率的计算方法为 (4) 图5显示了对12个被分析程序采用SCPS+COS策略组合进行分析时在所探索的路径数量上相对于RPS+COS的提高率,由低到高排列.数据显示,对11个被分析程序进行分析时采用SCPS+COS策略组合在探索的路径数量上要优于RPS+COS,在1个程序上SCPS+COS要比RPS+COS稍差,这是因为该程序的执行树形态比较细长,采用2种策略组合最终所探索的路径基本相同,而SCPS在状态选择时的开销要比RPS稍大.平均而言,采用SCPS+COS策略组合所产生的路径要比采用RPS+COS高出24.34%. Fig. 5 The improved rate of explored paths by SCPS+COS compared with RPS+COS.图5 SCPS+COS相对RPS+COS探索路径提高率 同时,我们统计了探索路径数量随时间的变化情况(对每个被分析程序均以采用RPS+COS策略组合在30 min内所覆盖的路径的总量为100%),图6显示了探索路径数量相对均值随时间变化情况. Fig. 6 The time-dependent change of the relative mean number of explored paths using different strategy combinations.图6 不同策略组合探索的路径数相对均值随时间的变化 可以看出在程序执行初期,使用RPS+COS策略组合所探索的路径数要比SCPS+COS策略多,这是因为刚开始时PC都比较简单,求解开销相差不大,且求解开销和PC复杂度的历史信息较少,求解开销预测准确性不高.随着PC复杂度增加及历史信息积累,求解开销分化越来越大,SCPS的优势逐渐体现,能够在相同时间内探索更多路径.因此,当执行时间够长时,和RPS+COS策略组合相比,SCPS+COS能够探索更多路径. 3.3缺陷查找 进一步,我们希望比较RPS+COS(简称R+C)和SCPS+COS(简称S+C)这2种搜索策略组合在缺陷查找方面的能力.我们使用程序变异工具Milu[14]对被分析的12个程序进行变异,变异后生成的程序叫变异体(mutant). 我们使用Milu共产生了3 639个变异体,然后用KLEE来分析变异后的程序,希望能够发现变异点.在实验中我们使用KLEE对每个变异体进行2次符号执行,分别使用上述2种策略组合,执行时设置最大执行时间为600 s、单次最大求解时间为30 s.表4给出了实验结果. Table 4 The Experimental Results of Bug Finding in Mutants Notes: R+C is short of RPS+COS, and S+C is short of SCPS+COS. 实验共查找出361个缺陷,RPS+COS策略组合能找出其中的346个,SCPS+COS能找出其中的356个,2种策略组合都能查找出的缺陷有341个.对比这2种策略组合查找这341个相同bug的时间开销发现SCPS+COS策略组合查找出其中的215个耗时更短,41个持平,只有81个耗时更长.平均而言,查找相同缺陷时,SCPS+COS策略组合要比RPS+COS减少44.43%,计算方法如式(5)所示,其中STR+C和STS+C是分别使用RPS+COS策略和SCPS+COS策略查找所有相同缺陷时的总时间开销. davg=(STR+C-STS+C)STR+C×100.00%. (5) 从上述实验结果可以看出,对于实验中变异后的程序,SCPS+COS策略组合在相同时间内能够找出更多的缺陷,并且找出相同缺陷需要的时间更短. 3.4有效性 实验中我们从GSL中随机选取了12个模块作为被分析程序,具有一定的代表性.由于GSL本身很成熟,存在的缺陷较少,我们只在变异程序及而非实际程序中找到了更多缺陷.从实验数据可以看出采用SCPS+COS策略组合时查找相同缺陷时间开销的平均减少率(44.43%)要比其探索的路径数量相对提高率(24.34%)高,主要原因如下:1)开销的平均减小率统计的是查找341个相同bug的平均耗时减少水平,探索的路径数量相对提高率在统计时因为不同程序的被探索路径数量相差很大,为公平起见统计的是这12个程序的平均提高率,不是所有路径总和的提高率(37.82%);2)SCPS策略优先探索求解开销较小的路径,随着后续简单路径越来越少,将不得不探索一些更为复杂的路径,和RPS相比的优势也将减弱. 4相关工作 为缓解符号执行的路径爆炸问题,提高语句覆盖率及缺陷查找能力,研究者们提出了很多搜索策略、查询优化方法及并行优化技术. 在搜索策略方面,Cadar等人[15]开发的工具EXE中采用了一种最佳优先搜索策略(best-first search),根据相应的目标采用启发式搜索算法选择所有候选执行状态中最符合该目标的一个执行状态.Burnim等人[16]也使用启发式信息引导动态符号执行的搜索过程,他们构建了一个被分析程序的加权控制流图,通过比较控制流图中各未覆盖过的语句和当前位置的距离优先探索最近的程序块.为了查找特定的语句中是否存在缺陷,Ma等人[7]提出了面向程序中某个位置的符号执行搜索策略,基于在过程间控制流图上到目标语句的最短路径进行探索.面向目标的符号执行方法[7]在指定的搜索目标的引导下,交替使用后向和前向的搜索方式,能够快速地查找出覆盖目标程序点的路径.相比而言,本文提出的搜索策略是从符号执行中约束求解的角度来提高符号执行的搜索能力,与上述一些策略是互补的关系,可以组合使用. 在查询优化方面,KLEE实现了以下优化方法[4]:通过重写简化表达式、进行独立性检查以消除无关约束以及通过反例缓存获取求解结果,取得了不错的效果.文献[17]中提出了猜测符号执行方法,将现代处理器流水结构中的猜测思想引入到符号执行中,仅当路径上未判定分支语句个数达到一定数量或到达叶结点时才对路径的可行性进行判断,从而可以减少约束求解的次数.文献[18]中设计了一种能够自动选择时机和方式进行状态合并的动态优化方法,通过状态合并减少了待遍历的路径数.Visser等人[19]提出了Green框架,Green独立于符号执行工具,它能够将之前的求解结果存储在内存数据库中.这种存储方式使得同一程序的不同分析过程、不同求解器调用以及不同程序的分析过程、不同机器之间能够共享缓存信息.相比而言,本文的工作是通过约束求解的开销来引导符号执行的搜索过程,上述一些工作可能会与我们提的搜索策略有冲突,比如文献[18]中的方法会增加路径条件的复杂度.因此,我们的策略如何与已有查询优化方法相结合是下一步需要研究的内容. 并行优化技术[20-22]是符号执行技术研究的一个重要方向.并行优化技术主要是采用不同的算法将程序的路径空间进行划分,同时使用不同的计算单元对划分后的路径空间不同部分进行探索;并行优化技术还需要考虑不同计算单元之间的信息交互及负载均衡.目前,很多并行优化算法在缓解符号执行的路径爆炸问题上取得了很好的效果.但是,理论上,并行优化技术的最大收益与计算单元的数量呈线性关系,而路径数却与分支数呈指数关系,并行优化技术并不能从根本上解决路径爆炸问题. 5总结 提出并实现了一种基于求解开销预测的符号执行搜索策略.实验表明,相比现有搜索策略,本文提出的策略可以在保证相当语句覆盖率的前提下,探索更多的程序路径(24.34%的提升);在缺陷查找方面,针对被分析程序的3 639个变异体进行分析,使用本文提出的策略多可多发现10个软件缺陷,并且对于相同的程序缺陷,本文中策略发现这些缺陷需要的耗时平均减少了44.43%.后续研究将主要从3个方面开展: 1) 改进求解开销预测算法; 2) 从基本路径覆盖率、平均代码覆盖率以及平均错误检测率等方面上进一步比较SCPS+COS和其他搜索策略; 3) 对更多实际程序进行分析,进一步比较SCPS+COS和其他搜索策略在缺陷查找方面的能力. 参考文献 [1]Zhang Jian. Sharp static analysis of programs [J]. Chinese Journal of Computers, 2008, 31(9): 1549-1553 (in Chinese)(张健. 精确的程序静态分析[J]. 计算机学报, 2008, 31(9): 1549-1553) [2]King J C. Symbolic execution and program testing [J]. Communications of the ACM, 1976, 19(7): 385-394 [3]Cadar C, Godefroid P, Khurshid S, et al. Symbolic execution for software testing in practice: preliminary assessment [C]Proc of the 33rd Int Conf on Software Engineering. New York: ACM, 2011: 1066-1071 [4]Cadar C, Dunbar D, Engler D R. KLEE: Unassisted and automatic generation of high-coverage tests for complex systems programs [C]Proc of the 8th USENIX Symp on Operating Systems Design and Implementation. Berkeley, CA: USENIX Association, 2008: 209-224 [5]Jaffar J, Navas J A, Santosa A E. Unbounded symbolic execution for program verification [C]Proc of the 2nd Int Conf on Runtime verification. Berlin: Springer, 2012: 396-411 [6]Bugrara S, Engler D R. Redundant state detection for dynamic symbolic execution [C]Proc of the 2013 USENIX Annual Technical Conf. Berkeley, CA: USENIX Association, 2013: 199-211 [7]Ma K, Phang K, Foster J, et al. Directed symbolic execution [G]Static Analysis. Berlin: Springer, 2011: 95-111 [8]Person S, Yang G, Rungta N, et al. Directed incremental symbolic execution [J]. ACM SIGPLAN Notices, 2011, 46(6): 504-515 [9]Ganesh V, Dill D L. A decision procedure for bit-vectors and arrays [C]Proc of the 19th Int Conf on Computer aided verification. Berlin: Springer, 2007: 519-531 [10]Free Software Foundation (FSF). GSL: GNU scientific library [EBOL]. [2014-07-31]. http:www.gnu.orgsgsl [11]Romano A. Practical floating-point tests with integer code [C]Proc of the 15th Int Conf on Verification, Model Checking, and Abstract Interpretation. Berlin: Springer, 2014: 337-356 [12]Hauser J. Berkeley SoftFloat [EBOL]. [2014-07-31]. http:www.jhauser.usarithmeticSoftFloat.html [13]Li Y, Su Z, Wang L, et al. Steering symbolic execution to less traveled paths [J]. ACM SIGPLAN Notices, 2013, 48(10): 19-32 [14]Jia Y, Harman M. MILU: A customizable, runtime-optimized higher order mutation testing tool for the full C language [C]Proc of the 3rd Testing: Academic and Industrial Conf—Practice and Research Techniques. Piscataway, NJ: IEEE, 2008: 94-98 [15]Cadar C, Ganesh V, Pawlowski P M, et al. EXE: Automatically generating inputs of death [C]Proc of the 13th ACM Conf on Computer and Communications Security. New York: ACM, 2006: 332-335 [16]Burnim J, Sen K. Heuristics for scalable dynamic test generation [C]Proc of the 23rd Int Conf on Automated Software Engineering. Los Alamitos, CA: IEEE Computer Society, 2008: 443-446 [17]Zhang Y, Chen Z, Wang J. Speculative symbolic execution [C]Proc of the 23rd Int Symp on Software Reliability Engineering (ISSRE). Piscataway, NJ: IEEE, 2012: 101-110 [18]Kuznetsov V, Kinder J, Bucur S, et al. Efficient state merging in symbolic execution [J]. ACM SIGPLAN Notices, 2012, 47(6): 193-204 [19]Visser W, Geldenhuys J, Dwyer M B. Green: Reducing, reusing and recycling constraints in program analysis [C]Proc of the 20th ACM SIGSOFT Int Symp on the Foundations of Software Engineering. New York: ACM, 2012: 58-68 [20]King A. Distributed parallel symbolic execution [D]. Manhattan, Kansas: Kansas State University, 2009 [21]Ciortea L, Zamfir C, Bucur S, et al. Cloud9: A software testing service [J]. ACM SIGOPS Operating Systems Review, 2010, 43(4): 5-10 [22]Staats M, Pǎsǎreanu C. Parallel symbolic execution for structural test generation [C]Proc of the 19th Int Symp on Software Testing and Analysis. New York: ACM, 2010: 183-194 Liu Jingde, born in 1990. Master. Student member of China Computer Federation. His research interests include high confidence software and system, symbolic execution. Chen Zhenbang, born in 1981. PhD and assistant professor. His current research interests include program analysis and verification, component-oriented software engineering. Wang Ji, born in 1969. PhD. Professor and PhD supervisor. Senior member of China Computer Federation. His main research interests include high confidence software and system, software engineering and distributed computing. Solving Cost Prediction Based Search in Symbolic Execution Liu Jingde1,3, Chen Zhenbang1, and Wang Ji1,2 1(CollegeofComputer,NationalUniversityofDefenseTechnology,Changsha410073)2(ScienceandTechnologyonParallelandDistributedProcessingLaboratory(CollegeofComputer,NationalUniversityofDefenseTechnology),Changsha410073)3(95835PLATroops,Bayingolin,Xinjiang841700) AbstractIn symbolic execution, constraint solving needs a large proportion of execution time. The solving time of a constraint differs a lot with respect to the complexity, which happens a lot when analyzing the programs with complex numerical calculations. Solving more constraints within a specified time contributes to covering more statements and exploring more paths. Considering this feature, we propose a solving cost prediction based search strategy for symbolic execution. Based on the experimental data of constraint solving, we conclude an empirical formula to evaluate the complexity of constraints, and predict the solving cost of a constraint combined with historical solving cost data. The formula is used in our strategy to explore the paths with a lower solving cost with a higher priority. We have implemented our strategy in KLEE, a state-of-art symbolic executor for C, and carried out the experiments on the randomly selected 12 modules in GNU Scientific Library (GSL). The experimental results indicate that: in a same period, compared with the existing strategy, our strategy can explore averagely 24.34% more paths, without sacrificing the statement coverage; and our strategy can find more bugs. In addition, the time of using our strategy for finding same bugs decreases 44.43% in average. Key wordssymbolic execution; constraint solving; weighted random search; bug finding; statement covering 收稿日期:2014-12-08;修回日期:2015-03-26 基金项目:国家“九七三”重点基础研究计划基金项目(2014CB340703);国家自然科学基金项目(61120106006,61472440,61272140) 中图法分类号TP311 This work was supported by the National Basic Research Program of China (973 Program) (2014CB340703) and the National Natural Science Foundation of China (61120106006,61472440,61272140).