二元一般指数分布的识别性及其参数估计

李卫华，　李国安，　王　伟，　李茂华

(宁波大学理学院，浙江宁波315211)



二元一般指数分布的识别性及其参数估计

李卫华，李国安，王伟，李茂华

(宁波大学理学院，浙江宁波315211)

[摘要]讨论了一般二元指数分布的识别性问题及参数估计问题.本文证明了两个结论：其一、当只有最大值随机变量的分布已知时，仅一个参数可识别；其二、当可识别最大值的分布已知时，所有参数皆可识别.进一步根据上述结论得到了所有参数的最大似然估计.

[关键词]一般二元指数分布； 识别性； 最大似然估计

1引言

Gupta，Kundu于1999年在文献[1]中提出了一个一般指数分布，在2009年，Kundu，Gupta在文献[2]中导出了一个一般二元指数分布，本文讨论二元一般指数分布的识别性问题及其参数估计.所谓参数的识别性是指总体分布的参数是否能被随机变量的某些函数的分布所唯一确定，若能，则称参数是可识别的.显然，参数的识别性是其可估计的先决条件.文[3-13]讨论了二元正态分布、三元正态分布、及多元正态分布的参数的识别性，在本文中，讨论二元一般指数分布的参数的识别性问题.本文具体分两种情况讨论其参数的识别性问题.第一种情况为仅知道两个随机变量最大值的分布，这时只有部分参数能识别.为了能够识别所有六个变量，则需要添加其他条件，本文通过添加两随机变量的比较识别变量来实现，具体见后文的分析.

2二元一般指数分布的识别性

文[2]给出了如下的二元一般指数分布的定义，具体见定义1.

定义1称二维随机变量(X1,X2)服从二元一般指数分布，若其有如下的分布函数

F(x1,x2)=(1-e-λx1)α1(1-e-λx2)α2(1-e-λmin(x1,x2))α3，x1>0,x2>0，

记作

(X1,X2)～BVGE(α1,α2,α3,λ)，

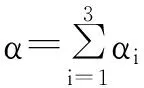
下面讨论两随机变量的最大值的分布已知时，二元一般指数分布的参数的识别性问题.为讨论的方便，引入两个随机变量

U=max(X1,X2),

(1)

(2)

并记U的密度函数和分布函数分别记为g(z)和G(z)，二维随机变量(U,I)的密度函数为h(u,i),其中z∈+，i∈{1,2,3}.二元一般指数分布的参数的识别性问题，具体定义见定义2.

定义2设二元随机变量(X1,X2), (X′1,X′2)服从同类型的分布，且

(X1,X2)～ F (X1,X2, θ)，(X′,Y′)～ F (X′,Y′,θ′)，

这里θ，θ′同为参数或参数向量，并如(1), (2)两式引入随机变量(U,I) 和(U′,I′).若G(z)=G′(z)蕴含θ=θ′，则参数在此情形下是可识别的，否则参数在此情形下是不可识别的；类似地，若h(z,i)=h′(z,i)蕴含θ=θ′，则称参数在此情形下是可识别的，否则参数在此情形下是不可识别的.

引理1若(X1,X2)～BVGE(α1,α2,α3,λ)，则U的分布密度为

g(u)=αλe-λu(1-e-λu)α-1,u>0.

证由P(U≤u)=P(max(X1,X2)≤u)=P(X1≤u,X2≤u)=F(u,u)

=(1-e-λu)α1(1-e-λu)α2(1-e-λmin(u,u))α3=(1-e-λu)α，

得

g(u)=αλe-λu(1-e-λu)α-1,u>0.

引理2若(X1,X2)～BVGE(α1,α2,α3,λ)，则(U,I)的分布密度为

证二元一般指数分布为混合分布，现对其三部分x1>x2, x1

当x1>x2时，分布函数

F1(x1,x2)=(1-e-λx1)α1(1-e-λx2)α2(1-e-λx2))α3=(1-e-λx1)α1(1-e-λx2)α2+α3，

所以

同理，当x1

f2(x1,x2)=α2(α1+α3)λ2e-λ(x1+x2)(1-e-λx2)α2-1(1-e-λx1)α1+α3-1.

P(U≤u,I=1)=P(max(X1,X2)≤u,I=1)=P(X1≤u,X1>X2)

所以

h(u,1)=α1λe-λu(1-e-λu)α-1，

同理

h(u,2)=α2λe-λu(1-e-λu)α-1.

当x1=x2时

F1(x1,x1)=(1-e-λx1)α1+α2+α3，

所以

h(u,3)=αλe-λu(1-e-λu)α-1.

定理1设

(X1,X2)～BVGE(α1,α2,α3,λ)，(X′1,X′2)～BVGE(α′1,α′2,α′3,λ′)，

若已知U与U′同分布，则只有参数λ可识别，其余参数皆不可识别.

证由g(u)=g′(u)，得

αλe-λu(1-e-λu)α-1=α′λ′e-λ′u(1-e-λ′u)α′-1u>0,

首先得λ=λ′，α=α′.因此，参数λ可识别； α1,α2,α3均不可识别，但三者的和可识别.

定理2设

(X1,X2)～BVGE(α1,α2,α3,λ)，(X′1,X′2)～BVGE(α′1,α′2,α′3,λ′)，

若已知(U,I)与(U′,I′)同分布，则所有参数皆可识别.

证由h(u,i)=h'(u,i)，得

αiλe-λu(1-e-λu)α-1=α′iλ′e-λ′u(1-e-λ′u)α′-1,i=1,2,u>0,

得λ=λ′,α=α′,α1=α′1,α2=α′2，进而得α3=α′3.因此，所有参数可识别.

3二元一般指数分布的参数估计

文献[2]研究了二元一般指数分布的参数估计，这里，我们从定理1和定理2出发，直接分别获得了参数λ，以及所有参数的最大似然估计.

定理3设(X1,X2)是总体，(X11,X21),…,(X1n,X2n)是来自总体(X1,X2)的容量为n的样本，记

U=max(X1,X2)，Ui=max(X1i,X2i)，i=1,…,n，

若U具有以下的分布密度

g(u)=αλe-λu(1-e-λu)α-1,u>0，

U1,…,Un是来自总体U的容量为n的样本，u1,…,un为样本值，则参数λ的最大似然估计为下列方程的解

(3)

证

其对数似然函数的驻点方程为

求解，即得结论.

定理4设(X1,X2)是总体，(X11,X21),…(X1n,X2n)是来自总体(X1,X2)的容量为n的样本，按前文(1)，(2)两式引入U,I，同时记Ui=max(X1i,X2i)，Ii=φ(X1i,X2i).现假定(U,I)具有如引理2所述的分布密度，(U1,I1),…,(Un,In)是来自总体(U,I)的容量为n的样本.U的样本值记为u1,…,un，并记

α1，α2，α3的最大似然估计为

证似然函数为

对数似然函数的驻点方程为

得参数λ满足方程

结论仅是U的分布已知时，只有参数λ可识别，即只有参数λ可估计，当(U,I)的分布已知时，所有参数皆可识别，即所有参数皆可估计.

[参考文献]

[1]Gupta R D，Kundu D. Generalized exponential distributions[J]. Australian and New Zealand Journal of Statistics, 1999, 41: 173-188.

[2]Kundu D，Gupta R D. Bivariate generalized exponential distributions [J]. Journal of Multivariate Analysis, 2009, 100: 581-593.

[3]Anderson T W, Ghurye S D. Identification of parameters by the distribution of a maximum random variable [J]. Journal of the Royal Statistical Society: Series B， 1977, 39(3): 337-342.

[4]Basu A P, Ghosh J K. Identifiability of the multinormal and other distributions under competing risks model [J]. Journal of Multivariate Analysis， 1978, 8(3): 413-429.

[5]Gilliland D C, Hannan J. Identification of the Ordered Bivariate Normal Distribution by Minimum Variate [J]. Journal of the American Statistical Association， 1980, 75: 651-654.

[6]Mukherjea A, Stephens R. The problem of identification of parameters by the distribution of the maximum random: Solution for the trivariate normal case[J].Journal of Multivariate Analysis, 1990, 34(1): 95-115.

[7]Mukherjea A, Stephens R. Identification of parameters by the distribution of the maximum random variable: The general multivariate normal case[J]. Probability Theory and Related Fields，1990, 34(1): 289-296.

[8]Gong J, Mukherjea A. Solution of a problem on the identification of parameters by the distribution of the maximum random variable: a multivariate normal case[J]. Journal of Theoretical Probability, 1991, 4(4): 783-790.

[9]Mukherjea A, Stephens R. Identification of the parameters of a trivariate normal vector by the distribution of the minimum [J]. Journal of Statistical Planning and Inference, 1999, 78(1): 23-37.

[10]Dai M, Mukherjea A. Identification of the parameters of a multivariate normal vector by the distribution of the maximum [J]. Journal of Theoretical Probability, 2001, 14: 267-298.

[11]Davis J, Mukherjea A. Identification of parameters by the distribution of the minimum: The tri-variate normal case with negative correlations [J]. Journal of Multivariate Analysis, 2007, 98(6): 1141-1159.

[12]Bi L, Mukherjea A. Identification of parameters and the distribution of the minimum of the tri-variate normal [J]. Statistics & Probability Letters, 2010, 80(23): 1819-1826.

[13]Mukherjea A, Elnaggar M. Solution of the problem of the identified minimum for the tri-variate normal [J]. Proceedings - Mathematical Sciences, 2012, 4(122): 645-660.

Identifiability of the Bivariate Generalized Exponential Distributions

LIWei-hua，LIGuo-an,WANGWei,LIMao-hua

(Department of Mathematics, Ningbo University, Ningbo Zhejiang 315211, China)

Abstract:If two random variable has a bivariate generalized exponential distribution，when the distribution of the maximum is known，then only one of parameters is identified，when the distribution of the identified minimum is known，then all of parameters are identified；hence，the maximum likelihood estimator of all of parameters are derived.

Key words:bivariate generalized exponential distribution； identifiability； maximum likelihood estimator

[收稿日期]2014-10-13；[修改日期] 2016-03-08

[基金项目]浙江省自然科学基金(LQ12A01006)；浙江省自然科学基金(LY15A010005)

[作者简介]李卫华(1979-),男，硕士，实验师，从事数值计算、应用统计等研究.Email: liweihua@nbu.edu.cn

[中图分类号]O29；TE312

[文献标识码]C

[文章编号]1672-1454(2016)02-0081-05