具有非负Ricci曲率流形的一些拓扑性质
2016-06-16张易
张 易
(同济大学数学系,上海200092)
具有非负Ricci曲率流形的一些拓扑性质
张易
(同济大学数学系,上海200092)
[摘要]自从Milnor的基础性论文[5]发表以来,研究非负Ricci曲率的完备非紧流形的拓扑性质就成为一个热门的研究领域,其中代表性的问题为Milnor猜想.Anderson应用体积估计和万有覆盖空间的方法,对此类流形的拓扑性质进行了一定的研究[1-2].本文扩展Anderson的方法,进一步的给出更加一般条件下此类流形的拓扑性质,并对高阶同伦群的研究给出了一些方法.
[关键词]非负Ricci曲率; 拓扑性质; 体积估计
在[3]中,Cheeger证明了一个关于满足KM≥-λ,volM≥v和diamM≤D条件的紧致Rieman流形M的最短非平凡闭测地线的长度的估计l(γ).在[1]中,若[γ]在π1(M)足够的非平凡,则在条件RicM≥-λ,volM≥v和diamM≤D下,Anderson给出了关于γ的长度的估计.在本文中,我们应用这几篇文章[1-3]的技巧,来给出有关非负Ricci曲率流形的一些拓扑性质.
首先,陈述记号以及M满足的条件.
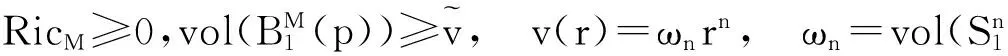
(1)

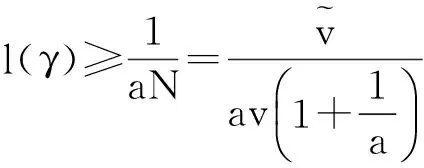
(2)

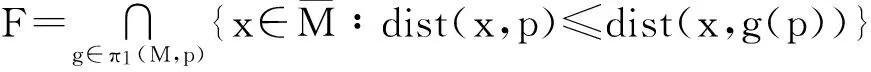
则有
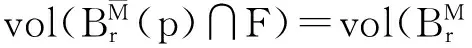
(3)
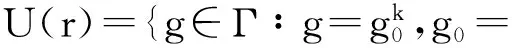
dist(g(p),p)≤r·l(γ)
对任何g∈U(r)成立.现在选取最小的r=r0使得|U(r0)|≥N,由三角不等式得
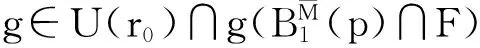
(4)
对(4)式两边同时取体积,计算可得

(5)


(6)

(7)

ord(g)=min{s:gs=e,s∈N+}.

(8)

定理2设M为一个完备非紧RicM≥0的流形,且存在一个α>0和一个ε>0,使得对任何的R,都有
vol(BR(p))≥αRn-1+ε,
则对任意的g∈π1(M,p),有ord(g)<∞.


则dist(gp,p)≤r·maxl(γi)对任何g∈U(r)成立.因此类似上文的论证,可得
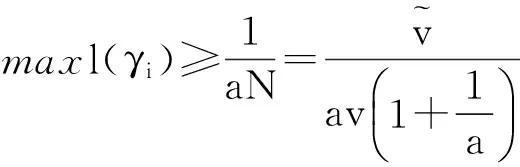
(9)
倘若|Γ|≥N.
注2应用注1和定理1的论证,可得下述定理3和推论1,[2]和[4]采用了不同的方法得到此结果.


类似的,应用注1和定理2的论证,可得
定理4设M为一个完备非紧RicM≥0的流形,且存在一个α>0和一个ε>0,使得对任何的R,都有vol(BR(p))≥αRn-1+ε, 则对任何有限生成的Γ≤π1(M,p),有|Γ|<∞.
注3证明的核心思想是,当对流形放缩的时候,M的拓扑性质是不变的,但M的一些几何性质在变化.因此当一些拓扑条件可以导出一些几何量的控制时,就可以通过这些控制导出一些矛盾,由此得到一些拓扑信息.例如,在一些拓扑条件下,对某些非平凡的k维胞腔Sk,有估计
vol(Sk)≥C·vol(B1(p)),
(10)
则用放缩后,可得
vol(Sk)≥C·Rkvol(BR(p)).
(11)
倘若M的塌缩速度不是特别的快,使得当R→∞时,(11)式的右侧也能趋于∞,则我们可以得到一个矛盾,由此给出流形的拓扑信息.
最后,给出定理3的一些进一步的结果.记

假设|U(r)|≥c0rk.采用这些记号,有

(12)
记l=maxl(γi),则有
c0rk·vol(B1(p))≤ωn(r·l+1)n.
(13)
对于放缩后的流形Mi,由上面得到的不等式,得到

(14)

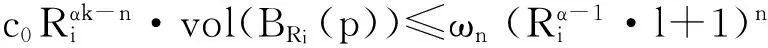
(15)
令Ri→∞,则(15)式的右边趋于ωn.然而若

就得到了一个矛盾.因此得到
定理5设M为一个完备非紧RicM≥0的流形,且存在0<α<1,ε>0和v0>0,使得
vol(BR(p))≥v0Rn-αk+ε,
则不存在有限生成的Γ≤π1(M,p),满足其增长阶大于k.
固定k,对于任何有限生成的Γ≤π1(M,p),记

其中c(Γ)可以是∞.有上述讨论,给定任何ε>0,对于某些充分大的R,有
(c(Γ)-ε)Rαk-n·vol(BR(p))≤ωn(Rα-1·l+1)n.
(16)
假设

定理6设M为一个完备非紧RicM≥0的流形,且对于某个0<α<1,有

推论2设M为一个完备非紧RicM≥0的流形,且对于某个s>0,有
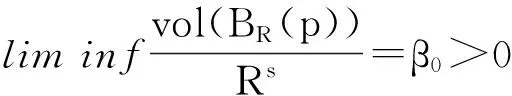
注4若我们知道,对任何有限生成的Γ≤π1(M,p),存在一个一致的R,使得对任何r≥R,有|U(r)|≤2c0rk,那么对于这样的假设情形,易知π1(M,p)是有限生成的,且其增长阶≤k.
[参考文献]
[1]Anderson M T. Short geodesics and gravitational instantons[J]. J. Diff. Geom.,1990(31): 265-275.
[2]Anderson M T. On the topology of complete manifolds of non-negative Ricci curvature[J]. Topology, 1990,29(1): 51-55.
[3]Cheeger J. Finiteness theorems for Riemannian manifolds[J]. Amer. J. Math., 1970(92): 61-74.
[4]Li P. Large time behavior of the heat equation on complete manifolds with non-negative Ricci curvature[J]. Ann. Math. Second Series, 1986,124(1): 1-21.
[5]Milnor J. A note on curvature and fundamental group[J]. J. Diff. Geom., 1968(2): 1-7.
Some Topological Information of Manifolds with Non-negative Ricci Curvature
ZHANGYi
(Institute of Mathematics, Tongji University, Shanghai 200092, China)
Abstract:From the fundamental paper of Milnor[5], the research of complete, non-compact and non-negative Ricci curvature is very hot. The representative problem of this field is Milnor’s conjecture. By using the methods of volume estimate and universal covering space, Anderson gives some results of topology of these manifolds. In this paper[1-2], we generalize the methods of Anderson and give some topological results of these manifolds under some generalized conditions and some methods for researching the higher order homotopy groups.
Key words:non-negative Ricci; topological properties; volume estimates
作者简介:开晓山,合肥工业大学数学学院副教授,博士,硕士生导师,长期从事编码理论研究工作,主持国家自然科学基金面上项目、安徽省自然科学基金项目、东南大学移动通信国家重点实验室开放研究基金项目、中央高校基本研究基金项目等课题研究. 在IEEE Transactions on Information Theory、Designs Codes & Crytography、Finite Fields and Their Applications、Discrete Mathematics等国际期刊上发表SCI论文20余篇. 2014年,在国际期刊IEEE Transactions on Information Theory上发表的论文:Constacyclic codes and some new MDS codes入选ESI高被引用论文. 张易(1989-),男,博士研究生,从事黎曼几何与度量几何的研究. Email:08zhangyi@tongji.edu.cn
[收稿日期]2016-02-01;[修改日期] 2016-03-25
[基金项目]国家自然科学基金(11471247)
[中图分类号]O186.12
[文献标识码]A
[文章编号]1672-1454(2016)02-0008-04
