一种基于HHT的短期电价组合预测方法

廖晓辉，周　冰，杨冬强，武　杰

一种基于HHT的短期电价组合预测方法

廖晓辉1，周冰1，杨冬强1，武杰2

(1.郑州大学 电气工程学院，河南 郑州 450001； 2.郑州市供电公司， 河南 郑州 450051)

摘要：短期电价预测保障了电力市场中各参与方的最大效益，针对非平稳非线性的电价序列，提出了一种基于Hilbert-Huang变换的组合预测模型.首先将电价序列进行经验模态分解，得到若干固有模态函数分量及余项，其次根据各分量变化规律分别进行预测，最后将各分量的预测结果相加即为电价预测值.并以美国 PJM (Pennsylvania-New Jersey-Maryland)电力市场的实际数据进行仿真，将各算法的预测结果进行比较，得出此方法预测精度均高于单一预测模型，其最大绝对误差为1.53S|/MWh，平均绝对误差为1.61%，由此表明，该模型具有较高的预测精度.

关键词：电力市场；电价预测；HHT；组合预测

0引言

电能作为一种商品，在电力市场中的流向和配给是以电价作为向导，故准确的短期电价预测有着重要的意义，有助于市场参与者制订合理的竞争策略，实现风险最小，收益最大的目标，是参与者共同关注的一项重要工作，是电力市场短期电价交易中亟待解决的问题之一[1].

短期电价预测常用的方法主要有时间序列法、人工神经网络、粒子群算法、模糊理论、小波变换等.文献[2]比较了各种电力市场电价模式，发现不同市场中电价有着很大的差异；文献[3-4]利用粒子群优化算法建立短期电价预测模型；文献[5]建立了模糊最小二乘支持向量机模型，预测精度提高且复杂程度基本不变；文献[6-7]本质上都是使用人工神经网络对电价序列进行短期的预测建模；文献[8-9]是利用小波分解对各电价分量分别预测而得到预测日电价.组合预测可将不同预测方法所得到的结果进行优化组合，综合利用各个模型所提供的信息，从而有效地避免了单一模型的不足.

市场电价序列的随机波动性成为电价预测的难点之一.而Hilbert-Huang变换(HHT)基于自身优点对处理这种突变信号有着先天优势，与现有方法中将历史数据整体进行训练预测不同，HHT自适应地将原始数据分解出具有局部时变特征的固有模态函数，相对小波分解又不必预先设定基函数，具有良好的时频聚集性[10].文献[11]将HHT应用于电力系统负荷预测，利用传统的线性组合预测方法，赋予各模型预测结果恒定权值.文献[12-13]将HHT应用于电价预测中，只是对分解所得的固有模态函数采用同一模型分别预测，并且未考虑各函数分量的不同特点.

笔者提出了一种基于HHT的短期电价预测方法，运用经验模态分解将原始电价数据进行平稳化处理，分解出几个具有局部特征的固有模态函数分量和余项，并由各分量的频率区分出高频和低频分量，其中对低频分量选择一种预测模型即可，而高频分量采用组合预测效果更佳，各分量的预测结果之和就是最终预测日电价.采用美国PJM电力市场日前加权平均电价实际数据作为样本[14]，并与各个单一预测模型进行了比较.

1Hilbert-Huang变换原理

Hilbert-Huang变换由Huang等人提出[15]，主要包含经验模态分解(EMD)和Hilbert谱分析两部分.EMD分解是将原信号分解为一系列固有模态函数(IMF)和余项， IMF必须满足两个条件：①所有数据的极值点数与过零点数相等或差一个；②极大值点和极小值点分别形成的上、下包络线的平均值为零.EMD分解时间序列x(t)的过程如下：

1)找出x(t)中的所有极大、小值点，用三次样条曲线分别连接所有极大值和极小值点就形成了原波形的上、下包络线.

2)由式(1)求出上、下包络线之间的平均值，记为m1(t)，E1、E2分别为上、下包络线的值.

(1)

3)求出原始序列与上下包络线之间平均值的差值，即

h1(t)=x(t)-m1(t).

(2)

4)若h1(t)满足IMF的条件，则

c1(t)=h1(t).

(3)

式中：c1(t)为第一个IMF分量.

5)如果h1(t)不满足，将其作为新的输入信号，转至第1)步，计算出h11(t)，重复以上方法，直到h1k(t) 满足IMF 的条件为止，此时：

c1(t)=h1k(t).

(4)

6)将c1(t)从原始序列x(t)中分离出来，则得到：

r1(t)=x(t)-c1(t).

(5)

7)若r1(t)满足终止条件，那么EMD分解结束，如果不满足，那么将r1(t)作为新的输入信号，转至第1)步.重复以上步骤，共得到m个IMF和一个余项rm(t)：

rm(t)=rm-1(t)-cm(t).

(6)

EMD的终止条件有两种，分别为：①预先设定一个终止值，当残余量r小于该预定值时，分解结束；②如果残余量r为一个单调函数，也就是意味着不能再分解出IMF分量时，分解结束.

原始信号x(t)可以表示为m个IMF分量和残余分量之和，即

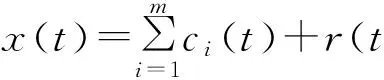
(7)

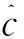
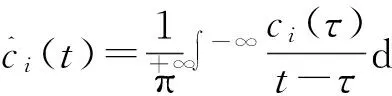
(8)

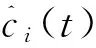
(9)

其相位函数和幅值函数为：

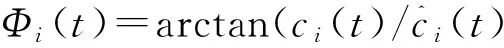
(10)

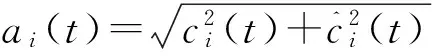
(11)

瞬时频率为

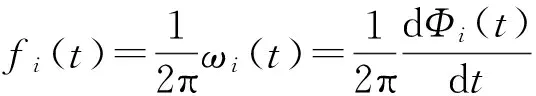
(12)

对各IMF分量进行Hilbert变换(HT)，得出各分量的瞬时频率变化情况，突出了信号的局部特征，对处理突变信号非常适用.

2基于HHT的短期电价预测

2.1预测模型

电价预测方法有很多，各种预测方法均有其不同的特点和适用范围.单一预测模型在一定场合下根据自身优点能够获得较好的预测结果，但都有其局限性，而组合预测模型更全面，其预测精度要高于每个单一模型.下面介绍本文中用到的3种单一预测模型以及组合预测模型.

1)RBF神经网络模型.Powell于1985年提出径向基函数(radial basis funetion,RBF)神经网络[16]，它是根据人的大脑皮层受到刺激时所作出的反应原理构建的，是一种多层前向型的神经网络，具有全局逼近性质，能避免局部最小问题，且有较强的泛化能力.

2)最小二乘支持向量机模型.支持向量机(SVM)[17]是一种基于结构风险最小化的学习训练方法，具有很强的泛化能力.在此基础上最小二乘支持向量机(LS-SVM)将SVM的不等式约束变成了等式约束，降低了SVM的计算复杂度，同时解决了大样本计算速度慢的问题，用于电价预测具有一定的优势.

3)粒子群优化算法模型.粒子群优化(PSO)算法[18]是基于群智能的优化算法，利用群体智能理论来模拟鸟群觅食过程，在个体的合作与竞争中产生群集智能.每个粒子在解空间中运动，并由速度决定他的运动方向和距离，粒子通过对自身的个体最好位置与群体的全局最好位置来动态地调整自己的位置信息，向最优点靠拢.对于PSO中惯性权重的选择至关重要.

4)组合预测模型.传统组合预测将实际值与各模型的预测值之间看成是线性关系，利用数学方法求出各自的权重.笔者采用非线性组合预测，利用BP神经网络的非线性拟合能力，BP网络输入的是各模型的预测值，而实际电价值作为输出来训练网络[19].设各预测模型的第i次预测值分别为P1i、P2i、P3i,电价的第i次实际值记为Pi，它们之间的非线性关系如下：

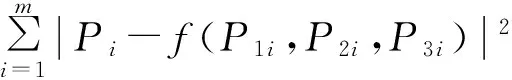
(13)

式中:m为样本个数，本文由3层BP神经网络来逼近上述非线性映射f(·)，使得式(13)取得最小值，因此将各网络预测值输入BP神经网络训练，实际值即为输出的电价预测值.

2.2预测方法

本研究方法步骤如下：

1)对电价数据进行归一化处理，减少噪声对EMD分解的干扰，降低分解层数；

2)对电价序列进行EMD分解，得到若干不同频率的IMF分量和余项；

3)分别对各IMF分量进行Hilbert变换，掌握各分量频谱变化规律，再得出各分量的平均瞬时频率；

4)对有明显周期性的低频IMF分量和余项分别选择一种合适的预测模型；

5)对频率值较高、变化波动较大的高频分量，采用单一的预测方法往往效果不佳，笔者采用组合预测模型；

6)将各个IMF分量预测值相加得到最终预测结果，与实际电价对比，计算误差指标.

2.3评价指标

对预测结果进行评价是考察预测模型精确度的有效手段.预测误差是衡量预测方法效果的主要指标，笔者采用绝对误差、平均绝对误差和平均相对百分误差.设Ri为实际值，Yi为预测值，计算公式如下.

绝对误差：

Ei=Ri-Yi.

(14)

平均绝对误差：

(15)

平均绝对百分误差：

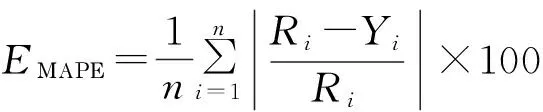
(16)

3仿真算例分析

选取美国PJM电力市场 2014年10月2日至10月30日的实际数据作为样本，来预测10月31日24 h的电价数据.PJM日前市场采用本地边际电价定价方式，按小时出清.PJM市场还公布了一个日前加权平均电价，笔者是以此电价为样本，对原始电价数据经过EMD分解为7个IMF分量和一个余量res，如图1所示.对各分量进行Hilbert变换得到各IMF分量的频谱，如图2所示.

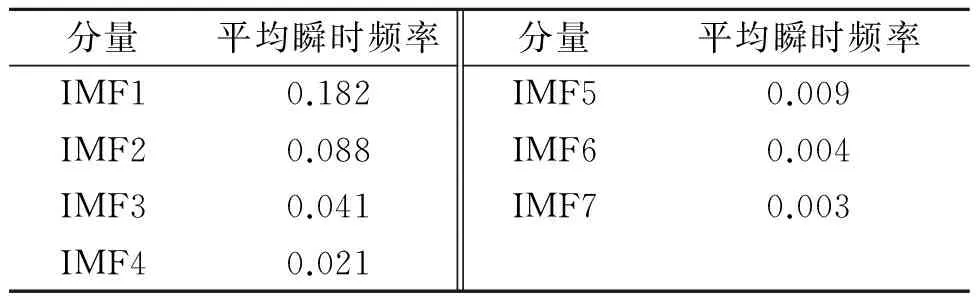
由图2求得各分量的平均瞬时频率如表1所示.从表1可以看出，各IMF分量几乎成1/2的衰减关系.根据各分量的不同特点，分别采用不同的预测模型.IMF1分量，其频率最高，主要为电价的随机成分，波动性很明显，因此对IMF1分量分别采用RBF神经网络、LS-SVM和粒子群算法进行预测，将多次预测的结果作为BP3-8-1 结构神经网络的输入，实际值作为输出来训练网络，设置最大迭代次数为10 000次，学习率为0.05，精度为10-4，训练次数达到8 255次输出结果.IMF2和IMF3分量，其平均瞬时频率较高，波动性较大，采用LS-SVM模型预测；IMF4-7和余量res，其频率较低，周期性明显，采用RBF神经网络模型.

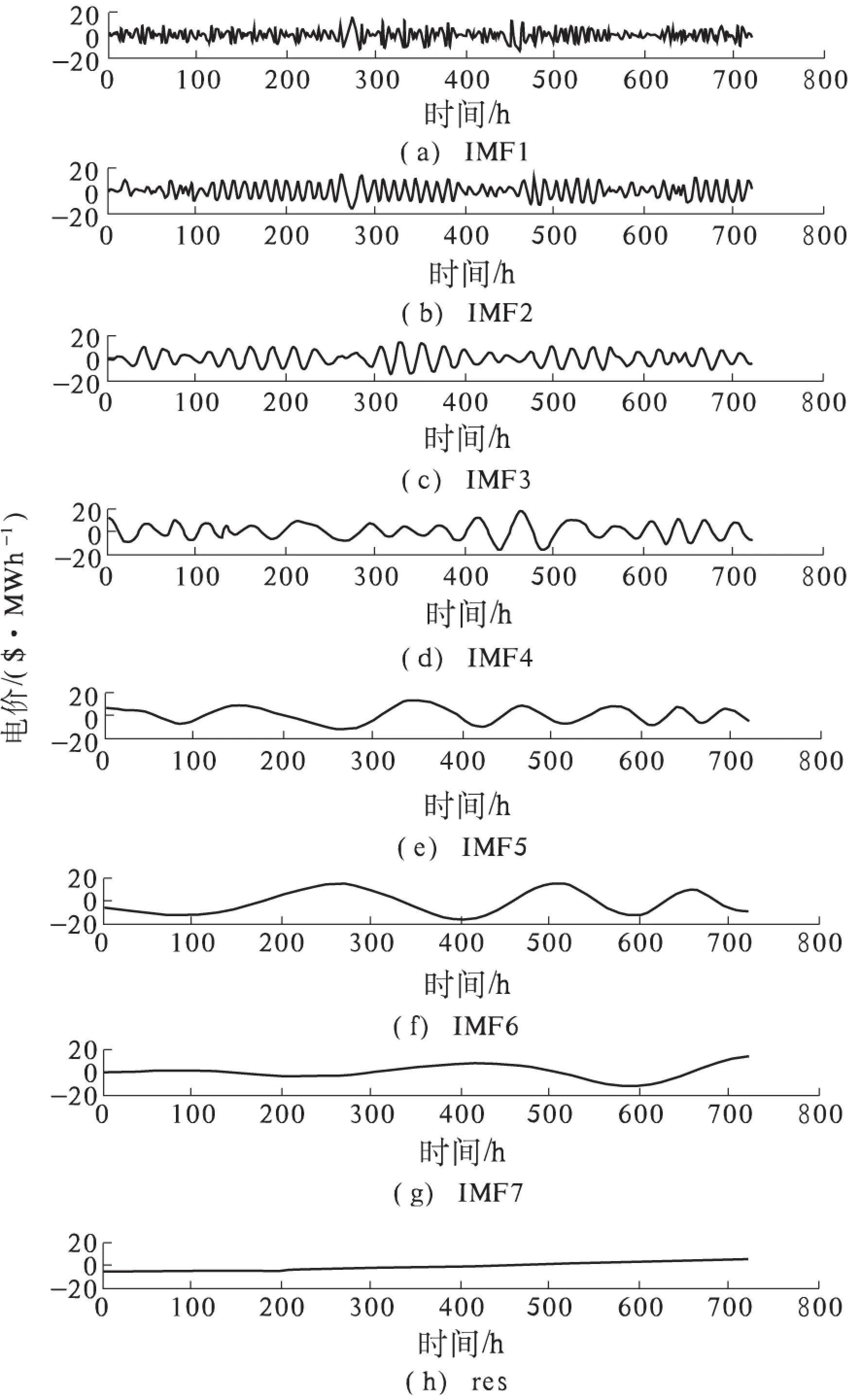
图1　EMD分解

将IMF1的组合预测模型、3个单一模型预测结果与实际电价IMF1分量进行对比分析，如图3所示，各模型预测结果的误差对比分析，如表2所示.

通过各个模型的误差对比分析，可知组合预测模型的精度均高于任一单一预测模型.然后对IMF2～IMF3，IMF4～IMF7分别采用LS-SVM、RBF神经网络模型进行预测.将各IMF分量的预测结果进行叠加得到最终10月31日24 h的电价预测结果.为了验证基于HHT组合预测方法的准确性，同时分别采用RBF神经网络、LS-SVM、粒子群算法单独预测并进行对比，对于粒子群算法设置最大迭代次数为1 000次，惯性权重选为0.6，加速因子c1=c2=2，精度为10-4，最终迭代次数为860次，各模型结果对比如图4所示.

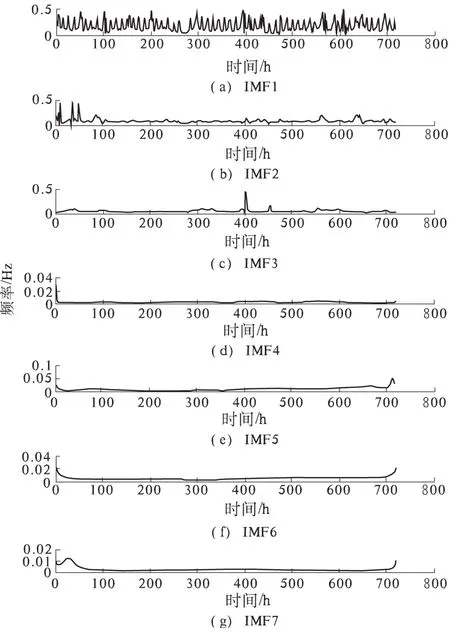
图2　IMF分量频谱

Hz

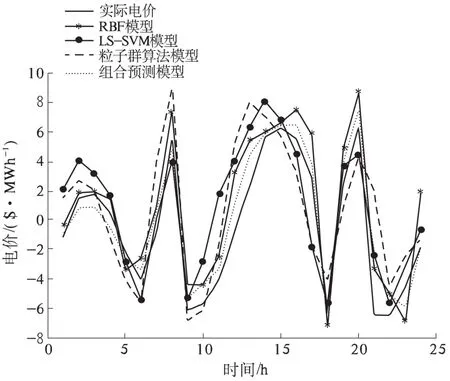
图3　IMF1各模型预测曲线

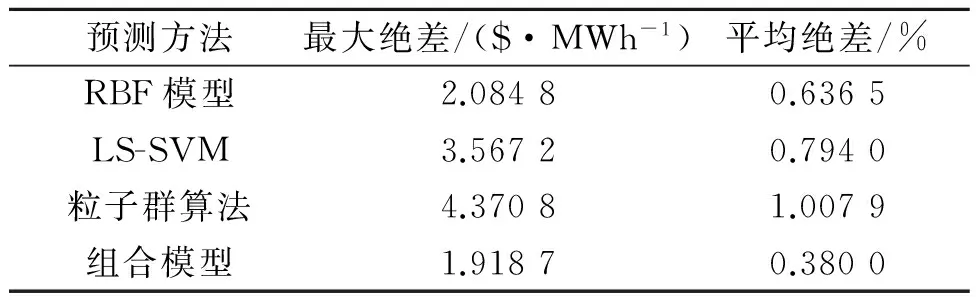
预测方法最大绝差/(S|·MWh-1)平均绝差/%RBF模型2.08480.6365LS-SVM3.56720.7940粒子群算法4.37081.0079组合模型1.91870.3800

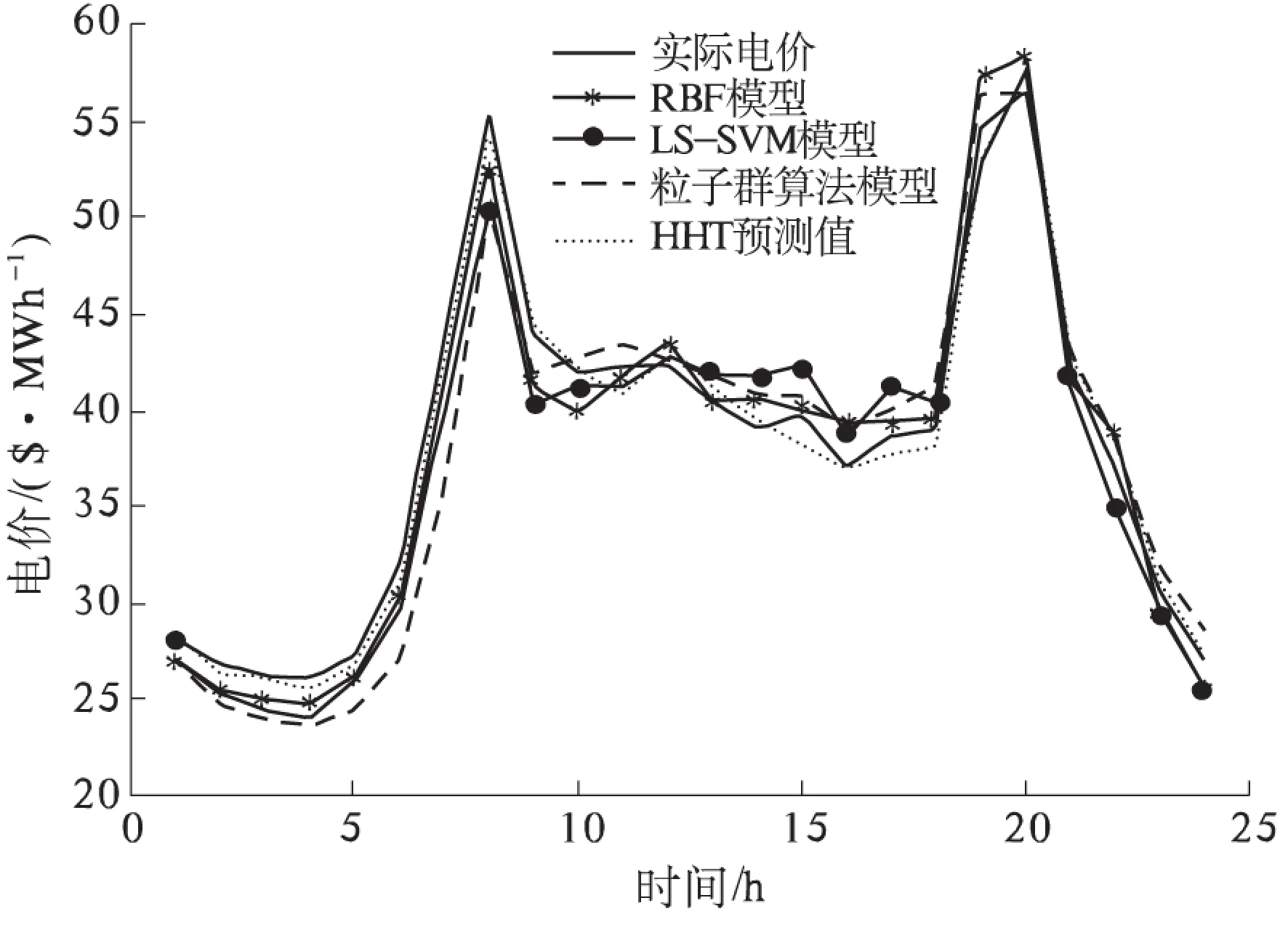
图4　预测结果对比图

采用平均绝对百分误差和最大绝对误差作为评价指标，表3给出了各模型的评价结果.从表3可以看出:基于HHT的组合预测最大绝对误差为1.53S|/MWh，平均绝对百分误差为1.61%，此方法在短期电价预测中精度均高于单一预测模型.

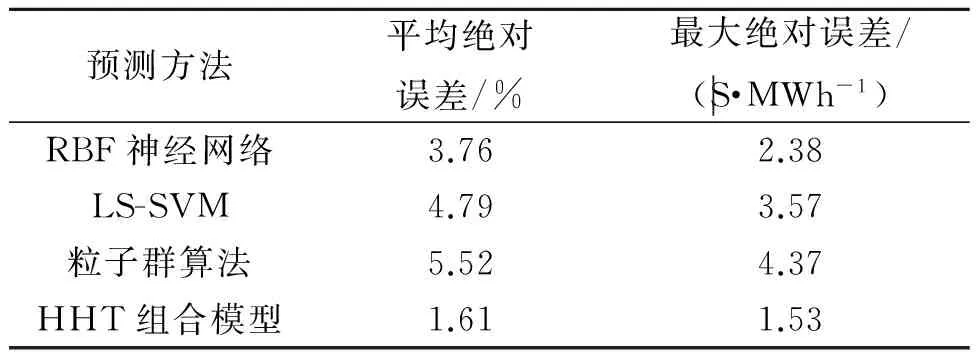
表3　评价指标结果

4结论

笔者提出基于 HHT的短期电价预测模型，将电价时间序列通过EMD分解为若干个IMF分量，针对各分量独有的频率变化情况分别采用不同的预测模型，对于高频分量采用组合预测模型，从而改善了高频分量的预测效果；对低频分量选择恰当的预测模型，将各分量的预测结果相加即为电价预测值.经过美国PJM电力市场日前实时电价数据进行验证，结果表明本研究预测模型具有较高的预测精度.

参考文献：

[1]张显，王锡凡．短期电价预测综述[J]．电力系统自动化，2006，30(3)：3-10．

[2]BENINI M，MARRACCI M，PELACCHI P，et al．Day-ahead market price volatility analysis in deregulated electricity markets [C] //Proceeding of IEEE PES summer meeting．Lllinois:Chicago，2002，45(3)：1354-1359．

[3]王瑞庆，李渝曾．含误差校正的粒子群优化 GM(1，2)短期电价预测方法[J]．电力系统保护与控制，2011，39(13)：54-59．

[4]师彪，李郁侠，于新花，等．自适应变系数粒子群和径向基神经网络在短期电价预测中的应用[J]．电网技术：2010，34(1)：34-39．

[5]黎特，皮薇．支持向量机模型改进及在短期边际电价预测中的应用[J]．国网技术学院学报：2013，16(5)：35-40．

[6]杨婵，舒崇军．基于神经网络的电力市场电价预测[J]．电气开关，2010，35(6)：35-41．

[7]ZHANG L，LUH P B，KASIVISWANATHAN K．Energy clearing price prediction and confidence interval estimation with cascaded neural networks[J]．IEEE Trans on power system，2003，18(1)：99-105．

[8]谭忠富，张金良．利用多因素小波变换和多变量时间序列模型的日前电价预测[J]．中国电机工程学报，2010，30(1)：41-46．

[9]牛丽肖，王正方．一种基于小波变换和ARIMA的短期电价混合预测模型[J]．计算机应用研究，2014，31(3)：16-22．

[10]毛玉龙，范虹．经验模式分解回顾与展望[J]．计算机工程与科学，2014，36(1)：156-161．

[11]丁倩．基于HHT的短期电力负荷预测研究[D]．郑州：郑州大学电气工程学院，2014．

[12]陈莺，徐晨，张维强．基于 Huang 变换和BP 神经网络的时间序列预测方法[J]．计算机工程与应用，2007，43(30)：242-244．

[13]王耀霞．基于Hilbert-Huang变换和最小二乘支持向量机的电力市场出清电价预测[J]．电子测量技术，2010，33(9)：39-41．

[14]Monthly Real-Time & day-ahead LMPs [B/OL]．(2013-06-10)[2014-09-01]．http：//www．pjm．com/．

[15]HUANG N E，SHEN Z，LONG S R，et al．The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis [J]． the Royal society of London series A，1998，454：903-995．

[16]POWELL M J D．The theory of radial basis function approximation in 1990，advances in numerical analysis II[M]．Oxford： Clarendon Press，1992：105-210．

[17]VAPNIK V N．An overview of statistical learning theory[J]．IEEE transactions on neural networks，1999，10(3)：988-999．

[18]KENNEDY J，EBERHART R．Particle swarm optimization[C]//Proceedings of IEEE international conference on neural networks IV．WA：Perth，1995：1942-1948．

[19]白玮莉，刘志刚，彭权威，等．基于HHT 和神经网络组合的负荷预测模型研究[J]．电力系统保护与控制,2009，37(19)：31-35．

A Method for Short-term Electricity Price Forecasting Based on HHT

LIAO Xiaohui1, ZHOU Bing1, YANG Dongqiang1, WU Jie2

(1.School of Electrical Engineering，Zhengzhou University，Zhengzhou 450001，China; 2.Zhengzhou Power Supply Company, Zhengzhou 450051，China)

Abstract:Short-term electricity price forecasting guarantees the maximum benefit of the parties involved in the power market.In view of the fact that the market clearing price has strong randomness and volatility, the paper proposes a combination forecasting model based on Hilbert-Huang transform. The price sequence is decomposed into a number of intrinsic mode function components and the remainder by using the empirical mode decomposition theory. Different models were built for each intrinsic mode function according to the size of each component’s average instantaneous frequency. Then the prediction results of each component are added up to obtain the final prediction value. And the model uses the actual data of PJM power market in the United States to test. Compared to the prediction results of any one sole model, this method accuracy were higher than single forecasting model, the maximum absolute error is 1.53 S|/MWh and the mean absolute percentage error is 1.61.

Key words:power market；electricity price forecasting；Hilbert-Huang transform；combined forecasting

收稿日期:2015-03-10；

修订日期：2015-06-19

基金项目：河南省科技厅国际合作项目(144300510009)

作者简介:廖晓辉(1972—)，女，湖北孝感人，郑州大学副教授，硕士，主要从事电力系统信号分析与处理研究，E-mail:liaoxiaohui0001@zzu.edu.cn.

文章编号:1671-6833(2016)01-0010-05

中图分类号：TM715

文献标志码：A

doi:10.3969/j.issn.1671-6833.201503041

引用本文：廖晓辉，周冰，杨冬强，等.一种基于HHT的短期电价组合预测方法[J].郑州大学学报(工学版)，2016，37(1)：10-14.