最小二乘复指数法在排气管试验模态分析中的应用

曾发林,许　凯

最小二乘复指数法在排气管试验模态分析中的应用

曾发林1,许凯2

(1.江苏大学 汽车工程研究院，江苏 镇江 212013； 2.江苏大学 汽车与交通工程学院，江苏 镇江 212013)

摘要：最小二乘复指数识别法(least squares complex method,LSCE),不仅适用于弱阻尼也适应于强阻尼密集模态识别.针对某轿车双排气管，采用LSCE法进行排气管试验模态分析，得到该排气管的模态分布比较密集的结论.试验表明，LSCE法对模态参数识别具有很强的适应性.

关键词：排气管；LSCE；试验模态；稳态图；参数识别

0引言

汽车排气管通过排气多支管与发动机相连，并通过吊挂件与车架或车身固定.由于汽车在行驶时受到路面谱等激励源作用，导致排气系统的振动较大.排气管吊悬装置的材料特性决定了其非线性，其固有频率偏高，中高阶振型与模态耦合严重[1].试验模态分析是研究汽车排气管动态特性的主要方法，现广泛应用最小二乘复指数法，根据极点的稳态图求固有频率和振型.笔者介绍了LSCE模态分析法，并进行排气系统的模态试验，对所测得的数据进行了分析，得到其固有特性.

1LSCE法介绍

最小二乘复指数法能够同时识别出不同模态的模态频率以及模态阻尼，并且对采集的数据进行同步分析并作出整体估计.冲激响应(IR)的表达式为

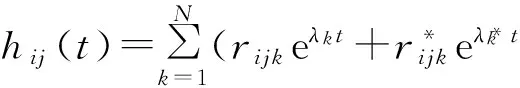
(1)

从式(1)可知,极点λk不是输入自由度或输出自由度的函数，而是反映结构的总体(而非局部)特性的函数.对于结构上的所有频响函数来讲，它们的极点值应该相同.因此应尽量测得结构的所有数据进行整体估计.

1.1针对连续模型

通过式(1)来实现上述的整体估计将会出现一个问题，即留数rijk与输入和输出有一定的关系[2].针对这种情况，需要找到一种新的参数模型来替代冲击响应函数hij，使得方程系数与输入和输出没有关联，并能够很好地识别系统的极点λk.可以由文献[2-3]证明，该参数模型的线性微分方程的形式为

(d/dt)2Nhij+a1(d/dt)2N-1hij+…+a2Nhij=0.

(2)

式(2)的主要作用是将数据变成一组复共轭对的有阻尼复指数的线性组合.这些复指数就是线性微分方程式(3)的特征解[2-3].

(d/dt)2Nf(t)+a1(d/dt)2N-1f(t)+

…+a2Nf(t)=0.

(3)

式(2)成立的条件：

λ2N+a1λ2N-1+…+a2N=0；

(4)

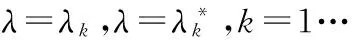
(5)

利用所测的数据估计出式(2)中的系数a1,a2,…，an，并求出方程(4)、(5)的解，得到复指数系数λk的值.

1.2针对非连续模型

对非连续模型，用式(6)、(7)计算较合适.

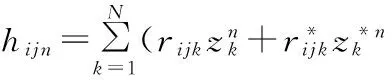
(6)

zk=eλkΔt.

(7)

式(6)、(7)用来取代有阻尼复指数，并用基函数zk来表示.与连续模型相似，在非连续模型中也需要找到一个常系数线性微分方程：

hijn+a1hijn-1+…+a2Nhijn-2N=0.

(8)

特征值zk可由下面的方程求出：

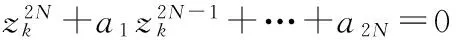
(9)

LSCE法主要利用所测的数据带入式(8)中求出其系数，并对极点进行估计.因此为了更好地对整体估计，尽量利用所有的数据频响函数hijn进行分析[3].

要对全部的时间点、响应和参考自由度在最小二乘上进行估计，需要求解方程(10)，该方程是强超定方程.利用二次系数矩阵组成的压缩方程可以求解该方程，式(11)为式(10)的简化形式.

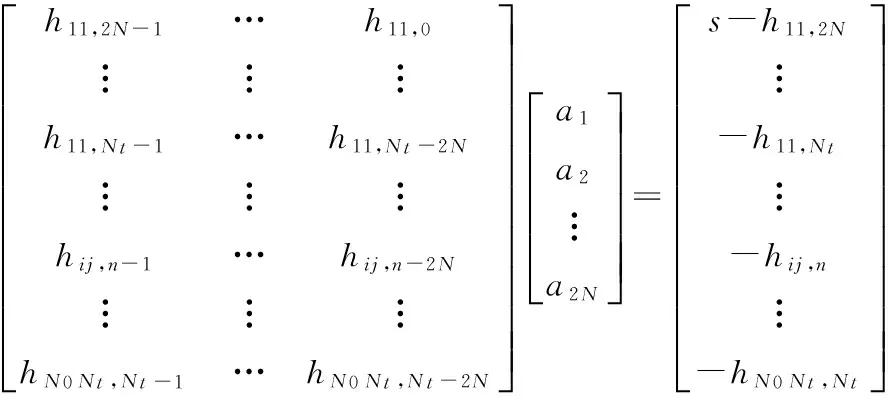
(10)

式中：Nt为最终可取得时间抽样；N0为响应自由度数.

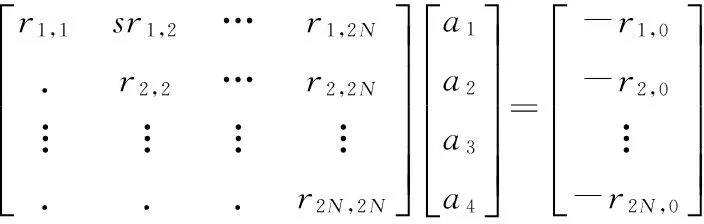
(11)

其中，协方差矩阵中的系数表示为

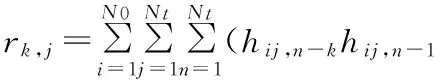
(12)

1.3最佳模态参数的确定

求出方程(11)中的解，就能够得到式(8)所表示模型中的系数最小二乘估计.相应的还能够求出最小二乘误差值，此误差对确定最佳模态数有很大的帮助.上述的推论中是基于数据中有N个模态存在的前提，但是实际数据中模态数量却是未知的.LSCE法通过最小二乘误差与假定模态数之间的变化关系来确定模型的真实模态情况，因此在建立方程(11)的时候，认为模态数N是足够大的.求解模型系数的方程中的每个解集就表示一个模态，方程如式(13)所示：

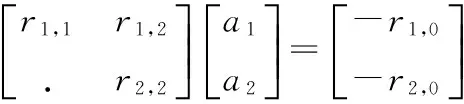
(13)

对应的最小二乘误差值用ε1表示.当假定的模态数与实际存在的模态数相同时，求出的最小二乘误差值将会比假定模态数与实际模态数相差很大时小很多[4].

为了得到准确的模态数，可以针对不同模态数的模型所评估出的阻尼及频率进行比较分析，真实的模态不会随假定模态数变化而变化.真实的模态应该是很稳定的.通过极点稳态图如图1所示，可以很好地分辨出模态数.其中，极点稳态图中的符号意义如表1所示.

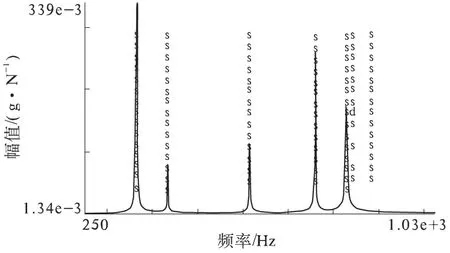
图1　极点稳态图

符号状态o极点不稳定f极点的频率在公差范围内稳定d极点的阻尼和频率在公差范围内稳定v极点向量在公差范围内稳定s极点的频率、阻尼、向量在公差范围内都稳定

2汽车排气系统仿真模型建立

2.1汽车排气系统的组成

排气系统一般指的是从与发动机相连的排气多支管开始至排气尾管结束之间的零件组合.排气系统大致包括以下几个部分：排气多支管、三元催化器、Y型管、波纹管、前置消声器、中间连接管、副消声器、挂钩、吊耳等.如图2所示为双排气管排气系统的结构图.排气系统一端通过排气多支管与发动机相连接，另一端通过挂钩吊耳与车架或者车身柔性连接.

2.2排气系统几何模型的建立

笔者研究的排气系统为双排气管，由三元催化器、柔性连接、消声器、连接管、吊钩、法兰和尾管组成,其基本结构如图3所示.其中在建模时，以汽车的前进方向为x轴，驾驶员的左手方向为y轴，垂直向上为z轴.

图2　双排气管排气系统的结构图

图3　双排气管排气系统的CATIA模型图

3排气管模态试验

模态试验是指通过试验的手段来获取模型或系统的固有特性，如模态频率、模态振型、模态阻尼等[5].笔者根据实际双排气管排气系统的实际模型进行约束模态试验.试验时，由于排气管的长度比较大，质量刚度分布不均，所以布置了50个激励点和12个3向传感器，即在x、y、z3个方向上的36个方向的响应.为保证试验的可靠与准确性，响应点和激励点均设置在刚度和质量比较大的地方.将排气管用4根非常柔软的弹性绳吊起，来模拟其自由的状态.所用的试验硬件设备为鲁文测试系统(leuven measurement & system,LMS).通过LMS进行了信号采集，利用LMS Test.Lab中的PolyMax进行模态提取与分析.各测点的传递函数试验数据获取时，需观察其信号相干性，相干系数在0.8以上的信号方能有效[6].

试验的系统主要由3大部分组成：试验激振系统、数据采集系统和模态处理系统.激振系统主要包含脉冲锤.数据采集系统包括：力传感器、加速度传感器和LMS信号采集系统[7].试验中所使用的测试和分析仪器设备如表2所示.实验安装与测试如图4所示.

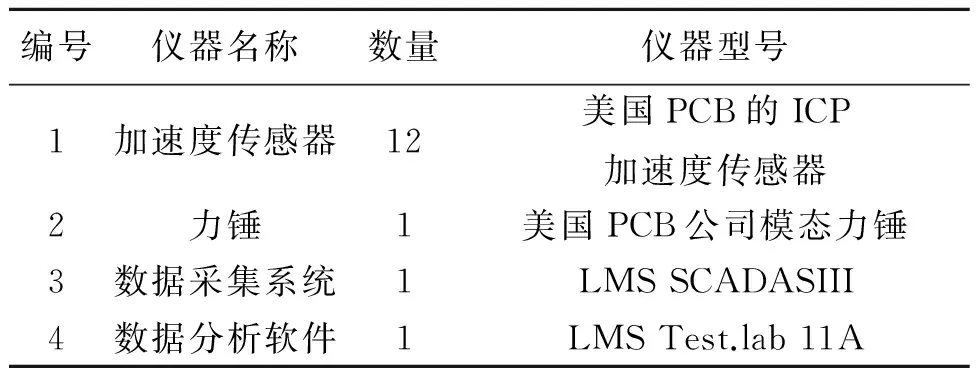
表2　试验仪器和设备

图4　排气管的自由模态试验安装与测试

4基于LSCE法对采样数据分析

对所采集的信号进行选择时，选取相干性较好的数据，得到的自由模态极点稳态图如图5所示.

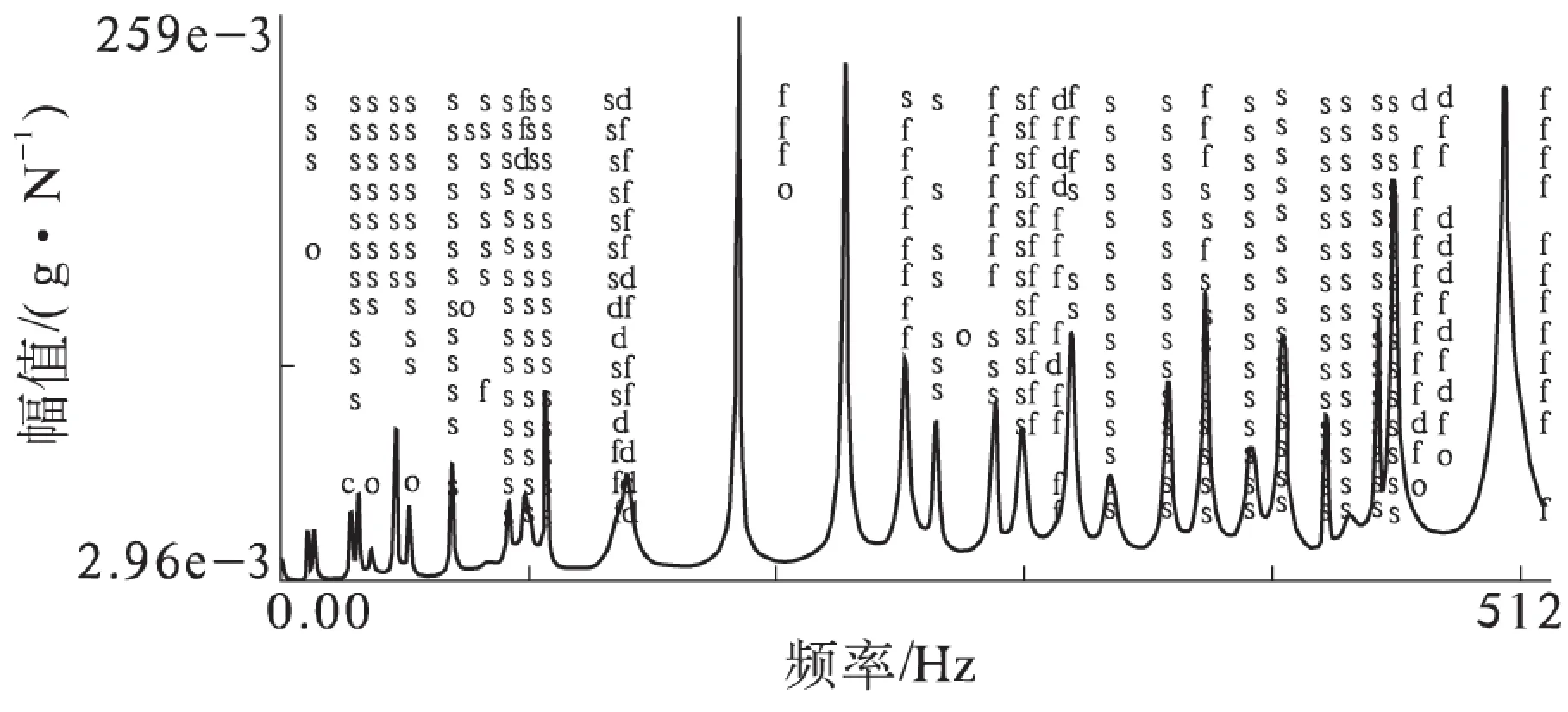
图5　极点稳态图

从图5中可以看出，排气管模态数较多，模态耦合严重，通过极点的稳定性能够轻易地分出固有频率[8].分析出的固有频率如表3所示，振型图如图6所示.由于篇幅有限，只列出了前六阶模态阵型图.

由上述得到的模态振型能够轻易地分辨出在对应固有频率处的振动情况.例如，在第五阶固有频率45.627 Hz处，排气管振动为沿着y法向的横向振动和绕着z轴的扭转耦合振动.可以通过一些技术手段，改变排气管以及吊耳刚度来调整系统的固有频率,使激励频率避开其固有频率，从而达到对排气系统减振降噪的效果[9-10].

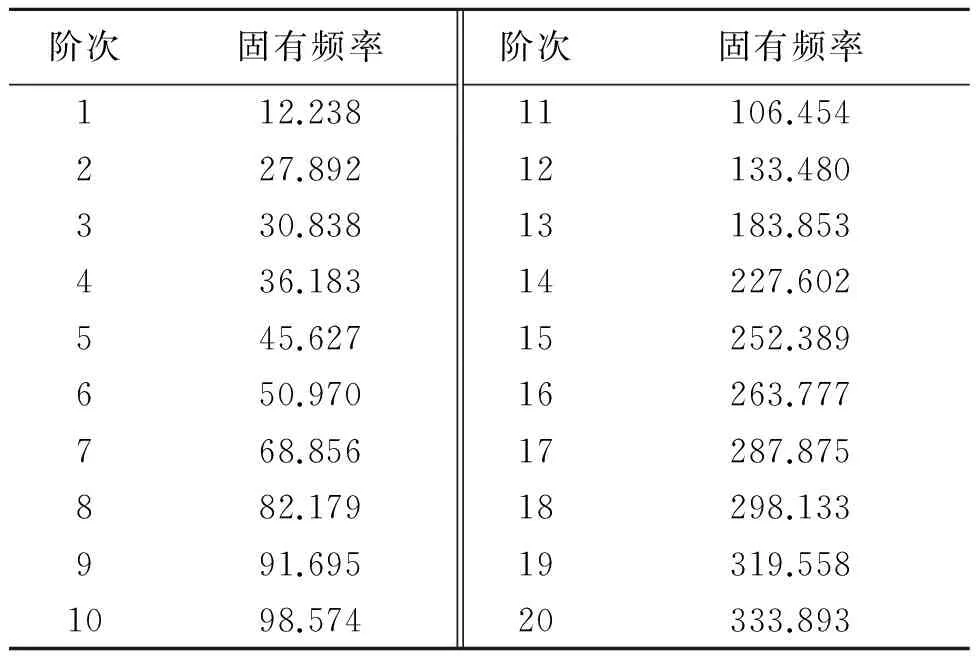
表3　试验自由模态频率表

图6　排气管前六阶模态振型图

5结论

笔者通过对某典型轿车的排气管进行自由模态分析，可知此排气管的模态分布比较密集，使用LSCE法对试验数据进行处理，分析表明，该方法能够更好地识别模态参数,具有较好的适应性和推广应用价值.

参考文献：

[1]张修路，姚国凤，韩春杨，等.汽车排气系统的悬挂点对减振效果的仿真分析[J].系统仿真学报, 2014,26(4):796-801.

[2]李德葆.实验模态分析及其应用[M].北京:科学出版社,2001.

[3]郑锦涛.车身试验模态分析方法对比研究[D].广州：华南理工大学机械与汽车工程学院，2012.

[4]魏传峰，周鋐，陈栋华，等.多参考最小二乘复频域法在轮胎试验模态分析中的应用[J]汽车技术，2006，23(10)：32-37.

[5]谢维波，林劲松.复指数信号模型非线性最小二乘解的几何结构及迭代算法[J]，电子学报，2002,30(5):757-759.

[6]谢小平，韩旭，吴长德，等.基于PolyMax方法的某轿车白车身试验模态分析[J].汽车工程，2009,31(5):440-443.

[7]庞剑，何华.汽车噪声与振动理论与应用[M].北京：北京理工大学出版社，2013.

[8]马维金,熊试波.基于LSCE算法和FDD算法的振动筛动态特性研究[J].振动、测试与诊断,2003,23(3):195-200.

[9]杨剑辉.结构阻尼时域识别方法的研究[D].武汉：武汉理工大学土木工程与建筑学院，2007.

[10]王卫华，杨转运，刘会.利用LSCE方法识别桥梁启动导数研究[J].试验流体力学,2009,23(1):85-89.

Application of the LSCE Method in the Exhaust Pipe Mode Analysis

ZENG Falin1, XU Kai2

(1.Automotive Engineering Research Institute, Jiangsu University, Zhenjiang 212013, China; 2.School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

Abstract:Identification method of least squares complex exponential LSCE (least squares complex method) is applied to both the weak and strong damping damping to identify the intensive modal. For a car dual exhaust pipes, exhaust pipe experimental modal has been to be analyzed by using LSCE method and the conclusion is drawn that modal distribution of the exhaust pipe is more intensive. The tests showed LSCE method has strong adaptability for modal parameter identification.

Key words:exhaust pipe; LSCE; experimental modal; steady chart; parameter identification

收稿日期:2015-03-08；

修订日期：2015-06-18

基金项目:江苏省高校自然科学研究资助项目(11KJA580001)

作者简介:曾发林(1965—)，男，江苏宜兴人,江苏大学副教授，硕士，主要研究方向为噪声与振动控制，E-mail:740369505@qq.com.

文章编号:1671-6833(2016)01-0045-04

中图分类号：U467.3

文献标志码：A

doi:10.3969/j.issn.1671-6833.201503034

引用本文:曾发林，许凯.最小二乘复指数法在排气管试验模态分析中的应用[J].郑州大学学报(工学版)，2016,37(1):45-48.