基于旋转波片的斯托克斯参量检测与精度分析

支丹丹， 李健军， 高冬阳， 袁银麟， 翟文超， 庞伟伟， 郑小兵*

1. 安徽大学物理与材料科学学院， 安徽 合肥 230031

2. 中国科学院安徽光学精密机械研究所通用光学定标与表征技术重点实验室， 安徽 合肥 230031

基于旋转波片的斯托克斯参量检测与精度分析

支丹丹1, 2， 李健军2， 高冬阳2， 袁银麟2， 翟文超2， 庞伟伟2， 郑小兵2*

1. 安徽大学物理与材料科学学院， 安徽 合肥 230031

2. 中国科学院安徽光学精密机械研究所通用光学定标与表征技术重点实验室， 安徽 合肥 230031

用于偏振光学遥感器定标的参考光源， 其偏振态的检测精度会直接影响偏振光学遥感器的定标精度， 进而影响目标特性的反演水平。 选用870 nm波段的水平线偏振光作为被测试的定标参考光源， 通过旋转1/4波片(quarter-wave plate, QWP)对其光强进行调制。 调制光强可表达为波片快轴旋转角度的傅里叶级数， 采用傅里叶变换法反演出级数的系数， 根据该系数即可计算出被测试光源的Stokes参量。 给出10次测量各参量及偏振度的平均值、 标准偏差、 合成不确定度以及测量平均值与理论值的相对偏差。 为提高测试精度， 通过对波片快轴初始定位角度偏差Δα、 延迟量偏差Δδ与检偏器透光轴角度偏差Δβ进行分析， 提出了偏差修正模型。 该模型通过Stokes参量检测偏差随Δδ和Δβ的变化趋势及实际偏差值， 确定Δδ和Δβ的大小。 结合模拟出的波片快轴初始定位角度偏差Δα， 对实验装置加以调整， 再次对光源的偏振态进行检测。 结果表明， 基于该修正模型测得光源的各Stokes参量与理论值最大偏差从未经修正的3.77%降低至1.41%。 证实了基于本实验的原理、 装置、 测量方法及所提出的偏差修正模型可有效提高定标参考光源偏振态检测的精度。

定标参考光源； Stokes参量检测； 偏差修正； 分析仪； 偏振

引 言

为实现目标的全Stokes参量偏振成像， 除选择位于大气窗口的近单色波段作为探测通道外， 还需要具有较高检测精度的偏振光学遥感器。 为了获得高精度的偏振观测精度， 需要对偏振光学遥感器开展高精度的实验室定标， 利用偏振态已知的参考光源是偏振定标的常用手段之一。 偏振态定标参考光源的校准精度将直接影响到偏振光学遥感器的定标精度， 并影响到目标特性反演精度水平。

光源Stokes参量检测方法主要有分振幅法和偏光调制法。 分振幅法是将光束分为4束， 用四个探测器同时完成对某一瞬时各Stokes参量的测量[1]。 偏光调制法是指在光路中引入相位调制器， 通过测量调制光强求得Stokes参量[2]， 包括旋转波片法、 干涉调制法[3]、 弹光调制法[4-5]、 带调制器(电光、 声光、 磁光)的偏振光计[1]等。

通过旋转1/4波片来实现对光强的调制， 出射光强信号可表达为波片快轴旋转角度的傅里叶级数。 根据傅里叶变换法， 级数的系数可表达为出射光强对旋转角度的积分， 最后采用辛普森法计算积分表达式求出级数的系数， 通过该系数可求出Stokes参量和偏振度。 旋转波片法具有装置简单、 结构稳定且适用于连续光波测量等优点[6]， 辛普森算法即抛物线法， 在测量点数有限的情况下， 对积分表达式的计算精度优于矩形法与梯形法。

利用光谱偏振分析仪对水平线偏振光的偏振态进行分析和检测， 求出各Stokes参量与偏振度的平均值、 标准偏差和合成不确定度。 光谱偏振分析仪主要由1/4波片、 检偏器和探测器组成。 波片相位延迟量偏差Δδ、 快轴初始定位角度偏差Δα与检偏器透光轴角度偏差Δβ是影响基于旋转波片法的Stokes参量检测的主要影响因子[7-8]。 因此， 对波片相位延迟量的精确测量、 快轴初始定位角度与检偏器透光轴角度的精确校准尤为重要。 分析了Δδ， Δβ对Stokes参量和偏振度偏差的影响变化趋势， 根据测量值与理论值偏差， 确定了Δδ， Δβ的大小。 结合模拟出的波片快轴初始相位偏差并在算法公式中加入初始相位， 采用修正后的波片相位延迟量并调整检偏器透光轴角度， 再次对光源的偏振态进行检测。 将修正后的结果与未经修正的结果进行对比分析。 结果表明， 基于该修正模型测得光源的各Stokes参量与理论值最大偏差从未经修正的3.77%降低至1.41%。

1 Stokes参量求解

图1 Stokes参量测量装置

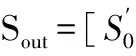
(1)

将该式展开成傅里叶级数形式[9]， 即

(2)

通过傅里叶变换， 得出变换系数分别为

(3)

通过反演得到任意偏振态光源Stokes参量[S0，S1，S2，S3]-1与β，δ之间的关系为

(4)

偏振度P可表示为

(5)

合成不确定度可表示为

(6)

u代表S0，S1，S2，S3或P。

通过式(1)可知， 旋转波片或偏振片都可起到对光强的调制作用。 因为光电探测器的光敏面基本上都具有一定的偏振敏感性， 旋转偏振片会改变入射到光敏面上光束的偏振态， 可能引起较大偏差， 因此实际测量时以旋转波片固定偏振片为佳。 由式(4)可知， 求Stokes参量的关键在于精确求解系数A，B，C，D或E。 为便于使用离散测量值进行数值计算， 采用辛普森方法[10]将式(3)的积分表达为求和形式

(7)

其中，Y代表被积函数，M代表系数A，B，C，D或E，N为测量点数，l=N/2。

2 实验部分

2.1 Stokes参量检测装置

实验中采用美国Coherent公司生产的MBR-110钛宝石激光器， 光源中心波长为870 nm， 线宽为2.7×10-7nm。 偏振片的消光比为105， 采用的波片为胶合零级波片， 起偏器与1/4波片可构成任意偏振态发生器。 产生的偏振光由光谱偏振分析仪检测， 其主要构成元件有1/4波片、 检偏器和陷阱探测器， 仪器的视场角低于±1°。 实验装置图如图1所示。

起偏器和检偏器透光轴固定在水平方向， 两个1/4波片分别固定在定位精度为0.05°的电控旋转台上， 由步进电机控制器控制旋转。 1/4波片1透光轴与x轴夹角为某一固定值时， 可产生特定偏振态的偏振光。 1/4波片2用来实现对光强的调制。 实验中电控旋转台每隔6°旋转一次， 旋转范围为0～360°。 调制光经过检偏器后再由具有良好的线性、 稳定性、 消杂散光特性和极低的偏振敏感性的陷阱探测器[11]接收， 转换为电信号输入计算机， 由计算机进行数据处理与分析。

2.2 数据采集

水平线偏振光的理论光强采集曲线如图2中红色实线所示， 黑色方框代表实验数据采集点。

图2 水平线偏振光的理论与测量光强随

Fig.2 Theory and measured intensities as a function of the angleαof QWP fast axis withxdirection for a horizontal linear polarized input beam

为了评估采样点的准确性， 采用皮尔森相关系数r来评估测量数据与模拟数据之间的吻合度。r可表示为

(8)

式(8)中，xi为实验测量值，yi为理论值，i的取值范围为1～60。r值越大表示二者相关性越强， 测量值的准确度越高。 多次测量结果表明r>0.998， 说明实际测量值与理论值符合较好。

3 结果与讨论

表1给出了水平线偏振光各Stokes参量与偏振度P的理论值、 测量平均值， 标准差及合成不确定度， 表中数据为10次测量计算结果。 测量平均值与理论值相比， 各参量测量偏差除S2分量为3.77%， 其余均在0.5%以内， 偏振度测量偏差为0.02%。

从表1可以看出，S0，S1分量合成不确定度较为接近而S2，S3分量合成不确定度相对较小， 原因在于所测量偏振光为线偏振光， 圆偏振分量几乎为0， 所以S3分量合成不确定度较小。S2分量相对较大， 测量偏差达到3.77%， 即有非水平线偏振光被探测器所接收。 采用以下方法提高测量精度： (1)采用具有较高消光比的起偏器与检偏器； (2)实验前应对起偏器透过轴方向精密校准； (3)实验时应确保在黑暗环境中进行， 避免杂散光入射到实验装置中。

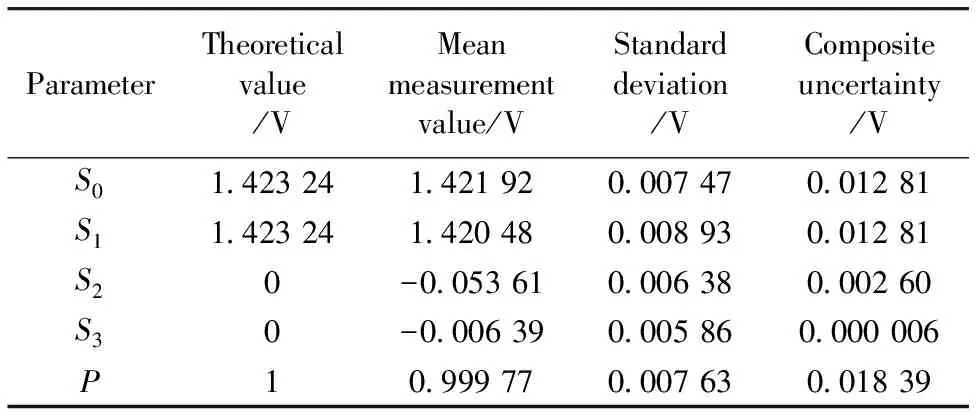
表1 水平线偏振光测量结果

3.1 影响因子α及修正方法

波片快轴初始定位方向为水平方向， 定位角度存在偏差， 在波形上表现为任意偏振态的入射光光强波形曲线相对理论曲线有一定的相位移动。 为消除相位移动对参量检测的影响， 数据处理时先对测量光强值进行拟合求出初始相位， 再在式(7)中加入初始相位进行计算。

将10次采集原始数据求平均值， 然后对曲线进行拟合。 从拟合结果看， 所采集曲线与理论曲线有-3.87°的相位移动， 将式(7)算法公式中加入初始相位， 得修正后的各参量值如表2所示。

表2 经Δα修正后各偏振参量值

表2给出了经相位修正后各参量的平均值、 合成不确定度及相对未经修正时测量值提高精度。 可以得出， 各Stokes参量测量值与理论值偏差均小于2.98%， 偏振度偏差小于0.01%。 各参量合成不确定度相对未校准时均有所下降。 表2中数据仅是进行相位修正后的结果。

3.2 影响因子δ，β及修正方法

式(4)给出了波片的相位延迟量δ、 检偏器透光轴角度β与各参量及偏振度之间的关系。 算法式(7)中隐含了波片快轴初始定位方向为水平方向， 即采集曲线初始相位为0。 因此需要在对波片快轴初始定位角度进行修正的基础上， 再对波片的相位延迟量δ、 检偏器透光轴角度β进行修正。 将式(4)中δ改写为δ=Δδ+90°， Δδ为延迟量偏差，β=Δβ， Δβ为检偏器定位角度偏差， 可得各参量理论值与实际值之间的差值ΔS随Δδ， Δβ变化关系图如图3所示(取Δδ范围为±1°， Δβ范围为±0.5°)。

图3 水平线偏振光Stokes参量及偏振度测量偏差随Δδ和Δβ变化趋势图

由图3可知水平线偏振光各参量及偏振度的相对偏差随Δδ， Δβ的变化趋势。 在Δδ=±1°， Δβ=±0.5°范围内， ΔS0随Δδ， Δβ的增大而增大； ΔS1与ΔP随Δδ， Δβ的增大而减小； ΔS2随Δδ的增大而增大， 随Δβ的增大而减小。 对ΔS3而言， Δδ， Δβ偏离0值越大， ΔS3越大。 通过以上变化趋势及实验测量值与理论值之间的差值， 可确定Δδ， Δβ的大小。 Δδ、 Δβ及Δα为影响参量检测的主要影响因子， 根据偏差大小对实验装置加以调整并对影响因子进行修正， 即可测量出较为精确的Stokes参量。

同时由图3可以看出Δδ对ΔS0、 ΔS1及P的影响较大， Δβ对ΔS2及ΔS3的影响较大。 由表1可知， 未经修正时S2的测量偏差相对其他因子较大， 可推断出检偏器定位角度偏差相对较大； ΔS0， ΔS1及P测量偏差较小， 可推断出Δδ相对较小。 选取ΔS1变化趋势图， 根据理论值与实际测量值求出ΔS1=-0.002 35 V， 可唯一确定Δδ=0.09°， Δβ=-0.45°。 根据Δβ的大小调整检偏器， 将修正后的相位延迟量重新代入式(4)中， 并将式(7)中加入初始相位， 得修正后各参量测量值如表3所示。

从表3可知， 经Δδ， Δβ及Δα修正后， 各Stokes参量S0，S1，S2，S3与P测量值与理论值偏差分别为0.02%， 0.28%， 1.41%， 0.40%与0.29%。 相对未经修正时各参量测量精度除S1和P分量略有下降外， 其余分量测量精度均有所提高，S2分量提高精度较大， 达到2.36%。 测量合成不确定度相对未校准时也有所下降， 在一定程度上验证了修正方法具有可行性。

表3 经Δδ， Δβ及Δα=-3.87°修正后各偏振参量值

Table 3 The measurement results of Stokes parameter after Δδ， Δβand Δα=-3.87° correction

ParameterMean/V CompositeUncertainty/VImprovedPrecision/%S01 423560 012310 07026S11 419230 01241-0 08773S20 020040 002502 35870S3-0 005650 00000020 05199P0 997090 01731-0 26800

4 结 论

通过对基于旋转波片法Stokes参量测量原理的分析， 得出测量偏差与波片的快轴初始定位角度及波片相位延迟量、 检偏器透光轴角度之间的变化关系， 提出了Stokes参量测量偏差修正模型。 该模型通过数据采集曲线的初始相位来确定波片快轴初始定位角度偏差Δα的大小， 通过各参量测量偏差与波片相位延迟量偏差Δδ、 检偏器透光轴角度偏差Δβ的变化趋势确定了Δδ、 Δβ的大小。 调整检偏器透光轴角度、 在算法公式中加入初始相位及采用修正后的波片相位延迟量后对定标参考光源重新进行数据采集， 结果表明， 经修正后测得的定标参考光源各Stokes参量与理论值最大偏差从未经修正的3.77%降低至1.41%。

[1] LIAO Yan-biao(廖延彪). Polarization Opitics(偏振光学). Beijing： Science Press(北京： 科学出版社), 2003.

[2] CHENG Min-xi, HE Zhen-jiang, HUANG Zuo-hua(程敏熙， 何振江， 黄佐华). Opto-Electronic Engineering(光电工程), 2008, 35(5): 93.

[3] ZHU Bao-hui, ZHANG Chun-min, JIAN Xiao-hua, et al(祝宝辉， 张淳民， 简小华， 等). Acta Physica Sinica(物理学报), 2012, 61(9): 090701.

[4] GAO Ting-ting, HAN Hui-lian, ZHANG Rui, et al(高婷婷， 韩慧莲， 张 瑞， 等). Opto-Electronic Engineering(光电工程), 2013, 40(3): 113.

[5] LI Zhi-cheng, TANG Zhi-lie, CHEN Ping, et al(李志诚， 唐志列， 陈 萍， 等). Acta Optica Sinica(光学学报), 2012, 32(5): 0512005.

[6] Flueraru C, Latoui S, Besse J, et al. Instrumentation and Measurement, 2008, 57(4): 731.

[7] TANG Fei-long, LI Zhong-liang, BU Yang, et al(汤飞龙， 李中梁， 步 扬， 等). Chinese Journal of Lasers(中国激光), 2013, 40(4): 0408006.

[8] Giudicotti L, Brombin M. Appl. Opt., 2007, 46(14): 2638.

[9] Berry H G, Gabrielse G, Livingston A E. Appl. Opt., 1977, 16(12): 3200.

[10] Tongji University, Department of Mathematics(同济大学数学系编). Highter Mathematics(高等数学). Beijing： Higher Education Press(北京： 高等教育出版社), 2007. 229.

[11] YUAN Yin-lin, ZHENG Xiao-bing, WU Hao-yu, et al(袁银麟， 郑小兵， 吴浩宇， 等). Acta Optica Sinica(光学学报), 2014, 34(12): 1223001.

*Corresponding author

Stokes Parameter Detection and Precision Analysis Based on Rotating Quarter-Wave Plate

ZHI Dan-dan1, 2, LI Jian-jun2, GAO Dong-yang2, YUAN Yin-lin2, ZHAI Wen-chao2, PANG Wei-wei2,ZHENG Xiao-bing2*

1. School of Physics & Material Science, Anhui University, Hefei 230031, China

2. Key Laboratory of Optical Calibration and Characterization, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China

The accuracy of the calibration reference source polarization states directly influences the precision of the polarized optical remote sensor calibration, and thus affects the inversion accuracy of the characteristics of targets. In this paper, 870 nm horizontal linear polarized light has been chosen as the tested calibration reference light, modulated by rotating quarter-wave plate(QWP). The intensity as a Fourier series of the rotation angle of the plate and its coefficients were demodulated with the Fourier transform method, Stokes parameters can be calculated with these coefficients. The mean, standard deviation, composite uncertainty and relative deviation of measured data compared with the theoretical value of the ten measurement results were presented. In order to improve the accuracy of the measurement, the correction model for the quarter-wave plate retardance deviation Δδ, fast axis angle deviation Δαand the transmission axis alignment deviation Δβof analyzing polarizer has been constructed. In this model, detection deviation of Stokes parameters is described as a function of Δδand Δβ, Δδand Δβwere determined by the function and magnitude of the deviation. Combined with quarter-wave plate fast axis angle deviation which was the result of simulation to adjust the experiment device, and then detecting the calibration reference source polarization states again. The experimental results show that, the difference between measured value and theoretical value of Stokes parameters reduced to less than 1.41% from 3.77% relative to without correction. The experiment principle, device and deviation correction model of this research can significantly improve the accuracy of detecting the polarization state of the calibration reference light source.

Calibration reference light source; Stokes parameter detection; Deviation correction; Polarimeter; Polarization

Jul. 24, 2015; accepted Nov. 30, 2015)

2015-07-24，

2015-11-30

国家(863)计划项目(2015AA123702)和国家自然科学基金项目(11204318)资助

支丹丹， 1989年生， 安徽大学物理与材料科学学院硕士研究生 e-mail: 15155181602@163.com *通讯联系人 e-mail: xbzheng@aiofm.ac.cn

O436.3

A

10.3964/j.issn.1000-0593(2016)08-2655-05