由一道例题引发的思考
2016-06-14吴云飞
◇吴云飞
由一道例题引发的思考
◇吴云飞
人教版教材四年级下册第10页有这样一道例题(如图1),其解决方法如图2所示。

图1

图2
新教材把它作为问题解决内容放在四则运算后面,其主要原因可能有两点:一是让学生运用四则运算法则解决问题,提高其计算能力和解决问题的能力;二是渗透优化思想,培养学生合理、灵活思考问题的能力。学完以后,学生能够想到的基本就是“尽量坐人均价格低的”和“尽量坐满”这两个条件。当然,这两个条件是至关重要的,这是统筹、优化思想的主要体现,在这方面学生已经在四年级上册的“烙饼问题”和“统筹安排”中研究过。
再看另一个“租船问题”(如图3)。
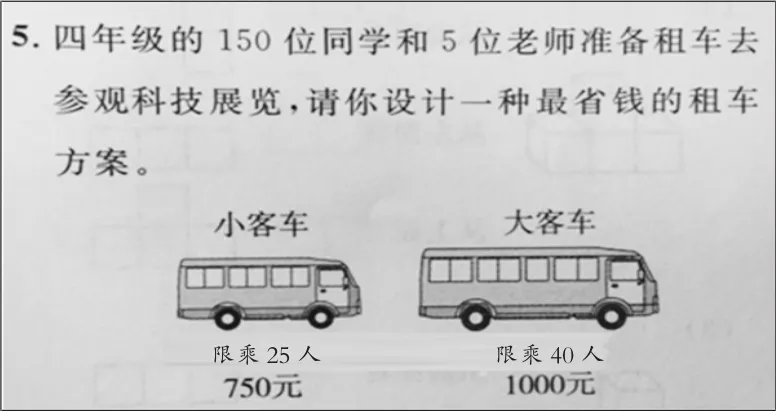
图3
考虑“尽量坐人均价格低的”和“尽量坐满”这两个条件,用2辆大客车和3辆小客车应该最省钱。实际情况是这样吗?该用什么方法解决呢?
在三年级教材上册中出现了这样一道例题(如图4)。

图4
这道例题其实就是“租船问题”的前身,其解决方法是列表法。
受此启发,可以考虑用列表法解决图3中的问题。
大客车每个座位25元,小客车每个座位30元。
(150+5)÷40=3(辆)……35(人),3+1=4(辆)。

表1
显然这里正好坐满并不是最省钱的,像这样的题目和生活例子还有很多。如果按照图2所示的方法解决这个问题,就很容易陷入“最好的方法是同时满足两个条件”的误区,从而出现遗漏“4 大0小”的情况。
为什么会出现这样的矛盾呢?笔者认为,它跟实际的“人均价格”有着紧密的联系。例如,75人打算租车去旅游,有图3所示问题中的两种客车可供选择,这时,选择2辆大客车,有空位,实际的“人均价格”为2000÷75≈27(元);选择3辆小客车,没有空位,实际的“人均价格”为2250÷75=30(元)。显然,用2辆大客车更省钱。也就是说,有时即使“用大客车会出现空位”,其实际的“人均价格”也会比“用小客车没空位或空位较少”要低。如果总共有145人,租3辆大客车和1辆小客车正好坐满,这是最省钱的租车方案。这里面似乎有一个“临界点”,笔者试图找到这个“临界点”。现固定图3所示问题中车辆的收费标准和载客量,试着探讨一下。

表2
分析表2中加粗的数据,发现它们无外乎以下几类:“小客车载客量的整数倍+1(如26、51等)”“大客车、小客车载客量的整数倍的和+1(如66、91等)”和“大客车载客量的整数倍+1(如41、81等)”。这似乎就是“临界点”。是否所有的“租船问题”都有类似的“临界点”呢?现固定图1所示问题中船只的收费标准和载客量,探讨该问题中是否存在类似的“临界点”。经验证,确实存在类似的“临界点”。当然,即使一个结论在许多情况下都成立,也不能说明该结论在所有情况下都成立,但这是探索的开始,是一个方向,从特殊到一般也是研究数学问题的一种重要方法,所以值得尝试。这个结论有待大家一同验证。
当然,学生不需要理解这么深。但是,对于“租船问题”,也绝非仅知道上面提及的“两个条件”就可以了。笔者认为,用列表法解决“租船问题”,在不失上述能力培养的同时,能更好地体现思维的严密性。那么列表法是如何体现思维严密性的呢?可以先从实际的“人均价格最低”入手,这就遵循了统筹、优化思想的第一原则,再考虑座位数,就可以达到策略最优化的目标了。解决问题的方法很多,但是作为教师,要熟知不同方法的不同价值,这样才能发挥每种方法的最大作用,其实这也是统筹、优化思想的体现。
(作者单位:浙江海盐县向阳小学)
