关于亚循环2-群的对合交换图
2016-06-12谭延庆沈如林
谭延庆,沈如林
(湖北民族学院 数学系,湖北 恩施 445000)
关于亚循环2-群的对合交换图
谭延庆,沈如林
(湖北民族学院 数学系,湖北 恩施 445000)
摘要:对合交换图是以群中二阶元共轭类为顶点,两顶点有边当且仅当它们交换的图.分类了亚循环2-群的对合交换图结构
关键词:对合交换图;k-正则图;亚循环2-群
设G是群,且X是G的子集,X上的交换图ΓG(X)是指以X中元为顶点,互异点x,y∈X有一条边当且仅当xy=yx.交换图被很多学者所研究,最早出现在Brauer和Fowler的文献[1]中,他们应用交换图证明了在同构意义下对于一个给定的2阶中心化子的同构型,只有有限个非交换单群包含该同构型.当X取成G{1}时,交换图ΓG(X)对Margulis-Platanov猜想的证明起到重要的作用[2].如果取X为G的一个二阶共轭类,称交换图ΓG(X)为对合交换图.Fischer最早对对合交换图进行了研究[3-4],考虑了3-轮换群生成的群,研究了一类任意两个顶点之积的阶至多为3的对合交换图的群的结构.Bates,Bundy,Hart 和Rowley关于对合交换图的文章使对合交换图越来越备受关注.文献[5-8]中分别全面研究了G为散在单群,G为有限Coxeter群,G为对称群和G为特殊线性群时对合交换图ΓG(X)的结构.本文分类了亚循环2-群的对合交换图的结构.所谓亚循环2-群即循环2-群对循环2-群的扩张.称图ΓG(X)为正则图,如果ΓG(X)中每个顶点所连的边数都相同.如果正则图中每个顶点相连的边数为k,则称为k-正则图.特别,0-正则图称孤立点图.以下的群都为有限群.
定理1亚循环2-群的对合交换图为一个点的孤立图或1-正则图.
1一些引理
如下给出一些引理:
引理1 设G为偶阶群,则G的对合交换图是一个正则图.
证明设X为G的一个二阶共轭类,并设ΓG(X)为对合交换图.假设a∈X,g∈G.如下考虑顶点a和ag的边数.设与a相连的顶点为ag1,ag2,…,agr. 若a与agi相连,即aagi=agia⟺[a,agi]=1⟺[a,agi]g=[ag,agig]=1⟺agagig=agigag,则a与agi相连推出ag与agig相连.现在从与a相连的边构造一个到与ag相连的边的一个映射σ:(a,agi)→(ag,agig),则由如上知道σ为一个单映射.下证σ是一个满映射.如果还有ah与ag相连,即[ag,ah]=1⟺[ag,ahg-1g]=[a,ahg-1]g=1有[a,ahg-1]=1这样存在某个gi使得hg-1=gi,故h=gig,这样σ是满射,即而为双射,从而ΓG(X)为正则图.
引理2 若2-群中的对合交换图为孤立点图,则它只能为一个孤立点的图.
证明设X为2群G的一个2阶共轭类,ΓG(X)为孤立点图,并设a为ΓG(X)的顶点.现在让〈a〉共轭作用在X上,由于ΓG(X)为孤立点图,则X的个数必然为奇数.另一方面,由于X为G的一个共轭类,则X的个数必然为2的幂,这样X的个数必然为1,即ΓG(X)只有一个孤立点.
引理3设r≠±1且r2m≡1(mod 2n),其中m≥1,n≥3,则当m=1时,(r-1)≡0(mod 2)或(r-1)≡0(mod 2n-1);m>1时,r2m-1-1≡0(mod 2n-1).
证明m=1时,r2m-1≡0(mod 2n)⟹(r-1)(r+1)≡0(mod 2n)⟹(r-1)/2·(r+1)/2≡0(mod 2n),(r-1)/2和(r+1)/2为连续数一奇一偶,若(r+1)/2为奇数,则(r-1)≡0(mod 2n-1);若(r+1)/2为偶数,则(r-1)≡0(mod 2).m>1时,r2m-1≡0(mod 2n)⟹(r2m-1-1)(r2m-1+1)≡0(mod 2n),(r2m-1+1)/2恒为奇数,故r2m-1-1≡0(mod 2n-1).
2定理1的证明
由文献[9]可知亚循环2-群的定义关系式为:
情形1t=0,r=-1.此时有a2n=1,b2m=1,ab=a-1.由b-1ab=a-1得:ab=ba-1,ba=a-1b.因为o(b2m-1)=2,a2n-1为2阶中心元,此时亚循环2-群存在二阶元共轭类.
(b2m-1)={b2m-1,(b2m-1)a,(b2m-1)a2,…,(b2m-1)a2m-1.下面分两种情况来讨论:
1)m=1.此时亚循环2-群为二面体群.b2=1,b={b,ba,ba2,…,ba2n-1-1}.由ba=a-3a-1b=a-4b;ba3=a-1a-4ba=a-5a-1b=a-6b;…;bai=a-2ib,0≤i≤2n-1-1.
假设bai=baj(0≤i,j≤2n-1-1),即a-2i=a-2j⟺a2(i-j)=1.则2(i-j)≡0(mod2n),也即(i-j)≡0(mod2n-1).由i,j的取值范围可知,不存在这样的i,j使得上式成立,故可知:b={b,ba,ba2,…,ba2n-1-1}中2n-1个元互异,类长为2n-1.
再设bbai=baib,由bai=a-2ib,ba=a-1b可得,ba-2i=a-2ib,也即:a4i=1(0≤i≤2n-1-1),故4i≡0(mod2n)⟺i≡0(mod2n-2).i可取2n-2,结合引理1得到:共轭类b中元每两个相连.
再来看亚循环2-群所有二阶元有哪些.m=1,群中所有元的形式只有ai,aib(0≤i≤2n-1)两种.a2n-1为中心二阶元,只需找aib形式的二阶元.而aibaib=aia-ib2=1,也即所有aib(0≤i≤2n-1)形式的元都为二阶元,共2n个.接下来再看一下这2n个二阶元所属共轭类情况.aib(0≤i≤2n-1)的共轭形式只有(aib)akb,(aib)ak两种.
若(aib)=a-1b,ab=ba-1化简可得到a2k-i-j=1,故有2k≡i+j(mod2n).根据i,j,k的范围,显然,当i,j的奇偶性不同时,它们就不可能共轭.i,j奇偶性相同时,总可以找到k=(i+j)/2使得:(aib)akb=ajb.
若(aib)ak=ajb(0≤i,j,k≤2n-1),即a-kaibak=ajb,化简得a2k+j-i=1,即2k≡i-j(mod2n).只需考虑i>j的情况,同样是当i,j奇偶性相同时,总可以找到相应的k=(i-j)/2,使得(aib)ak=ajb.综上所述,二面体群所有二阶元被分成两个共轭类,即奇数形式和偶数形式的共轭类,长度都为2n-1.且当i,j奇偶性相同时,由aibajb=ajbaib⟺a2(i-j)=1⟺i≡j(mod2n-1).再结合引理1得到两个共轭类中元素都是每两个都相连.且有bai=ai(2n-1-2)b,此即共轭类b={aib}(0≤i≤2n-1),i为偶数.
这样得出,当t=0,r=-1,m=1时,亚循环2-群二阶元分为两个共轭类,且每个共轭类长度都为2n-1,其中的元都是每两个相连,为1-正则图.
2)m≥2.此时b2m=1,(b2m-1)={(b2m-1),(b2m-1)a,(b2m-1)a2,…,(b2m-1)a2n-1-1}.
由ba=a-1b,ab=ba-1得:(b2m-1)ai=a-ib2m-1ai=a-ib2m-1-1a-ib=a-ib2m-1-2aib2=…=a-iaib2m-1=b2m-1.因此共轭类(b2m-1)={b2m-1}就一个二阶元.
考虑所有的二阶元,aibjaibj=aibj-1baibj=aibj-2ba-ibj+1=aibj-2aibj+2,若j为奇数,则aibjaibj=b2j不可能等于1;若j为偶数,aibjaibj=a2ib2j=1⟺i≡0(mod2n-1),j≡0(mod2m-1)(0≤i≤2n-1,0≤j≤2m-1).i,j可各自取2n-1,2m-1即总共3个二阶元.故当t=0,r=-1,m≥2时,亚循环2-群二阶元分为3个共轭类,且每个共轭类长度都为1,都为孤立点图.
情形2t=0,r=1.此时有a2n=1,b2m=1,ab=a.由ab=a⟺ab=ba.存在二阶元共轭类(b2m-1)={b2m-1,(b2m-1)a,…,(b2m-1)a2n-1-1}.由ab=ba可得:(b2m-1)ai=b2m-1,即该共轭类中只有一个二阶元.考虑所有的二阶元,aibjaibj=a2ib2j=1(0≤i≤2n-1,0≤j≤2m-1)⟺i≡0(mod2n-1),j≡0(mod2m-1),故i=2n-1,j=2m-1.总共3个二阶元.当t=0,r=1时,亚循环2-群二阶元分为3个共轭类,且每个共轭类长度都为1,为孤立点图.
情形3t=0,r≠±1.此时有a2n=1,b2m=1,ab=ar,r2m≡1(mod2n).存在二阶元共轭类(b2m-1)={b2m-1,(b2m-1)a,…,(b2m-1)a2n-1-1}.由ab=ar,r2m≡1(mod2n)可得:
a=(ar)b-1=(ab-1)r⟺bab-1=ab-1=(ab-1)r2m=(ab-1)r·r2m-1=ar2m-1⟺ba=ar2m-1b.
1)m=1.二阶元共轭类(b)={b,ba,…,ba2n-1-1}.此时ba=arb,任意bai=a-ibai=ai(r-1)b.设bai=baj(0≤i,j≤2n-1-1),即:a(i-j)(r-1)=1⟺(i-j)(r-1)≡0(mod2n).
根据引理3,若(r-1)≡0(mod2),(r+1)≡0(mod2n-1),由(i-j)(r-1)≡0(mod2n)得,(i-j)≡0(mod2n-1),即共轭类类长为2n-1.设bbai=baib,即bai(r-1)=ai(r-1)b⟺ai(r-1)r-i(r-1)=1⟺i≡0(2n-2).
取i=2n-2时,bbai=baib,故可知(b)中元每两个相连.所有二阶元aibaib=ai(r+1)=1⟺i≡0(mod2)(0≤i≤2n-1).因此可得此类亚循环2-群有2n-1个二阶元,属一个二阶共轭类,且其中每两个元相连,为1-正则图.
若(r-1)≡0(mod2n-1),(r+1)≡0(mod2),则(i-j)≡0(mod2),类长为2.设bbai=baib,⟺i≡0(mod1),即i可任意取,共轭类中两个二阶元相连.同样所有二阶元aibaib=ai(r+1)=1⟺i≡0(mod2n-1)(0≤i≤2n-1).说明此类亚循环2-群有3个二阶元,2个共轭类,一个类长为2,为1-正则图;另一个中心二阶元,为孤立点图.
b2m-1ar2m-1(2m-1)-1=ar2m-1(2m-1)-1b2m-1⟺ar2m-1(2m-1)(r2m-1(2m-1)-1)-r2m-1(2m-1)+1=1⟺a(r2m-1-1)2=1⟺a-2(r2m-1-1)=1此式恒成立,即共轭类中两个二阶元相连.
再考虑此类亚循环2-群所有二阶元aibaib=ai(rj(2m-1)+1)b2j=1.
⟺j≡0(mod2m-1),i(rj(2m-1)+1)≡0(mod2n)(0≤i≤2n-1,0≤j≤2m-1).
j=2m-1,i(r2m-1+1)≡0(mod2n).由(r2m-1+1)≡0(mod2)⟺i≡0(mod2n-1).因此这类亚循环2-群有3个二阶元,一个中心二阶元,为孤立点图;另两个二阶元属同一共轭类,且相连,为1-正则图.
情形4t≠0,r=-1.此时a2n=1,b2m=at,ab=a-1,r2m≡1(mod2n),t(r-1)≡0(mod2n).由t(r-1)≡0(mod2n),r=-1⟺t=2n-1,故有b2m+1=1.存在二阶元共轭类(b2m)={b2m,(b2m)a,…,(b2m)a2n-1-1}.再由ab=a-1⟺ab=ba-1⟺ba=a-1b.共轭类中元(b2m)ai=a-ib2mai=a-ib2m-1bai=a-ib2m-2ba-ib=a-ib2m-2aib2=a-iaib2m=b2m只有一个二阶元.
考虑所有的二阶元,aibjaibj=aibj-1baibj=aibj-2ba-ibj+1=aibj-2aibj+2,若j为奇数,则aibjaibj=b2j不可能等于1;若j为偶数,aibjaibj=a2ib2j=1⟺i≡0(mod2n-1),j≡0(mod2m)(0≤i≤2n-1,0≤j≤2m-1),因此j值只能取0,即总共1个二阶元,此时b2m=a2n-1为中心二阶元,为孤立点图.
情形5t≠0,r=1.此时有a2n=1,b2m=at,ab=a,r2m≡1(mod2n),t(r-1)≡0(mod2n).

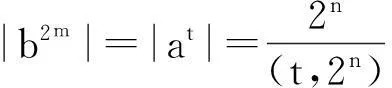
k1>0时,此亚循环2-群群只有一个二阶元,即中心二阶元,为孤立点图;k1=0时,设(bk)ai=(bk)aj,故有ai-j(rk(2m-1)-1)=1⟺i-j(r2m-1(2m-1)-1)≡0(mod2n). 以下分为两种情况讨论.
1)m=1 (i-j)(r-1)≡0(mod2n).若(r-1)≡0(mod2),(r+1)≡0(mod2n-1),由(i-j)(r-1)≡0(mod2n)得:
(i-j)≡0(mod2n-1),即共轭类类长为2n-1.设bbai=baib,即:bai(r-1)=ai(r-1)b⟺ai(r-1)r-i(r-1)=1⟺i≡0(2n-2).
取i=2n-2时,bbai=baib.根据引理1知(b)中元每两个相连.所有二阶元aibaib=ai(r+1)=1⟺i≡0(mod2)(0≤i≤2n-1).因此可得此类亚循环2-群有2n-1个二阶元,一个2阶共轭类,且每两个元相连,为1-正则图.
若(r-1)≡0(mod2n-1),(r+1)≡0(mod2),则(i-j)≡0(mod2),类长为2. 设bbai=baib,⟺i≡0(mod1),即i可任意取,共轭类中两个二阶元相连.同样所有二阶元aibaib=ai(r+1)=1⟺i≡0(mod2n-1)(0≤i≤2n-1).说明此类亚循环2-群有3个二阶元,两个共轭类,一类为中心二阶元,为孤立点;另一个类长为2,它们是相连的,为1-正则图.
2)m≥2.(i-j)(r2m-1-1)≡0(mod2n).(i-j)≡0(mod2),此二阶元共轭类长度为2.同时,若b2m-1(b2m-1)a=(b2m-1)ab2m-1,则b2m-1ar2m-1(2m-1)-1=ar2m-1(2m-1)-1b2m-1⟺a(r2m-1-1)2=1⟺a-2(r2m-1-1)=1此式恒成立,即共轭类中两个二阶元相连.再考虑此类亚循环2-群所有二阶元aibaib=ai(rj(2m-1)+1)b2j=1.⟺j≡0(mod2m-1),i(rj(2m-1)+1)≡0(mod2n)(0≤i≤2n-1,0≤j≤2m-1).j=2m-1,i(r2m-1+1)≡0(mod2n).由(r2m-1+1)≡0(mod2)⟺i≡0(mod2n-1).因此这类亚循环2-群有3个二阶元,一个中心二阶元,故为孤立点图;另两个二阶元属同一共轭类,且相连,故为1-正则图.
情形7 n=1.此时设亚循环2-群为A,|A|=2m+1.由亚循环2-群的定义式知A/{1,a}≅C2m,故有:
A≅Z2x1×Z2x2×…×Z2xk,1≤x1≤x2≤…≤xk,x1+x2+…+xk=m+1⟹A≅C2m+1或者A≅Z2×C2m,而Z2×C2m中有3个二阶元,3个共轭类,故为三个孤立点图;C2m+1中只有一个二阶元,为孤立点图.
参考文献:
[1]RICHARDBrauer,FOWLERKA.Ongroupsofevenorder[J].AnnofMath,1955,62:565-583.
[2]ANDREIS,RAPINCHUK,YOAVSegev,etal.Finitequotientsofthemultiplicativegroupofafinitedimensionaldivisionalgebraaresolvable[J].JAmerMathSoc,2002,15(4):929-978 (electronic).
[3]BERNDFischer.Finitegroupsgeneratedby3-transpositions[M].WarwickMathematicalInstitutePreprint,1970.
[4]BERNDFischer.Finitegroupsgeneratedby3-transpositions[J].IInventMath,1971,13:232-246.
[5]BATESC,BUNDYD,HARTS,etal.Commutinginvolutiongraphsforsporadicsimplegroups[J].JAlgebra,2007,316(2):849-868.
[6]BATESC,BUNDYD,PERKINSS,etal.CommutinginvolutiongraphsforfiniteCoxetergroups[J].JGroupTheory,2003,6(4):461-476.
[7]BATESC,BUNDYD,PERKINSS,etal.Commutinginvolutiongraphsforsymmetricgroups[J].JAlgebra,2003,266(1):133-153.
[8]BATESC,BUNDYD,PERKINSS,etal.Commutinginvolutiongraphsinspeciallineargroups[J].CommAlgebra,2004,32(11):4179-4196.
[9]徐明曜.有限群导引(上)[M].北京:科学出版社,1999.
责任编辑:时凌
On Commuting Involution Graphs of Meta-cyclic 2-groups
TAN Yanqing,SHEN Rulin
(Department of Mathematics,Hubei University for Nationalities,Enshi 445000,China )
Abstract:For a group G and a conjugacy class X of an involution of G,the commuting graph ΓG(X) of G on X,is the graph whose vertex set is X and distinct vertices x and y having an edge if and only if xy=yx. In this paper,we classify the structure of the commuting involution graph of meta-cyclic 2-groups.
Key words:commuting involution graph;k-regular graph;meta-cyclic 2-group
收稿日期:2015-12-18.
基金项目:国家自然科学基金地区基金项目(11201133).
作者简介:谭延庆(1991- ),男,硕士生,主要从事群论的研究.
文章编号:1008-8423(2016)01-0020-04
DOI:10.13501/j.cnki.42-1569/n.2016.03.005
中图分类号:O152
文献标志码:A
