改进惯性权重的简化粒子群优化算法

高　苇，平　环，张成刚，姜静清

(1.内蒙古民族大学 数学学院，内蒙古 通辽028000;2.内蒙古民族大学 计算机与科学学院,内蒙古 通辽 028000)



改进惯性权重的简化粒子群优化算法

高苇1，平环1，张成刚1，姜静清2*

(1.内蒙古民族大学 数学学院，内蒙古 通辽028000;2.内蒙古民族大学 计算机与科学学院,内蒙古 通辽 028000)

摘要：针对传统的粒子群优化算法收敛速度慢、易陷入局部空间极值的缺点，提出一种基于简化粒子群优化算法同时改进惯性权重的新算法.该算法首先去掉速度项，使算法更加简便，然后改进位移项，最后改进惯性权重.对6个经典函数分别采用传统的粒子群优化算法、简化的粒子群优化算法和该改进的算法进行比较，数值实验表明，该改进的粒子群优化算法比其他两个算法的性能好.

关键词：速度项；惯性权重；经典函数

1995年由Kennedy和Eberhart[1]提出的粒子群优化算法(PSO)是一种由对鸟群研究而得到的智能优化算法，粒子群优化算法是通过对大量的鸟群、鱼群、人类社会系统的研究证实了群体中个体之间信息的社会共享，有助于整体进化.PSO提出后，由于过程简单、原理易懂、收敛速度快，很快得到人们的关注.被运用于很多领域，例如图像处理[2]、硬件加速器[3]、工业[4-5]、生物[6]、财务[7]等.

在粒子群优化算法中参数是很重要的，尤其是惯性权重，它能够影响算法的开发能力和探索能力，因此可以通过调节惯性权重的值来决定了粒子先前飞行速度对当前速度的影响程度.当惯性权重较大时，粒子速度也会增大，局部搜索的能力从而减弱，全局搜索的能力从而增强；当惯性权重较小时，粒子速度也会降小，局部搜索的能力从而增强，全局搜索的能力从而减弱.因此恰当的改变惯性权重值可以很好地提高算法的性能.但是随着研究的深入以及现实中的各种问题的出现如数学精确度[8]，逐渐暴露出传统PSO算法的各种问题，主要有粒子易陷入局部空间最优、后期粒子收敛速度过慢、搜索解的精度低等.为了增强粒子群优化算法的性能，人们从很多方面进行了改进.例如文献[9]经过反复实验建议惯性权重采用从0.9线性递减到0.4的策略.文献[10]对粒子群算法更新公式进行简化，即去除掉速度项公式，通过位置公式进行粒子更新.并通过随机分布的方式获取惯性权重从而提高粒子群算法的搜索能力，同时采用异步变化的学习因子的策略来改善粒子的学习能力.文献[11]提出改进的PSO算法不包含速度项参数，利用所有粒子的个体最优位置信息，提高算法的性能.本文在文献[11]的基础上，为了更好的搜索到目标函数值，对惯性权重进行了改进，通过粒子与粒子之间的影响，去掉速度项，同时利用迭代次数对惯性权重进行动态改进，从而增强粒子群优化算法更新公式的收敛能力，并且改进粒子群算法极易陷入局部搜索最优的缺点.

1传统的粒子群优化算法

首先PSO算法初始化产生一群没有体积没有质量的随机粒子，每个粒子都有位移项和速度项，可以把每个粒子当作一个可行解，而真正好的可行解还要用适应度函数来确定.一般情况下在解空间进行搜索粒子都追随所在种群最好的粒子，并不断更新自身的位置，逐代搜索得到所要求的最优解.

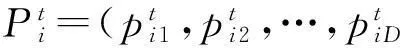
对于每个粒子i的第d维的速度和位置分别按下面公式进行更新.

(1)

(2)

其中：t为当前迭代次数，w为惯性权重，c1，c2为学习因子，r1，r2为[0，1]之间的随机数.

式(1)有三个成面构成：第一个成面是当代粒子对前代粒子速度的继承学习，表现当代粒子对前一代运动过程的认可；第二个成面是当代粒子对粒子自身的识别，表示粒子结合自身以往的经历思考学习的认知；第三个成面是算法对全部粒子的辨识，表示各个粒子间的信息共享与相互合作.这个更新公式必须是合法的，更新完之后检查位置是否合法.若不合法必须进行修正，修正一般是重新随机设定位置或限定在边界，通常在搜索空间PSO算法终止条件是达到设定的迭代次数或者是达到目标函数需要的精确度.

2粒子群优化算法的改进

1)去掉速度项.为了避免传统粒子群优化算法容易陷入局部极值，进化后期的收敛速度慢和精度低等问题，文献[11]对传统的粒子群算法更新公式进行了改进，即去掉速度更新公式，在搜索过程仅由位置更行公式进行迭代，从而得到更加简单的结构的粒子群优化算法.在传统PSO算法搜索过程中，粒子根据速度项来变换位移项，并没有考虑粒子与粒子之间的影响.事实上，粒子之间是有影响的.通过去掉粒子速度项，迭代方程也由原来的两个更新公式降为一个公式，同时利用了粒子最优位置，得到简化粒子群优化算法.更新公式如下：

(3)

其中：pad为所有的个体最优位置的平均值，pid为粒子自身个体最优位置，pgd为粒子种群的全局最优位置.这个方法使得粒子在迭代过程更简便，比传统的粒子群算法更快的得到最优解.

2)改进惯性权重.在去掉速度项的简化粒子群优化算法的基础上，再对传统PSO算法中的惯性权重进行改进.在PSO算法中惯性权重很重要，通过改进惯性权重能够有效地提高PSO算法的搜索性能.一般固定情况下把w设为0.729对算法更有利[12]，非固定的有非线性的情况[13-14]和线性的情况[15]等.

传统的PSO算法一般采用线性减少的惯性权重，但是随着搜索空间的范围逐渐缩小，使得粒子容易收敛到局部邻域的极值点，从而使得粒子群算法极易收敛到局部极值.

为了解决上述PSO算法的不足，本文在动态改变惯性权重的粒子群优化算法基础上，对惯性权重更进一步改进.改进的惯性权重如下：

(4)

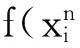
前半部分e-αn/αn-1中，根据所得函数值αn指标在每次迭代时都进行变化.通过位置的改变使得w线性减小，从而使wn动态改变.在式(4)中惯性权重wn充分利用了目标函数的信息，增强了搜索方向的启发性.又因为αn较大，αn/αn-1在不同的迭代次数中变化也过大，因此式(4)以e为底来降低它们的变化幅值，改善wn的平滑性，从而使得e-αn/αn-1在[0，1]内，但是还存在着一定的收敛速度过快和陷入局部极值的缺点.为了更接近基本PSO算法w的取值区间[0.4，0.9]，在后面添加了一个线性递增的公式(wini-wfin)tn/tmax，此公式随着每次迭代次数的增加而变化.用前半部分减去后半部分，使得整个惯性权重在动态递减，而且更加接近[0.4，0.9].当0<αn/αn-1<1时，说明在这次迭代中算法总体呈现收敛，当αn/αn-1数值减小，wn将越来越接近0.9，迭代之间的步长增大；当αn/αn-1>1时说明在这次迭代中算法总体呈现发散，αn/αn-1比值增大，wn将慢慢接近0.4，迭代之间步长减小.

在式(4)中前半部分不仅单调减小，而且与目标函数紧密联系，同时通过后半部分的调节，使惯性权重起伏不至于过大.这使得粒子群优化算法改进后不仅加快了收敛的速度，而且局部最优问题得到很好的解决.

3改进后的PSO算法的步骤

2)根据式(4)计算出惯性权重；

3)计算各个粒子的函数适应度值，并进行判断最优适应度值；

4)根据式(3)对粒子的位置进行更新；

5)若粒子群迭代达到搜索的终止条件，就输出目标函数的极值，若不然回到步骤3)再次根据步骤搜索.

4 函数测试

为了验证改进后PSO的效率，采用6个常用的目标函数对其进行测试，并对仿真结果的数据与标准的粒子群优化算法[1]、简化粒子群优化算法进行对比.所需的参数设置如下：粒子种群规模m=30，维数D=20，最大迭代次数50，学习因子c1=c2=2.05.

6个基准测试函数[16-18]如下：

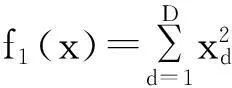
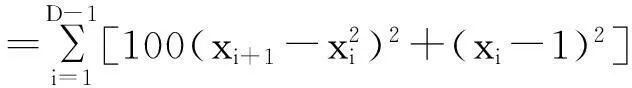
表1～3显示对于Sphere函数，采用三种算法，分别迭代50次的适应度值变化情况,结果见表1～3.

图1和图2是Rosenbrock和Shaffer′sf 6在三种粒子群优化算法下性能的比较.分别采用三种算法各自计算50次，图中所用数据是最好一次的适应度值.从图1中可以看出简化后的PSO算法和本文提出的改进PSO算法比标准的PSO算法收敛速度快，可以快速搜索到目标函数的准最优解.但是这两个图不能明显的看出简化的PSO算法和本文的改进PSO算法的性能差异，所以又单独对两种方法进行比较.图3和图4是Rosenbrock和Shaffer′sf 6函数采用这两种方法的性能比较.从这两个图可以明显地看出本文改进的PSO算法的性能优于简化的PSO算法的性能.改进的惯性权重使得搜索前半部分位移变化速度快，后半部分位移变化速度慢，防止陷入局部最优，能够更好的搜索目标函数的值.

表1　传统粒子群算法下的适应度值的变化

表2　简化粒子群算法下的适应度值的变化

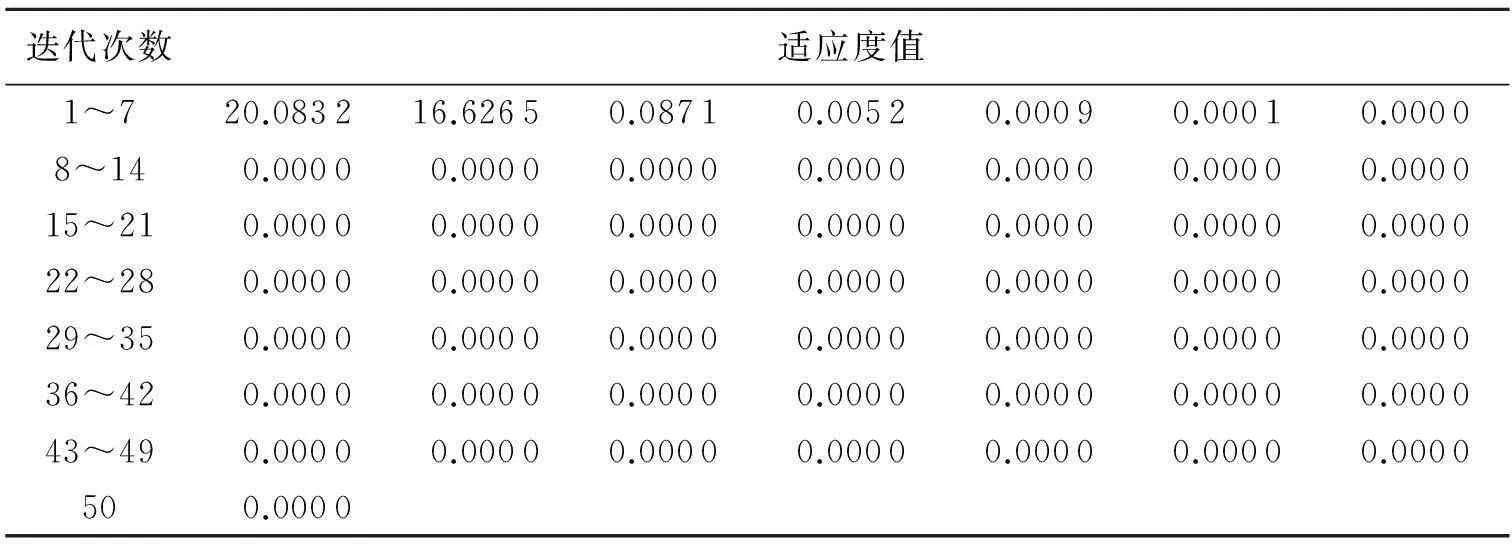
表3　本文改进的算法下的适应度值的变化

图5～7分别表现了三种算法对6个函数计算时适应度值的变化.

5结论

针对传统的粒子群优化算法速度收敛较慢而且易陷入局部空间极值的缺点，本文提出一种对惯性权重进行改进的PSO算法.该算法首先去掉速度项，使算法更加简便，然后利用例子之间的关系和迭代次数改进位移项.最后改进惯性权重，使算法在开始时权重变化较大，后期权重变化较小，有利于局部搜索.对6个经典函数分别采用传统的粒子群优化算法、简化的粒子群优化算法和本文改进的算法进行比较，实验结果表明，本文改进的粒子群优化算法的收敛速度快，同时避免了陷入局部极值，该算法性能优于其他两个算法.

参考文献:

[1]J Kennedy，R C Eberhart.Particle swarm optimization[J].Proc IEEE Int Conf Neural Networks，1995(4)：1942-1948.

图1　Rosenbrock函数在三种算法中适应度值的变化 图2　Shaffer′s f 7函数在三种算法中适应度值的变化

图3　Rosenbrock函数在两种算法中适应度值的变化 图4　Shaffer′s f 7 函数在两种算法中适应度值的变化

图5　基本PSO算法中6个函数的适应度值变化 图6　简化的PSO算法中、6个函数的适应度值变化

图7　本文改进的PSO算法中6个函数的适应度值变化Fig.7　The fitness of the improved PSO algorithm in six fitness function value changes

[2]SETAYESHh M，ZHANG Mengjie，JOHNSTON M.A novel particle swarm optimization approach to detecting continuous,thin and smooth edges in noisy images[J].Information Sciences，2013，246：28-51.

[3]CALAZAN R M，NEDJAH N，MOURELLE L M.A hardware accelerator for particle swarm optimization[J].Applied Soft Computing，2014，14：347-356.

[4]ECHEVARR L C，SANTIAGO O L，FAJARDO J A H,et al.A variant of the particle swarm optimization for the improvement of fault diagnosis in industrial systems via faults estimation[J].Engineering Applications of Artificial Intelligence，2014，212：1-16.

[5]孙志民，赵珺，王伟.基于高斯搜索的改进粒子群优化在磨矿预测控制中应用[J].大连理工大学学报，2015，55(1):89-96.

[6]李娜，黄治国.改进的小生物粒子群优化算法[J].软件导刊，2015，14(2):45-47.

[7]彭静，彭勇，欧阳令南.基于粒子群算法和支持向量机的财务危机预警模式[J].上海交通大学学报，2008，42(4):615-620.

[8]华志强，张春生.长尾加权相依的随机变量和的精度大偏差[J].湖北民族学院学报(自然科学版)，2015，33(2)：121-123.

[9]SHI Y，EBERHART R C.Fuzzy Adaptive Particle Swarm Optimization [C]// Proceedings of the Congress on Evolutionary Computation,Seoul,Korea,2001：101-106.

[10]赵志刚，黄树运，王伟倩. 基于随机惯性权重的简化粒子群优化算法[J].计算机应用研究，2014，31(22)：361-363.

[11]胡旺，李志蜀.一种更简化而高效的粒子群优化算法[J].软件学报，2007，18(4)：861-868.

[12]SHI Y，EBERHART R C.Empirical Study of Particle Swarm Optimization[C]// Proc IEEE Congr Evol Comput，1999：1945-1950.

[13]邵洪涛，秦亮曦.带变异算子的非线性惯性权重PSO算法[J].计算机技术与发展，2012，22(8)：30-38.

[14]CHATTERJEE A，SIARRY P.Nonlinear Inertia Weight Variation for Dynamic Adaption in Particle Swarm Optimization [J].Comput Oper Res，2006，33：859-871.

[15]YANG Tang，WANG Zidong，FANG Jianan.Feedback learning Particle Swarm Optimization[J].Appl Soft Comput，2011，11：4713-4725.

[16]纪震，廖惠连，吴青华.粒子群算法及应用[M].北京：科学出版社，2009：87-98.

[17]刘金承,费佳慧.改进的动物迁徒算法求解全局优化问题[J].长春大学学报,2015,25(8)：42-49.

[18]谷志刚,孙锋利.基于粒子群脊波神经网络的飞机目标识别[J].延边大学学报(自然科学版),2014,40(4)：346-351.

责任编辑：时凌

Simplified Particle Swarm Optimization Algorithm Based on Improved Inertia Weight

GAO Wei1，PING Huan1，ZHANG Chenggang1，JIANG Jingqing2*

1.College of Mathematics，Inner Mongolia University for the Nationalities，Tongliao 028000，China；2.College of Computer Science and Technology,Inner Mongolia University for the Nationalities，Tongliao 028000，China)

Abstract：For the shortcomings of the traditional particle swarm optimization algorithm,which is easy to fall into local extreme,a new algorithm based on the simplified particle swarm optimization algorithm is proposed.Firstly，it removes the speed term，so it makes the algorithm simple.And then it mproves the displacement term.Finally it improves the inertia weight.Six classical functions are used to compare the traditional particle swarm optimization algorithm,the simplified particle swarm optimization algorithm and the improved algorithm proposed in this paper.The experimental results show that the performance of the improved particle swarm optimization is better than the other two algorithms.

Key words：velocity term；inertia weight；classical functions

收稿日期：2015-11-16.

基金项目：国家自然科学基金项目(61373067，61163034)；内蒙古自然科学基金项目(2013MS0910).

作者简介：高苇(1991- )，女，硕士生，主要从事智能算法的研究；*通信作者：姜静清(1968- )，女，博士，教授，主要从事计算智能、楼式识别、深度学习的研究.

文章编号：1008-8423(2016)01-0011-05

DOI:10.13501/j.cnki.42-1569/n.2016.03.003

中图分类号：O224

文献标志码：A