城市快速路匝道及变速车道控制参数研究

莫　阳

(悉地(苏州)勘察设计顾问有限公司, 江苏　苏州　215123)



城市快速路匝道及变速车道控制参数研究

莫阳

(悉地(苏州)勘察设计顾问有限公司, 江苏苏州215123)

摘要：从分析出入口特性出发，寻找了确定匝道及变速车道控制参数的影响因素，解析了匝道设计速度和停车视距对匝道曲线最小半径、交通流率和匝道设计速度对变速车道长度和渐变段长度的影响机理。基于运动学原理、交通流理论、概率论等知识，建立了匝道及变速车道控制参数的计算模型。分析和计算结果表明：匝道设计速度宜按照匝道形式及两端连接道路的性质分级确定；对结构物形式匝道，满足停车视距要求的曲线最小半径比满足横向力系数要求的大；对双车道加速车道和宽度渐变段，在考虑交通流率影响状况下的长度计算值均比现行规范的要求值大。

关键词：交通工程；控制参数；计算模型；匝道；变速车道；横净距；车头时距

0引言

城市快速路(网)的运行状态，除了受规模容量限制外，出入口是最重要的影响因素，往往成为拥堵易发生点。朱胜跃[1]研究了快速路出入口类型、间距及设计需考虑的问题，指出要用60%的时间做好出入口设计；詹琳霞[2]归纳了影响快速路出入口设置的4类因素，采用DEA/AHP两阶段集成模型，对出入口组合形式、交通组织方式、主辅路流量比及地面交叉口距离的影响进行了仿真；汪洋[3]分析了快速路出入口与公交站点的相互影响，提出了出入口附近设置公交站点的一般性准则；杨晓光等[4]从交通运行的角度出发，提出快速路上公交停靠站与出入口最小间距的计算方法。以上研究成果均对城市快速路出入口设计提供了很好的参考，但以往研究主要关注出入口的组合、间距，对出入口特性、匝道和变速车道特性、以及交通流对匝道和变速车道影响的分析较少。匝道和变速车道的技术参数取决于出入口特性，其合理与否直接影响出入口功能的实现，若处理不当将降低交通转换效率，进而引起主路运行状态的紊乱。

本文基于快速路出入口特性，从功能角度提出新的出入口分类方法，分析出入口及匝道的特性对匝道的影响和主路交通流对变速车道技术参数的影响，由匝道和变速车道特性要求导出相关的控制参数。

1出入口及匝道特性

城市快速路由快速道路和一般道路两个系统组成，对应存在两种衔接关系：一是快速道路系统之间的衔接，二是快速道路系统与一般道路系统之间的衔接。城市快速路出入口是供车辆驶出或进入快速路的单向交通入口，设置于快速路右侧，一般通过互通式立交匝道、高架路匝道或辅路匝道连接[5]。

城市快速路的出入口可分为两大类：连接快速道路系统之间的出入口称为快-快转换出入口；连接快速道路系统与一般道路系统的出入口称为快-慢转换出入口。出入口的特性归纳于表1中。

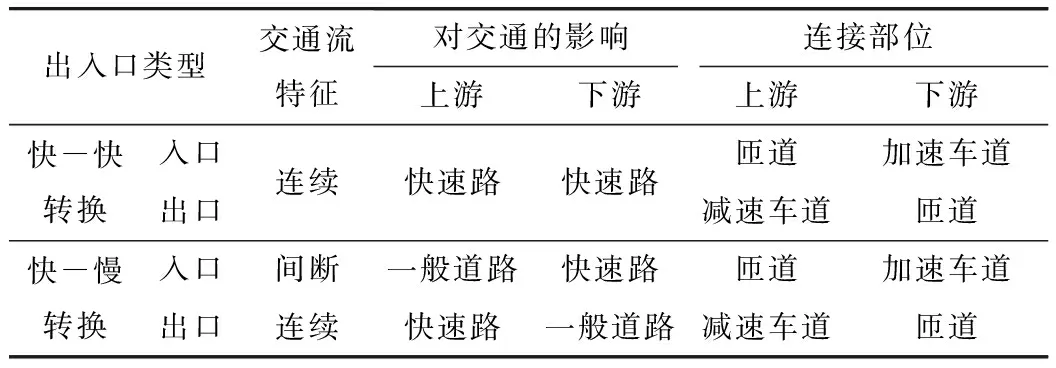
表1　城市快速路出入口特性

不同类型的出入口或其组合，决定连接其匝道的性质、适宜的型式及适宜的行驶速度，见表2。

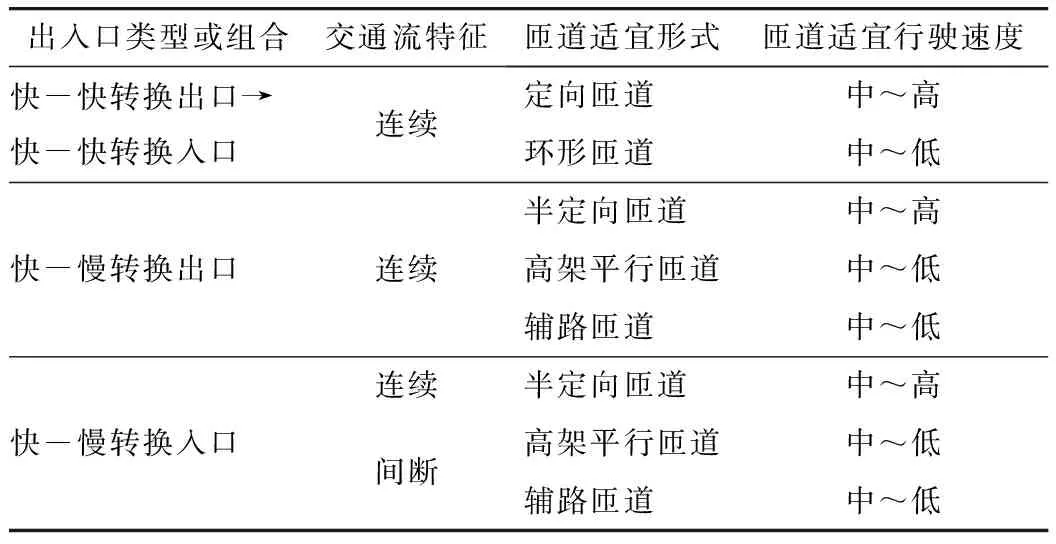
表2　匝道特性与出入口类型或组合的关系

2匝道控制参数

匝道设计速度既要保证线形受限制路段的行驶安全[6-7]，又要考虑分、合流时与主路的行驶速度协调。城市道路规范[8-9]仅规定匝道与主路间设计速度的关系，实践中在选择性增大的同时，也带来选择依据不明的新问题，而设计速度决定其他参数，按照匝道的性质和形式来确定恰当的设计速度是必要的。

以往对曲线匝道最小半径的分析主要从车辆动力性能出发，考虑弯道行驶的舒适和安全[10]，车队情形下前、后车间的安全要求则通过验算停车视距予以保证。城市快速路匝道的构筑形式分为路基式和结构物式两种。路基式匝道可采用清除视距包络线范围内影响视线的障碍物来满足平曲线视距要求[9-10]。结构物式匝道又分为隧道式和桥梁式两种。隧道式匝道两侧均被土体遮挡。桥梁式匝道两侧一般设置混凝土护栏以防止车辆越出[5]，根据试验，大型车碰撞的接触点距路面70 cm，防撞墙高度一般采用80 cm[10]，小型车尾灯距路面高度基本不超过此数值。当夜间行驶于半径过小的结构物形式曲线匝道时，后车看不到前车尾灯，则存在来不及反应的安全隐患。对于结构物形式的曲线匝道，验算按横向稳定性要求获得的最小半径是否能满足停车视距就十分必要。

2.1匝道设计速度

根据出入口特性，快-快转换匝道实现顺畅的交通转换，要求较高的行驶速度，宜选取较高的设计速度；快-慢转换匝道与一般道路连接，行驶速度受一般道路制约，宜选取较低的设计速度。匝道及集散车道设计速度宜为主路的0.4～0.7倍[8-9]，据此匝道设计速度为24～70 km/h，覆盖低速至中高速的跨度范围。不同交通特性的匝道采用跨度范围内的任意速度显然不合理，需要对匝道设计速度选择范围进行合理划分。一般道路最高设计速度为60 km/h[8-9]，快-慢转换匝道往往结合平面交叉口设置，交叉口内的设计速度宜为路段的0.5～0.7倍[8]，则最高为42 km/h，故以40 km/h为临界速度将匝道设计速度划分成高、低两个分区较适宜。

匝道设计速度的高值由快速路主路及匝道的运行速度决定。主路设计速度为60～100 km/h时，稳定流状态的最小平均速度为44～62 km/h[8]，匝道端部的行驶速度为40～55 km/h[10]，汇入主路的最小合流速度为60～65 km/h[10]。考虑主路与匝道运行速度的匹配性，采用60 km/h较适宜。

匝道设计速度的低值由快速路主路与匝道间转换、匝道与一般道路衔接所需的速度决定。快-慢转换匝道通常与主、次干路在平交口附近衔接，该部位的速度宜为20～40 km/h[8]。快速路主路设计速度为60～100 km/h时，加速所需的起始最小速度和安全运行可减到的最小速度为30 km/h[10]。考虑匝道与一般道路运行速度的匹配性，采用30 km/h较适宜。

匝道形式对设计速度的影响为：环形匝道受线形条件制约，可达到的行驶速度较低，宜选取低分区范围的设计速度；其他形式匝道线形条件相对较好，宜选取高分区范围的设计速度。

按以上分析并考虑与主路设计速度的匹配，匝道适宜的设计速度推荐如下。

表3　匝道设计速度的推荐值(单位：km/h)

2.2结构物型式匝道最小半径的检验

结构物型式匝道按设计速度确定最小半径后要满足停车视距的要求，则最大横净距宽度内视线不能被遮挡；圆曲线长度大于停车视距时的横净距在所有平曲线组合方式中为最大，则最大横净距a可表示为：

(1)

式中，S为停车视据；R为车辆行驶轨迹的半径。

以往对车辆行驶轨迹半径规定为未加宽前路面内边缘半径加1.5 m[10]，计算时需要先确定路面内边缘半径，而此半径并非平曲线的半径，容易混淆概念且不便于应用。车辆行驶时有占居车道中央的趋向，以未加宽前的车道中心线半径作为车辆行驶轨迹半径的概念较清晰同时便于应用，故以下讨论中的匝道最小半径均指未加宽车道的中心线半径。

(1)单车道匝道

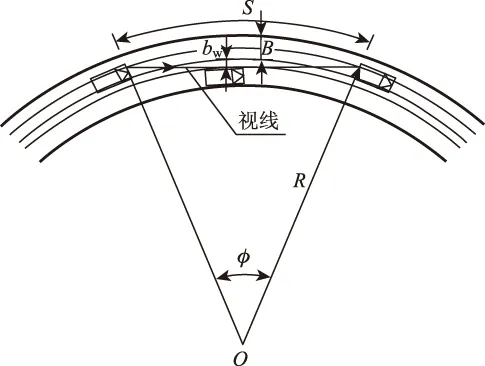
图1　单车道结构物形式匝道的最小半径与停车视距的关系Fig.1　Relationship between minimum curve radius of single-lane structural ramp and stopping sight distance

图1为单车道结构物型式曲线匝道，R为未加宽车道中心线最小半径；S为停车视距；B为未加宽车道宽度；bw为车道加宽值。

最不利情形为紧急停车带有车辆停靠，此时最大横净距a不能大于未加宽车道宽度B的一半与车道加宽值bw之和，即应满足：

(2)

式(2)取等号时车道中心线的半径最小，将车道加宽值bw的表达式[9]代入式(2)并整理后可得：

(3)

式中，V为匝道设计速度；agc为小型车、大型车轴距加前悬的长度；acr为铰接车后轴距的长度；其余符号意义和单位同前。

根据行车舒适和安全所需的最小半径[10]及规定的停车视距[9]，可知(S/2R)<1，式(3)左端按幂级数展开并略去四次方及以上项，化简整理后可得：

(4)

由式(4)可解得单车道结构物型式匝道的最小半径R为：

(5)

(2)双车道匝道

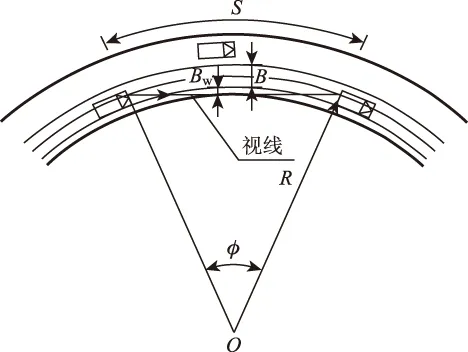
图2　双车道结构物形式匝道的最小半径与停车视距关系Fig.2　Relationship between minimum curve radius of two-lane structural ramp and stopping sight distance

图2为双车道结构物型式曲线匝道，R为内侧未加宽车道中心线最小半径；S为停车视距；B为未加宽车道宽度；bw为车道加宽值。

最不利情形出现在曲线内侧车道，此时内侧车道的最大横净距a，仍需满足式(2)所表述的条件，故双车道结构物型式匝道的最小半径R仍可用式(5)来表示。

按照上述分析，匝道的圆曲线半径以车道中心线半径来度量，单车道匝道为行车道中心线半径，双车道匝道为内侧车道中心线半径。利用式(5)计算的最小半径列于表4，设计速度V取表3所列范围内数值，车道宽度B取3.5 m[8]，大型车和小型车的停车视距S采用一般规定值，铰接车采用货车规定值[9]。

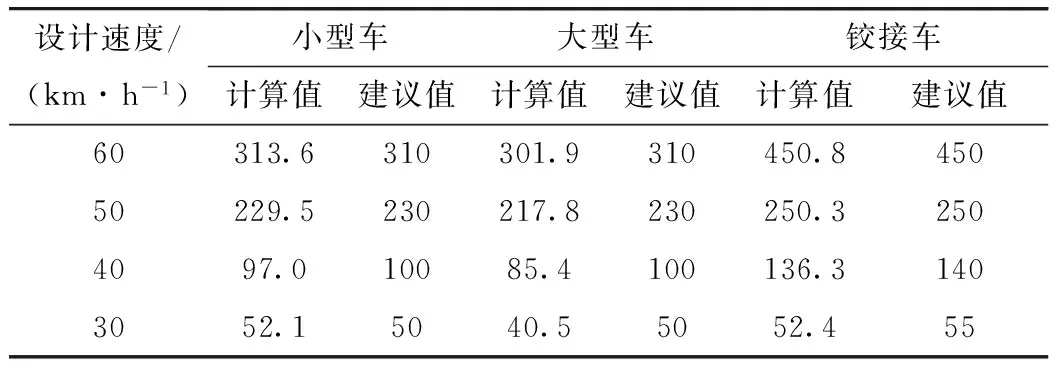
表4　满足停车视距要求的结构物形式匝道最小半径的

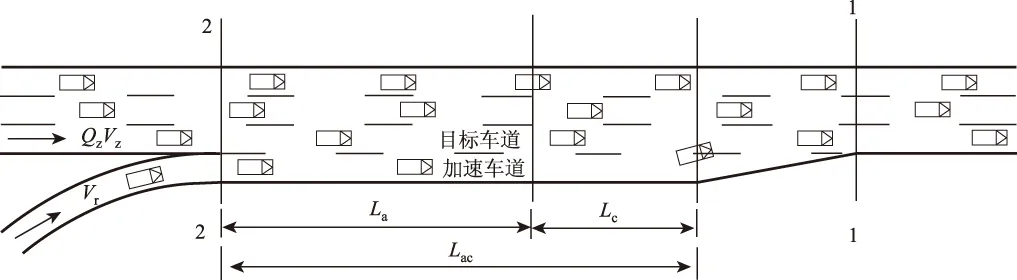
图3　单车道加速车道最小长度组成Fig.3　Minimum composed length of single-lane acceleration lane

大型车的计算值比小型车的略小，是由于车道加宽值较大引起的。与采用横向力系数计算的匝道最小半径[10]相比，各设计速度下均有增大，以设2%超高最小半径为例，40 km/h及以下增幅为25%～50%，40 km/h以上增幅超100%。因此当采用结构物形式匝道且视线易被遮挡时，匝道圆曲线最小半径应按停车视距的要求进行检验，建议条件允许时按横向力系数和停车视距的要求进行双控。

3变速车道控制参数

以往对变速车道长度的分析，主要从车辆动力性能出发，考虑分、汇流的安全，而未考虑交通量的影响。前车从主路分流到减速车道，相当于增大了后车的安全距离，故对减速车道长度，可只考虑分流车辆减到匝道设计速度所需要的安全距离。加速车道中的车辆汇入主路，相当于减小主路中后车的安全距离，故对加速车道长度，除受最小合流速度影响外，还受主路可插入空隙的影响。

以往对变速车道宽度渐变段的分析，仅考虑了单车道变速车道的情形[10]，对双车道变速车道的情形，若直接采用单车道的分析结论，既不能解释指标的由来也不尽合理，有必要作进一步分析。

3.1加速车道最小长度组成

考虑交通量影响，此时的最不利情形为：车辆在达到与主线合流需要速度[10]前不能汇入目标车道，达到合流速度后需找到穿插间隙才能汇入目标车道，则加速车道最小长度应满足：

(6)

式中,Lac为加速车道最小长度；La为汇入车辆驶出匝道后加速到合流所需速度的行驶长度；Lc为汇入车辆找到穿插间隙前的平均行驶长度。

La可按文献[5]及[10]进行计算，Lc按下述方法计算。

(1)单车道加速车道

图3中，单车道匝道设计速度为Vr，目标车道流量为Qz，车速为Vz，当目标车道的车头时距大于临界车头时距τ时，车辆才可汇入。

设目标车道的车头时距t服从指数分布，则密度函数：

(7)

小于临界车头时距τ的车头时距平均值hτ为：

(8)

在加速到合流所需速度Vc的过程中，若目标车道相邻两车车头时距足够，车辆可在La范围内某一位置开始汇入，最不利情形为行驶La后才有机会，在Lc范围内某一位置开始汇入时，找到穿插间隙前的最大等待时间为τ，平均等待时间为hτ，则车辆汇入目标车道需要行驶的平均长度Lc为：

(9)

(10)

将式(7)代入式(10)并引入负荷度Sr=Qz/C，其中C为目标车道的通行能力，可得单车道加速车道的Lc为：

(11)

(2)双车道加速车道

图4中，双车道匝道设计速度为Vr，目标车道流量为Qz，车速为Vz，外侧加速车道上车辆汇入目标车道，第1步移入内侧加速车道，第2步汇入目标车道。此时加速车道最小长度为：

(12)

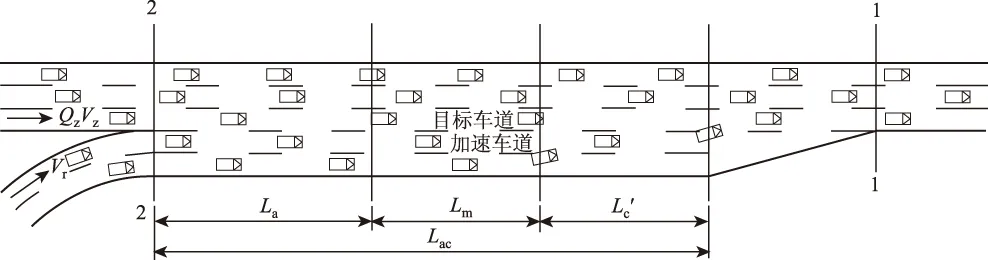
图4　双车道加速车道最小长度组成Fig.4　Minimum composed length of two-lane acceleration lane

为了便于汇入目标车道，汇入车辆会向内侧加速车道汇集，在此过程中出现的最不利情形是：外侧加速车道车辆达到合流需要速度后，才有机会移入内侧加速车道。此时移入内侧加速车道的最小长度Lm为:

(13)

式中，Lm为汇入车辆在最不利情形下移入内侧加速车道的最小长度；Vc为合流所需速度，τ′为车辆移入内侧加速车道的临界车头时距；tm为车辆横移一条车道所需时间。

(14)

利用式(11)和式(14)计算Lc需要的参数中，tm及Vc分别按文献[2]及[10]确定，其他参数的计算方法由下面各节给出。

3.2临界车头时距

车辆汇入目标车道时的临界车头时距τ应满足：

(15)

式中，tf为汇入车辆与目标车道前车间的安全时距；tb为汇入车辆与目标车道后车间的安全时距；tv=Lv/Vz为目标车道后车以速度Vz行驶过汇入车辆车身长度所需的时间，其中Lv为汇入车辆车身长度；ts=Ls/Vz为以速度Vz行驶过汇入车辆停止后与前、后车最小安全距离所需的时间，其中Ls为车辆停止后与前、后车的最小安全距离。

汇入车辆与目标车道的前车安全时距tf和后车安全时距tb，同车辆汇入目标车道的位置有关，以单车道加速车道为例分析如下。

(1)当Vc>Vz时

图5为Vc>Vz情形下车辆汇入目标车道的位置示意。此时，汇入车辆与目标车道前车的安全时距tf为:

(16)

式中，td=|Vz2-Vc2|/(2adVz)为目标车道后车行驶过汇入车辆减速至Vz经过的距离所需时间；ad为汇入车辆减速度；tr为汇入车辆对目标车道前车制动的反应时间。

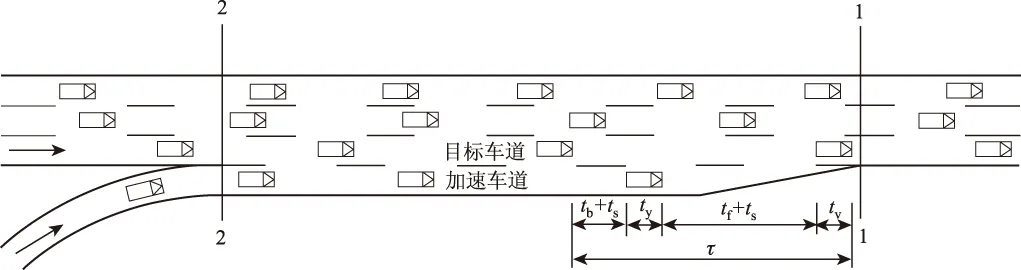
图5　Vc>Vz时车辆汇入目标车道的位置Fig.5　Location of vehicle merging into target lane if Vc>Vz

汇入车辆与目标车道后车的安全时距tb等于目标车道后车对汇入车辆制动的反应时间tr。

(2)当Vc≤Vz时

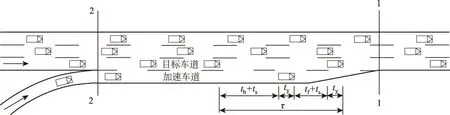
图6　Vc≤Vz时车辆汇入目标车道的位置Fig.6　Location of vehicle merging into target lane if Vc≤Vz

图6为Vc≤Vz情形下车辆汇入目标车道的位置示意。此时，汇入车辆与目标车道后车的安全时距tf等于目标车道后车对汇入车辆制动的反应时间tr。

汇入车辆与目标车道后车的安全时距tb为:

(17)

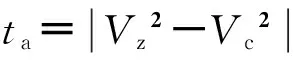
联立式(15)～(17)可解得：

(18)

车辆移入内侧加速车道时的临界车头时距τ′计算方法同上，由于加速车道上车辆加速整体较为均衡，可认为移入过程中没有速度差，由此得τ′为：

(19)

利用式(18)和式(19)计算τ和τ′需要的参数中，Vz的计算方法由下节推导，其他参数可按相关文献确定。

3.3目标车道车速

目标车道车速Vz与流量Qz相关，车辆汇入主要在目标车道完成，目标车道的内侧车道受干扰小，在加速车道长度范围内，主路车辆会向内侧车道汇集以获得平稳的行驶车速和驾驶自由度，当内侧车道流量增加到接近通行能力时，车辆才不得不占用目标车道。

根据理论研究，交通流的速度与流量间的关系存在规律，可用多种模型作定量表述，理论模型各有特点并适用于不同交通流状态。实际交通流有确定的畅行速度、最佳速度及阻塞密度。Greenberg模型适合阻塞流且不存在畅行速度，Underwood模型适合自由流但阻塞密度为无穷大，Edie模型采用分段组合函数避免了上述缺点，但最佳速度与实际调查相差很大。以下讨论限定自由流范围，故设目标车道的速度与流量服从Greenshields模型[11]，即：

(20)

式中，Vf为畅行速度；Kj为阻塞密度。

由Greenshields模型确定的目标车道通行能力C为：

(21)

联立式(20)、(21)消去Vf并引入负荷度Sr=Qz/C，整理后得：

(22)

由式(22)可解得目标车道自由流状态下的车速Vz为：

(23)

利用式(23)计算Vz需要的参数中，C可按文献[8]确定，下面给出阻塞密度Kj的推算方法。

3.4阻塞密度

根据定义，阻塞密度是指车辆停止状态下单位长度内的最大车辆数，其数值通常在115～155 veh/km范围内，实际路段上交通流很少到这种状态[11]。交通流开始出现阻塞与完全阻塞的情形有所不同，从开始阻塞到完全阻塞的过程中，车辆间距逐渐缩小，完全阻塞为静止状态，不具有通常意义上的交通流，故此处阻塞密度表达的含义为：车辆能以很低的均衡速度行驶，前后相邻车辆间无法插入其他车辆，受微小扰动即会导致车队停止行进时的密度。基于以上分析，采用开始阻塞时的交通流密度对阻塞密度进行度量。阻塞密度Kj可表示为：

(24)

式中，Lv为车身长度；Lg为阻塞密度下相邻车辆的平均间距。

交通流开始出现阻塞时的临界密度受行驶速度影响。车辆从较高行驶速度开始减速，至阻塞密度的行驶速度时，车辆平均间距与1个车身长度相当，此时可取Lg=Lv=6 m[8]，则按式(24)算得阻塞密度Kj的最小值为83 veh/km。车辆从较低的行驶速度开始减速，至阻塞密度的行驶速度时，车辆平均间距会小于1个车身长度，但仍需满足安全要求，此时可按停车视距中对安全距离的规定[8]取Lg=5 m，则按式(24)算得阻塞密度Kj的最大值为91 veh/km。

考虑初始车速的影响，计算开始出现阻塞的车流密度值时，设计速度高时阻塞密度取最小值，设计速度低时阻塞密度取最大值，设计速度居中时阻塞密度按线性内插取中间值。

3.5平均行驶长度Lc的计算

按相关文献分别取tm=3.75 s[2]，Lv=6 m[8]，aa=0.36 m/s2，ad=2.4 m/s2[10]，Ls=2 m[11]，tr=1.0 s[11-12]；代入式(11)、式(14)、式(18)及式(19)后得：

(25)

(27)

负荷度Sr=0时，表示目标车道上无车辆行驶的情形，此时车辆汇入没有车头时距限制，故式(25)应用时要求Sr>0。

将阻塞密度Kj的计算值代入式(23)后得：

(28)

上式表明，自由流范围内目标车道的车速仅与目标车道的通行能力及负荷度相关。通行能力C及合流所需速度Vc见表5。

表5　目标车道通行能力及合流所需速度

以目标车道负荷度Sr为变量，按式(25)～(28)计算得到匝道车辆等待汇入目标车道的平均行驶长度，列于表6。

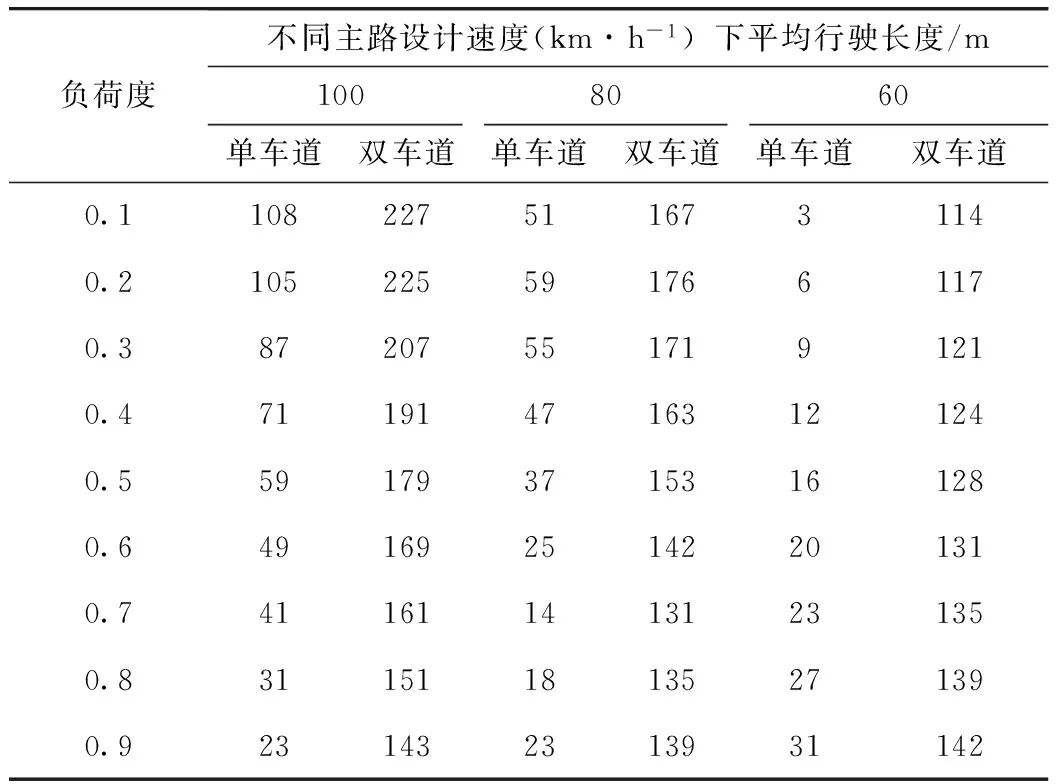
表6　车辆找到穿插间隙汇入目标车道前平均行驶长度计算值

平均行驶长度Lc随负荷度增大的变化规律：设计速度高时呈减小趋势，设计速度低时呈增大趋势，设计速度中等时先减小后增大并出现拐点。

3.6加速车道最小长度讨论

目标车道平均车头时距ha为：

(29)

将式(7)代入并以通行能力C及负荷度Sr表示流量Qz，可得：

(30)

目标车道的临界车头时距τ和平均车头时距ha计算结果如下。

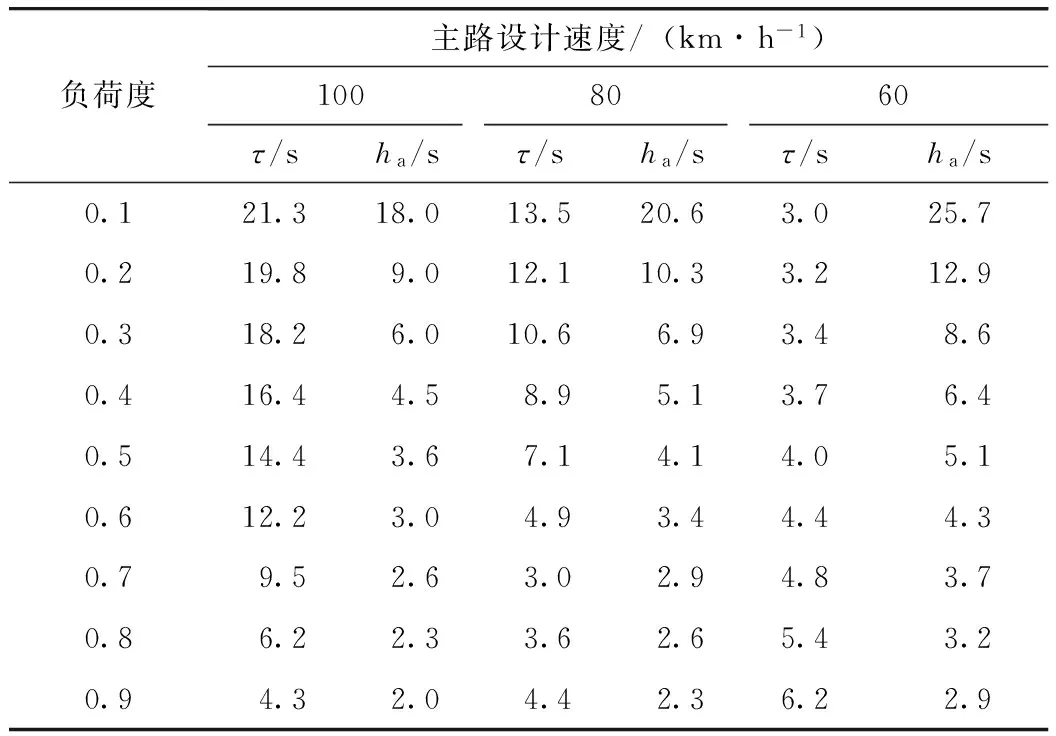
表7　目标车道临界车头时距和平均车头时距计算值

当目标车道负荷度较小时，平均车头时距较大，接近甚至超过临界车头时距，表明车辆汇入目标车道的机会很多，由于车辆经过合流区域有向内侧车道聚拢或减速的倾向，此情形下平均行驶长度Lc即使小于计算值，也可以满足实际需要。随着目标车道负荷度增大，平均车头时距减小，临界车头时距变化与汇入方式相关，加速汇入时随负荷度增大而减小，减速汇入时随负荷度增大而增大；当目标车道负荷度较大时，平均车头时距较小，表明车辆汇入目标车道的机会很少，此情形下平均行驶长度Lc采用计算值，也可能无法满足实际需要。

从设施使用效率的角度看，完全自由流及饱和流状态并非控制重点，稳定流状态则期望能得到有效保持，故以完全自由至稳定流态的目标车道分界点负荷度控制，将该负荷度下Lc的计算值作为平均行驶长度的控制值，具体见下表。

表8　车辆找到穿插间隙汇入目标车道前平均行驶长度的建议控制值

将La及Lc的控制值代入式(6)，得到加速车道最小长度的控制值(不含渐变段)列于表9。

表9　加速车道最小长度的建议控制值

与文献[5]比较，匝道设计速度为40～50 km/h 时，单车道加速车道长度的控制值略大，双车道加速车道长度的控制值明显增大，因而在考虑主路流量影响的情形下，加速车道最小长度的控制值一般比规范取值要大。

表9数据还表明，匝道设计速度对加速车道长度的影响显著，过长的加速车道长度会对驾驶员造成误导而存在安全隐患，因此并不可取。匝道设计速度的选用应充分考虑与主路设计速度的匹配，防止出现较高的主路设计速度与较低的匝道设计速度相组合，避免加速车道长度出现不必要的延长。

3.7宽度渐变段最小长度讨论

变速车道的宽度渐变段也称为宽度缓和段，为考虑车辆变道所需的安全行驶长度所设。AASHO的计算方法[10]为：

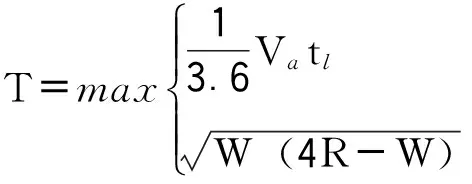
(31)

式中，T为宽度渐变段长度；Va为平均行驶速度；tl为横移变速车道宽度的时间；W为车辆横移宽度；R=Va2/[127(i+f)]为反向曲线半径，i为超高，f为横向力系数。

Va，i，f采用文献[10]推荐数值；W为车道加标线总宽，单车道为4.0m，双车道为7.5 m；tl按横移速率1 m/s[2]计算。计算结果见表10。

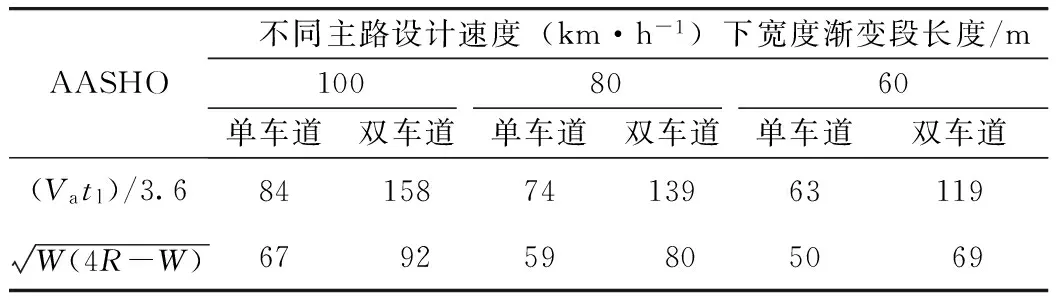
表10　按AASHO方法宽度渐变段长度的计算值

与文献[5]中的规定值比较，单车道计算结果稍大，双车道几乎增大1倍，但规范并未明确双车道的取值。AASHO的计算方法只分析了减速情形，未述及加速情形。对减速情形，车辆移入双车道减速车道的外侧车道，无需连续横移2条车道，可先移入内侧车道再移入外侧车道，整个过程不会增加减速所需长度，宽度渐变段长度采用单车道计算值影响不大。对加速情形，当车辆在双车道加速段外侧车道末端才找到穿插间隙时，会出现车辆连续横移2条车道的状况，如宽度渐变段长度采用单车道计算值则不尽合理。

对双车道加速车道，车辆从外侧车道直接汇入主路的可能性与目标车道的交通流状态有关。完全自由流状态时，目标车道的平均车头时距较大，可穿插间隙较多，车辆连续横移汇入目标车道的情形基本不会出现；当流率逐渐增大时，目标车道的平均车头时距逐渐减小，可穿插间隙随之减少，车辆需要连续横移汇入的可能性随之增大；当稳定流状态时，目标车道的车速及平均车头时距较均衡，可穿插间隙数量较稳定，有一定概率出现车辆连续横移汇入的情形；当饱和流状态时，目标车道的平均车头时距较小，可穿插间隙较少，车辆可连续横移汇入的条件很难具备。当车辆连续横移汇入时，汇入车速应与目标车道车速相近，按连续横移汇入所需车头时距确定目标车道车速，再按此车速确定连续横移的行驶长度，以此作为宽度渐变段长度的控制值是合理的。

车辆横移汇入目标车道(对双车道的外侧车道，可直接横移汇入则表示横越内侧车道时未受到干扰，故不考虑内侧车道的影响)的最小车头时距τd为：

(32)

代入相关数据化简后得：

(33)

满足汇入主路的车头时距的概率P为：

(34)

将式(33)代入式(34)化简后得：

(35)

联立式(28)和式(35)计算不同负荷度下的Vz，τd，P值，列于表11、表12。

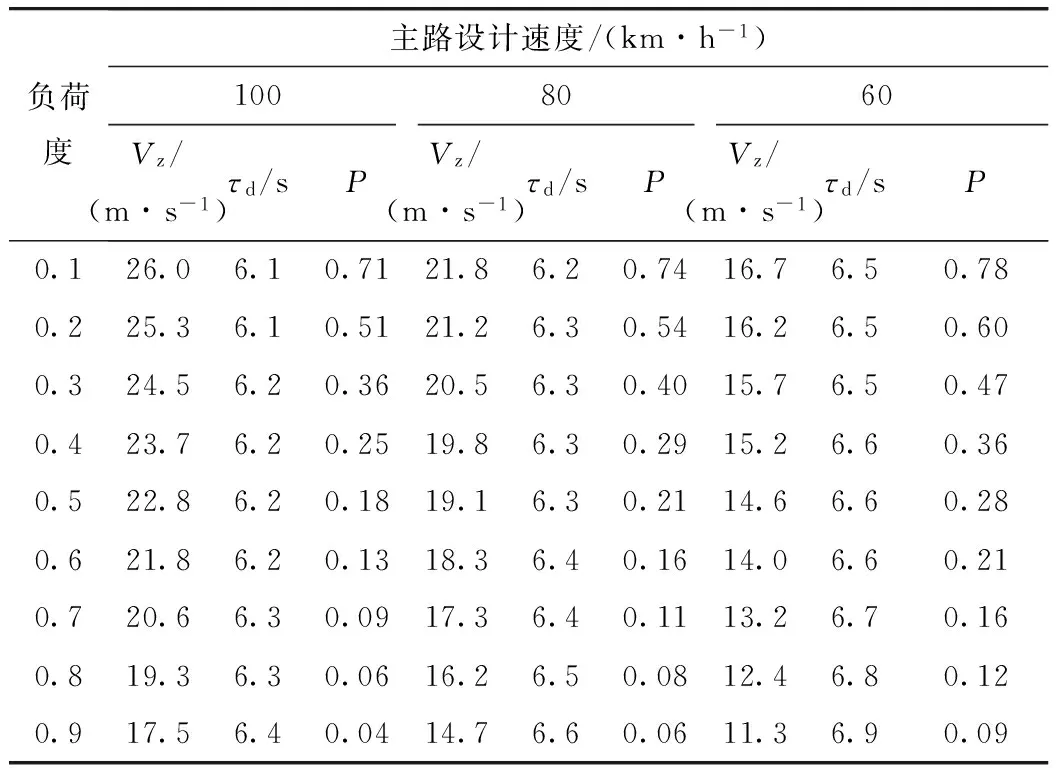
表11　横移1条车道汇入目标车道的Vz, τd, P计算值

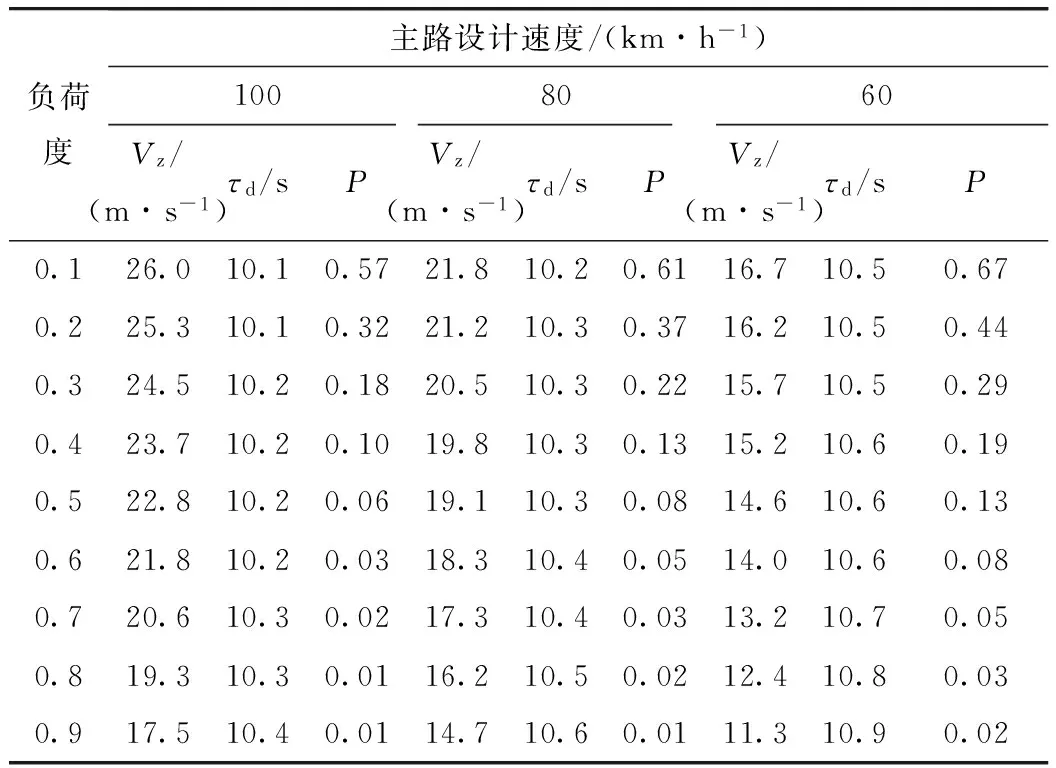
表12　连续横移2条车道汇入目标车道的Vz, τd,P计算值

P值的含义为：在所有可能的车头时距中，满足横移汇入目标车道所需车头时距的概率。对单车道情形，在到达宽度渐变段前车辆已汇入目标车道的概率，即加速车道长度内车头时距不小于τd的概率P′为：

(36)

相应于主路设计速度及目标车道负荷度下的P′计算值参见表11。

主路整体为稳定流状态时，目标车道须处于较低的负荷度，才能容纳从匝道汇入的交通流。按照适宜的匝道设计速度，在连续稳定流状态下、负荷度约为0.8时，匝道的通行能力为1 300～1 400 pcu/h[8]。按主路设计速度及稳定流状态的最大负荷度，确定出目标车道的最大允许流量。匝道交通流量达到通行能力时，要保证连续稳定汇入主路，则目标车道上游的最大允许流量如表13所示。

表13　汇入流量达到匝道通行能力时目标车道上游最大允许流量

根据合流区车辆行驶特征，此时主路内侧车道可认为均达到稳定流下限，该状态下的上游主路流量及负荷度见表14。

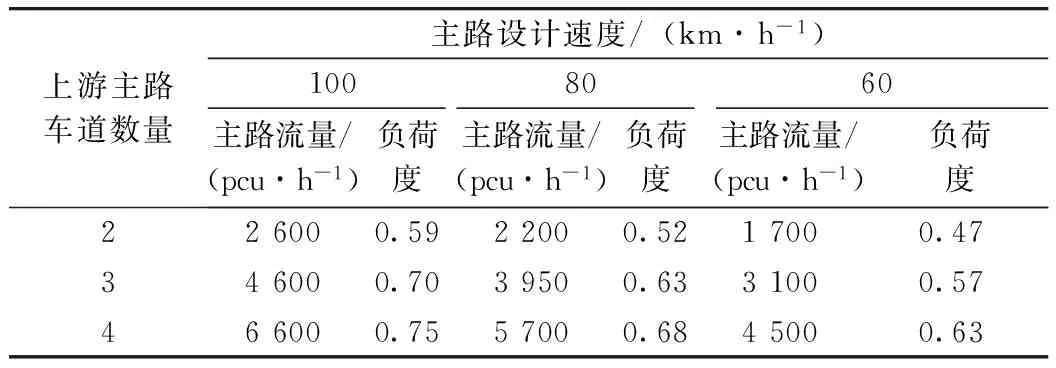
表14　汇入流量达到匝道通行能力时上游主路流量及负荷度

负荷度计算表明上游主路整体处于稳定流服务水平[8]，并有一定余量，故按此状态确定单车道情形下在加速车道长度内可汇入主路的概率(如表15所示)。

表15　车辆在单车道加速车道长度内能汇入目标车道的概率

对单车道加速车道，在到达宽度渐变段前，约有一半机会可汇入目标车道，则在宽度渐变段内汇入目标车道的概率值可取0.50；对双车道加速车道，在加速车道长度内，车辆从外侧车道移至内侧车道后，约有一半机会能汇入目标车道，而单车道宽度渐变段内可提供另外一半机会。因此，车辆连续横移2条车道汇入目标车道，为特殊情况下发生的小概率事件，故概率值可取0.01～0.02。

按可插入间隙概率对应的汇入速度，加速车道的宽度渐变段长度T为:

(37)

式中，Vα为可插入间隙的概率为α时的汇入速度，取概率为α时的目标车道平均车速；tl为汇入车辆横移至目标车道所需时间；α为可插入间隙的概率，单车道取0.50，双车道取0.01～0.02。

按式(37)计算得到的值列于表16。

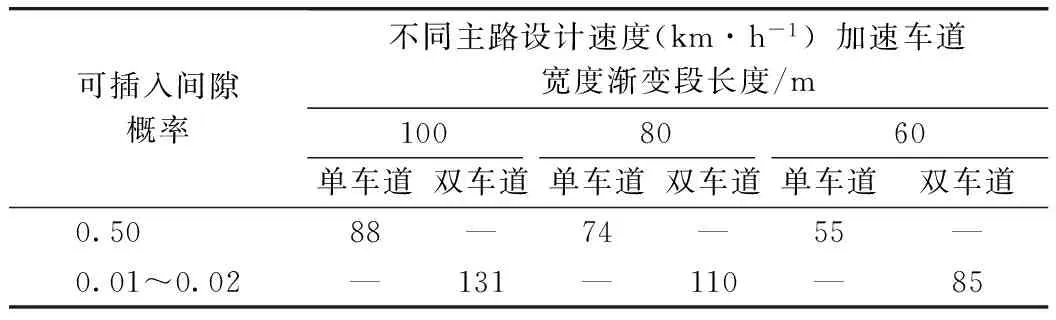
表16　按概率方法加速车道宽度渐变段长度的计算值

对比概率法与AASHO法的计算结果可知，单车道加速车道的数值非常接近，双车道加速车道的计算值明显大于单车道加速车道。综合上述分析，变速车道宽度渐变段长度的最小控制值建议如下。

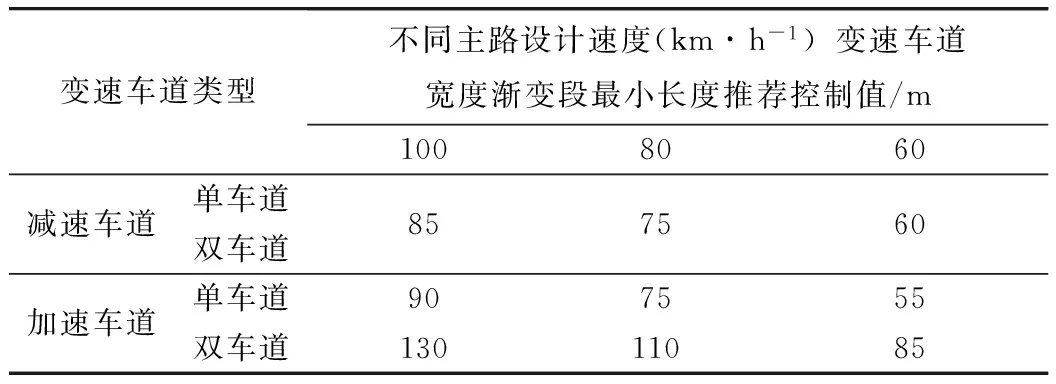
表17　变速车道宽度渐变段最小长度的推荐控制值

4结论

通过分析快速路出入口及匝道的特性，解析了快速路匝道、变速车道控制因素的影响机理。基于运动学原理、交通流理论及概率论等知识建立了匝道、变速车道控制参数的计算模型。运用理论推导、数据计算及与相关研究结果对比等手段，提出了匝道、变速车道控制参数的建议值。

参考文献：

References:

[1]朱胜跃. 城市快速路出入口设置探讨[J]. 城市交通，2004，2 (4)：59-63.

ZHU Sheng-yue. Study on Establishment at the Exit and Entrance of Urban Expressway[J]. Urban Transport of China，2004，2(4)：59-63.

[2]詹琳霞. 城市快速路出入口影响因素研究[D]. 北京：北京工业大学，2008.

ZHAN Lin-xia. Study on Factors affecting Access of Urban Expressway[D]. Beijing：Beijing University of Technology，2008.

[3]汪洋. 城市快速路出入口与公交站点相互关系仿真研究[D]. 北京：北京工业大学，2010.WANG Yang. Study on Relationship between Access of Urban Expressway and Bus Station Based on Micro-simulation[D].Beijing：Beijing University of Technology，2010.

[4]杨晓光，许建，朱彤. 城市快速路公交停靠站与出入口的最小间距研究[J]. 交通信息与安全，2010，28 (2)：1-7,27.

YANG Xiao-guang，XU Jian，ZHU Tong. Minimum Spacing between Bus Station and Entrance/Exit on Urban Expressway[J]. Journal of Transportation Information and Safety，2010，28 (2)：1-7,27.

[5]CJJ129—2009，城市快速路设计规程[S].

CJJ129—2009，Specification for Design of Urban Expressway[S].

[6]JTG B01—2014，公路工程技术标准[S].

JTG B01—2014，Technical Standard of Highway Engineering[S].

[7]JTG D20—2006，公路路线设计规范[S].

JTG D20—2006，Design Specification for Highway Alignment[S].

[8]CJJ37—2012，城市道路工程设计规范[S].

CJJ37—2012，Code for Design of Urban Road Engineering[S].

[9]CJJ193—2012，城市道路路线设计规范[S].

CJJ193—2012，Code for Design of Urban Road Alignment[S].

[10]黄兴安. 公路与城市道路设计手册[M]. 北京：中国建筑工业出版社，2005.

HUANG Xing-an. Manual for Design of Highway and Urban Road[M]. Beijing：China Architecture & Building Press，2005.

[11]戴冀峰，马健宵. 交通工程概论[M]. 北京：人民交通出版社，2006.

DAI Ji-feng，MA Jian-xiao. Generality of Traffic Engineering[M]. Beijing：China Communications Press，2006.

[12]吕集尔，朱留华，郑容森，等. 驾驶员反应时间对行车安全的影响[J]. 交通运输系统工程与信息，2014，14(2)：80-86.

LÜ Ji-er，ZHU Liu-hua，ZHENG Rong-sen, et al. Effects of Driver’s Reaction Time on Safe Driving [J]. Journal of Transportation Systems Engineering and Information Technology，2014，14(2)：80-86.

Study on Control Parameters for Ramp and Speed-change Lane of Urban Expressway

MO Yang

(CCDI(Suzhou)Exploration & Design Consultant Co., Ltd., Suzhou Jiangsu 215123, China)

Abstract：From analyzing the characteristics of entrance/exit, the influencing factors for determining control parameters of ramp and speed-change lane are found out. The mechanisms of effect of ramp design speed and stopping sight distance on the minimum ramp radius as well as the effects of traffic flow rate and ramp design speed on the lengths of speed-change lane and width-transition are resolved. Based on kinematics theory, traffic flow theory and probability theory, the calculation models of control parameters for ramp and speed-change lane are set up. The result of analysis and calculation shows that (1) the design speed of ramp is suitable to be classified according to the patterns and properties of roads on both ends connected by ramp; (2) the minimum curve radius of structure pattern ramp stopping sight distance is greater than that that meets the demands of side-way force coefficient; the calculated values of length for two-lane acceleration lane and width-transition under traffic flow rate affecting are greater than that required in current specifications.

Key words：traffic engineering；control parameter；calculation model；ramp；speed-change lane；lateral clear distance；time headway

收稿日期：2015-02-09

作者简介：莫阳(1969-)，男，上海人，高级工程师. (alex_myoung@126.com)

doi:10.3969/j.issn.1002-0268.2016.05.018

中图分类号：U491.2+23

文献标识码：A

文章编号：1002-0268(2016)05-0111-10